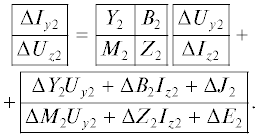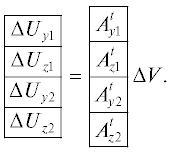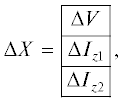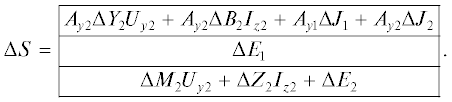Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 493, № 1, стр. 51-56

ВВЕДЕНИЕ

Нулевой уровень электронных схем определяется значением координат рабочих точек всех компонентов схемы при отсутствии управляющих сигналов на входах этой схемы. В зависимости от назначения схемы координаты ее рабочих точек влияют либо только на значения рассеиваемой мощности на компонентах схемы, а также на режимные значения рабочих параметров компонентов в этих точках, либо, кроме того, определяют приведенный к входу нулевой уровень, являющийся основной характеристикой широкого класса электронных схем, к которым относятся операционные усилители, стабилизаторы и т.д. [1, 2]. Анализ нестабильности нулевого уровня электронных схем является важнейшим этапом проектирования современной электронной аппаратуры [3, 4]. Недостаточное внимание к этой проблеме может привести к изменению основных характеристик проектируемой электронной схемы или даже к необратимому нарушению их функционирования вследствие превышения допустимой мощности, рассеиваемой на некоторых компонентах. Поэтому современные системы автоматизации схемотехнического проектирования должны иметь в своем составе инструментальные средства для решения такой задачи. При этом в процессе расчета нестабильности нулевого уровня электронных схем необходимо учитывать, как влияние на параметры компонентов внешних воздействий (изменение температуры, влажности, давления, радиации и т.д.), так и технологический разброс параметров при серийном изготовлении компонентов.

Возможны два подхода к выбору метода построения математического описания подсистемы для автоматизации расчета нестабильности нулевого уровня электронных схем. Первый подход предусматривает реализацию расчета вектора базисных переменных стационарного режима нелинейной электронной схемы путем схемотехнической интерпретации метода Ньютона–Рафсона с запоминанием результатов линеаризации схемы на последней итерации [5, 6]. Эти результаты затем используются для расчета векторной или скалярной чувствительности переменных моделируемой схемы к вариации параметров компонентов путем построения соответствующих моделирующих схем. Такая задача решается либо путем дифференцирования уравнений нелинейной схемы, либо методом присоединенной схемы, которая строится на основании теоремы Теллегена [7, 8]. Решение задачи расчета нестабильности нулевого уровня электронных схем при таком подходе неизбежно связано с необходимостью выполнения большого объема вычислительных операций, требующих для своей реализации большого объема оперативной памяти и значительного времени для полного решения задачи расчета стационарного режима нелинейной схемы с последующим расчетом чувствительности ее переменных.

Второй подход к построению математического описания подсистемы для автоматизации расчета нестабильности нулевого уровня электронных схем учитывает то обстоятельство, что при проектировании электронных схем часто встречаются ситуации, когда координаты рабочих точек всех компонентов схемы известны и требуется определить лишь отклонения значений этих координат при вариации параметров компонентов схемы и внешних воздействий [9]. При этом появляется возможность исключить необходимость расчета чувствительности нелинейной схемы к вариации ее параметров и перейти к рассмотрению математического описания, в качестве переменных которого выступают отклонения переменных от начального стационарного значения. При таком подходе к реализации математического описания резко уменьшается объем вычислительных операций и снижается время расчета нестабильности нулевого уровня, что особенно важно при решении оптимизационных задач проектирования электронных схем, требующих многократного расчета схемы для нахождения оптимального значения ее параметров.

В работе рассматривается методика построения математического описания подсистемы автоматизации расчета нестабильности нулевого уровня электронных схем, отличительной особенностью которой является использование только линеаризованных уравнений, на основании которых возможен расчет нестабильности нулевого уровня электронных схем при вариации параметров компонентов как вследствие внешних воздействий, так и вследствие технологического разброса при серийном изготовлении компонентов.

КОМПОНЕНТНЫЕ УРАВНЕНИЯ ЭЛЕКТРОННЫХ СХЕМ

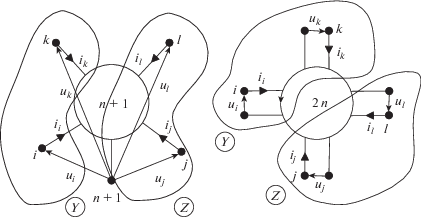
Компоненты электронных схем можно представить в виде многополюсников типа (n + 1) и 2n-полюсников, структура которых приведена на рис. 1.

Для каждого многополюсника зависимость между двумя переменными может быть описана уравнениями $p = f( \ldots ,\;q,\; \ldots )$, которые в явной форме определяют для каждого полюса одну из полюсных переменных, при этом переменная p в общем случае может быть как токовой, так и потенциальной переменной. В зависимости от характера этой переменной все полюсы многополюсников могут быть разделены на две группы [10]. Первой группой, которую обычно называют группой y-полюсов, являются полюсы, для которых зависимая переменная p является переменной токового типа, а второй группой, обычно называемой группой z-полюсов, являются полюсы, для которых зависимая переменная p является переменной потенциального типа.

Учитывая, что характеристики компонентов зависят от внешних воздействий ε_m (изменение температуры, влажность, давление, радиация и т.д.) уравнения y-полюсов и z-полюсов нелинейных многополюсников можно записать в следующем виде:

Выполняя разложение уравнений y-полюсов и z-полюсов нелинейных многополюсников в ряд Тейлора в окрестности рабочих точек с координатами $i_{{i1}}^{0}$, $u_{{k1}}^{0}$, $i_{{l1}}^{0}$, $u_{{j1}}^{0}$ и внешних воздействий $\varepsilon _{m}^{0}$ и ограничиваясь в этом разложении членами первого порядка малости, получим систему линеаризованных уравнений

Вводя обозначения

и переходя к отклонениям переменных и внешних воздействий от начальных значений можно представить уравнения линеаризованного многополюсника (3) и (4) в виде где

Уравнения (5) и (6) определяют отклонения координат рабочих точек нелинейных компонентов при изменении внешних воздействий, при этом значения приращений автономных параметров под воздействием внешних возмущений ε_m определяются выражениями (7). Графически приращения автономных параметров можно интерпретировать как сдвиг рабочей точки характеристик компонента вдоль вертикальной оси при изменении некоторого внешнего воздействия Δε_m.

Введем векторы $\Delta {{I}_{{y1}}}$, $\Delta {{I}_{{z1}}}$, $\Delta {{U}_{{y1}}}$, $\Delta {{U}_{{z1}}}$ для приращений переменных $\Delta {{i}_{{y1}}}$, $\Delta {{i}_{{z1}}}$, $\Delta {{u}_{{y1}}}$, $\Delta {{u}_{{z1}}}$, векторы $\Delta {{J}_{1}}$, $\Delta {{E}_{1}}$ для приращений автономных параметров $\Delta {{j}_{{i1}}}$, $\Delta {{e}_{{j1}}}$ и матрицы $Y_{1}^{0}$, $B_{1}^{0}$, $M_{1}^{0}$, $Z_{1}^{0}$ для значений неавтономных параметров $y_{{ik1}}^{0}$, $\beta _{{il1}}^{0}$, $\mu _{{jk1}}^{0}$, $z_{{jl1}}^{0}$. Тогда можно записать линеаризованные уравнения (5) и (6) для y-полюсов и z-полюсов в матричной форме:

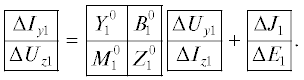
Объединяя уравнения (8) и (9), получим матричное уравнение для отклонений переменных линеаризованных в рабочих точках нелинейных многополюсников схемы

Уравнения линейных многополюсников имеют вид

где ${{y}_{{ik2}}}$, ${{\beta }_{{il2}}}$, ${{\mu }_{{jk2}}}$, ${{z}_{{jl2}}}$ – неавтономные параметры, ${{j}_{{i2}}}$, ${{e}_{{j2}}}$ – автономные параметры (задающие источники) линейных многополюсников, которые зависят от внешних воздействий ε_m.

Выполняя дифференцирование уравнений (11) и (12) с учетом зависимостей неавтономных и автономных параметров линейных многополюсников от внешних воздействий ε_m и переходя к конечным приращениям, получим уравнения

где приращения неавтономных параметров при изменении внешних воздействий и приращения для автономных параметров (задающих источников) при изменении внешних воздействий

Введем для описания линейных многополюсников матрицы Y₂, B₂, M₂, Z₂, определяющие значения неавтономных параметров $y_{{ik2}}^{{}}$, $\beta _{{il2}}^{{}}$, $\mu _{{jk2}}^{{}}$, $z_{{jl2}}^{{}}$, векторы $\Delta {{I}_{{y2}}}$, $\Delta {{I}_{{z2}}}$, $\Delta {{U}_{{y2}}}$, $\Delta {{U}_{{z2}}}$ для приращений переменных $\Delta {{i}_{{y2}}}$, $\Delta {{i}_{{z2}}}$, $\Delta {{u}_{{y2}}}$, $\Delta {{u}_{{z2}}}$ линейных многополюсников, матрицы $\Delta {{Y}_{2}}$, $\Delta {{B}_{2}}$, $\Delta {{M}_{2}}$, $\Delta {{Z}_{2}}$ для приращений неавтономных параметров $\Delta {{y}_{{ik2}}}$, $\Delta {{\beta }_{{il2}}}$, $\Delta {{\mu }_{{jk2}}}$, $\Delta {{z}_{{jl2}}}$, векторы $\Delta {{J}_{2}}$, $\Delta {{E}_{2}}$ для приращений автономных параметров $\Delta {{j}_{{i2}}}$, $\Delta {{e}_{{j2}}}$, векторы U_y, I_z для координат потенциальных и токовых переменных ${{u}_{{k2}}}$, ${{i}_{{l2}}}$ многополюсника в исходной рабочей точке. Тогда можно записать уравнения (13) и (14) линейных многополюсников для y-полюсов и z-полюсов в матричной форме:

Объединяя уравнения (17) и (18), получим матричное уравнение линейных многополюсников схемы для отклонений переменных и внешних воздействий

Влияние внешних воздействий ε_m на неавтономные параметры ${{y}_{{ik2}}}$, ${{\beta }_{{il2}}}$, ${{\mu }_{{jk2}}}$, ${{z}_{{jl2}}}$ в уравнении (19) линейных многополюсников определяется матрицами ΔY₂, ΔB₂, ΔM₂, ΔZ₂. Составляющие этих матриц задаются приращениями неавтономных параметров при изменении внешних воздействий $\Delta {{y}_{{ik2}}}$, $\Delta {{\beta }_{{il2}}}$, $\Delta {{\mu }_{{jk2}}}$, $\Delta {{z}_{{jl2}}}$, которые вычисляются для конкретного типа внешнего воздействия (изменение температуры, влажность, давление, радиация и т.д.) согласно выражениям (15). В некоторых случаях, например при оценке влияния технологического разброса при серийном изготовлении компонентов, значения $\Delta {{y}_{{ik2}}}$, $\Delta {{\beta }_{{il2}}}$, $\Delta {{\mu }_{{jk2}}}$, $\Delta {{z}_{{jl2}}}$ задаются исходя из имеющейся информации о технологическом разбросе параметров [11, 12]. Аналогично влияние внешних воздействий ε_m на автономные параметры (задающие источники) в уравнении (19) определяется векторами ΔJ₂, ΔE₂. Составляющие этих векторов задаются приращениями автономных параметров при изменении внешних воздействий $\Delta {{j}_{{i2}}}$, $\Delta {{e}_{{j2}}}$, которые могут быть вычислены согласно выражениям (16) или заданы на основании известной информации о нестабильности источников питания схемы.

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПОДСИСТЕМЫ АВТОМАТИЗАЦИИ РАСЧЕТА НЕСТАБИЛЬНОСТИ НУЛЕВОГО УРОВНЯ ЭЛЕКТРОННЫХ СХЕМ

Для построения математического описания подсистемы автоматизации расчета нестабильности нулевого уровня электронных схем необходимо дополнить компонентные уравнения нелинейных и линейных многополюсников (10) и (19) топологическими уравнениями, которые описывают структуру схемных связей многополюсных компонентов электронной схемы. Выбор типа топологических уравнений зависит от выбранного способа формирования координатного базиса. Наиболее просто задача решается путем построения топологических уравнений на основе матрицы инциденции с последующим объединением компонентных уравнений с построенными топологическими уравнениями. Однако в этом случае в число переменных координатного базиса входят все переменные, отображенные в компонентных уравнениях, а также узловые потенциалы схемы, и решение уравнений связано с обработкой матриц весьма значительного размера. Другим крайним случаем является построение топологических уравнений на основе рассмотрения совокупности главных сечений и главных контуров полюсного графа, в котором выбрано некоторое дерево [13–15]. Такой подход к формированию уравнений позволяет использовать вырождение координат с соответствующим снижением числа составляющих координатного базиса до минимально возможного размера. Однако построение матриц главных контуров и главных сечений на основе выбора и рассмотрения дерева полюсного графа схемы требует использования достаточного сложного программного обеспечения, что связано с большими временными затратами как при его разработке, так и при выполнении для решения задач моделирования. Компромиссным вариантом решения задачи является построение топологического описания схемы на основе матрицы инциденции с последующим переходом к расширенному координатному базису узловых потенциалов путем исключения из его составляющих всех переменных, кроме узловых потенциалов и токовых переменных z-полюсов.

Топологические уравнения для токовых переменных при расчете нестабильности нулевого уровня электронных схем можно записать в виде

где ${{A}_{{y1}}}$, ${{A}_{{z1}}}$, ${{A}_{{y2}}}$, ${{A}_{{z2}}}$ – блочные матрицы общей матрицы инциденций

Топологические уравнения для потенциальных переменных в координатной форме имеют вид

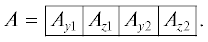
Объединяя топологические уравнения с компонентными уравнениями (10) и (19) и исключая из них векторы $\Delta {{I}_{{y1}}}$, $\Delta {{I}_{{y2}}}$, $\Delta {{U}_{{y1}}}$, $\Delta {{U}_{{y2}}}$, $\Delta {{U}_{{z1}}}$, $\Delta {{U}_{{z2}}}$, получим уравнения схемы в расширенном базисе узловых потенциалов:

где

Уравнение (20) построено в расширенном базисе узловых потенциалов и позволяет реализовать математическое описание моделируемой схемы для расчета нестабильности ее нулевого уровня при воздействии внешних возмущений с учетом сдвига рабочих точек характеристик нелинейных компонентов вдоль вертикальной оси при изменении некоторого внешнего воздействия Δε_m и с учетом вариации параметров линейных многополюсных компонентов под влиянием этого внешнего воздействия.

ЗАКЛЮЧЕНИЕ

В работе предлагается методика расчета нестабильности нулевого уровня электронных схем, основанная на использовании математического описания линеаризованной схемы для отклонений переменных от начального стационарного значения под влиянием внешних воздействий, а также вследствие технологического разброса параметров компонентов при их изготовлении. При этом исключается необходимость многократного расчета нелинейной схемы, требующего выполнения большого количества итерационных процедур и резко уменьшается объем вычислительных операций, что имеет большое значение при решении оптимизационных задач проектирования электронных схем, в процессе решения которых требуется выполнение многократного расчета схемы. Математическое описание предлагаемой методики расчета нестабильности нулевого уровня электронных схем основано на использовании расширенного координатного базиса, что позволяет минимизировать число его составляющих и обеспечивает возможность описания электронных схем с произвольными смешанными типами компонентов.