1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 493, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 493, № 1, стр. 57-61

ПРЕДЕЛЫ ДЕТАЛИЗАЦИИ ОПИСАНИЯ ЗАДАЧ МЕХАНИКИ СПЛОШНЫХ СРЕД И ЧИСЛЕННЫЙ АЛГОРИТМ ДЛЯ МОДЕЛИРОВАНИЯ ТЕЧЕНИЙ ВЯЗКОГО ГАЗА

А. Е. Луцкий 1, *, академик РАН Б. Н. Четверушкин 1

1 Федеральный исследовательский центр Институт прикладной математики им. М.В. Келдыша Российской академии наук
Москва, Россия

* E-mail: allutsky@yandex.ru

Поступила в редакцию 26.05.2020
После доработки 26.05.2020
Принята к публикации 28.05.2020

Полный текст (PDF)

Аннотация

Рассматривается математическая модель для описания течений вязкого газа, учитывающая ограничение временных масштабов характерным временем между столкновениями молекул. Данный подход является вариантом квазигазодинамической системы уравнений, основанной на связи между кинетическим и макроскопическим описаниями движения сплошной среды. На основе представленной модели построен численный алгоритм для моделирования течений вязкого сжимаемого газа. В качестве примера использования алгоритма рассматриваются некоторые особенности обтекания затупленных тел неоднородным потоком.

Ключевые слова: квазигазодинамическая система уравнений, метод конечного объема, явная разностная схема, сверхзвуковое течение

ВВЕДЕНИЕ

Вывод системы квазигазодинамических уравнений (КГД) из уравнений Больцмана аналогичен процедуре получения уравнений газовой динамики [1–3]. При этом сама КГД-система для моделирования течения вязкого теплопроводного газа отличается от аналогичной системы уравнений Навье–Стокса на члены второго порядка малости по числу Кнудсена O(Kn2).

Вывод КГД-системы из кинетической модели в явном виде опирается на тот факт, что вблизи равновесия одночастичная функция распределения слабо меняется на расстоянии длины свободного пробега $l$ или за время порядка характерного времени между столкновениями молекул $\tau $. Предположим, что на момент времени $t = {{t}^{j}}$ одночастичная функция распределения молекул имеет локально-максвелловский вид:

(1)
$f({{t}^{j}},~x,\xi ) = {{f}_{0}} = \frac{{\rho (t,{\mathbf{x}})}}{{{{{\left( {2\pi RT(t,x)} \right)}}^{{3/2}}}}}l\frac{{ - {{{\left( {{{\xi }_{i}} - {{u}_{i}}(t,x)} \right)}}^{2}}}}{{2RT}},$
здесь $R$ – газовая постоянная, $\xi $ – вектор скорости молекул.

Предположим, что в течение времени ${{t}^{{j + 1}}}\, - \,{{t}^{j}}{\kern 1pt} $ = τ молекулы газа совершают бесстолкновительный разлет. В момент времени $t = {{t}^{{j + 1}}}$ происходит мгновенный процесс столкновения молекул и функция распределения вновь становится локально-максвелловской. Связь между значением функции распределения до максвеллизации на момент времени ${{t}^{{j + 1}}}$ и значением локально-максвелловской функции на момент времени ${{t}^{j}}$ выражается соотношением

(2)
$f({{t}^{{j + 1}}},{\mathbf{x}},\xi ) = {{f}_{0}}({{t}^{j}},{\mathbf{x}} - \xi ,\tau ,\xi ).$

Разложим правую часть (2) в ряд Тейлора с точностью до членов третьего порядка малости по величине $\left| \xi \right|\tau $:

(3)
$f({{t}^{{j + 1}}},{\mathbf{x}},\xi ) - {{f}_{0}}({{t}^{j}},{\mathbf{x}},\xi ) = - \tau {{\xi }_{i}}\frac{{\partial {{f}_{0}}}}{{\partial {{x}_{i}}}} + \frac{\partial }{{\partial {{x}_{k}}}}\frac{\tau }{2}{{\xi }_{i}}{{\xi }_{k}}\frac{{\partial {{f}_{0}}}}{{\partial {{x}_{i}}}}.$

Умножим левую и правую части (3) на сумматорный инвариант m и проинтегрируем по скоростям молекул:

(4)
${{\rho }^{{j + 1}}} - {{\rho }^{j}} = - \tau \operatorname{div} \rho {\mathbf{u}} + \frac{\partial }{{\partial {{x}_{k}}}}\frac{\tau }{2}\frac{\partial }{{\partial {{x}_{i}}}}(\rho {{u}_{i}}{{u}_{k}} + {{\delta }_{{ik}}}p).$

Разлагая левую часть (4) в ряд Тейлора, окончательно придем к уравнению

(5)
$\frac{{\partial \rho }}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho }}{{\partial {{t}^{2}}}} + \operatorname{div} \rho {\mathbf{u}} = \frac{\partial }{{\partial {{x}_{k}}}}\frac{\tau }{2}\frac{\partial }{{\partial {{x}_{i}}}}(\rho {{u}_{i}}{{u}_{k}} + {{\delta }_{{ik}}}p).$

Это уравнение отличается от классического уравнения неразрывности на совокупность членов

(6)
$\frac{\tau }{2}\frac{{{{\partial }^{2}}\rho }}{{\partial {{t}^{2}}}} - \frac{\partial }{{\partial {{x}_{k}}}}\frac{\tau }{2}\frac{\partial }{{\partial {{x}_{i}}}}(\rho {{u}_{i}}{{u}_{k}} + {{\delta }_{{ik}}}p),$
которые в сумме составляют величину порядка $O({{\operatorname{Kn} }^{2}})$ [1, 2].

Система КГД-уравнений может быть получена также на основе феноменологических соображений.

Рассмотрим изменения массы в конечном объеме Ω за время ${\Delta }t = {{t}^{{j + 1}}} - {{t}^{j}}$

(7)
${{M}^{{j + 1}}} - {{M}^{j}} = \mathop \smallint \limits_\Omega {{\rho }^{{j + 1}}}dx - \mathop \smallint \limits_\Omega {{\rho }^{j}}dx = - \mathop \smallint \limits_{{{t}^{j}}}^{{{t}^{{j + 1}}}} \oint\limits_S {\rho uds,} $
где $S$ – поверхность, ограничивающая объем ${\Omega }$, $M$ – масса объема Ω.

Рассмотрим конечный временной интервал, на котором происходит изменение массы объема $\Omega $, ${\Delta }t = {{t}^{{j + 1}}} - {{t}^{j}} = \tau $.

Представим импульс $\rho u$ на отрезке $t \in [{{t}^{j}},{{t}^{j}}{\kern 1pt} + {\kern 1pt} \tau ]$ в виде

(8)
$\rho u(t) = \rho {{u}^{j}} + \tau \frac{{\partial \rho {{u}^{j}}}}{{\partial t}} + O(\Delta {{t}^{2}}).$

Подставим (8) в правую часть (7), проинтегрируем по времени на отрезке $[{{t}^{j}}{\kern 1pt} ,~{{t}^{{j + 1}}}]$ и воспользуемся теоремой Гаусса–Остроградского:

(9)
${{\rho }^{{j + 1}}} - {{\rho }^{j}} = - \tau \operatorname{div} \left( {\rho {{u}^{j}} + \frac{\tau }{2}\frac{{\partial \rho {{u}^{j}}}}{{\partial t}}} \right) + O(\Delta {{t}^{2}}).$

Левую часть выражения (9) представим в виде

(10)
${{\rho }^{{j + 1}}} - {{\rho }^{j}} = \tau \frac{{\partial {{\rho }^{j}}}}{{\partial t}} + \frac{{{{\tau }^{2}}}}{2}\frac{{{{\partial }^{2}}{{\rho }^{j}}}}{{\partial {{t}^{2}}}} + O({{\tau }^{2}}),$
а для нахождения $\left( {\frac{{\partial \rho u}}{{\partial t}}} \right)$ воспользуемся выражением
(11)
$\frac{{\partial \rho {{u}_{i}}}}{{\partial t}} = - \frac{{\partial \left( {\rho {{u}_{i}}{{u}_{k}} + {{\delta }_{{ik}}}p} \right)}}{{\partial {{x}_{k}}}},$
которое выполняется точно для уравнения, описывающего изменение импульса в идеальном газе. В неидеальном газе это выражение выполняется с точностью до членов, описывающих вязкое напряжение, т.е. O(τ). Комбинируя (9)–(11), окончательно получим уравнение
(12)
$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}\rho }}{{\partial {{t}^{2}}}} + \operatorname{div} (\rho {\mathbf{u}}) = \\ = \frac{\partial }{{\partial {{x}_{i}}}}\frac{\tau }{2}\frac{\partial }{{\partial {{x}_{k}}}}(\rho {{u}_{i}}{{u}_{k}} + {{\delta }_{{ik}}}p), \\ \end{gathered} $
которое в точности совпадает с уравнением (5), полученным на основе дискретной кинетической модели.

Введение ограничения снизу на допустимый интервал по времени приводит как в рамках дискретной кинетической модели, так и макроскопического описания к появлению дополнительных членов в уравнении неразрывности. Аналогичные члены появляются при выводе уравнений сохранения импульса и энергии.

Недостатком традиционной КГД-системы является ее более громоздкий вид по сравнению с уравнениями Навье–Стокса. Нестандартный вид членов, входящих в КГД-систему, вызывал определенные трудности при использовании алгоритмов, ранее разработанных для решения уравнений Навье–Стокса. В работе [4] на основе оценки по порядку величин входящих в нее членов был предложен “компактный” вариант, представленный в разделе 1.

1. ЧИСЛЕННЫЙ АЛГОРИТМ

Система гиперболических КГД-уравнений в компактной форме имеет вид

(13)
$\frac{{\partial Q}}{{\partial t}} + \frac{\tau }{2}\frac{{{{\partial }^{2}}Q}}{{\partial {{t}^{2}}}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} = 0~,$
$F = {{F}^{i}} + {{F}^{v}},\quad G = {{G}^{i}} + {{G}^{v}},$
$Q = \left( {\begin{array}{*{20}{c}} \rho \\ {\rho u} \\ {\rho v} \\ E \end{array}} \right),\quad {{F}^{i}} = \left( {\begin{array}{*{20}{c}} {\rho (u - {{w}_{1}})} \\ {\rho u(u - {{w}_{1}}) + p} \\ {\rho u(v - {{w}_{2}})} \\ {(E + p)(u - {{w}_{1}})} \end{array}} \right),$
${{F}^{v}} = \left( {\begin{array}{*{20}{c}} 0 \\ { - {{\sigma }_{{xx}}}} \\ { - {{\sigma }_{{xy}}}} \\ { - u{{\sigma }_{{xx}}} - v{{\sigma }_{{xy}}} - {{q}_{x}}} \end{array}} \right),$
${{G}^{i}} = \left( {\begin{array}{*{20}{c}} {\rho (v - {{w}_{2}})} \\ {\rho v(u - {{w}_{1}})} \\ {\rho v(v - {{w}_{2}}) + p} \\ {(E + p)(v - {{w}_{2}})} \end{array}} \right),\quad {{G}^{v}} = \left( {\begin{array}{*{20}{c}} 0 \\ { - {{\sigma }_{{xy}}}} \\ { - {{\sigma }_{{yy}}}} \\ { - u{{\sigma }_{{xy}}} - v{{\sigma }_{{yy}}} - {{q}_{y}}} \end{array}} \right),$
$\begin{gathered} {{w}_{1}} = \frac{\tau }{{2\rho }}\left( {\frac{\partial }{{\partial x}}(\rho {{u}^{2}} + p) + \frac{\partial }{{\partial y}}\left( {\rho uv} \right)} \right), \\ {{w}_{2}} = \frac{\tau }{{2\rho }}\left( {\frac{\partial }{{\partial x}}\left( {\rho uv} \right) + \frac{\partial }{{\partial y}}(\rho {{v}^{2}} + p)} \right), \\ \end{gathered} $
${{\sigma }_{{xx}}} = \frac{2}{3}\mu \left( {2\frac{{\partial u}}{{\partial x}} - \frac{{\partial v}}{{\partial y}}} \right),\quad {{\sigma }_{{xy}}} = {{\sigma }_{{yx}}} = \mu \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right),$
${{\sigma }_{{yy}}} = \frac{2}{3}\mu \left( {2\frac{{\partial v}}{{\partial y}} - \frac{{\partial u}}{{\partial x}}} \right),\quad {{q}_{x}} = \kappa \frac{{\partial T}}{{\partial x}},\quad {{q}_{y}} = \kappa \frac{{\partial T}}{{\partial y}}.$

Здесь $t$ – время; $x,\;y$ – пространственные координаты; $\rho $ – плотность; $(u,v)$ – вектор скорости; $E$ – полная энергия; $p$ – давление; (w1, w2) – вектор дополнительного переноса массы; $({{q}_{x}},{{q}_{y}})$ – вектор теплового потока, $T$ – температура, $\kappa $ – коэффициент теплопроводности; $\sigma $ – тензор вязких напряжений в уравнениях Навье–Стокса, µ = = µM + µT – эффективная вязкость.

Рассматриваемое в разделе 2 течение является турбулентным, поэтому при построении численного алгоритма используется гиперболическая КГД-система, осредненная по времени. Такой подход вполне аналогичен переходу от уравнений Навье–Стокса к уравнениям Рейнольдса. В сочетании с КГД-системой уравнений ранее он использовался в работе [5]. Турбулентная вязкость µT определяется на основе современного варианта модели Спеларта–Аллмараса [6].

Для численного интегрирования системы (13) используется явная разностная схема

$\begin{gathered} \Omega \frac{{Q_{{ij}}^{{n + 1}} - Q_{{ij}}^{n}}}{{\Delta t}} + \Omega \frac{{\tau {\kern 1pt} *}}{2}\frac{{Q_{{ij}}^{{n + 1}} - 2Q_{{ij}}^{n} + Q_{{ij}}^{{n - 1}}}}{{\Delta {{t}^{2}}}} + \\ \, + \sum\limits_{k = 1}^4 {{{{\left( {F{{n}_{x}} + G{{n}_{y}}} \right)}}_{k}}} = 0. \\ \end{gathered} $

Здесь $F,G$ – векторы потоков, определяемые соотношениями (1), $\left( {{{n}_{x}},{{n}_{y}}} \right)$ – вектор нормали, $\Omega $ – площадь ячейки. Чтобы получить значения консервативных переменных $Q_{{ij}}^{{n + 1}}$ на следующем слое по времени, необходимо по известным величинам $Q_{{ij}}^{n},\;Q_{{ij}}^{{n - 1}}$ вычислить на всех ребрах численные потоки ${{\left( {F{{n}_{x}} + G{{n}_{y}}} \right)}_{k}}$. Для реконструкции значений переменных на гранях используется схема типа MUSCL, обеспечивающая второй порядок аппроксимации по пространству. Газодинамические величины на ребре ячейки определяются на основе точного решения задачи Римана.

2. ОСОБЕННОСТИ ОБТЕКАНИЯ ЗАТУПЛЕННЫХ ТЕЛ НЕОДНОРОДНЫМ ПОТОКОМ

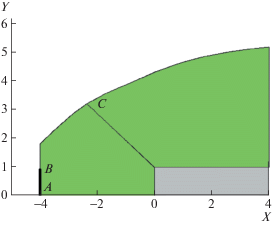
Рассматривается сверхзвуковое осесимметричное обтекание затупленного тела – цилиндра (рис. 1) неоднородным потоком. На участке AB (r – длина отрезка AB) входной границы задаются параметры сверхзвуковой струи, на участке BC – параметры невозмущенного сверхзвукового потока. Данная задача моделирует в упрощенной постановке влияние струи двигателя верхней ступени ракеты-носителя на обтекание нижней ступени в процессе их разделения [7].

Рис. 1.

Постановка задачи. Расчетная область.

Представленные ниже результаты получены на сетке, состоящей из двух блоков с общим числом ячеек 350 208 (400 ячеек вдоль торца цилиндра). Статическое давление в струе равно статическому давлению набегающего потока (принято за 1), полное давление и давление торможения за прямым скачком (давление Пито) в струе существенно ниже, чем в набегающем потоке, статическая температура и температура торможения – существенно выше. Число Рейнольдса по отношению к радиусу цилиндра Re = 1.2 × 106.

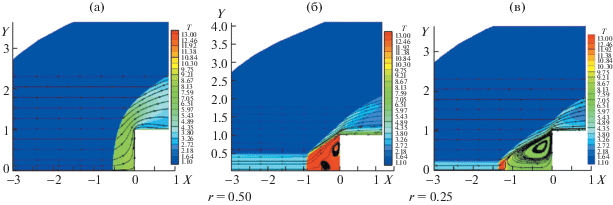
Характерные режимы течения показаны на рис. 2: а – обтекание невозмущенным потоком, б – струя радиусом r = 0.5 – режим 1, в – струя радиусом r = 0.25 – режим 2.

Рис. 2.

Характерные режимы течения. Распределение температуры и линии тока.

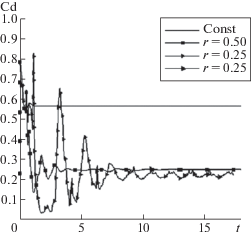
Вариант (а) представляет классический режим безотрывного обтекания с отошедшей головной ударной волной. В силу низких значений давления Пито при наличии струи такой режим реализоваться не может. В этом случае поперек струи формируется скачок, а за ним коническая область перед торцом цилиндра. Для режима 1 формируется практически стационарное решение с небольшими вихревыми структурами. Коническая область заполнена горячим газом с температурой, близкой к температуре торможения струи. Напротив, для режима 2 (r = 0.25) реализуется нестационарное пульсирующее решение, близкое к периодическому (см. рис. 3). Значительная часть конической области заполнена относительно холодным газом с температурой, близкой к температуре торможения невозмущенного потока. Именно в этой области возникает отрыв и формируются нестационарные вихревые структуры большого размера.

Рис. 3.

Зависимость от времени коэффициентов сопротивления.

При обтекании невозмущенным потоком давление на торце цилиндра вблизи оси симметрии близко к теоретическому значению давления Пито в набегающем потоке. Для вариантов (б), (в) давление значительно ниже и вблизи оси симметрии практически совпадает с теоретическим значением давления Пито в струе. Наибольшая температура на торце реализуется для варианта (б) и соответствует температуре торможения в струе. Для вариантов (а) и (в) температура на торце значительно ниже и близка к температуре торможения в невозмущенном потоке.

Отмеченные отличия между режимами обусловлены особенностями формирования и эволюции течения. На начальном этапе при взаимодействии струи с формирующейся головной ударной волной возникает вихревая структура. В случае режима 1 этот вихрь располагается близко к угловой точке цилиндра и постепенно выносится из конической области перед торцом. Размеры “холодной” области уменьшаются. В режиме 2 вихрь начинает формироваться ближе к оси симметрии вследствие меньшего радиуса струи. Далее центр вихря несколько поднимается, но не выходит из конической области перед торцом. В процессе эволюции размеры вихревой области несколько раз увеличиваются примерно в 2 раза по сравнению с состоянием, изображенном на рис. 2. Давление на боковой поверхности цилиндра для всех вариантов по мере движения вниз по потоку выравнивается и практически выходит на уровень статического давления невозмущенного потока. Для варианта r = 0.50 вдоль всей поверхности цилиндра располагается область горячего газа струи. Указанный факт имеет большое практическое значение для проектирования теплозащитных покрытий аэрокосмических аппаратов.

Схожие явления были обнаружены ранее в работе [8], но для существенно меньших чисел Маха набегающего потока (М = 1.89–3.45). Детальное выявление специфики рассматриваемого гиперзвукового течения явится предметом дальнейших исследований.

ЗАКЛЮЧЕНИЕ

В работе рассмотрена гиперболическая система КГД-уравнений в компактной форме. Вывод системы опирается на учет ограничений степени детализации по пространству и времени описания физических процессов. Численные алгоритмы, первоначально предназначенные для уравнений Навье–Стокса, легко обобщаются на случай КГД-уравнений. С помощью одного из таких алгоритмов проведены расчеты гиперзвукового обтекания неравномерным потоком затупленного тела. Показано наличие нескольких режимов течения, различающихся размерами и расположением областей отрыва, температурой на поверхности тела и другими параметрами.

Список литературы

  1. Chetverushkin B.N. Kinetic Schemes and Quasi-Gas Dynamic System of Equations. CIMNE. Barcelona, 2008, 298 p.

  2. Chapman S., Cowling T.G. The Mathematical Theory of Non-Uniform Gases. 3rd edition. Cambridge etc.: Cambridge University Press, 1990.

  3. Cercignani C. Mathematical Methods in Kinetic Theory. Springer US, 1969.

  4. Четверушкин Б.Н., Савельев А.В., Савельев В.И. Квазигазодинамическая модель для описания магнитогазодинамических явлений // ЖВМиМФ. 2018. Т. 58. № 8. С. 1384–1394.

  5. Ивахненко И.А., Поляков С.В., Четверушкин Б.Н. Квазигидродинамическая модель и мелкомасштабная турбулентность // Матем. моделирование. 2008. Т. 20. № 2. С. 13–20.

  6. Allmaras S.R., Johnson F.T., Spalart P.R. Modifications and Clarifications for the Implementation of the Spalart-Allmaras Turbulence Model. Seventh International Conference on CFD (ICCFD7), Big Island, Hawaii, 9–13 July 2012.

  7. Петров К.П. Аэродинамика транспортных космических систем. М.: Эдиториал УРСС, 2000. 368 с.

  8. Azarova O.A. Supersonic Flow Control Using Combined Energy Deposition // Aerospace. 2015. V. 2. P. 118–134. https://doi.org/10.3390/aerospace2010118

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал