1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 493, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 493, № 1, стр. 62-67

НОВАЯ ЯДЕРНО-ПРОЕКЦИОННАЯ СТАТИСТИЧЕСКАЯ ОЦЕНКА В МЕТОДЕ МОНТЕ-КАРЛО

Член-корреспондент РАН Г. А. Михайлов 1, 2, *, Н. В. Трачева 1, 2, **, С. А. Ухинов 1, 2

1 Институт вычислительной математики и математической геофизики Сибирского отделения Российской академии наук
Новосибирск, Россия

2 Новосибирский государственный университет
Новосибирск, Россия

* E-mail: gam@sscc.ru
** E-mail: tnv@osmf.sscc.ru

Поступила в редакцию 12.03.2020
После доработки 23.05.2020
Принята к публикации 23.05.2020

Полный текст (PDF)

Аннотация

Ядерная статистическая оценка в методе Монте-Карло обычно оптимизируется на основе предварительного построения “микровыборки” значений исследуемой переменной. Уже для двумерного случая такая оптимизация весьма затруднительна. Предлагается комбинированная (ядерно-проекционная) статистическая оценка двумерной плотности распределения: по первой (основной) переменной – ядерная, по второй – проекционная. При этом для каждого определенного по микровыборке “ядерного” интервала используются статистически оцененные коэффициенты некоторого ортогонального разложения условной плотности на основе предварительных соответствующих результатов для “микроинтервалов”. Важным результатом работы является среднеквадратическая оптимизация такой оценки при сделанных предположениях о скорости сходимости используемого ортогонального разложения. Верификация оценки реализована для двунаправленного распределения потока излучения, прошедшего через слой вещества.

Ключевые слова: ядерная статистическая оценка, проекционная оценка, ядерно-проекционная оценка, метод Монте-Карло

Пусть для начала необходимо оценить плотность f(x) распределения частиц (квантов излучения) по параметру x в конечном интервале ${{x}_{1}},~{{x}_{2}}$. Практически эффективной для этой цели может быть универсальная статистическая ядерная оценка Парзена–Розенблатта [1] с прямоугольным (“равномерным”) ядром (см. также [2]). Она строится на основе статистической оценки функционалов вида

${{J}_{\Delta }} = \int {f\left( {x{\kern 1pt} '} \right){{I}_{\Delta }}\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} ,$
где ${{I}_{\Delta }}\left( {x{\kern 1pt} '} \right)$ – индикатор интервала Δ = Δ(x) = = $\left( {x - \frac{{\delta }}{2}} \right.$, $\left. {x + \frac{{\delta }}{2}} \right)$. Предполагается, что постановка задачи допускает построение бернуллиевской оценки такого функционала путем подсчета числа ${{n}_{{\Delta }}}$ траекторий ${\Omega }$ частиц, невозвратно “посетивших” интервал ${\Delta }$. В задачах теории переноса частиц f(x) – это, в частности, стохастическая плотность распределения числа частиц в точках их “гибели”, например, вследствие невозвратного вылета из среды. Имеет место статистическая оценка ${{J}_{{\Delta }}} \approx \frac{{{{n}_{{\Delta }}}}}{N}$, где N – объем выборки {Ωk} (k = = $1,...,N)$.

Средний квадрат погрешности оценки f(x) ≈ ≈ $\frac{{{{n}_{{\Delta }}}}}{{N \cdot \delta }}$ равен (см., например, [2])

(1)
$\begin{gathered} {{\varepsilon }^{2}}\left( {x;N,\delta } \right) = {\text{E}}{{\left[ {f\left( x \right) - \frac{{{{n}_{{{\Delta (}x{\text{)}}}}}}}{{N\delta }}} \right]}^{2}} = {\text{D}}\left( {\frac{{{{n}_{{\Delta }}}}}{{N\delta }}} \right) + \\ \, + {{\left( {f\left( x \right) - \frac{{{{J}_{{\Delta }}}}}{\delta }} \right)}^{2}} \approx \frac{{f\left( x \right)}}{{N\delta }} + {{\left( {f{\kern 1pt} '{\kern 1pt} '\left( x \right)} \right)}^{2}}\frac{{{{\delta }^{4}}}}{{576}} \\ \end{gathered} $
с относительной погрешностью, убывающей до нуля при $\delta \to 0~$ и $N\delta \to \infty ~$. Минимизируя (1) соответственно [3], получаем

$\begin{gathered} \delta _{0}^{5}\left( x \right) = \frac{{144f\left( x \right)}}{{N{{{\left( {f{\kern 1pt} '{\kern 1pt} '\left( x \right)} \right)}}^{2}}}}, \\ {{\varepsilon }^{2}}\left( {x;N,~{{\delta }_{0}}} \right) \approx \frac{5}{4}\frac{{f\left( x \right)}}{{{{\delta }_{0}}\left( x \right)N}} \asymp {{N}^{{ - \frac{4}{5}}}}. \\ \end{gathered} $

Если реализуется весовое моделирование, то здесь f(x) – плотность распределения квадрата “веса” частиц, посетивших интервал Δ [3]. Отметим, что в [3] для оценки f(x) и $f{\kern 1pt} '{\kern 1pt} '\left( x \right)$ была использована наилучшая среднеквадратическая аппроксимация функции f(x) в интервале ${{{\Delta }}_{0}} \supset {\Delta }$ с помощью полиномов Лежандра порядков 0, 1, 2. Как и в [4], в работе [3] для оптимизации ядерной оценки была использована “микрогруппированная” выборка с шагом $h \ll \frac{\varepsilon }{{\mathop {\max }\limits_x \left| {f{\kern 1pt} '\left( x \right)} \right|}}$, где ε – требуемая погрешность оценки. При этом среднее число операций в алгоритме практически не зависит от δ.

1. Распространение этой методики на многомерный случай затруднительно из-за существенного увеличения объема микрогруппирования [4] и усложнения оптимизации оценки [1]. Поэтому здесь строится комбинированная статистическая оценка аналогичной двумерной плотности f(x, y), $x \in ({{x}_{1}},{{x}_{2}})$, $y \in ({{y}_{1}},{{y}_{2}})$ случайного вектора (ξ, η) при ${{x}_{2}} - {{x}_{1}},~{{y}_{2}} - {{y}_{1}} < + \infty $ в предположении, что справедливо “ортопроекционное” разложение

$f\left( {x,y} \right) = \mathop \sum \limits_{i = 0}^\infty {{a}_{i}}\left( x \right){{\psi }_{i}}\left( y \right),$
где $({{\psi }_{i}},{{\psi }_{j}}) = \int\limits_{{{y}_{1}}}^{{{y}_{2}}} {{{\psi }_{i}}\left( y \right){{\psi }_{j}}\left( y \right)dy} = {{J}_{{i,j}}}$ (${{J}_{{i,j}}}$ – символ Кронекера). При этом ${{\psi }_{0}}\left( y \right) \equiv \frac{1}{{\sqrt {{{y}_{2}} - {{y}_{1}}} }}$,

f1(x) = $\int\limits_{{{y}_{1}}}^{{{y}_{2}}} {f(x,y)dy} $ = ${{a}_{0}}(x)\sqrt {{{y}_{2}} - {{y}_{1}}} $.

Соответствующая статистическая оценка функции f(x, y) с учетом предложенной в [5] численно-статистической реализации проекционного разложения имеет вид

(2)
${{\tilde {f}}^{{\left( m \right)}}}\left( {x,y} \right) = \mathop \sum \limits_{i = 0}^m \frac{{\sum\limits_{k = 1}^N {{{I}_{{\Delta (x)}}}\left( {{{\xi }_{k}}} \right){{\psi }_{i}}\left( {{{\eta }_{k}}} \right)} }}{{N\delta }}{{\psi }_{i}}\left( y \right),$
где $\left\{ {{{\xi }_{k}},{{\eta }_{k}}} \right\}$ (k = 1, 2, …, N) – выборка случайных значений параметра (x, y), например значений “широтного” и “азимутального” углов направления частицы, вылетающей из среды. В случае весового моделирования значения ${{\psi }_{i}}\left( {{{\eta }_{k}}} \right)~$ умножаются на вес Qk.

Оценку (2) естественно назвать ядерно-проекционной. Нетрудно видеть, что

${\text{E}}{{\tilde {f}}^{{\left( m \right)}}}\left( {x,y} \right) \approx \mathop \sum \limits_{i = 0}^m {{a}_{i}}\left( x \right){{\psi }_{i}}\left( y \right).$

2. Среднеквадратическая погрешность оценки ${{\tilde {f}}^{{(m)}}}(x,y)$ определяется следующим образом:

$\begin{gathered} L\left( {N,\delta ,m} \right) = \mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} \mathop \smallint \limits_{{{y}_{1}}}^{{{y}_{2}}} {\text{E}}{{({{{\tilde {f}}}^{{\left( m \right)}}}\left( {x,y} \right) - f\left( {x,y} \right))}^{2}}dxdy = \\ \, = \mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} \mathop \smallint \limits_{{{y}_{1}}}^{{{y}_{2}}} \text{[}{{({\text{E }}{{{\tilde {f}}}^{{\left( m \right)}}} - f)}^{2}} + {\text{D }}{{{\tilde {f}}}^{{\left( m \right)}}}]dxdy, \\ \end{gathered} $
$\begin{gathered} {\text{E}}{{{\tilde {f}}}^{{\left( m \right)}}}\left( {x,y} \right) - f\left( {x,y} \right) = \frac{1}{\delta }\mathop \smallint \limits_{x - \frac{\delta }{2}}^{x + \frac{\delta }{2}} \left( {\mathop \sum \limits_{i = 0}^m {{a}_{i}}\left( {x{\kern 1pt} '} \right){{\psi }_{i}}\left( {y'} \right)} \right)dx{\kern 1pt} '\; - \\ \, - \mathop \sum \limits_{i = 0}^m {{a}_{i}}\left( x \right){{\psi }_{i}}\left( y \right) - \mathop \sum \limits_{i = m + 1}^\infty {{a}_{i}}\left( x \right){{\psi }_{i}}\left( y \right). \\ \end{gathered} $

Предположим, что $\left| {\mathop \sum \limits_{i = m + 1}^\infty {{a}_{i}}(x){{\psi }_{i}}(y)} \right| \lesssim $ F(x) · Sm, причем

(3)
${{S}_{m}}\xrightarrow[{m \to \infty }]{}0,\quad \mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} {{F}^{2}}\left( x \right)dx = \frac{{{{F}_{2}}}}{{{{y}_{2}} - {{y}_{1}}}} < + \infty .$

Тогда асимптотически при ${\delta } \to 0$, $N{\delta } \to \infty $, m $ \to \infty $ имеем

(4)
$\begin{gathered} \mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} \mathop \smallint \limits_{{{y}_{1}}}^{{{y}_{2}}} {\text{E}}{{({{{\tilde {f}}}^{{\left( m \right)}}} - f)}^{2}}dxdy \lesssim \\ \lesssim \mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} \mathop \sum \limits_{i = 0}^m {{(a_{i}^{{''}}\left( x \right))}^{2}}\frac{{{{\delta }^{4}}}}{{576}}dx + {{F}_{2}}S_{m}^{2}. \\ \end{gathered} $

Символ “$ \lesssim $” здесь и далее обозначает асимптотически приближенное неравенство, замена которого на равенство сохраняет порядок результативной погрешности относительно N. Оценка параметра F2 является сложной, однако далее показано, что соответствующая ошибка может слабо влиять на асимптотическую оптимизацию алгоритма. Соотношение (4) показывает, что здесь необходимо дополнительное ограничение:

$\mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} \mathop \sum \limits_{i = 0}^\infty {{(a_{i}^{{''}}(x))}^{2}}dx = \mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} {\text{||}}\,f_{{xx}}^{{''}}(x,y)\,{\text{||}}_{{L_{{2,y}}^{{}}}}^{2}dx < + \infty .$

Предполагается также, что коэффициенты $a_{i}^{{''}}\left( x \right)$, как и ${{a}_{i}}\left( x \right)$, убывают при i $ \to \infty $ достаточно быстро и приближенно равномерно в интервале $({{x}_{1}},{{x}_{2}})$; тем самым можно использовать оценку

${\text{||}}f_{{xx}}^{{''}}{\text{||}}_{{_{{{{L}_{{2,y}}}}}}}^{2} \lesssim C{\text{|}}a_{0}^{{''}}{{{\text{|}}}^{2}} = \frac{{C{\text{|}}f_{1}^{{''}}{{{\text{|}}}^{{{\text{ }}2}}}}}{{{{y}_{2}} - {{y}_{1}}}}.$

На этой основе получаем соотношение

$\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\int\limits_{{{y}_{1}}}^{{{y}_{2}}} {{\text{E}}{{{({{{\tilde {f}}}^{{\left( m \right)}}} - f)}}^{2}}dxdy} } \lesssim {{F}_{1}}{{\delta }^{4}} + {{F}_{2}}S_{m}^{2},$
где

(5)
${{F}_{1}} = \frac{{{{C}_{1}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {{{{(f_{1}^{{''}}{\text{(}}x{\text{)}})}}^{2}}} dx}}{{576}},\quad {{C}_{1}} = \frac{C}{{{{y}_{2}} - {{y}_{1}}}}.$

Отметим, что в первом приближении можно использовать ${{C}_{1}} = {{\left( {{{y}_{2}} - {{y}_{1}}} \right)}^{{ - 1}}}.$

3. Рассмотрим теперь второе слагаемое погрешности:

$\begin{gathered} {\text{D}}{{{\tilde {f}}}^{{\left( m \right)}}}\left( {x,y} \right) = \frac{1}{{N{{\delta }^{2}}}}\left[ {\mathop \sum \limits_{i = 0}^m {\text{D}}\left[ {{{I}_{{\Delta }}}\left( \xi \right){{\psi }_{i}}\left( \eta \right)} \right]\psi _{i}^{2}\left( y \right) + } \right. \\ \, + \left. {\mathop \sum \limits_{i \ne j} {\text{E}}\left[ {{{I}_{{\Delta }}}\left( \xi \right){{\psi }_{i}}\left( \eta \right){{\psi }_{j}}\left( \eta \right)} \right]{{\psi }_{i}}\left( y \right){{\psi }_{j}}\left( y \right)} \right], \\ \end{gathered} $
$\begin{gathered} \int\limits_{{{y}_{1}}}^{{{y}_{2}}} {{\text{D }}{{{\tilde {f}}}^{{\left( m \right)}}}dy} = \frac{1}{{N{{\delta }^{2}}}}\mathop \sum \limits_{i = 0}^m {\text{ D}}\left[ {{{I}_{{\Delta }}}\left( \xi \right){{\psi }_{i}}\left( \eta \right)} \right] \approx \\ \, \approx \frac{1}{{N{{\delta }^{2}}}}\mathop \sum \limits_{i = 0}^m {\text{E}}({{I}_{{\Delta }}}\left( \xi \right)\psi _{i}^{2}\left( \eta \right)), \\ \end{gathered} $
так как $\delta \ll 1$. Далее,

$\begin{gathered} {\text{E}}({{I}_{{\Delta }}}\left( \xi \right)\psi _{i}^{2}\left( \eta \right)) \approx \delta {{f}_{1}}\left( x \right){\text{E}}(\psi _{i}^{2}\left( \eta \right){{{\text{|}}}_{{\xi \in {\Delta }}}}) \approx \\ \, \approx \delta {{f}_{1}}\left( x \right)\mathop \smallint \limits_{{{y}_{1}}}^{{{y}_{2}}} \frac{{f\left( {x,y} \right)}}{{{{f}_{1}}(x)}}\psi _{i}^{2}\left( y \right)dy. \\ \end{gathered} $

Предполагая, что $0 < {{C}^{{\left( 1 \right)}}} < \frac{{f\left( {x,y} \right)}}{{{{f}_{1}}(x)}} < {{C}^{{\left( 2 \right)}}} < + \infty $, получаем соотношение

(6)
$\int {{\text{D }}{{{\tilde {f}}}^{{\left( m \right)}}}} dy \lesssim \frac{{{{F}^{{\left( 0 \right)}}}m{{f}_{1}}\left( x \right)}}{{N\delta }},\quad {{C}^{{\left( 1 \right)}}} < {{F}^{{\left( 0 \right)}}} < {{C}^{{\left( 2 \right)}}}.$

С сохранением порядка погрешности можно полагать ${{F}^{{\left( 0 \right)}}} = 0.5({{C}^{{\left( 1 \right)}}} + {{C}^{{\left( 2 \right)}}})$; в первом приближении можно использовать ${{F}^{{\left( 0 \right)}}} = {{\left( {{{y}_{2}} - {{y}_{1}}} \right)}^{{ - 1}}}$. Из сказанного выше следует, что для оптимизации алгоритма необходимо минимизировать величину среднего числа вычислительных операций вида $T = a \cdot m + b$ при условии, что

$L\left( {N,\delta ,m} \right) = {{F}_{0}}\frac{m}{{N\delta }} + {{F}_{1}}{{\delta }^{4}} + {{F}_{2}}S_{m}^{2} = {{\varepsilon }^{2}},$
где ${{F}_{0}} = {{F}^{{\left( 0 \right)}}}\mathop \smallint \limits_{{{x}_{1}}}^{{{x}_{2}}} {{f}_{1}}\left( x \right)dx,~$ величина ${{F}^{{\left( 0 \right)}}}$ определяется соотношением (6), F1 – соотношением (5), а F2 – соотношением (3).

Поскольку оптимизация по δ осуществляется на основе микрогруппированной выборки, то при надлежащей организации вычислений (см., например, [3]) значение T практически не зависит от δ. Оптимизация трудоемкости по δ таким образом сводится к минимизации величины $L(N,\delta ,m)$ по δ, которая, соответственно теории ядерных оценок, дает величину

(7)
$\begin{gathered} {{L}_{0}}\left( {N,m} \right) = \frac{5}{4}{{\left( {{{F}_{0}}\frac{m}{{4N{{F}_{1}}}}} \right)}^{{ - \frac{1}{5}}}}\frac{{m{{F}_{0}}}}{N} + {{F}_{2}}S_{m}^{2} = \\ \, = F \cdot {{\left( {\frac{m}{N}} \right)}^{{\frac{4}{5}}}} + {{F}_{2}}S_{m}^{2},\quad F = 5 \cdot {{4}^{{ - \frac{4}{5}}}}{{F}_{0}}^{{\frac{4}{5}}}{{F}_{1}}^{{\frac{1}{5}}}, \\ \end{gathered} $
причем

(8)
${{\delta }_{{opt}}} = {{\left( {{{F}_{0}}\frac{m}{{4N{{F}_{1}}}}} \right)}^{{\frac{1}{5}}}}$.

Проведенные исследования показали, что условная минимизация по m величины am + b при условии ${{L}_{0}}\left( {N,m} \right) = {{\varepsilon }^{2}}$ для реальных сложных задач весьма затруднительна. Поэтому далее осуществляется оптимизация в предположении, что свойства задачи и организация вычислений позволяют предположить, что среднее число операций практически не зависит от m, т.е. $\frac{{am}}{b} \ll 1$. Ясно, что такая оптимизация сводится к минимизации величины ${{L}_{0}}\left( {N,m} \right)$ по m.

4. Пусть ${{S}_{m}} \approx O({{m}^{{ - \left( {r - 1} \right)}}}).~$Такой вариант задачи рассмотрен в работе [5]. В [6] показано, что он реализуется для разложения r-кратно непрерывно дифференцируемой функции по тригонометрическим полиномам вследствие того, что при этом ai = O(i-r). Полагая $S_{m}^{2} = {{m}^{{ - 2\left( {r - 1} \right)}}}$, в результате минимизации ${{L}_{0}}\left( {N,m} \right)$ получаем

$m_{{opt}}^{{\left( 1 \right)}} = {{\left[ {\frac{5}{2}\frac{{{{F}_{2}}}}{F}\left( {r - 1} \right)} \right]}^{{\frac{1}{{2r - 1,2}}}}} \cdot {{N}^{{\frac{4}{{10r - 6}}}}}.$

Практически более реализуемой является оптимизация в предположении, что ${{S}_{m}} = O({{{\text{e}}}^{ - }}^{{\lambda m}})$, которое соответствует соотношению $\frac{{{{a}_{{i + 1}}}}}{{{{a}_{i}}}} \approx q,$ причем $\lambda = - \ln q,~$ ${{S}_{m}} \lesssim {{\tilde {F}}_{2}}{{{\text{e}}}^{ - }}^{{\lambda m}}$, ${{\tilde {F}}_{2}} = \frac{{{{a}_{0}}}}{{1 - {{{\text{e}}}^{ - }}^{\lambda }}}$. Такое предположение можно считать естественным для задачи оценки углового распределения частиц, испытавших многократное рассеяние в среде, которое оказывает “сглаживающее влияние”. Это подтверждает анализ результатов, полученных в [7]. Здесь оптимальное значение m = m0 определяется из уравнения

$ - \frac{4}{5}\ln N + \ln \left( {\frac{4}{5}F} \right) - \frac{1}{5}\ln m = \ln (2{{F}_{2}}\tilde {F}_{2}^{2}) - 2\lambda m.$

Асимптотически (при $N \to \infty $, ${{m}_{0}} \to \infty $) имеем

${{m}_{0}} \approx \frac{2}{5}\frac{{\ln N}}{\lambda } = \frac{2}{5}\frac{{\ln N}}{{\left| {\ln q} \right|}}.$

При этом, согласно (7), (8),

$\begin{gathered} {{\delta }_{{opt}}} = {{\left( {\frac{{{{F}_{0}}}}{{10{{F}_{1}}\left| {\ln q} \right|}}\frac{{\ln N}}{N}} \right)}^{{\frac{1}{5}}}}, \\ {{L}_{0}}(N,{{m}_{0}}) \approx F \cdot {{\left( {\frac{2}{{5\left| {\ln q} \right|}}\frac{{\ln N}}{N}} \right)}^{{\frac{4}{5}}}}, \\ \end{gathered} $
в то время как порядок оптимальной двумерной ядерной оценки с равномерным ядром определяется [2] величиной $\frac{1}{{{{N}^{{2/3}}}}}$.

5. Описанный выше подход был апробирован при решении задачи оценки углового распределения излучения, прошедшего через плоский слой $0 < z < H$ рассеивающего и поглощающего вещества от расположенного на границе z = 0 источника излучающего в заданном направлении ω0 = = $(0,\sin {{\theta }_{0}}$, cosθ0), где ${{\theta }_{0}} \in \left( {0,\frac{\pi }{2}} \right)$ – зенитный угол [8].

В качестве математической модели процесса переноса излучения рассматривается цепь Маркова столкновений фотонов с частицами вещества [9].

Для построения оценки типа (2) для плотности распределения потока излучения, выходящего из слоя через поверхность z = H, рассматривается разложение по ортонормированному тригонометрическому базису:

$\begin{gathered} {{\Phi }_{m}}\left( {\mu ,\varphi } \right) = ~\frac{{{{a}_{0}}\left( \mu \right)}}{{\sqrt {2\pi } }} + \mathop \sum \limits_{i = 1}^m {{a}_{{i~}}}\left( \mu \right) \cdot \frac{{\cos \left( {i~\varphi } \right)}}{{\sqrt \pi }} + \\ \, + \mathop \sum \limits_{i = 1}^m {{b}_{{i~}}}\left( \mu \right) \cdot \frac{{\sin \left( {i~\varphi } \right)}}{{\sqrt \pi }}. \\ \end{gathered} $

Здесь $\mu = \cos \theta $, $\theta $– зенитный угол, $\varphi $ – азимутальный угол, причем $\mu \in \left( {0,1} \right),$

$\begin{gathered} {{a}_{0}}\left( \mu \right) = ~\frac{1}{{\sqrt {2\pi } }}\int\limits_0^{2\pi } {{{\Phi }_{m}}\left( {\mu ,\varphi } \right)d\varphi } , \\ {{a}_{{i~}}}\left( \mu \right) = ~\frac{1}{{\sqrt \pi }}\int\limits_0^{2\pi } {{{\Phi }_{m}}\left( {\mu ,\varphi } \right)} \cdot \cos \left( {i~\varphi } \right)d\varphi , \\ {{b}_{{i~}}}\left( \mu \right) = ~\frac{1}{{\sqrt \pi }}\int\limits_0^{2\pi } {{{\Phi }_{m}}\left( {\mu ,\varphi } \right)} \cdot \sin \left( {i~\varphi } \right)d\varphi . \\ \end{gathered} $

В силу свойства симметрии искомой плотности относительно плоскости падения начального излучения φ = 0, коэффициенты ${{b}_{i}}$ здесь равны нулю. Для произвольной точки ${{\mu }_{k}} \in (0,1)$, коэффициенты разложения оцениваются с помощью ядерного осреднения по интервалу ${{\delta }_{{opt}}}$, полученному на основе предварительных оценок значений ${{F}_{0}}~$ и ${{F}_{1}}$ (см. пункты 2, 3).

В конкретном примере были реализованы следующие параметры: оптическая толщина слоя H = 4, ${{\theta }_{0}} = \frac{\pi }{4}$ и молекулярное рассеяние в среде [9]. По вычисленной микрогистограмме коэффициентов разложения по описанным выше формулам были получены оценки ${{F}_{0}}$ ≈ 0.00014 и ${{F}_{1}}$≈ 0.04. Быстрое убывание коэффициентов разложения ${{a}_{i}},$ i = 0, ..., m, позволило оценить оптимальное количество членов разложения: $m \approx 2,$ а также оптимальный шаг ядерного осреднения: ${{\delta }_{{opt}}} \approx 0,044$ для $N = {{10}^{9}}$ траекторий.

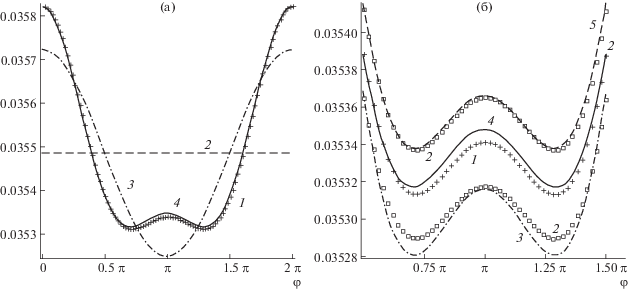
Для верификации построенной комбинированной оценки были проведены дополнительные расчеты значений функции интенсивности излучения с помощью локальной оценки метода Монте-Карло [9]. Численные результаты показали, что m = 2 действительно является оптимальным, поскольку добавление третьей гармоники не изменяет результат моделирования в пределах статистической погрешности, но увеличивает эту погрешность за счет большой погрешности оценки третьего коэффициента разложения. Данное свойство проиллюстрировано на рис. 1a. Проведенные расчеты с различными шагами ядерного осреднения δ подтвердили, что ${{\delta }_{{opt}}}$ ≈ 0.044 позволяет фактически получить наименее отклоняющуюся в пределах статистической погрешности оценку угловой плотности распределения. Данное утверждение проиллюстрировано на рис. 1б. Результаты расчетов предложенной в работе оценки хорошо согласуются с результатами локальной оценки, погрешность которой не превышает 0.03%.

Рис. 1.

Угловое распределение прошедшего через слой излучения для углов падения ${{\omega }_{0}} = \left( {0,\frac{1}{{\sqrt 2 }},\frac{1}{{\sqrt 2 }}} \right)$ и вылета $\omega {\kern 1pt} * = \left( {\frac{{\sqrt 3 }}{2}\sin \left( \varphi \right),\frac{{\sqrt 3 }}{2}\cos \left( \varphi \right),\frac{1}{2}} \right)$. (a) Линия 1 – локальная оценка, 2 – ${{\Phi }_{0}}\left( {\mu ,\varphi } \right),$ 3 – Φ1(μ, φ), 4 – Φ2(μ, φ). (б) 1 – локальная оценка, 2 – доверительный интервал $3\sigma $ для локальной оценки, 3 – Φ2(μ, φ) для δ ≈ 0.0841, 4 – Φ2(μ, φ) для ${{\delta }_{{opt}}}$≈ 0.044, 5 – Φ2(μ, φ) для δ ≈ 0.0396.

Список литературы

  1. Епанечников В.А. Непараметрическая оценка многомерной плотности вероятности // Теория вероятностей и ее применения. 1969. Т. 14. № 1. С. 156–161.

  2. Боровков А.А. Математическая статистика. Новосибирск: Наука, 1997. 771 с.

  3. Михайлов Г.А., Пригарин М., Роженко С.А. Модификации стандартной векторной оценки метода Монте-Карло для исследования характеристик рассеянного поляризованного излучения // ДАН. 2017. Т. 476. № 3. С. 264–286.

  4. Lotova G.Z. Monte Carlo Algorithms for Calculation of Diffusive Characteristics of an Electron Avalanche in Gases // Russian J. Mathematical and Mathematical Modelling. 2016. V. 31. № 6. P. 369–377.

  5. Ченцов Н.Н. Статистические решающие правила и оптимальные выводы. М.: Наука, 1972. 520 с.

  6. Смелов В.В. Задачи Штурма–Лиувилля и разложения функций в быстросходящиеся ряды. Новосибирск: Изд-во СО РАН; 2000. 144 с.

  7. Михайлов Г.А., Трачева Н.В., Ухинов С.А. Рандомизированный проекционный метод для оценки угловых распределений поляризованного излучения на основе численного статистического моделирования // ЖВМи МФ. 2016. Т. 56. № 9. С. 1560–1570.

  8. Tracheva N.V., Ukhinov S.A. On the evaluation of spatial–angular distributions of polarization characteristics of scattered radiation // Statistical Papers. 2018. V. 59. № 4. P. 1541–1557.

  9. Марчук Г.И., Михайлов Г.А., Назаралиев М.А., Дарбинян Р.А., Каргин Б.С. Метод Монте-Карло в атмосферной оптике. Новосибирск: Наука, 1976. 284 с.

  10. Сибирский суперкомпьютерный центр ИВМиМГ СО РАН. [Электронный ресурс]. URL. http://www.sscc.icmmg.nsc.ru/ (дата обращения 03.03.2020).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал