Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 493, № 1, стр. 26-31

О ДВИЖЕНИИ, УСИЛЕНИИ И РАЗРУШЕНИИ ФРОНТОВ В УРАВНЕНИЯХ ТИПА БЮРГЕРСА С КВАДРАТИЧНОЙ И МОДУЛЬНОЙ НЕЛИНЕЙНОСТЬЮ

Н. Н. Нефедов^1, *, академик РАН О. В. Руденко^{1, 2, 3, **}

¹ Московский государственный университет имени М.В. Ломоносова
Москва, Россия

² Институт общей физики им. А.М. Прохорова Российской академии наук
Москва, Россия

³ Институт физики Земли им. О.Ю. Шмидта Российской академии наук
Москва, Россия

^* E-mail: nefedov@phys.msu.ru
^** E-mail: rudenko@acs366.phys.msu.ru

Поступила в редакцию 26.05.2020
После доработки 08.06.2020
Принята к публикации 09.06.2020

DOI: 10.31857/S2686954320040141

Полный текст (PDF)

Аннотация

Рассмотрена сингулярно возмущенная начально-краевая задача для параболического уравнения, называемого в приложениях уравнением типа Бюргерса. Получены условия существования и построено асимптотическое приближение нового класса решений с движущимся фронтом. Результаты применены для задач с квадратичной и модульной нелинейностью при нелинейном усилении. Выявлено влияние нелинейного усиления на процессы распространения и разрушения фронтов. Получены оценки локализации и времени разрушения.

Ключевые слова: сингулярно возмущенные параболические задачи, уравнения типа Бюргерса, уравнения реакция–диффузия–адвекция, внутренние слои, фронты, асимптотические методы, разрушение решений

1. ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ

Уравнение Бюргерса (см. [1]) и уравнения типа уравнения Бюргерса давно и широко используются в моделировании таких физических систем, как газовая динамика, нелинейная акустика, турбулентность, волны на мелкой воде и в других прикладных задачах. Оно также используются в нелинейных уравнениях с частными производными при описании бегущих волн, слабых ударных волн и при разработке численных методов для параболических и гиперболических уравнений (см. [2–5]). Вопросы устойчивости решений типа бегущих волн исследовались в [6]), пионерские результаты по теории обострения и разрушения решений изложены в [7] (см. также ссылки в этой работе).

Предлагаемая работа посвящена исследованию решений с внутренним переходным слоем уравнения вида

(1)

$\begin{gathered} \varepsilon \frac{{{{\partial }^{2}}u}}{{\mathop {\partial x}\nolimits^2 }} - \frac{{\partial u}}{{\partial t}} = \frac{{\partial \left( {\tfrac{\beta }{2}{{u}^{2}} + \gamma \left| u \right|} \right)}}{{\partial x}} - \alpha f(u,x,t), \\ x \in (0,1),\quad t \in (0,T], \\ \end{gathered} $

где $\varepsilon $ – безразмерный малый параметр, $\alpha $, $\beta $ и $\gamma $ – некоторые постоянные. В случае α = 0, γ = 0 это уравнение Бюргерса, в случае α = 0, β = 0 – так называемое уравнение типа Бюргерса с модульной нелинейностью [8, 9], в случае $\alpha \ne 0$ – уравнение типа Бюргерса с усилением (случай кубического усиления $f(u,x,t) = {{u}^{3}}$ рассмотрен нами в [10]). Отметим, что случай модульной нелинейности представляет интерес как для ряда приложений в механике структурно-неоднородных, многофазных сред, композитов и метаматериалов [11], так и как более простая для аналитических рассмотрений модель в задачах с переходным слоем [12].

Рассматривается постановка, аналогичная постановке задачи для уравнения Бюргерса:

(2)

$\begin{gathered} u(0,t,\varepsilon ) = {{u}^{0}}(t),\quad u(1,t,\varepsilon ) = {{u}^{1}}(t),\quad t \in [0,T], \\ u(x,0,\varepsilon ) = {{u}_{{init}}}(x,\varepsilon ),\quad x \in [0,1]. \\ \end{gathered} $

Начальная функция ${{u}_{{init}}}(x,\varepsilon )$ представляет собой сформировавшийся фронт (резкий переходный слой) в окрестности некоторой заданной точки ${{x}_{{00}}}$ между заданными уровнями, и требуется описать движение фронта со временем. В теории нелинейных волн более естественной является постановка начально-краевой задачи, когда в (1), (2) время и координата меняются местами (“волновая постановка”). Тогда уравнение описывает квадратично нелинейные или модульные волны в среде без дисперсии с нелинейным усилением (см. [8, 9]). Особенностью нашей постановки является то, что начальное условие для задачи (1) задается в виде сформировавшегося фронта с внешними ветвями, приближаемыми решениями упрощенного уравнения (при ε = 0), зависящими не только от $x$ (от $t$ в “волновой постановке”), но и от $t$ (от $x$ в “волновой постановке”). Это главное отличие рассматриваемой задачи от задачи в [10]. Такие фронты имеют более сложную структуру.

2. РЕЗУЛЬТАТЫ АСИМПТОТИЧЕСКОГО АНАЛИЗА УРАВНЕНИЙ ТИПА БЮРГЕРСА

В этом разделе приведены результаты, которые развивают исследования работ [13] по существованию и описанию фронтов в более общих, чем (1), (2), задачах вида

(3)

$\begin{gathered} \varepsilon \frac{{{{\partial }^{2}}u}}{{\mathop {\partial x}\nolimits^2 }} - \frac{{\partial u}}{{\partial t}} = A(u,x,t)\frac{{\partial u}}{{\partial x}} + B(u,x,t), \\ x \in (0,1),\quad t \in (0,T], \\ u(0,t,\varepsilon ) = {{u}^{0}}(t),\quad u(1,t,\varepsilon ) = {{u}^{1}}(t),\quad t \in [0,T], \\ u(x,0,\varepsilon ) = {{u}_{{init}}}(x,\varepsilon ),\quad x \in [0,1]. \\ \end{gathered} $

Отметим, что вопросы существования периодических решений с внутренним переходным слоем и их устойчивости по Ляпунову в задаче типа (3) в случае медленно меняющихся коэффициентов исследовались в [14]. Исследования основывались на результатах общей схемы асимптотического принципа сравнения (см., например, [15]).

2.1. Условия существования фронта

Сформулируем условия, при которых задача (3) имеет решение в виде движущегося фронта.

Предполагаем (как и в [10]), что в начальный момент времени уже существует сформированный фронт, т.е. функция ${{u}_{{init}}}(x,\varepsilon )$ имеет внутренний переходный слой в окрестности некоторой точки ${{x}_{{00}}}$ отрезка [0; 1]. Нас интересует существование решения в виде движущегося фронта, т.е. решения, имеющего внутренний переходный слой, который в каждый момент времени $t$ локализован в окрестности точки $\hat {x}(t,\varepsilon ) \in (0,1)$. Слева от указанной окрестности решение $u(x,t,\varepsilon )$ задачи (3) близко к решению дифференциального уравнения

(4)

$\frac{{\partial u}}{{\partial t}} + A(u,x,t)\frac{{\partial u}}{{\partial x}} + B(u,x,t) = 0$

с дополнительным условием $u(0,t) = {{u}^{0}}(t)$, а справа от указанной окрестности близко к решению уравнения (4) с дополнительным условием $u(1,t)$ = = u¹(t).

Существование этих решений обеспечивается следующим требованием.

(H₁). Уравнение (4) с дополнительным условием $u(0,t)$ = u⁰(t) имеет решение $u = {{\varphi }^{l}}(x,t)$, а с дополнительным условием $u(1,t) = {{u}^{1}}(t)$ – решение u = ${{\varphi }^{r}}(x,t)$, причем эти решения определены и удовлетворяют неравенствам

${{\varphi }^{l}}(x,t) < {{\varphi }^{r}}(x,t),\quad A({{\varphi }^{l}}(x,t),x,t) > 0,$

$A({{\varphi }^{r}}(x,t),x,t) < 0\quad при\quad x \in [0,1],\quad t \in [0,T].$

Точка $(\hat {x},t)$ описывает на плоскости (x, t) некоторую кривую $x = \hat {x}(t,\varepsilon )$, которая определяет положение внутреннего переходного слоя на отрезке $[0;\;1]$ в каждый фиксированный момент времени $t \in (0;T]$ как точку пересечения решения $u(x,t$, ε) с кривой $u = \varphi (x,t)$, ${{\varphi }^{l}}(x,t) < \varphi (x,t)$ < φ^r(x, t):

$u\left( {\hat {x}(t,\varepsilon ),\varepsilon } \right) = \varphi (\hat {x}(t,\varepsilon )),$

а $u = \varphi (x,t)$ определим стандартно как полусумму функций ${{\varphi }^{l}}(x,t)$ и ${{\varphi }^{r}}(x,t)$.

Потребуем также выполнения следующих условий.

(H₂). Пусть

$\begin{gathered} \int\limits_{{{\varphi }^{l}}(x)}^s {A(u,x,t)} du > 0\quad при\quad s \in ({{\varphi }^{l}}(x,t),{{\varphi }^{r}}(x,t)], \\ x \in [0,1]\quad t \in [0,T], \\ \end{gathered} $

и пусть задача

(5)

$\frac{{d{{x}_{0}}}}{{dt}} = \frac{{\int\limits_{{{\varphi }^{l}}({{x}_{0}},t)}^{{{\varphi }^{r}}({{x}_{0}},t)} A (u,{{x}_{0}},t)du}}{{{{\varphi }^{r}}\left( {{{x}_{0}},t} \right) - {{\varphi }^{l}}\left( {{{x}_{0}},t} \right)}} \equiv V({{x}_{0}},t),\quad {{x}_{0}}(0) = {{x}_{{00}}},$

где ${{x}_{{00}}} \in (0,1)$, имеет решение ${{x}_{0}}(t)$ такое, что

${{x}_{0}}(t) \in (0,1)\quad при\quad t \in [0;T].$

Основным результатом для задачи (3) при перечисленных выше условиях является теорема существования и асимптотическое приближение решения типа движущегося фронта с главным членом в описании положения фронта ${{x}_{0}}(t)$. Отметим, что в работе [10] рассматривался случай, когда ${{\varphi }^{l}}$ и ${{\varphi }^{r}}$ (и, следовательно, V) зависели только от $x$. Было установлено, что асимптотически устойчивые стационарные точки уравнения движения

$\frac{{d{{x}_{0}}}}{{dt}} = V({{x}_{0}})$

соответствуют асимптотически устойчивым стационарным решениям исходной параболической задачи с переходным слоем, локализованным в окрестности этих точек, и показано, что точки разрушения решения этого уравнения соответствуют точкам разрушения (обострения) решения исходной задачи в окрестности кривой переходного слоя. В рассматриваемом случае распространение фронта и его структура имеют более сложный характер (см. условие $({{H}_{1}})$ и уравнение (5)).

Главный член асимптотики решения задачи (3) ${{U}_{0}}(x,t,\varepsilon )$ имеет вид

(6)

$\begin{gathered} {{U}_{0}}(x,t,\varepsilon ) = \\ = \;\left\{ \begin{gathered} U_{0}^{l}(x,t,\varepsilon ) = {{\varphi }^{l}}(x,t) + Q_{0}^{l}(\xi ,t),\quad 0 \leqslant x \leqslant {{x}_{0}}(t), \hfill \\ U_{0}^{r}(x,t,\varepsilon ) = {{\varphi }^{r}}(x,t) + Q_{0}^{r}(\xi ,t),\quad {{x}_{0}}(t) \leqslant x \leqslant 1, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

где $\xi = \tfrac{{x - {{x}_{0}}(t)}}{\varepsilon }$, а $Q_{0}^{{l,r}}(\xi ,t)$ – функции переходного слоя в окрестности кривой ${{x}_{0}}(t)$ определяются из уравнений для функций $Q_{0}^{l}(\xi ,t)$ при $\xi \leqslant 0$ и $Q_{0}^{r}(\xi ,t)$ при $\xi \geqslant 0$:

(7)

$\begin{gathered} \frac{{{{\partial }^{2}}Q_{0}^{{l,r}}}}{{\mathop {\partial \xi }\nolimits^2 }} - (A({{\varphi }^{{l,r}}}({{x}_{0}}(t),t) + \\ + \;Q_{0}^{{l,r}},{{x}_{0}}(t),t) - V({{x}_{0}},t))\tfrac{{\partial Q_{0}^{{l,r}}}}{{\partial \xi }} = 0 \\ \end{gathered} $

с дополнительными условиями

(8)

$\begin{gathered} Q_{0}^{l}(0,t) + {{\varphi }^{l}}({{x}_{0}}(t),t) = Q_{0}^{r}(0,t) + \\ + \;{{\varphi }^{r}}({{x}_{0}}(t),t) = \varphi ({{x}_{0}}(t),t), \\ Q_{0}^{l}(\xi ,t) \to 0\quad {\text{при}}\quad \xi \to - \infty , \\ Q_{0}^{r}(\xi ,t) \to 0\quad {\text{при}}\quad \xi \to + \infty ,\quad t \in (0;T]. \\ \end{gathered} $

В силу условия (H₁) задачи для функций переходного слоя $Q_{0}^{{l,r}}$ разрешимы, и для них имеют место экспоненциальные оценки

(9)

$\begin{gathered} {\text{|}}Q_{0}^{l}(\xi ,t){\text{|}} \leqslant C{{e}^{{\kappa \xi }}},\quad \xi \leqslant 0, \\ {\text{|}}Q_{0}^{r}(\xi ,t){\text{|}} \leqslant C{{e}^{{ - \kappa \xi }}},\quad \xi \geqslant 0,\quad 0 \leqslant t \leqslant T, \\ \end{gathered} $

где С и $\kappa $ – некоторые положительные числа.

2.2. Условия разрушения фронта

Поведение решения в рассматриваемом случае (в том числе поведение решений вырожденных задач условия (H₁): ${{\varphi }^{l}}(x,t)$ и ${{\varphi }^{r}}(x,t)$) более сложное, чем рассмотренное в [10]. Ниже выделим случай, аналогичный рассмотренному в [10], когда разрушение фронта происходит через увеличение скачка решения в переходном слое. Представляется, что этот случай интересен как для приложений, так и для теории возмущений.

Пусть выполнено условия (H₁) при $0 \leqslant t < {{t}_{c}}$. Заменим условие H₂ на условие

$(H_{2}^{*})$. Пусть задача

(10)

$\begin{gathered} \frac{{dx}}{{dt}} = \frac{{\int\limits_{{{\varphi }^{l}}(x,t)}^{{{\varphi }^{r}}(x,t)} A (u,x,t)du}}{{{{\varphi }^{r}}\left( {x,t} \right) - {{\varphi }^{l}}\left( {x,t} \right)}} \equiv V(x,t), \\ x(0) = {{x}_{{00}}},\quad {{x}_{{00}}} \in (0,\;1) \\ \end{gathered} $

имеет решение $x = {{x}_{0}}(t)$ такое, что

${{x}_{0}}(t) \in (0,1)\quad при\quad t \in [0,{{t}_{c}}).$

Условие H₁ дополним условием

$(H_{1}^{*})$. Уравнение (4) с условием $u(0,t) = {{u}^{0}}(t)$ имеет решение $u = {{\varphi }^{l}}(x,t)$ такое, что ${{\varphi }^{l}}({{x}_{0}}(t),t) \to - \infty $ для $t \to {{t}_{c}}$, а с условием $u(1,t) = {{u}^{1}}(t)$ имеет решение $u = {{\varphi }^{r}}(x,t)$, $x \in [0,\;1]$, $t \in [0,{{t}_{c}})$, причем

${{\varphi }^{l}}(x,t) < {{\varphi }^{r}}(x,t),\quad x \in [0,1),\quad t \in [0,{{t}_{c}}),$

$A({{\varphi }^{l}}(x,t),x,t) > 0,\quad A({{\varphi }^{r}}(x,t),x,t) < 0.$

Следствие 1. Из результатов раздела 2.1 и условий $(H_{1}^{ * })$ и $(H_{2}^{ * })$ следует, что решение задачи (3) имеет обострение (разрушение) – стремящийся к бесконечности скачок амплитуды на фронте в окрестности точки ${{x}_{0}}({{t}_{c}})$ при времени $t \to {{t}_{c}}$.

Замечание 1. Аналогично рассматриваются случаи, когда разрушается ${{\varphi }^{r}}$ или ${{\varphi }^{l}}$ и ${{\varphi }^{r}}$. Второй случай типичен для волновой постановки (см. также [10]).

3. УРАВНЕНИЕ БЮРГЕРСА С КУБИЧЕСКИМ УСИЛЕНИЕМ

Здесь рассматривается конкретная задача вида (3):

(11)

$\begin{gathered} \varepsilon \frac{{{{\partial }^{2}}u}}{{\mathop {\partial x}\nolimits^2 }} - \frac{{\partial u}}{{\partial t}} = - u\frac{{\partial u}}{{\partial x}} - {{u}^{3}},\quad x \in (0,1),\quad t \in (0,T], \\ u(0,t,\varepsilon ) = {{u}^{0}}(t),\quad u(1,t,\varepsilon ) = {{u}^{1}}(t),\quad t \in [0,T], \\ u(x,0,\varepsilon ) = {{u}_{{init}}}(x,\varepsilon ),\quad x \in [0,1]. \\ \end{gathered} $

3.1. Условия существования фронта

При выполнении условий H₁ и H₂${{x}_{0}}(t)$ определяется из задачи (5), которая принимает вид

(12)

$\begin{gathered} \frac{{d{{x}_{0}}}}{{dt}} = - \frac{{{{\varphi }^{r}}({{x}_{0}},t) + {{\varphi }^{l}}({{x}_{0}},t)}}{2}, \\ {{x}_{0}}(0) = {{x}_{{00}}},\quad {{x}_{{00}}} \in (0,1). \\ \end{gathered} $

Очевидно, если ${{\varphi }^{r}}({{x}_{0}},t) + {{\varphi }^{l}}({{x}_{0}},t) = 0$, то ${{x}_{0}}(t)$ = x₀₀.

3.2. Условия разрушения фронта

Если условия $H_{1}^{ * }$ и $H_{2}^{ * }$ выполняются, то решение задачи (11) имеет обострение (разрушение) – стремящийся к бесконечности скачок амплитуды на фронте в окрестности точки ${{x}_{0}}({{t}_{c}})$ при времени $t \to {{t}_{c}}$.

4. ФРОНТЫ, ОПИСЫВАЕМЫЕ УРАВНЕНИЕМ БЮРГЕРСА С МОДУЛЬНОЙ НЕЛИНЕЙНОСТЬЮ

Предложенная схема асимптотического анализа применима и для уравнений Бюргерса с модульной нелинейностью (адвекцией модульного типа). Задачи такого типа для уравнения Бюргерса рассматривались в [6–8] и [12].

Здесь рассматривается задача

(13)

$\begin{gathered} \varepsilon \frac{{{{\partial }^{2}}u}}{{\mathop {\partial x}\nolimits^2 }} - \frac{{\partial u}}{{\partial t}} = - \frac{{\partial {\text{|}}u{\text{|}}}}{{\partial x}} + B(u,x,t), \\ x \in (0,1),\quad t \in (0,T], \\ u(0,t,\varepsilon ) = {{u}^{0}}(t) < 0, \\ u(1,t,\varepsilon ) = {{u}^{1}}(t) > 0,\quad t \in [0,T], \\ u(x,0,\varepsilon ) = {{u}_{{init}}}(x,\varepsilon ),\quad x \in [0,1]. \\ \end{gathered} $

В этом случае уравнение (4) имеет вид

(14)

$\frac{{\partial u}}{{\partial t}} - \frac{{\partial \left| u \right|}}{{\partial x}} + B(u,x,t) = 0.$

4.1. Условия существования фронта

Условия $({{H}_{1}})$ и $({{H}_{2}})$ существования фронтов в задаче (3) заменяются на условия:

$({{H}_{{1m}}})$. Уравнение (14) с дополнительным условием $u(0,t) = {{u}^{0}}(t)$ имеет решение $u = {{\varphi }^{l}}(x,t) < 0$, а с дополнительным условием $u(1,t) = {{u}^{1}}(t)$ – решение $u = {{\varphi }^{r}}(x,t) > 0$, определенные при $x \in [0,1]$, $t \in [0,T]$.

$({{H}_{{2m}}})$. Пусть задача

$\begin{gathered} \frac{{d{{x}_{0}}}}{{dt}} = \frac{{{{\varphi }^{r}}({{x}_{0}},t) + {{\varphi }^{l}}({{x}_{0}},t)}}{{{{\varphi }^{r}}\left( {{{x}_{0}},t} \right) - {{\varphi }^{l}}\left( {{{x}_{0}},t} \right)}} \equiv V({{x}_{0}},t), \\ {{x}_{0}}(0) = {{x}_{{00}}},\quad {{x}_{{00}}} \in (0,1) \\ \end{gathered} $

имеет решение ${{x}_{0}}(t)$ такое, что

${{x}_{0}}(t) \in (0,1)\quad при\quad t \in [0;T].$

Главный член асимптотики решения имеет вид (6), при этом $Q_{0}^{{l,r}}(\xi ,t)$ определяются из задач

(15)

$\frac{{{{\partial }^{2}}Q_{0}^{{l,r}}}}{{\mathop {\partial \xi }\nolimits^2 }} - \left( {\frac{{ - 2{{\varphi }^{{l,r}}}({{x}_{0}},t)}}{{{{\varphi }^{r}}\left( {{{x}_{0}},t} \right) - {{\varphi }^{l}}\left( {{{x}_{0}},t} \right)}}} \right)\frac{{\partial Q_{0}^{{l,r}}}}{{\partial \xi }} = 0$

с дополнительными условиями

$\begin{array}{*{20}{c}} {Q_{0}^{l}(0,t) + {{\varphi }^{l}}({{x}_{0}}(t),t) = Q_{0}^{r}(0,t) + {{\varphi }^{r}}({{x}_{0}}(t),t) = 0,} \\ \begin{gathered} Q_{0}^{l}(\xi ,t) \to 0\quad {\text{при}}\quad \xi \to - \infty , \\ Q_{0}^{r}(\xi ,t) \to 0\quad {\text{при}}\quad \xi \to + \infty ,\quad t \in (0;T]. \\ \end{gathered} \end{array}$

Условия разрушения фронта в задаче (13) $(H_{{1m}}^{ * })$ и $(H_{{2m}}^{ * })$ получаются из $({{H}_{{1m}}})$ и $({{H}_{{2m}}})$ так же, как получались аналогичные условия в задаче (3).

5. НЕЛИНЕЙНЫЕ ВОЛНЫ, ОПИСЫВАЕМЫЕ УРАВНЕНИЕМ БЮРГЕРСА С МОДУЛЬНОЙ НЕЛИНЕЙНОСТЬЮ И КУБИЧНО НЕЛИНЕЙНЫМ УСИЛЕНИЕМ

Рассмотрим задачу (13), когда $B(u,x,t)$ = –αu³. В этом случае уравнение (14) имеет вид

(16)

$\frac{{\partial u}}{{\partial t}} - \frac{{\partial \left| u \right|}}{{\partial x}} - \alpha {{u}^{3}} = 0.$

Рассмотрим ситуацию, когда при t = 0 решение соответствующих задач для ${{\varphi }^{l}}(x,0)$ и ${{\varphi }^{r}}(x,0)$ определяется начальным условием $u(x,0) = V(x)$ в некоторой области изменения x, которая будет уточнена ниже. Это решение уравнения (16) имеет вид

${{\varphi }^{{r,l}}}(x,t) = \pm \frac{{V(x \pm t)}}{{{{{(1 - \alpha t{{V}^{2}}(x \pm t))}}^{{\tfrac{1}{2}}}}}}$

и определяет движение фронта в некоторой области. Для конкретности проанализируем поведение гармонической волны $V(x) = sin(x)$ при $ - \tfrac{{7\pi }}{{12}} \leqslant x \leqslant \tfrac{{7\pi }}{{12}}$ и выберем $\alpha = \tfrac{2}{\pi }$. Следовательно,

(17)

$\begin{gathered} {{\varphi }^{r}}(x,t) = \frac{{sin(x + t)}}{{{{{(1 - \alpha tsi{{n}^{2}}(x + t))}}^{{\frac{1}{2}}}}}}, \\ {{\varphi }^{l}}(x,t) = \frac{{sin(x - t)}}{{{{{(1 - \alpha tsi{{n}^{2}}(x - t))}}^{{\frac{1}{2}}}}}}. \\ \end{gathered} $

Фронт с начальным положением ${{x}_{{00}}} = 0$ распространяется вдоль прямой x = 0. Несложно устанавливается, что ${{\varphi }^{{r,l}}}({{x}_{0}}(t),t)$ разрушаются при t = $\tfrac{\pi }{3}$.

Главный член асимптотики решения задачи (13) ${{U}_{0}}(x,t)$ имеет вид, аналогичный представлению (6):

$\begin{gathered} {{U}_{0}}(x,t) = \\ = \;\left\{ \begin{gathered} U_{0}^{l}(x,t) = {{\varphi }^{l}}(x,t) + Q_{0}^{l}(0,\xi ),\quad - \tfrac{{7\pi }}{{12}} \leqslant x \leqslant 0, \hfill \\ U_{0}^{r}(x,t) = {{\varphi }^{r}}(x,t) + Q_{0}^{r}(0,\xi ),\quad 0 \leqslant x \leqslant \tfrac{{7\pi }}{{12}}, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

где $\xi = \tfrac{x}{\varepsilon }$, ${{\varphi }^{{l,r}}}(x,t)$ определены выражениями (17), а $Q_{0}^{{l,r}}(x,\xi )$ – функции переходного слоя в окрестности прямой $x = 0$, определяются из задач, аналогичных задачам (7), (8). Уравнения для их определения имеет вид (см. (15))

$\frac{{{{\partial }^{2}}Q_{0}^{{l,r}}}}{{\mathop {\partial \xi }\nolimits^2 }} \mp \frac{{\partial Q_{0}^{{l,r}}}}{{\partial \xi }} = 0.$

Решение этих задач находится в явном виде:

$\begin{gathered} Q_{0}^{l}(0,t,\xi ) = - {{\varphi }^{l}}(0,t)exp\left( { - \left| \xi \right|} \right), \\ Q_{0}^{r}(0,t,\xi ) = - {{\varphi }^{r}}({{t}_{0}})exp(\xi ). \\ \end{gathered} $

Таким образом, разрушения фронтов при $t \to {{t}_{c}}$ = = $\tfrac{\pi }{3}$ происходит за счет роста амплитуды скачка в переходном слое. Очевидно, что в рассматриваемом случае при произвольных $\alpha $ величина “скачка” на ударном фронте определяется

${{\varphi }^{r}}(0,t) = - {{\varphi }^{l}}(0,t) \equiv \varphi (t) = \frac{{sin(t)}}{{{{{(1 - \alpha tsi{{n}^{2}}(t))}}^{{\tfrac{1}{2}}}}}}.$

Поведение “амплитуды” разрыва показано на рис. 1 для различных значений коэффициента усиления α.

Рис. 1.

Изменение со временем амплитуды скачка для различных значений коэффициента усиления α = 0; 0.2; 0.3; 0.5 (кривые 1–4 соответственно).

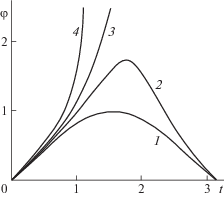
Видно, что при слабом усилении величина скачка конечна при любых значениях $t$. Для достаточно больших значений α, больших некоторого критического значения ${{\alpha }_{{cr}}}$, при которых уравнение

$tsi{{n}^{2}}(t) = \frac{1}{{2\alpha }}$

имеет решение, величина скачка стремится к бесконечности при значении $t \to {{t}_{{bl}}}$, где ${{t}_{{bl}}}$ – решение уравнения при фиксированном $\alpha > {{\alpha }_{{cr}}}$.

6. ЗАКЛЮЧЕНИЕ

Предлагаемый подход позволит получить важные для приложений результаты по движению и разрушению фронтов и в других задачах, в частности, интересном для приложений случае совместного вхождения различных нелинейностей (см. [8]), а также другие законы нелинейного усиления. Явные асимптотические приближения для решений позволяют, на наш взгляд, эффективно решать некоторые типы обратных задач по нахождению параметров моделей. Развитие этого подхода предполагается в направлении изучения других более сложных начально-краевых условий, характерных для многих приложений нелинейной теории волн.

Список литературы

Burgers J.M. A Mathematical Model Illustrating the Theory of Turbulence // Advances in Applied Mechanics. 1948. V. 1. P. 171–199.
Parker A. On the Periodic Solution of the Burgers Equation: A Unified Approach // Proc. R. Soc. Lond. A. 1992. V. 438. P. 113–132.
Cole J.D. On a Quasilinear Parabolic Equation Occurring in Aerodynamics // Quart. Appl. Math. 1951. V. 9. P. 225–236.
Fahmy E.S., Raslan K.R., Abdusalam H.A. On the Exact and Numerical Solution of the Time-Delayed Burgers Equation // Int. J. Comput. Math. 2008. V. 85. P. 1637–1648.
Rudenko O.V., Gurbatov S.N., Hedberg C.M. Nonlinear Acoustics Through Problems and Examples. Trafford, Victoria. 2011.
Volpert A.I., Volpert V.A., Volpert V.A. Traveling Wave Solutions of Parabolic Systems. Translatio edition. Providence, Rhode Island: American Mathematical Society, 1994. V. 140. P. 448.
Samarskii A.A., Galaktionov V.A., Kurdyumov S.P., Mikhailov A.P. Blow-up in Quasilinear Parabolic Equations. B.: Walter de Gruyter, 1995.
Руденко О.В. Линеаризуемое уравнение для волн в диссипативных средах с модульной, квадратичной и квадратично-кубичной нелинейностями // ДАН. 2016. Т. 471. № 1. С. 23–27.
Руденко О.В. Модульные солитоны // ДАН. 2016. Т. 471. № 6. С. 451–454.
Нефедов Н.Н., Руденко О.В. О движении фронта в уравнении типа Бюргерса с квадратичной и модульной нелинейностью при нелинейном усилении // ДАН. 2018. Т. 478. № 3. С. 274–279.
Амбарцумян С.А. Разномодульная теория упругости. М.: Наука, 1982. 318 с.
Hedberg C.M., Rudenko O.V. Collisions, Mutual Losses and Annihilation of Pulses in a Modular Nonlinear Medium // Nonlinear Dyn. 2017. V. 90. P. 2083–2091.
Антипов Е.А., Левашова Н.Т., Нефедов Н.Н. Асимптотика движения фронта в задаче реакция-диффузия-адвекция // ЖВМиМФ. 2014. Т. 54. № 10. С. 35–49.
Nefedov N.N., Recke L., Schnieder K.R. Existence and Asymptotic Stability of Periodic Solutions with an Interior Layer of Reaction-Advection-Diffusion Equations // J. Mathematical Analysis and Applications. 2013. V. 405. P. 90–103.
Nefedov N. Comparison Principle for Reaction-Diffusion-Advection Problems with Boundary and Internal Layers // Lecture Notes in Computer Science. 2013. V. 8236. P. 62–72.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал