Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 76-79
МЕТОД ДВОЙНОГО ПОТЕНЦИАЛА ДЛЯ МОДЕЛИРОВАНИЯ ВНУТРЕННЕГО ТЕЧЕНИЯ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
С. В. Поляков 1, Т. А. Кудряшова 1, *, Н. И. Тарасов 1
1 Федеральный исследовательский центр
Институт прикладной математики им. М.В. Келдыша Российской академии наук
Москва, Россия
* E-mail: kudryashova@imamod.ru
Поступила в редакцию 22.06.2020
После доработки 22.06.2020
Принята к публикации 29.06.2020
Аннотация
Рассматривается проблема численного моделирования процессов очистки воды от примесей железа. Задача очистки актуальна для многих промышленных приложений, включая разработку новых способов и приборов очистки с целью приготовления ультрачистой воды. Проведенное математическое исследование связано с расчетами водного потока и переноса загрязняющих примесей в системе очистки в условиях реальной геометрии. В работе предложен новый численный подход к решению задачи, получены соответствующие расчетные данные. Анализ результатов показал, что они хорошо согласуются с результатами вычислений с использованием пакета ANSYS CFD.
Расчет внутреннего течения вязкой несжимаемой жидкости является важной задачей динамики сплошных сред. Такие расчеты широко применяются при решении многих прикладных задач. Примером такого применения служит проблема очистки водной среды от примесей тяжелых металлов электромагнитным способом. Для моделирования процесса очистки в этом случае применяется гидродинамическая модель на основе уравнений Навье–Стокса, дополненная уравнениями электростатики и конвекции-диффузии. Цель решения – получение распределения поля скоростей водной среды и расчет эволюции распространения примесей при управлении магнитным полем. В случае плоской или аксиально-симметричной геометрии гидродинамическая часть задачи решается в переменных функция тока – вихрь [1, 2]. Это позволяет избежать известных недостатков постановки в естественных переменных (скорость–давление) [3]. Также данная методика позволяет уменьшить число зависимых переменных: вместо двух координат скорости и функции давления здесь имеем две скалярные переменные. Во многих источниках отмечается отсутствие эффективного обобщения подобного метода на трехмерный случай. Однако это возможно [3] и достигается путем введения векторного потенциала и вектора вихря. При этом нетривиальным становится постановка граничных условий для векторного потенциала, которые оказывают определяющее влияние на результирующий вид потока [3]. Для преодоления проблемы постановки граничных условий при расчетах внутреннего течения несжимаемой жидкости в работах [4–6] был разработан метод двойного потенциала, который применяется и в данной работе.
Для моделирования течения вязкой несжимаемой жидкости будем основываться на системе уравнений Навье–Стокса и условии несжимаемости [7], в безразмерной постановке имеющих следующий вид:
(1)
$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \left( {{\mathbf{u}},\nabla } \right){\mathbf{u}} = \frac{1}{{\operatorname{Re} }}\Delta {\mathbf{u}} - \nabla p,$Cистема уравнений (1), (2) дополняется соответствующими граничными и начальными условиями.
Далее по методикам [3–6] производится переход к переменным (A, ${\varphi }$, ${\mathbf{\omega }}$), где A – векторный потенциал, ${\varphi }$ – скалярный потенциал, ${\mathbf{\omega }}$ – завихренность. Итоговая постановка задачи моделирования течения методом двойного потенциала представляется уравнениями и условиями:
(4)
$\frac{{\partial {\mathbf{\omega }}}}{{\partial t}} + \left( {{\mathbf{u}},\nabla } \right){\mathbf{\omega }} - \left( {{\mathbf{\omega }},\nabla } \right){\mathbf{u}} = \frac{1}{{\operatorname{Re} }}\Delta {\mathbf{\omega }},$(7)
${{A}_{{\tau }}} = \frac{{\partial {{A}_{n}}}}{{\partial {\mathbf{n}}}} = 0\quad {\text{на}}\quad ~\delta \Omega ,$(8)
$\frac{{\partial {\varphi }}}{{\partial n}} = \left( {{{{\left. u \right|}}_{{~\delta \Omega }}},n} \right)\quad {\text{на}}\quad ~\delta \Omega ,$(9)
${\mathbf{\omega }} = {\text{rot}}\left( {{{{\left. {\mathbf{u}} \right|}}_{{{\delta \Omega }}}}} \right)\quad {\text{на}}\quad ~\delta \Omega ,$(10)
${\mathbf{\omega }} = {\text{rot}}\left( {{{{\left. {\mathbf{u}} \right|}}_{{t = 0}}}} \right)\quad {\text{при}}\quad ~t = 0.$При моделировании двумерного потока ненулевым остается только z-составляющая вихря и, как следствие, векторного потенциала. Тогда, опуская обозначение координатной составляющей, уравнения (3), (4) принимают вид
(12)
$\frac{{\partial {\omega }}}{{\partial t}} + \left( {{\mathbf{u}},\nabla } \right){\omega } = \frac{1}{{\operatorname{Re} }}\Delta {\omega }.$Выражения для компонент вектора скорости принимают вид
(13)
${{u}_{x}} = \frac{{\partial A}}{{\partial y}} - \frac{{\partial {\varphi }}}{{\partial x}},\quad {{u}_{y}} = - \frac{{\partial A}}{{\partial x}} - \frac{{\partial {\varphi }}}{{\partial y}}.$Граничные условия (7) и (9) и начальные условия (10) принимают вид
(15)
$\omega = \frac{{\partial {{{\left. {{{u}_{y}}} \right|}}_{{{\delta \Omega }}}}}}{{\partial x}} - \frac{{\partial {{{\left. {{{u}_{x}}} \right|}}_{{{\delta \Omega }}}}}}{{\partial y}}\quad {\text{на}}\quad ~\delta \Omega ,$В итоге при решении задачи в плоской двумерной постановке используются уравнения (6), (11)–(13) с граничными условиями (8), (14), (15) и начальным условием (16).
Основное преимущество сформулированного выше метода двойного потенциала для расчета внутренних течений вязкой несжимаемой жидкости состоит в гарантированном выполнении условия (2), отсутствии переменной давления и простоте задания граничных условий на векторный потенциал.
Для реализации метода двойного потенциала была разработана оригинальная численная схема. Схема основана на методе конечных объемов, в качестве которых выступают ячейки сетки. В качестве сеток в трехмерном случае могут выступать как декартовы структурированные сетки, так и сетки, состоящие из многогранников с числом вершин от четырех до восьми. В двумерном варианте также могут использоваться декартовы сетки и сетки, состоящие из многоугольников с числом вершин от трех до шести. Для аппроксимации пространственных операторов типа конвекция–диффузия применяется экспоненциальное преобразование вектора потока. Построенная схема реализует метод двойного потенциала в трехмерном случае, а также его следствие в двумерной постановке.
В качестве примера приведем следующий расчет. Рассмотрим геометрию расчетной области, в двухмерном случае изображенную на рис. 1, направление потока схематично указано стрелками. На входном отверстии задано течение Пуазейля, на стенках – условие прилипания, а на выходе – мягкое граничное условие.
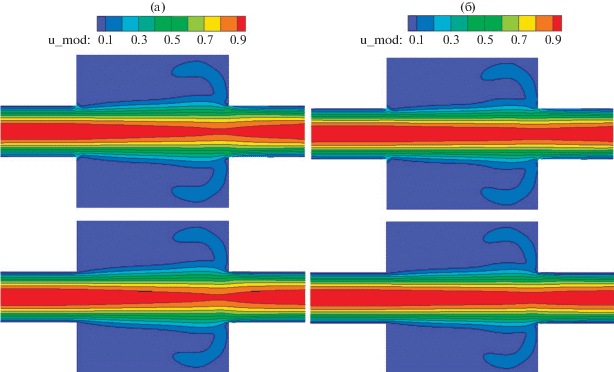
Для чисел Re = 10, 100, 300, 500 были получены распределения модуля скорости посредством описанного метода и Ansys Fluent, изображенные на рис. 2, 3, показывающие высокую степень согласованности результатов, различие не превышает 1%.
Рис. 2.
Распределение модуля скорости для Re = 10 (а) и Re = 100 (б), рассчитанное методом двойного потенциала (сверху) и с помощью Ansys Fluent (снизу).
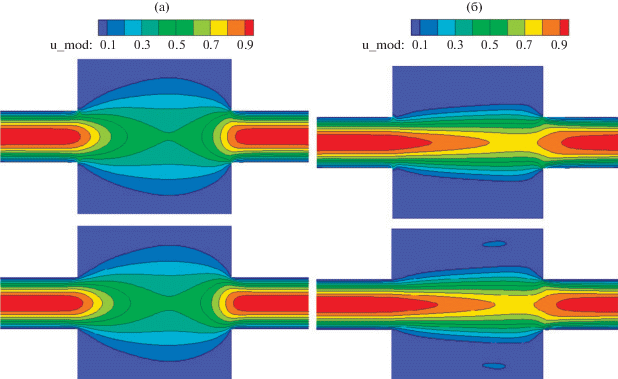
Рис. 3.
Распределение модуля скорости для Re = 300 (а) и Re = 500 (б), рассчитанное методом двойного потенциала (сверху) и с помощью Ansys Fluent (снизу).
Расчеты производились на декартовой сетке, содержащей 6912 элементов. Шаг по времени принимался равным 1.08503е-4. Стационарное состояние потока установилось спустя 66 300 для Re = 10, 212 500 для Re = 100, 439 600 для Re = 300, 681 100 для Re = 500 временных шагов.
В заключение отметим, что в рамках метода двойного потенциала нами предложена новая численная методика решения уравнений типа конвекция–диффузия для расчета завихренности, которая обладает гарантированной устойчивостью. Данная методика обобщается на случай использования конечно-объемных схем на нерегулярных сетках достаточно общего вида. С практической точки зрения методика в целом позволяет решать прикладные задачи экологии, например, задачи очистки водной среды от примесей тяжелых металлов.
Список литературы
Кудряшова Т.А., Поляков С.В., Пузырьков Д.В., Тарасов Н.И. Математическое моделирование процессов очистки воды от примесей железа. М.: РАН, 2017. 17 с.
Поляков С.В., Кудряшова Т.А., Карамзин Ю.Н., Тарасов Н.И. Mathematical Modelling of Water Treatment Processes // Mathematica Montisnigri. 2017. V. XL. P. 110–126.
Роуч П. Вычислительная гидродинамика. М.: Мир, 1980. 618 с.
Richardson S.M., Cornish A.R. Solution of Three-Dimentional Incompressible Flow Problens // J. Fluid Mech. 1977. V. 82. Pt 2. P. 309–319.
Richardson S.M. Numerical solution of the three-dimensional Navier–Stokes equations. Doctoral dissertation. Department of Chemical Engineering and Chemical Technology, Imperial College of Science and Technology, London, 1976.
Gegg S.G. A dual-potential formulation of the Navier-Stokes equations. 1989. Retrospective Theses and Dissertations. 9040. URL: https://lib.dr.iastate.edu/rtd/9040
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Гидродинамика. 3-е изд., испр. М.: Наука, Гл. ред. физ.-мат. лит, 1986. 736 с.
Eymard R., Gallouet T.R., Herbin R. The finite volume method. Handbook of Numerical Analysis, Amsterdam, North Holland. 2000. V. 7. P. 713–1020.
Поляков С.В. Экспоненциальные разностные схемы для уравнения конвекции-диффузии // Mathematica Montisnigri. 2012. V. XXVI (2013). P. 29–44.
Kudryashova T., Polyakov S., Tarasov N. Application of the Double Potential Method to Simulate Incompressible Viscous Flows. In: Rodrigues J. et al. (eds.) Computational Science – ICCS 2019. ICCS 2019. Lecture Notes in Computer Science. V. 11539. Springer, Cham.
Samarski A.A., Nikolaev E.S. Methods for the Solution of Grid Equations. M.: Nauka, 1978.
Matyushin P.V. Evolution of the diffusion-induced flow over a disk, submerged in a stratified viscous fluid // Mathematical Modeling. 2018. V. 30 (11). P. 44–58.
Koleshko S.B., Lapin Yu.V., Chumakov Yu.S. Turbulent Free-Convection Boundary Layer on a Vertical Heated Plate: Regularities of the Temperature Layer // High Temperature. 2005. V. 43 (3). P. 429–440.
Gushchin V.A., Matyushin P.V. Modeling and investigation of stratified fluid flows around finite bodies // Comput. Math. Math. Phys. 2016. V. 56 (6). P. 1034–1047.
Chorin A.J. A Numerical Method for Solving Incompressible Viscous Flow Problems // J. Computational Physics. 1997. V. 135. P. 118–125.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления