Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 64-67
МОДЕЛИРОВАНИЕ ГАЗОДИНАМИЧЕСКИХ ТЕЧЕНИЙ НА ГИБРИДНЫХ ЛОКАЛЬНО АДАПТИВНЫХ СЕТКАХ
1 Федеральный исследовательский центр
Институт прикладной математики им. М.В. Келдыша Российской академии наук
Москва, Россия
* E-mail: ssoukov@gmail.com
Поступила в редакцию 27.05.2019
После доработки 07.06.2020
Принята к публикации 29.06.2020
Аннотация
Представлен алгоритм численного моделирования уравнений Навье–Стокса на неструктурированных гибридных сетках с использованием метода локальной адаптации сеточной топологии к особенностям решения. Приводятся результаты расчета сверхзвукового течения вблизи поверхности сферы.
На сегодняшний день одним из распространенных подходов к дискретизации областей с произвольной формой границ для численного моделирования задач газовой динамики является генерация гибридных (смешанных) сеток. Такие сетки включают в себя структурированные и неструктурированные блоки с элементами различных типов. Для повышения качества результатов могут применяться методы адаптации [1–4], которые реализуют процедуру локального перестроения сеточной топологии с учетом структуры моделируемого течения. Адаптивная сетка сгущается к особенностям решения (расположение и форма поверхностей ударных волн, вихрей и т.д.) и, наоборот, шаг дискретизации увеличивается в области прохождения невозмущенного потока. В настоящей работе описан предложенный автором алгоритм численного моделирования газодинамических течений на локально адаптивных сетках, состоящих из тетраэдров, призм, пирамид и гексаэдров.
АЛГОРИТМ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ И СЕТОЧНАЯ АДАПТАЦИЯ
В качестве математической модели рассматривается система уравнений Навье–Стокса для вязкого сжимаемого теплопроводного газа, записанная в виде законов сохранения. Численный алгоритм моделирования течений представляет собой модификацию конечно-объемного метода повышенного порядка точности с линейной реконструкцией переменных внутри расчетных ячеек и определением их значений в центрах масс [5, 6].
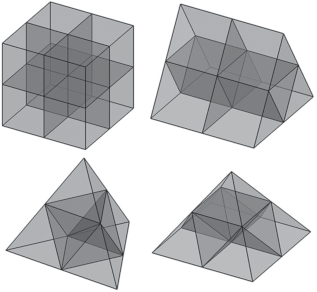
Механизм адаптации сетки состоит в иерархическом изотропном дроблении и объединении элементов (рис. 1).После измельчения гексаэдров, призм и тетраэдров образуется по восемь многогранников того же типа. Декомпозиция четырехугольной пирамиды состоит из шести пирамид и четырех тетраэдров.
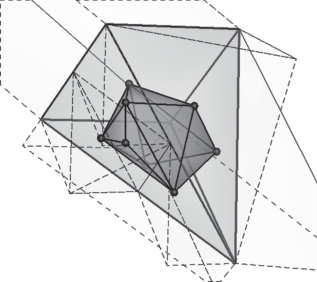
В вычислениях на адаптивных сетках для определения полиномиальных коэффициентов вводятся фиктивные контрольные объемы. Их вершины находятся в точках пересечения отрезков, соединяющих центры соседних расчетных ячеек, с плоскостями соответствующих граней. Объем фиктивной ячейки ограничивается триангуляцией выпуклой оболочки ее вершин. Значения переменных в вершинах и центрах граней фиктивной ячейки вычисляются линейной интерполяцией на отрезках и треугольниках. На рис. 2 показан пример фиктивного контрольного объема для пирамиды, которая граничит с четырьмя элементами (два тетраэдра, гексаэдр и призма) одинакового с ней уровня иерархии и четырьмя тетраэдрами нижнего уровня.
Решение о дроблении и объединении многогранников принимается после анализа распределения значений критериев адаптации ${{\phi }_{{cell}}}$ в расчетных ячейках. Выбор критерия или их комбинаций учитывает структуру моделируемого течения. Правило составления множества перестраиваемых элементов в общем виде описывается выражением
Границы интервала $\left( {{{\phi }_{{{\text{min}}}}};{{\phi }_{{{\text{max}}}}}} \right)$ задаются таким образом, чтобы в результате адаптации повысить точность разрешения особенностей течения, одновременно сохранив число расчетных ячеек в заданных пределах. С целью исключения резких перепадов между размерами элементов топология сетки всегда удовлетворяет условию, когда соседние расчетные ячейки отличаются не более чем на один уровень в иерархии.
Для определения значений газодинамических переменных в центрах масс дочерних ячеек используется полиномиальная реконструкция на родительском элементе. В случае их обратного слияния значение в центре родительского многогранника вычисляется осреднением по вложенным контрольным объемам.
Описанный алгоритм программно реализован как последовательное приложение для систем с многоядерными процессорами. Процедуры обработки сеточной топологии выделены в отдельную библиотеку подпрограмм.
ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Оценка корректности численного алгоритма и процедур сеточной адаптации проводилась на примере моделирования стационарного сверхзвукового обтекания сферы единичного диаметра. Параметры набегающего потока задавались числом Маха ${{M}_{\infty }} = 2$ и числом Рейнольдса ${\text{R}}{{{\text{e}}}_{\infty }}$ = 300. Проведено сравнение полученных характеристик течения с результатами расчета аналогичной задачи на структурированной сетке, опубликованными в [7].
Вычислительный эксперимент включает последовательный расчет задачи сначала на грубой конформной сетке (MI) и затем на двух локально адаптивных сетках (MA и MA2). Сетка MA адаптируется к решению на сетке MI. Сетка MA2 перестраивается в соответствии с результатом расчета на сетке MA. Расчет на каждой из сеток продолжается до установления стационарной картины течения.
Маркировка перестраиваемых элементов происходит путем сравнения значений трех критериев адаптации, учитывающих абсолютную величину градиента давления ($\phi _{{cell}}^{0} = \left| {\nabla p} \right|{{h}_{{cell}}}$), градиента модуля скорости ($\phi _{{cell}}^{1} = \left| {\nabla \left| {\mathbf{u}} \right|} \right|$) и модуль завихренности ($\phi _{{cell}}^{2} = \left| {\nabla \times {\mathbf{u}}} \right|{{h}_{{cell}}}$). Коэффициент ${{h}_{{cell}}}$ равен минимальной высоте элемента. Пороговые значения $\phi _{{{\text{min}}}}^{i}$ и $\phi _{{{\text{max}}}}^{i}$ подобраны экспериментально. Кроме того, процедура адаптации предусматривает преобразование элементов, находящихся вблизи изоповерхности локального числа Маха (M = 1) и границы рециркуляционной зоны.
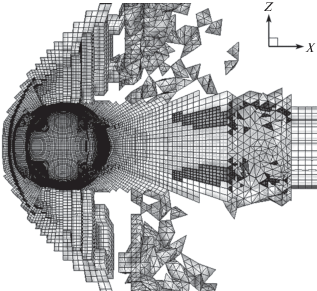
Исходная сетка MI объединяет 54 сеточных блока и суммарно содержит 268 633 ячейки. Область пограничного слоя заполнена гексаэдрами и призмами. Далее в окрестности сферы чередуются различные типы сеточных ячеек. На выходе к внешним границам расчетной области расположены тетраэдральный и гексаэдральный блоки (рис. 3).
Глубина измельчения сетки MA (577 386 расчетных ячеек) ограничивается первым уровнем разбиения. Иерархическая структура сетки MA2 (640 772 расчетных ячейки) включает элементы первого и второго уровня вложенности. В обоих случаях среди расчетных ячеек каждого уровня присутствуют многогранники всех типов. Зона адаптации содержит элементы из области разрешения пограничного слоя, а ее поверхность пересекает границы сеточных блоков (рис. 4).
Определенные по итогам вычислительного эксперимента параметры течения приведены в таб. 1. На фоне качественного совпадения результатов видно, что адаптация сеточной топологии повышает точность определения контрольных характеристик.
Таблица 1
| Расчетная сетка | MI | MA | MA2 | Работа [7] |
|---|---|---|---|---|
| Коэффициент лобового сопротивления | 1.360 | 1.400 | 1.395 | 1.385 |
| Расстояние до отошедшей ударной волны | 0.220 | 0.215 | 0.210 | 0.200 |
| Длина рециркуляционной зоны | 0.285 | 0.350 | 0.365 | 0.375 |
| Угол отрыва | 155.2 | 152.1 | 150.8 | 149.9 |
Расчет задачи на сетке MI с адаптацией под решение и продолжением вычислений на сетке MA занимает в 2.5 раза меньше процессорного времени по сравнению с расчетом на равномерно измельченной во всей области стартовой сетке.
ЗАКЛЮЧЕНИЕ
В работе представлен алгоритм численного моделирования уравнений Навье–Стокса на локально адаптивных гибридных сетках с элементами четырех типов и пример расчета стационарного сверхзвукового течения с адаптацией сетки к особенностям решения. Дальнейшее развитие исследований предполагает разработку автоматизированной процедуры динамической адаптации сеточной топологии для моделирования нестационарных течений и создание параллельных версий алгоритмов.
Список литературы
Powell K., Roe P., Quirk J. Adaptive-Mesh Algorithms for Computational Fluid Dynamics / In: M.Y. Hussaini, A. Kumar, M.D. Salas (eds). Algorithmic Trends in Computational Fluid Dynamics. N.Y.: ICASE/NASA LaRC Series. Springer, 1993.
Antepara O., Lehmkuhl O., Chiva J., Borrell R. Parallel Adaptive Mesh Refinement Simulation of the Flow Around a Square Cylinder at Re = 22000 // Procedia Engineering. 2013. V. 61. P. 246–250. https://doi.org/10.1016/j.proeng.2013.08.011
Schwing A., Nompelis I., Candler G. Parallelization of unsteady adaptive mesh refinement for unstructured Navier-Stokes solvers / In: AIAA AVIATION 2014 -7th AIAA Theoretical Fluid Mechanics Conference. American Institute of Aeronautics and Astronautics Inc. 2014. https://doi.org/10.2514/6.2014-3080.
Morgan N., Waltz J. 3D level set methods for evolving fronts on tetrahedral meshes with adaptive mesh refinement // J. Computational Physics. 2017. V. 336. P. 492–512. https://doi.org/10.1016/j.jcp.2017.02.030
Soukov S., Gorobets A., Bogdanov P. Portable Solution for Modeling Compressible Flows on All Existing Hybrid Supercomputers // Math. Models Comput. Simul. 2018. V. 10. № 2. P. 135–144.
Gorobets A., Soukov S., Bogdanov P. Multilevel parallelization for simulating turbulent flows on most kinds of hybrid supercomputers // Computers and Fluids. 2018. V. 173. P. 171–177. https://doi.org/10.1016/j.compfluid.2018.03.011
Nagata T., Nonomura T., Takahashi S., Mizuno Y., Fukuda K. Investigation on subsonic to supersonic flow around a sphere at low Reynolds number of between 50 and 300 by direct numerical simulation // Physics of Fluids/ 2016. V. 28. 056101. https://doi.org/10.1063/1.4947244
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления