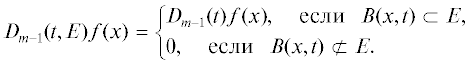Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 8-12

Интерполяция пространств функций положительной гладкости на области

Член-корреспондент РАН О. В. Бесов^1, *

¹ Математический институт им. В.А. Стеклова Российской академии наук
Москва, Россия

Поступила в редакцию 06.04.2020
После доработки 06.04.2020
Принята к публикации 22.10.2020

DOI: 10.31857/S2686954320060041

Аннотация

Дается описание интерполяционных пространств для пространств функций положительной гладкости на области с условием гибкого конуса.

Ключевые слова: регулярная область, пространства функций положительной гладкости, интерполяция, мультипликативные оценки

Дается описание интерполяционных пространств для пространств функций положительной гладкости на области G евклидова пространства ${{\mathbb{R}}^{n}}$, удовлетворяющей условию гибкого конуса. В качестве следствия получены мультипликативные оценки норм функций. Рассмотрения основаны на интегральных представлениях функции по гибкому конусу через ее локальные приближения многочленами и на оценках возникающих операторов свертки.

Пусть $\mathbb{N}$ – множество натуральных чисел; ${{\mathbb{N}}_{0}} = \mathbb{N} \cup \{ 0\} $; $n \in \mathbb{N}$; $n \geqslant 2;$ ${{\mathbb{R}}^{n}}$ – n-мерное евклидово пространство точек $x = ({{x}_{1}}, \ldots ,{{x}_{n}})$; все рассматриваемые функции локально суммируемы на области своего определения.

Определение 1. Область $G \subset {{\mathbb{R}}^{n}}$ будем называть областью с условием гибкого конуса, если при некоторых $T \in (0,1]$, $\kappa > 0$ для любого x ∈ G существует кусочно гладкий путь

(1)

$\gamma = {{\gamma }_{x}}{\text{:}}\,\,[0,T] \to G,\quad \gamma (0) = x,\quad {\text{|}}\gamma {\kern 1pt} '{\text{|}} \leqslant 1\;{\text{п}}.{\text{в}}.,$

такой, что

${\text{dist}}(\gamma (t),{{\mathbb{R}}^{n}}{\backslash }G) \geqslant \kappa t\quad {\text{при}}\quad 0 < t \leqslant T.$

Будем пользоваться следующими обозначениями. Везде далее символом G обозначается область в ${{\mathbb{R}}^{n}}$ с условием гибкого конуса, не совпадающая с ${{\mathbb{R}}^{n}}$, ${{G}_{\delta }} = \{ x \in G{\kern 1pt} :\;{\text{dist}}(x,\partial G) > \delta \} $ при δ > 0.

При $t > 0$, $E \subset {{\mathbb{R}}^{n}}$, $y \in {{\mathbb{R}}^{n}}$ положим

$\begin{gathered} y + tE: = \{ x{\kern 1pt} :\;x = y + tz,\;z \in E\} , \\ B(x,t): = \{ y{\kern 1pt} :\;{\text{|}}y - x{\text{|}} < t\} = x + B(0,t), \\ \end{gathered} $

χ – индикатор шара $B(0,1)$,

${\text{||}}\varphi \,{\text{|}}\,L_{{p,s}}^{*}{\text{||}}$ = = ${{\left\{ {\int\limits_0^T {{{{({{t}^{{ - s}}}\varphi (t))}}^{p}}\frac{{dt}}{t}} } \right\}}^{{1/p}}}$ при $1 \leqslant p < \infty ,$ ${\text{||}}\varphi \,{\text{|}}\,L_{{\infty ,s}}^{*}{\text{||}}$ = esssup|t^–sφ(t)|, ${\text{||}}\varphi \,{\text{|}}\,L_{p}^{*}{\text{||}} = {\text{||}}\varphi \,{\text{|}}\,L_{{p,0}}^{*}{\text{||}}$.

При $1 \leqslant p < \infty $ ${{L}_{p}}(G)$ – лебегово пространство определенных на открытом множестве $G \subset {{\mathbb{R}}^{n}}$ функций с нормой ${\text{||}}f\,{\text{|}}\,{{L}_{p}}(G){\text{||}} = {{\left( {\int\limits_G {{\text{|}}f(x){{{\text{|}}}^{p}}dx} } \right)}^{{1/p}}},$ L_p = = ${{L}_{p}}({{\mathbb{R}}^{n}})$. Все рассматриваемые функции f и производные D^αf локально суммируемы на области своего определения.

Символом $W_{p}^{s}(G)$ при $s \in \mathbb{N}$ будем обозначать пространство Соболева с нормой

$\begin{gathered} \left\| {f\,{\text{|}}\,W_{p}^{s}(G)} \right\| = \left\| {f\,{\text{|}}\,{{L}_{p}}(G)} \right\| + \sum\limits_{|\alpha | = s} \,\left\| {{{D}^{\alpha }}f\,{\text{|}}\,{{L}_{p}}(G)} \right\|, \\ W_{p}^{0}(G) = {{L}_{p}}(G). \\ \end{gathered} $

При $x,a \in {{\mathbb{R}}^{n}}$, t > 0 для числовой функции f положим ${{\tau }_{a}}f(x) = f(x + a)$, ${{\sigma }_{t}}f(x) = f(tx).$ Символом ${{\mathbb{P}}_{{m - 1}}}$ обозначим линейное пространство многочленов вида $\sum\limits_{|\alpha | \leqslant m - 1} {{{c}_{\alpha }}{{x}^{\alpha }}} $. Пусть $\pi = {{\pi }^{{m - 1}}}$: $L({{B}_{0}}) \to L({{B}_{0}})$ – некоторый проектор на ${{\mathbb{P}}_{{m - 1}}}$,

${{\pi }_{{a,t}}} = \tau _{a}^{{ - 1}} \circ \sigma _{t}^{{ - 1}} \circ \pi \circ {{\sigma }_{t}} \circ {{\tau }_{a}},$

${{D}_{{m - 1}}}(t)f(x) = {{t}^{{ - n}}}\left\| {f - {{\pi }_{{x,t}}}f\,{\text{|}}\,L(B(x,t))} \right\|.$

При $E \subset {{\mathbb{R}}^{n}}$ положим

Замечание 1. Локальное приближение || f – ${{\pi }_{{x,t}}}f\,{\text{|}}\,L(B(x,t)){\text{||}}$ функции f проекционным многочленом из ${{\mathbb{P}}_{{m - 1}}}$ эквивалентно ее наилучшему приближению в $L(B(x,t))$ с помощью многочленов из ${{\mathbb{P}}_{{m - 1}}}$.

Определение 2. При $1 \leqslant p,$ $q \leqslant \infty $, $m \in \mathbb{N}$, $0 < s < m$ символами $B_{{p,q}}^{s}(G)$, $L_{{p,q}}^{s}(G)$ обозначим банаховы пространства определенных на G функций с конечными нормами соответственно:

(2)

${\text{||}}f\,{\text{|}}\,B_{{p,q}}^{s}(G){\text{||}} = {\text{||}}f\,{\text{|}}\,{{L}_{p}}({{G}_{\delta }}){\text{||}}\; + \;{\text{||}}f\,{\text{|}}\,b_{{p,q}}^{s}(G){\text{||}},$

(3)

${\text{||}}f\,{\text{|}}\,L_{{p,q}}^{s}(G){\text{||}} = {\text{||}}f\,{\text{|}}\,{{L}_{p}}({{G}_{\delta }}){\text{||}}\; + \;{\text{||}}f\,{\text{|}}\,l_{{p,q}}^{s}(G){\text{||}},$

где $\delta \in (0,T)$ достаточно мало и в случае $p,q < \infty $

${\text{||}}f\,{\text{|}}\,b_{{p,q}}^{s}(G){\text{||}} = {{\left\{ {\int\limits_0^T \,{{{\left( {\int\limits_G \,{{{[{{D}_{{m - 1}}}(t,G)f(x)]}}^{p}}dx} \right)}}^{{q/p}}}{{t}^{{ - sq - 1}}}dt} \right\}}^{{1/q}}},$

${\text{||}}f\,{\text{|}}\,l_{{p,q}}^{s}(G){\text{||}} = {{\left\{ {\int\limits_G \,{{{\left( {\int\limits_0^T \,{{{[{{D}_{{m - 1}}}(t,G)f(x)]}}^{q}}{{t}^{{ - sq - 1}}}dt} \right)}}^{{p/q}}}dx} \right\}}^{{1/p}}},$

с обычной модификацией при $p = \infty $ или $q = \infty .$

Замечание 2. Эквивалентные нормы в пространствах $L_{{p,q}}^{s}(G)$, $B_{{p,q}}^{s}(G)$ можно задать через разности функций вместо локальных приближений, см. [1]. Доказательство эквивалентности имеется также в [4]. Отметим еще, что при натуральных s и q = 2 пространства $L_{{p,2}}^{s}(G)$ совпадают с пространствами Соболева $W_{p}^{s}(G)$, см. [1].

Через ${{({{A}_{0}},{{A}_{1}})}_{{\theta ,r}}}$, ${{({{A}_{0}},{{A}_{1}})}_{{[\theta ]}}}$ будем обозначать интерполяционные пространства между банаховыми пространствами A₀ и A₁, получаемые соответственно методами вещественной и комплексной интерполяции. Следующая теорема хорошо известна в случае $G = {{\mathbb{R}}^{n}}$, см. [2, 3]. Для области $G$ с “усиленным условием конуса” она приведена в [1].

Теорема 1. Пусть $G \subset {{\mathbb{R}}^{n}}$ – область с условием гибкого конуса,

$\begin{gathered} {{s}_{0}},{{s}_{1}} \in (0,\infty ),\quad r \in [1,\infty ], \\ {{p}_{0}},{{p}_{1}},p,{{q}_{0}},{{q}_{1}},q \in [1,\infty ],\quad 0 < \theta < 1, \\ \end{gathered} $

$\begin{gathered} s = (1 - \theta ){{s}_{0}} + \theta {{s}_{1}}, \\ \frac{1}{p} = \frac{{1 - \theta }}{{{{p}_{0}}}} + \frac{\theta }{{{{p}_{1}}}},\quad \frac{1}{q} = \frac{{1 - \theta }}{{{{q}_{0}}}} + \frac{\theta }{{{{q}_{1}}}}. \\ \end{gathered} $

Тогда при указанных в формулах дополнительных ограничениях справедливы интерполяционные равенства:

(4)

$\begin{gathered} {{(B_{{p,{{q}_{0}}}}^{{{{s}_{0}}}}(G),B_{{p,{{q}_{1}}}}^{{{{s}_{1}}}}(G))}_{{\theta ,r}}} = B_{{p,r}}^{s}(G) \\ ({{s}_{0}} \ne {{s}_{1}}\;\;или\;\;r = q), \\ \end{gathered} $

(5)

$\begin{gathered} {{(B_{{{{p}_{0}},{{q}_{0}}}}^{{{{s}_{0}}}}(G),B_{{{{p}_{1}},{{q}_{1}}}}^{{{{s}_{1}}}}(G))}_{{\theta ,q}}} = B_{{p,q}}^{s}(G) \\ (p = q,{{q}_{0}},\;\;{{q}_{1}} < \infty ), \\ \end{gathered} $

(6)

${{(B_{{{{p}_{0}},{{q}_{0}}}}^{{{{s}_{0}}}}(G),B_{{{{p}_{1}},{{q}_{1}}}}^{{{{s}_{1}}}}(G))}_{{[\theta ]}}} = B_{{p,q}}^{s}(G)({{q}_{0}} < \infty ),$

(7)

$\begin{gathered} {{(W_{p}^{{{{s}_{0}}}}(G),W_{p}^{{{{s}_{1}}}}(G))}_{{\theta ,r}}} = B_{{p,r}}^{s}(G) \\ (верно\;и\;при\;\;0 \leqslant {{s}_{0}} < {{s}_{1}} < \infty ), \\ \end{gathered} $

а также при $1 < {{p}_{0}},{{p}_{1}},p,{{q}_{0}},{{q}_{1}},q < \infty $ следующие три равенства:

(8)

$\begin{gathered} {{(L_{{{{p}_{0}},{{q}_{0}}}}^{{{{s}_{0}}}}(G),L_{{{{p}_{1}},{{q}_{1}}}}^{{{{s}_{1}}}}(G))}_{{\theta ,p}}} = L_{{p,p}}^{s}(G) = B_{{p,p}}^{s}(G) \\ ({{s}_{0}} \ne {{s}_{1}}\;\;или\;\;p = q), \\ \end{gathered} $

(9)

${{(L_{{{{p}_{0}},q}}^{s}(G),L_{{{{p}_{1}},q}}^{s}(G))}_{{\theta ,p}}} = L_{{p,q}}^{s}(G),$

(10)

${{(L_{{{{p}_{0}},{{q}_{0}}}}^{{{{s}_{0}}}}(G),L_{{{{p}_{1}},{{q}_{1}}}}^{{{{s}_{1}}}}(G))}_{{[\theta ]}}} = L_{{p,q}}^{s}(G).$

Одно из свойств интерполяционных пространств состоит в оценке (см. [2, теорема 1.3.3])

$\begin{gathered} {\text{||}}a{\text{|}}{{{\text{|}}}_{{{{{({{A}_{0}},{{A}_{!}})}}_{{\theta ,r}}}}}} \leqslant {{C}_{{\theta ,r}}}{\text{||}}a{\text{||}}_{{{{A}_{0}}}}^{{1 - \theta }}{\text{||}}a{\text{||}}_{{{{A}_{1}}}}^{\theta }, \\ 0 < \theta < 1,\quad 1 \leqslant r \leqslant \infty . \\ \end{gathered} $

Поэтому из теоремы 1 вытекает

Следствие 1. При соотношениях параметров, указанных в теореме 1, справедливы мультипликативные оценки

$\left\| {f\,{\text{|}}\,B_{{p,r}}^{s}(G)} \right\| \leqslant C{{\left\| {f\,{\text{|}}\,B_{{{{p}_{0}},{{q}_{0}}}}^{{{{s}_{0}}}}(G)} \right\|}^{{1 - \theta }}}{{\left\| {f\,{\text{|}}\,B_{{{{p}_{1}},{{q}_{1}}}}^{{{{s}_{1}}}}(G)} \right\|}^{\theta }},$

$\left\| {f\,{\text{|}}\,L_{{p,r}}^{s}(G)} \right\| \leqslant C{{\left\| {f\,{\text{|}}\,L_{{{{p}_{0}},{{q}_{0}}}}^{{{{s}_{0}}}}(G)} \right\|}^{{1 - \theta }}}{{\left\| {f\,{\text{|}}\,L_{{{{p}_{1}},{{q}_{1}}}}^{{{{s}_{1}}}}(G)} \right\|}^{\theta }}.$

Эти мультипликативные оценки для области G менее общего вида являются следствием интерполяционной теоремы из [1].

Основой рассмотрений служит интегральное представление функции, являющееся аналогом интегральных представлений из [1]. Приведем его.

Пусть $\vartheta \in {{C}^{\infty }}(\mathbb{R}),$ $\vartheta (u) = 0$ при $u \leqslant - \delta ,$ $\vartheta (u) = 1$ при $u \geqslant \delta ,$ $\tau ,{{\tau }_{1}} \in \mathbb{R},$ $0 < \delta < \frac{\kappa }{3}\sqrt n ,$

(11)

$\begin{gathered} \omega (u,\tau ) = \frac{{{{d}^{k}}}}{{d{{u}^{k}}}}\left( {\frac{{{{u}^{{k - 1}}}}}{{(k - 1)!}}\vartheta (u - \tau )} \right), \\ {\text{так}}\;{\text{что}}\quad \int {\omega (u,\tau )du} = 1, \\ \xi (u,\tau ) = \frac{{{{u}^{k}}}}{{(k - 1)!}}\vartheta {\kern 1pt} '(u - \tau ) = u\eta (u,\tau ), \\ \end{gathered} $

(12)

$\begin{gathered} \zeta (u,\tau ,{{\tau }_{1}}) = \xi (u,\tau ) + \\ \, + (\tau - {{\tau }_{1}})\eta (u,\tau ),\xi ( \cdot ,\tau ),\eta ( \cdot ,\tau ),\zeta ( \cdot ,\tau ,{{\tau }_{1}}) \in C_{0}^{\infty }. \\ \end{gathered} $

При t > 0, $\tau = \tau (t)$

$\begin{gathered} \frac{\partial }{{\partial t}}\left[ {\frac{1}{t}\omega \left( {\frac{u}{t},\frac{\tau }{t}} \right)} \right] = - \frac{1}{{{{t}^{2}}}}\left[ {\frac{u}{t}\omega _{u}^{'}\left( {\frac{u}{t},\frac{\tau }{t}} \right) + \omega \left( {\frac{u}{t},\frac{\tau }{t}} \right)} \right] + \\ + \frac{1}{t}\omega _{\tau }^{'}\left( {\frac{u}{t},\frac{\tau }{t}} \right)\frac{d}{{dt}}\left( {\frac{\tau }{t}} \right). \\ \end{gathered} $

Заметим, что

$\begin{gathered} u\omega _{u}^{'}(u,\tau ) + \omega (u,\tau )) = u\frac{{{{\partial }^{{k + 1}}}}}{{\partial {{u}^{{k + 1}}}}}\left( {\frac{{{{u}^{{k - 1}}}}}{{(k - 1)!}}\vartheta (u - \tau )} \right) + \\ \, + \frac{{{{\partial }^{k}}}}{{\partial {{u}^{k}}}}\left( {\frac{{{{u}^{{k - 1}}}}}{{(k - 1)!}}\vartheta (u - \tau )} \right) = \frac{{{{\partial }^{{k + 1}}}}}{{\partial {{u}^{{k + 1}}}}}\left( {u\frac{{{{u}^{{k - 1}}}}}{{(k - 1)!}}\vartheta (u - \tau )} \right) - \\ \end{gathered} $

$\begin{gathered} \, - k\frac{{{{\partial }^{k}}}}{{\partial {{u}^{k}}}}\left( {\frac{{{{u}^{{k - 1}}}}}{{(k - 1)!}}\vartheta (u - \tau )} \right) = \\ \, = \frac{{{{\partial }^{k}}}}{{\partial {{u}^{k}}}}\left[ {\frac{{{{u}^{k}}}}{{(k - 1)!}}\vartheta '(u - \tau )} \right] = \frac{{{{\partial }^{k}}}}{{\partial {{u}^{k}}}}\xi (u,\tau ). \\ \end{gathered} $

Отсюда и из (12) имеем

(13)

$\begin{gathered} \frac{\partial }{{\partial t}}\left[ {\frac{1}{t}\omega \left( {\frac{u}{t},\frac{{\tau (t)}}{t}} \right)} \right] = \\ \, = - \frac{1}{{{{t}^{2}}}}\left[ {\xi _{u}^{{(k)}}\left( {\frac{u}{t},\frac{{\tau (t)}}{t}} \right) + \left( {\frac{{\tau (t)}}{t} - \tau {\kern 1pt} '(t)} \right)\eta _{u}^{{(k)}}\left( {\frac{u}{t},\frac{{\tau (t)}}{t}} \right)} \right] = \\ \, = - {{t}^{{ - 2}}}{{\zeta }^{{(k)}}}\left( {\frac{u}{t},\frac{{\tau (t)}}{t},\tau '(t)} \right), \\ \end{gathered} $

где ζ^(k) означает производную порядка k по первому аргументу.

Для $f \in L(G,{\text{loc}}),$ $0 < t \leqslant T$ введем усреднения

$\begin{gathered} {{{\tilde {f}}}_{t}}(y) = {{t}^{{ - 2n}}}\iint {\Omega \left( {\frac{z}{t}} \right)\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{y}}(t) - y}}{t}} \right)} \times \\ \, \times f(y + z + w)dzdw, \\ {{f}_{t}}(x) = {{t}^{{ - n}}}\int {\Omega \left( {\frac{y}{t}} \right){{{\tilde {f}}}_{t}}(x + y)dy} , \\ \end{gathered} $

где

$\begin{gathered} \Omega (y,z) = \prod\limits_{i = 1}^n \,\omega ({{y}_{i}},{{z}_{i}}),\quad \omega (u) = \omega (u,0), \\ \Omega (y) = \Omega (y,0),\quad \int {\Omega (y,z)dy} = 1. \\ \end{gathered} $

Легко убедиться, что ${{f}_{t}} \to f$ при $t \to 0 + 0$ в смысле сходимости в L(G, loc) и почти всюду. Имеем далее

$\begin{gathered} \frac{\partial }{{\partial t}}\left[ {{{t}^{{ - 3n}}}\Omega \left( {\frac{y}{t}} \right)\Omega \left( {\frac{z}{t}} \right)\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{{x + y}}}(t) - (x + y)}}{t}} \right)} \right] = \\ \, = {{t}^{{ - 1 - 3n}}}\sum\limits_{i = 1}^n \,\left[ {\Omega \left( {\frac{y}{t}} \right)\Omega \left( {\frac{z}{t}} \right)} \right. \times \\ \, \times D_{i}^{k}{{\Phi }_{i}}\left( {\frac{w}{t},\frac{{{{\gamma }_{{x + y}}}(t) - (x + y)}}{t},{{\gamma }_{{x + y}}}(t)} \right) + \\ \end{gathered} $

$\begin{gathered} \, + \Omega \left( {\frac{y}{t}} \right){{\Phi }_{i}}\left( {\frac{z}{t}} \right)D_{i}^{k}\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{{x + y}}}(t) - (x + y)}}{t}} \right) + \\ \, + \left. {{{\Phi }_{i}}\left( {\frac{y}{t}} \right)\Omega \left( {\frac{z}{t}} \right)D_{i}^{k}\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{{x + y}}}(t) - (x + y)}}{t}} \right)} \right], \\ \end{gathered} $

где ${{\Phi }_{i}}( \cdot ,y,z) \in C_{0}^{\infty }({{R}^{n}})$, ${{\Phi }_{i}}(y) = {{\Phi }_{i}}(y,0,0)$.

Применив формулу Ньютона–Лейбница на отрезке $[\varepsilon ,T]$, получим при $\varepsilon \to 0 + 0$

$f(x) = {{f}_{T}}(x) + \int\limits_0^T {\iiint {{{t}^{{ - 1 - 3n}}}}} \sum\limits_{i = 1}^n \,\left[ {\Omega \left( {\frac{y}{t}} \right)\Omega \left( {\frac{z}{t}} \right)} \right. \times $

(14)

$\begin{gathered} \, \times D_{i}^{k}{{\Phi }_{i}}\left( {\frac{w}{t},\frac{{{{\gamma }_{{x + y}}}(t) - (x + y)}}{t},\gamma _{{x + y}}^{'}(t)} \right) + \\ \, + \Omega \left( {\frac{y}{t}} \right){{\Phi }_{i}}\left( {\frac{z}{t}} \right)D_{i}^{k}\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{{x + y}}}(t) - (x + y)}}{t}} \right) + \\ \end{gathered} $

$\begin{gathered} \, + \left. {{{\Phi }_{i}}\left( {\frac{y}{t}} \right)\Omega \left( {\frac{z}{t}} \right)D_{i}^{k}\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{{x + y}}}(t) - (x + y)}}{t}} \right)} \right] \times \\ \, \times f(x + y + z + w)dydzdwdt, \\ \end{gathered} $

где равенство понимается в смысле сходимости в $L(G,{\text{loc}})$ и почти всюду. Здесь D_i означает производную по i-й координате первого векторного аргумента функции.

Запишем интегральное представление (8) в виде произведения двух операторов: $f(x) = \mathcal{R}\mathcal{S}f(x)$. Введем для этого некоторые обозначения.

Определение 3. Пусть $1 \leqslant p \leqslant \infty ,$ $1 \leqslant q \leqslant \infty ,$ s > 0. Пространством $L_{{q(s)}}^{*}({{L}_{p}})$ назовем банахово пространство наборов

$a = \{ {{a}_{0}},{{\{ {{a}_{{ji}}}\} }_{{1 \leqslant j \leqslant 3,\,1 \leqslant i \leqslant n}}}\} $

функций, где ${{a}_{0}} \in {{L}_{p}}(G)$, ${{a}_{{ji}}}$ – L_p-значные функции на (0, T], с нормой при q < ∞

$\begin{gathered} {\text{||}}a\,{\text{|}}\,L_{{q(s)}}^{*}({{L}_{p}}){\text{||}}: = {\text{||}}{{a}_{0}}\,{\text{|}}\,{{L}_{p}}{\text{||}} + \\ \, + \sum\limits_{j = 1}^3 \,\sum\limits_{i = 1}^n \,{{\left\{ {\int\limits_0^T \,{{t}^{{ - sq - 1}}}{\text{||}}{{a}_{{ji}}}( \cdot ,t)\,{\text{|}}\,{{L}_{p}}{\text{|}}{{{\text{|}}}^{q}}dt} \right\}}^{{1/q}}} \\ \end{gathered} $

с соответствующей модификацией при q = ∞.

Пространством ${{L}_{p}}(L_{{q(s)}}^{*})$ назовем банахово пространство наборов a = {a₀, ${{\{ {{a}_{{ji}}}\} }_{{1 \leqslant j \leqslant 3,\,\,1 \leqslant i \leqslant n}}}\} $ функций, где ${{a}_{0}} \in {{L}_{p}}$, ${{a}_{{ji}}}$ – ${{L}_{{q(s)}}}$-значные функции на ${{\mathbb{R}}^{n}}$, с нормой при q < ∞

$\begin{gathered} {\text{||}}a\,{\text{|}}\,L_{{q(s)}}^{ * }({{L}_{p}}){\text{||}} = {\text{||}}{{a}_{0}}\,{\text{|}}\,{{L}_{p}}{\text{||}} + \\ \, + \sum\limits_{j = 1}^3 \,\sum\limits_{i = 1}^n \,\left\| {{{{\left\{ {\int\limits_o^T \,{{t}^{{sq - 1}}}{\text{|}}{{a}_{{ji}}}( \cdot ,t){{{\text{|}}}^{q}}dt} \right\}}}^{{1/q}}}\,{\text{|}}\,{{L}_{p}}} \right\| \\ \end{gathered} $

с соответствующей модификацией при q = ∞.

Положим

(15)

$\mathcal{S}f = \{ {{\mathcal{S}}_{0}}f,{{\{ {{\mathcal{S}}_{{ji}}}f\} }_{{1 \leqslant j \leqslant 3,\,\,1 \leqslant i \leqslant n}}}\} \quad {\text{при}}\;\;f{\kern 1pt} :\;G \to {{\mathbb{R}}^{n}},$

где

$\begin{gathered} {{\mathcal{S}}_{0}}f(y) = {{T}^{{ - 3n}}}\iint {\Omega \left( {\frac{z}{T}} \right)\Omega \left( {\frac{w}{T},\frac{{{{\gamma }_{y}}(t) - y}}{T}} \right)} \times \\ \, \times f(y + z + w)dzdw,\quad y \in G, \\ \end{gathered} $

$\begin{gathered} {{\mathcal{S}}_{{1i}}}f(y,t) = \iint {{{t}^{{ - 2n}}}\Omega \left( {\frac{z}{t}} \right)D_{i}^{k}\Phi \left( {\frac{w}{t},\frac{{{{\gamma }_{y}}(t) - y}}{t},{{\gamma }_{y}}(t)} \right)} \times \\ \, \times f(y + z + w)dzdw,\quad y \in G,\quad 0 < t \leqslant T, \\ \end{gathered} $

$\begin{gathered} {{\mathcal{S}}_{{2i}}}f(y,t) = \iint {{{t}^{{ - 2n}}}\Phi \left( {\frac{z}{t}} \right)D_{i}^{k}\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{y}}(t) - y}}{t},{{\gamma }_{y}}(t)} \right)} \times \\ \, \times f(y + z + w)dzdw,\quad y \in G,\quad 0 < t \leqslant T, \\ \end{gathered} $

$\begin{gathered} {{\mathcal{S}}_{{3i}}}f(y,t) = \iint {{{t}^{{ - 2n}}}\Omega \left( {\frac{z}{t}} \right)D_{i}^{k}\Omega \left( {\frac{w}{t},\frac{{{{\gamma }_{y}}(t) - y}}{t},{{\gamma }_{y}}(t)} \right)} \times \\ \, \times f(y + z + w)dzdw,\quad y \in G,\quad 0 < t \leqslant T. \\ \end{gathered} $

Функции ${{\mathcal{S}}_{0}}f,\;{{\mathcal{S}}_{{ji}}}f$ определены на множествах, соответственно, $G,G \times (0,T]$. Будем считать их доопределенными нулем соответственно на ${{\mathbb{R}}^{n}}{\backslash }G$, $({{\mathbb{R}}^{n}}{\backslash }G)$ × (0, T].

При $a(x,t)$ = $\{ {{a}_{0}}(x),{{\{ {{a}_{{ji}}}(x,t)\} }_{{1 \leqslant j \leqslant 3,1 \leqslant i \leqslant n}}}\} ,$ $x \in {{\mathbb{R}}^{n}},$ $0 < t \leqslant T$, положим

$\mathcal{R}a(x) = {{\mathcal{R}}_{0}}{{a}_{0}}(x) + \sum\limits_{1 \leqslant j \leqslant 3,1 \leqslant i \leqslant n} \,{{\mathcal{R}}_{{ji}}}{{a}_{{ji}}}(x),$

(16)

$\begin{gathered} {{\mathcal{R}}_{0}}{{a}_{0}}(x) = \frac{1}{{{{T}^{n}}}}\int {\Omega \left( {\frac{y}{T}} \right){{a}_{0}}(x + y)dy} , \\ {{\mathcal{R}}_{{ji}}}{{a}_{{ji}}}(x) = \int {\int\limits_0^T {\frac{1}{{{{t}^{{1 + n}}}}}\Omega \left( {\frac{y}{t}} \right){{a}_{{ji}}}(x + y,t)dtdy} } \\ (j = 1,2), \\ \end{gathered} $

${{\mathcal{R}}_{{3i}}}{{a}_{{3i}}}(x) = \int {\int\limits_0^T {\frac{1}{{{{t}^{{1 + n}}}}}\Phi \left( {\frac{y}{t}} \right){{a}_{{3i}}}(x + y,t)dtdy} } .$

Тогда

(17)

$\begin{gathered} f(x) = {{\mathcal{R}}_{0}}{{\mathcal{S}}_{0}}f(x) + \sum\limits_{j = 1}^3 \,\sum\limits_{i = 1}^n \,{{\mathcal{R}}_{{ji}}}{{\mathcal{S}}_{{ji}}}f(x) = \\ \, = \mathcal{R}\mathcal{S}f(x)\quad {\text{при}}\quad x \in G. \\ \end{gathered} $

Лемма 1. Следующие операторы ограничены:

(18)

${{S}_{0}}{\kern 1pt} :\;{{L}_{p}}(G) \to {{L}_{p}},$

(19)

$\begin{gathered} {{\mathcal{S}}_{{ji}}}{\kern 1pt} :\;B_{{p,q}}^{s}(G) \to L_{{q(s)}}^{*}({{L}_{p}}), \\ L_{{p,q}}^{s}(G) \to {{L}_{p}}(L_{{q(s)}}^{*}),\quad {{L}_{p}}(G) \to {{L}_{p}}(L_{2}^{*}), \\ \end{gathered} $

(20)

${{\mathcal{R}}_{0}}{\kern 1pt} :\;{{L}_{p}} \to B_{{p,q}}^{s}(G),\quad {{L}_{p}} \to L_{{p,q}}^{s}(G),$

(21)

$\begin{gathered} {{\mathcal{R}}_{{ji}}}{\kern 1pt} :\;L_{{q(s)}}^{*}({{L}_{p}}) \to B_{{p,q}}^{s}(G), \\ {{L}_{p}}(L_{{q(s)}}^{*}) \to L_{{p,q}}^{s}(G),\quad {{L}_{p}}(L_{2}^{*}) \to {{L}_{p}}(G). \\ \end{gathered} $

Доказательство теоремы 1 с помощью теоремы о ретракции сводится к интерполяционным теоремам для весовых пространств банаховозначных последовательностей и пространств L_p банаховозначных функций. Эта схема применялась в случае $G = {{\mathbb{R}}^{n}}$, при этом операторы коретракции и ретракции строились с помощью гармонических разложений функции. В рассматриваемом случае такой способ невозможен. Коретракция и ретракция строятся здесь с помощью интегральных представлений функций.

Определение 4 (см. [2]). Банахово пространство Y называется ретрактом банахова пространства X, если существуют линейные непрерывные операторы $\mathcal{R}{\kern 1pt} :\;X \to Y$ (ретракция) и $\mathcal{S}$ (коретракция) такие, что I_Y = $\mathcal{R}\mathcal{S}{\kern 1pt} :\;Y \to Y$ является тождественным оператором.

Теорема 2. Пусть G – открытое множество с условием гибкого конуса. Пространства

$\begin{gathered} B_{{p,q}}^{s}(G)\,\,(1 \leqslant p,q \leqslant \infty ,s > 0), \\ L_{{p,q}}^{s}(G)\,\,(1 < p,q < \infty ,s > 0),\quad {{L}_{p}}(G)\,\,(1 < p < \infty ) \\ \end{gathered} $

являются ретрактами соответственно пространств

$L_{{q(s)}}^{*}({{L}_{p}}),\;\;{{L}_{p}}(L_{{q(s)}}^{*}),\;\;{{L}_{p}}(L_{2}^{*}).$

При этом операторы $\mathcal{S}$ (коретракции) и $\mathcal{R}$ (ретракции) задаются формулами (15), (16).

Теорема 3. Пусть ${{A}_{0}},{{A}_{1}},A$ – банаховы пространства,

$\begin{gathered} {{s}_{0}},{{s}_{1}} \in (0,\infty ), \\ {{p}_{0}},{{p}_{1}},p,{{q}_{0}},{{q}_{1}},q,r \in [1,\infty ],\quad 0 < \theta < 1, \\ \end{gathered} $

Тогда при указанных в формулах дополнительных ограничениях справедливы интерполяционные равенства:

(22)

$\begin{gathered} {{(L_{{{{q}_{0}}({{s}_{0}})}}^{*}(A),L_{{{{q}_{1}}({{s}_{1}})}}^{*}(A))}_{{\theta ,r}}} = L_{{r(s)}}^{*}(A) \\ ({{s}_{0}} \ne {{s}_{1}}\;\;{\text{или}}\;\;r = q), \\ \end{gathered} $

(23)

$\begin{gathered} {{(L_{{{{q}_{0}}({{s}_{0}})}}^{*}({{A}_{0}}),L_{{{{q}_{1}}({{s}_{1}})}}^{*}({{A}_{1}}))}_{{\theta ,q}}} = {{L}_{{q(s)}}}({{({{A}_{0}},{{A}_{1}})}_{{\theta ,q}}}) \\ ({{q}_{0}},{{q}_{1}} < \infty ), \\ \end{gathered} $

(24)

$\begin{gathered} {{(L_{{{{q}_{0}}({{s}_{0}})}}^{*}({{A}_{0}}),L_{{{{q}_{1}}({{s}_{1}})}}^{*}({{A}_{1}}))}_{{[\theta ]}}} = L_{{q(s)}}^{*}({{({{A}_{0}},{{A}_{1}})}_{{[\theta ]}}}) \\ ({{q}_{0}} < \infty ,\;\;{{q}_{1}} \leqslant \infty ), \\ \end{gathered} $

(25)

${{({{L}_{{{{p}_{0}}}}}({{A}_{0}}),{{L}_{{{{p}_{1}}}}}({{A}_{1}}))}_{{\theta ,p}}} = {{L}_{p}}({{({{A}_{0}},{{A}_{1}})}_{{\theta ,p}}})\,\,\,({{p}_{0}},{{p}_{1}}\, < \,\infty ),$

(26)

${{({{L}_{{{{p}_{0}}}}}({{A}_{0}}),{{L}_{{{{p}_{1}}}}}({{A}_{1}}))}_{{[\theta ]}}} = {{L}_{p}}({{({{A}_{0}},{{A}_{1}})}_{{[\theta ]}}})\,\,\,({{p}_{0}},{{p}_{1}} < \infty ).$

Доказательство. Доказательства равенств (25), (26) приведены в [2, 3]. Равенства (22)–(24), вероятно, также известны. Отметим, что равенство (22) можно доказать, повторяя доказательство теоремы 1.18.2 из [2], установленной для пространств векторнозначных последовательностей. Доказательство равенств (23), (24) сводится к теореме 1.18.2 из [2] (об интерполяции пространств векторнозначных последовательностей) с помощью следующей перенормировки:

$\begin{gathered} {\text{||}}f\,{\text{|}}\,L_{{q(s)}}^{*}(A){\text{|}}{{{\text{|}}}^{q}} = \sum\limits_{k = {{k}_{0}}}^\infty \,\int\limits_{{{2}^{{ - k}}}}^{{{2}^{{ - k + 1}}}} \,{{({{t}^{s}}{\text{||}}f(t)\,{\text{|}}\,A{\text{||}})}^{q}}\frac{{dt}}{t} \times \\ \, \times \sum\limits_{k = {{k}_{0}}}^\infty \,{{2}^{{ - k(sq - 1)}}}{\text{||}}{{f}_{k}}\,{\text{|}}\,{{L}_{q}}(A){\text{|}}{{{\text{|}}}^{q}} = {\text{||}}\{ {{f}_{k}}\} \,{\text{|}}\,l_{q}^{{s - 1/q}}({{L}_{q}}(A)){\text{|}}{{{\text{|}}}^{q}}. \\ \end{gathered} $

Доказательство равенств (4)–(6), (8)–(10) теоремы 1 следует из теорем 2 и 3.

Доказательство (7) проводится по плану, принятому в [3].

Список литературы

Бесов О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы вложения. М.: Наука, 1996.
Трибель Х. Теория интерполяции. Функциональные пространства. Дифференциальные операторы. М.: Мир, 1980.
Берг Й., Лёфстрём Й. Интерполяционные пространства. М.: Мир, 1980.
Аджиев С.С. // Тр. МИАН. 1999. Т. 227. С. 7–42.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал