1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 495, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 13-16

ТОЧНЫЕ РЕШЕНИЯ СИСТЕМЫ НАВЬЕ–СТОКСА ДЛЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ В СЛУЧАЕ ЗАДАЧ, СВЯЗАННЫХ С НЕФТЕГАЗОВОЙ ОТРАСЛЬЮ

Академик РАН В. Б. Бетелин 1, *, В. А. Галкин 2, **, А. О. Дубовик 2, ***

1 Федеральный научный центр Научно-исследовательский институт системных исследований Российской академии наук
Москва, Россия

2 Сургутский филиал Федерального научного центра Научно-исследовательский институт системных исследований Российской академии наук
Москва, Россия

* E-mail: betelin@niisi.msk.ru
** E-mail: val-gal@yandex.ru
*** E-mail: alldubovik@gmail.com

Поступила в редакцию 15.09.2020
После доработки 15.09.2020
Принята к публикации 21.09.2020

Полный текст (PDF)

Аннотация

В рамках модели гидродинамики, описывающей течение вязкой несжимаемой жидкости, представлены классы точных решений, соответствующие вихревому и потенциальному течению. Исследование точных решений является необходимым условием для создания кернового симулятора, что связано с моделированием динамики жидкости в пористой среде и откликом месторождения на динамические воздействия с целью повышения нефтеотдачи.

Ключевые слова: гидродинамика, точные решения, переменная область, нефтегазовая отрасль

Рассматривается течение несжимаемой жидкости в открытой пространственной области {x} ∈ ∈ $D(t) \subset {{\mathbb{R}}_{n}}$ с границей $\partial D(t)$, где t – время. Условие несжимаемости жидкости предполагает неизменность объема D(t). Предполагается, что в указанной области жидкость имеет постоянную плотность ρ > 0, а ее динамика задается полем скоростей ${\mathbf{u}} = \{ {{u}_{i}}({\mathbf{x}},t)\} _{1}^{n}$ и давлением $p({\mathbf{x}},t)$, которые подчиняются уравнениям Навье–Стокса [1, 2] и закону сохранения массы в эйлеровых координатах:

(1)
$\begin{gathered} \frac{{\partial {{u}_{i}}}}{{\partial t}} + \sum\limits_j {{{u}_{j}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + {{\rho }^{{ - 1}}}\frac{{\partial p}}{{\partial {{x}_{i}}}} = {\text{div}}\left( {\varepsilon \,{\text{grad}}\,{{u}_{i}}} \right) + {{\rho }^{{ - 1}}}{{F}_{i}}} , \\ {\text{div}}\,{\mathbf{u}} = 0,\quad t > 0,\quad x \in D(t), \\ \end{gathered} $
где $\varepsilon = \eta {{\rho }^{{ - 1}}}$ – кинематическая вязкость жидкости, $\eta $ – динамическая вязкость, ${\mathbf{F}}({\mathbf{x}},t) = \{ {{F}_{i}}\} _{1}^{n}$ – плотность объемных сил. Ниже рассматривается случай, когда $\varepsilon = const$ ≥ 0, ${\mathbf{F}}({\mathbf{x}},t) \equiv 0$, ρ ≡ 1. Задачи управления течением жидкости особую актуальность приобретают в связи с необходимостью создания технологии “цифровое месторождение” [3–5]. Ниже рассмотрены точные решения системы (1) при дополнительных условиях, представляющих интерес для создания кернового симулятора. В частности, для нефтегазовой отрасли рассматриваемые ниже точные решения непосредственно связаны с моделированием динамики жидкости в пористой среде и откликом месторождения на динамические воздействия различных типов (механические, тепловые, электрические, химические и т.п.), что позволяет провести оптимизацию управляющих воздействий с целью повышения коэффициента извлечения нефти. Исследованию влияния тепловых эффектов на структуру течения посвящены работы [6–9], в том числе и таких вязких жидкостей, как нефть [8]. Представленный класс задач позволяет включить в рассмотрение модели деформации пластов в задачах гидрогеодинамики, описанные в [10].

Одним из важнейших вопросов построения кернового симулятора является получение точной динамики несжимаемой жидкости в пористой среде. Рассмотрим простейшую модель пористой среды, состоящую из дискретного набора точек – узлов сетки $\partial D(t) \subset {{\mathbb{R}}_{n}}$. В этом случае область течения $D(t) \equiv {{\mathbb{R}}_{n}}{\backslash }\partial D(t)$. На узлах сетки, являющихся границей области течения, потребуем выполнение условия прилипания

(2)
${\mathbf{u}}{{{\text{|}}}_{{\partial D(t)}}} = 0.$

Для построения точных решений системы (1) с условиями прилипания (2) воспользуемся нетривиальными точными решениями (V, Φ) задачи

(3)
$\left[ {{\mathbf{V}},{\text{rot}}\,{\mathbf{V}}} \right] = \nabla \Phi ,\quad {\text{div}}\,{\mathbf{V}} = 0,$
где отысканию подлежат гладкий потенциал Φ и векторное поле V на D(t).

ПРИМЕРЫ ТОЧНЫХ РЕШЕНИЙ ДЛЯ МОДЕЛЕЙ ПОРИСТОЙ СРЕДЫ

1. Рассмотрим модель пористой среды, состоящую из узлов плоской сетки ∂D(t) = $\pi \times {{\mathbb{Z}}_{2}} + 0.5$ × × (π, π) в пространстве ${{\mathbb{R}}_{2}}$. Случай сетки, состоящей из узлов, расположенных с шагом h, получается простой заменой пространственно-временных переменных в приведенных ниже формулах. Соответствующее точное решение задачи (1), (2) имеет следующий вид:

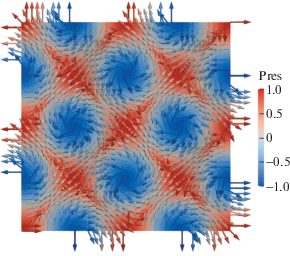
$\begin{gathered} {\mathbf{u}}({\mathbf{x}},t) = \exp ( - \varepsilon \lambda t)\left( {\begin{array}{*{20}{l}} {\sin (\sqrt \lambda {{x}_{2}})} \\ {\sin (\sqrt \lambda {{x}_{1}})} \end{array}} \right), \\ p({\mathbf{x}},t) = \exp ( - 2\varepsilon \lambda t)\cos (\sqrt \lambda {{x}_{2}})\cos (\sqrt \lambda {{x}_{1}}), \\ \lambda > 0. \\ \end{gathered} $

На рис. 1 изображено решение задачи в области ${{x}_{1}},\;{{x}_{2}} \in \left[ { - \pi ;\pi } \right]$ при λ = 4, в центре рисунка находится точка O(0; 0), t ≥ 0. Стрелки на рис. 1 соответствуют направлению поля скорости.

Рис. 1.

Структура течения.

Следует подчеркнуть, что течение структурировалось на квадраты, внутри которых вращаются вихри с центрами, расположенными в узлах сетки $\partial D(t) = \pi \times {{\mathbb{Z}}_{2}}$ + 0.5 × (π, π), в которых скорость течения обращается в нуль. На границах квадратов, расположенных под углами ±45° и центрами на сетке, жидкость скользит по касательной. Аналогичное структурирование течения проводящей жидкости наблюдалось при описании точного трехмерного решения системы уравнений магнитной гидродинамики с условием скольжения на границе параллелепипеда [11].

2. 3-D течение. Течение осуществляется между узлов сетки $\partial D(t) = \pi \times {{\mathbb{Z}}_{3}} + 0.25$ × (π, π, π) в пространстве ${{\mathbb{R}}_{3}}$. Соответствующее точное решение задачи (1), (2) в этой области имеет вид

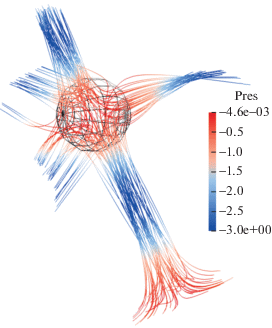
$\begin{gathered} u(x,t) = \left( \begin{gathered} \sin ({{x}_{2}}) - \cos ({{x}_{3}}) \hfill \\ \sin ({{x}_{3}}) - \cos ({{x}_{1}}) \hfill \\ \sin ({{x}_{1}}) - \cos ({{x}_{2}}) \hfill \\ \end{gathered} \right)\exp ( - \varepsilon t), \\ p(x,t) = - \frac{1}{2}(u,u). \\ \end{gathered} $

Рисунок 2 иллюстрирует линии тока в точке прилипания, где поле давления равно нулю.

Рис. 2.

Линии тока, проходящие через сферу радиуса 1 с центром в точке ${{x}_{1}} = {{x}_{2}} = {{x}_{3}} = \frac{\pi }{4}$.

Приведенные выше примеры точных решений описывают чисто вихревые течения.

3. Примеры потенциальных течений в плоской области с переменной геометрией. В случае потенциального течения жидкости ${\mathbf{u}} = \nabla \Psi $, u – вектор скорости жидкости, решение уравнений гидродинамики с условием скольжения на границе сводится к решению задачи Неймана для уравнения Лапласа на нахождение потенциала скорости Ψ(t, x(t)):

$\Delta \Psi = 0,\quad {{\left. {\frac{{\partial \Psi }}{{\partial n}}} \right|}_{{\partial D(t)}}} = {{\left. {{\mathbf{V}}\left( {{{x}_{1}},{{x}_{2}},t} \right) \cdot {\mathbf{n}}} \right|}_{{\partial D(t)}}}{\text{,}}$
$p = - \frac{1}{2}{{\left( {\nabla \Psi } \right)}^{2}} - \frac{{d\Psi }}{{dt}},\quad ({{x}_{1}},{{x}_{2}}) \in D(t) \subset {{\mathbb{R}}_{2}}.$

Закон деформации области D(t) задан следующей динамикой:

$\frac{{d{\mathbf{x}}}}{{dt}} = {\mathbf{V}}\left( {{\mathbf{x}},t} \right),\quad {\mathbf{x}} = ({{x}_{1}},{{x}_{2}}),$
где x(t) – положение точки в области D(t), при условии, что в момент времени t = 0 она находилась в точке $(x_{1}^{{(0)}},x_{2}^{{(0)}}) \in D\left( 0 \right)$.

Далее описывается решение двух тестовых задач. Численное решение получено методом контрольного объема. Результаты расчетов совпали в пределах точности разностной схемы с точными решениями задач.

3.1. Первый тестовый расчет проведен в случае, когда деформация области происходит под действием преобразований, заданных векторным полем V = {α(t)x; –α(t)y}, где α(t) – заданная функция времени. (Ниже в тестовых расчетах α(t) = cosπt, D(0) – квадрат со стороной 1.) При таком преобразовании области ее объем сохраняется, что соответствует деформации области, заполненной несжимаемой жидкостью. В этом случае область D(t) с течением времени трансформируется из квадрата в прямоугольник, вытянутый вдоль оси Ox1, а затем возвращается в исходное состояние. Далее область трансформируется в прямоугольник, вытянутый вдоль координатной оси Ox2, возвращается в исходное положение и т.д.

Аналитическое решение задачи имеет вид

$\begin{gathered} \Psi = \frac{{\alpha \left( t \right)}}{2}(x_{1}^{2} - x_{2}^{2}), \\ p = - \frac{3}{2}\alpha \left( t \right)(x_{1}^{2} + x_{2}^{2}) - \frac{{\alpha {\kern 1pt} '\left( t \right)}}{2}(x_{1}^{2} - x_{2}^{2}). \\ \end{gathered} $

Далее проиллюстрированы результаты расчетов в моменты времени при t = 0.2 (рис. 3). На рисунках цветом отображены значения поля давления p, линиями и стрелками показано направление поля скорости ${\mathbf{u}} = \nabla \Psi $, соответствующее потенциальному течению жидкости.

Рис. 3.

Линия тока и поле давления в прямоугольнике D(t) при t = 0.2.

3.2. В следующем тестовом расчете D(0) – круг радиуса 1 с выколотым центром, который превращается в кольцо D(t), а затем возвращается в исходное состояние. Внешний радиус кольца в момент времени t > 0 положим равным $\sqrt {1 + {{\alpha }^{2}}\left( t \right)} $, а внутренний – α(t), где $\alpha (t) = {\text{sin}}~\pi t \geqslant 0$.

Трансформация границы области задана векторным полем в полярных координатах:

${\mathbf{V}}\left( {\rho ,\varphi ,t} \right) = \left\{ {\frac{{\alpha \left( t \right)\alpha {\kern 1pt} '\left( t \right)}}{\rho };\,\,0} \right\}.$

При таком преобразовании области ее объем сохраняется. Точное решение имеет вид

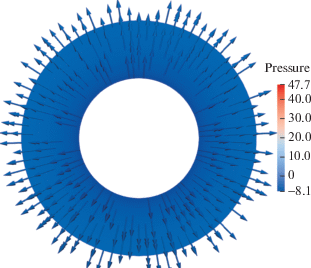
$\begin{gathered} \Psi = \alpha \left( t \right)\alpha {\kern 1pt} '\left( t \right)\ln \rho , \\ p = - \frac{3}{2}\frac{{{{\alpha }^{2}}\left( t \right){{{\alpha '}}^{2}}\left( t \right)}}{{{{\rho }^{2}}}} - {{\pi }^{2}}\cos \left( {2\pi t} \right)\ln \rho . \\ \end{gathered} $

Ниже приведены результаты расчетов в моменты времени t = 0.2 (рис. 4). На рисунках цветом отображены значения поля давления p, стрелками показано направление поля скорости ${\mathbf{u}} = \nabla \Psi $, соответствующее потенциальному течению жидкости. В начальный момент времени и при t = 1 жидкость покоится.

Рис. 4.

Поле скорости и поле давления в D(t) при t = 0.2.

Список литературы

  1. Ландау Л.Д. Лифшиц Е.М. Теоретическая физика: Уч. пособ.: Для вузов. В 10 т. Т. VI. Гидродинамика. 5-е изд., стереотип. М.: Физматлит, 2001. 736 с.

  2. Монин А.С., Яглом А.М. Статистическая гидромеханика. Механика турбулентности. Ч. 1. М.: Наука, 1986. 640 с.

  3. Бетелин В.Б., Галкин В.А. Управление параметрами несжимаемой жидкости при изменении во времени геометрии течения // ДАН. 2015. Т. 463. № 2. С. 149–151.

  4. Галкин В.А., Дубовик А.О., Епифанов А.А. Приближенные методы для уравнений несжимаемой жидкости // ЖВМиМФ. 2017. Т. 57. № 2. С. 275–284.

  5. Вольпин С.Г., Юдин В.А., Кац Р.М., Афанаскин И.В., Галкин В.А. Применение суперкомпьютерных технологий – ключ к решению проблем повышения нефтеотдачи на месторождениях России // В сб.: СПб науч. форум. VIII встреча лауреатов нобелевской премии. СПб. 2013. С. 90–92.

  6. Галич Н.Е. Тепловая неустойчивость и пробой движущихся вязких жидкостей в электрическом поле и при поглощении света // ЖТФ. 1989. Т. 59. Вып. 7. С. 10–17.

  7. Алтоиз Б.А., Савин Н.В., Шатагина Е.А. Влияние тепловыделения в микропрослойке жидкости при измерении ее вязкости // ЖТФ. 2014. Т. 84. В. 5. С. 21–27.

  8. Куштанова Г.Г. Физика геосферы. Казань: Изд-во КазГУ, 2004. 44 с.

  9. Семенов Н.Н. Цепные реакции. М.: Госхимтехиздат, 1934.

  10. Шестаков В.М. Гидрогеодинамика. М.: Изд-во МГУ, 1995. 368 с.

  11. Бетелин В.Б., Галкин В.А., Гореликов А.В. Алгоритм типа предиктор–корректор для численного решения уравнения индукции в задачах магнитной гидродинамики вязкой несжимаемой жидкости // ДАН. 2015. Т. 464. № 5. С. 525–528.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал