1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 495, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 26-30

О СУЩЕСТВОВАНИИ ФОКУСНЫХ ОСОБЕННОСТЕЙ В ОДНОЙ МОДЕЛИ ВОЛЧКА ЛАГРАНЖА С ВИБРИРУЮЩЕЙ ТОЧКОЙ ПОДВЕСА

А. В. Борисов 1, 2, 3, *, П. Е. Рябов 1, 2, 4, **, С. В. Соколов 1, 2, ***

1 Институт машиноведения им. А.А. Благонравова Российской академии наук
Москва, Россия

2 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

3 Математический институт им. В.А. Стеклова Российской академии наук
Москва, Россия

4 Финансовый университет при Правительстве Российской Федерации
Москва, Россия

* E-mail: borisov@rcd.ru
** E-mail: PERyabov@fa.ru
*** E-mail: sokolov.sv@phystech.edu

Поступила в редакцию 10.09.2020
После доработки 30.10.2020
Принята к публикации 01.11.2020

Полный текст (PDF)

Аннотация

Рассматривается вполне интегрируемая гамильтонова система с двумя степенями свободы, которая описывает динамику волчка Лагранжа с вибрирующей точкой подвеса. Наглядно представлены результаты исследования проблемы устойчивости положений равновесия. Как оказалось, оба положения равновесия при наличии вибрирующей точки подвеса могут быть неустойчивыми, что соответствует существованию фокусных особенностей в указанной модели.

Ключевые слова: вполне интегрируемые гамильтоновы системы, волчок Лагранжа, фокусная особенность

Настоящее сообщение посвящено топологическому анализу положений равновесия динамически симметричного твердого тела в однородном поле силы тяжести. Как известно [1, 2], нахождение точек ранга ноль, исследование их невырожденности и типа является первым этапом анализа фазовой топологии любой вполне интегрируемой гамильтоновой системы. Одна из точек тела, лежащая на оси симметрии (точка подвеса), совершает высокочастотные периодические или условно-периодические  колебания (вибрации) малой амплитуды. Из-за наличия вибраций точки подвеса дифференциальные уравнения движения твердого тела, описывающие его ориентацию относительно системы координат, явно зависят от времени. В работах А.П. Маркеева [3, 4] указано преобразование, приводящее исходные уравнения движения, записанные в форме уравнений Эйлера–Пуассона, к приближенной системе относительно новых переменных, которая также имеет форму уравнений Эйлера–Пуассона, но не зависит явно от времени. Оказывается, что полученная система дифференциальных уравнений является вполне интегрируемой по Лиувиллю гамильтоновой системой с двумя степенями свободы. В данной работе мы подвергаем полученную систему топологическому анализу и наглядно демонстрируем проблемы исследования устойчивости положений равновесия на основе определения типа особенностей [5].

Для динамически симметричного твердого тела, когда центр тяжести лежит на оси динамической симметрии, соответствующая система дифференциальных уравнений имеет вид обобщенных уравнений Кирхгофа

(1)
${\mathbf{\dot {M}}} = {\mathbf{M}} \times \frac{{\partial H}}{{\partial {\mathbf{M}}}} + \gamma \times \frac{{\partial H}}{{\partial \gamma }},\quad \dot {\gamma } = \gamma \times \frac{{\partial H}}{{\partial {\mathbf{M}}}}$
с функцией Гамильтона

(2)
$H = \frac{1}{2}(M_{1}^{2} + M_{2}^{2} + cM_{3}^{2}) + a{{\gamma }_{3}} - \frac{1}{2}b\gamma _{3}^{2}.$

Здесь через ${\mathbf{M}} = \{ {{M}_{1}},{{M}_{2}},{{M}_{3}}\} $ и $\gamma = \{ {{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}}\} $ обозначены вектор кинетического момента и единичный орт вертикали в системе главных осей, жестко связанных с твердым телом и проходящих через точку закрепления. Параметры a, b и c, cогласно [3, 6], имеют явный физический смысл. Параметр a связан с расположением центра масс вдоль вертикальной оси и в дальнейшем для конкретного исследования знак параметра a предполается фиксированным. Параметр b характеризует разность усреднений квадратов проекций компонент вектора скорости точки подвеса на оси OX и OZ в системе координат $OXYZ$ с началом в точке подвеса, который может принимать как положительные, так и отрицательные значения. Положительный параметр c характеризует отношение главных компонент тензора инерции динамически симметричного твердого тела.

Уравнения (1) могут быть представлены в гамильтоновом форме

${\mathbf{\dot {M}}} = \{ {\mathbf{M}},H\} ,\quad \dot {\gamma } = \{ \gamma ,H\} $
со скобкой Ли–Пуассона, соответствующей алгебре Ли $e(3)$,

(3)
$\begin{gathered} \{ {{M}_{i}},{{M}_{j}}\} = - {{\varepsilon }_{{ijk}}}{{M}_{k}},\quad \{ {{M}_{i}},{{\gamma }_{j}}\} = - {{\varepsilon }_{{ijk}}}{{\gamma }_{k}}, \\ \{ {{\gamma }_{i}},{{\gamma }_{j}}\} = 0. \\ \end{gathered} $

Скобка Ли–Пуассона (3) является вырожденной, она обладает двумя функциями Казимира, коммутирующими относительно структуры (3) с любой функцией от ${\mathbf{M}},{\mathbf{\gamma }}$:

$\begin{array}{*{20}{c}} {L = ({\mathbf{M}},{\mathbf{\gamma }})\quad ({\text{интеграл}}\;{\text{площадей}}),} \\ {\Gamma = {\text{|}}{\mathbf{\gamma }}{{{\text{|}}}^{2}}\quad ({\text{геометрический}}\;{\text{интеграл}}).} \end{array}$

Фазовое пространство $\mathcal{P}$ задается в виде касательного расслоения $T{{\mathbb{S}}^{2}}$ к двумерной сфере ${{\mathbb{S}}^{2}}$

$\mathcal{P} = \{ ({\mathbf{M}},{\mathbf{\gamma }}){\kern 1pt} :\;L = \ell ,\,\,\Gamma = 1\} .$

Система (1) допускает один дополнительный первый интеграл движения – интеграл Лагранжа

$F = {{M}_{3}}.$

Функция F вместе с гамильтонианом H образуют на $\mathcal{P}$ полный инволютивный набор интегралов системы (1). Согласно теореме Лиувилля–Арнольда, регулярная поверхность уровня первых интегралов вполне интегрируемой гамильтоновой системы представляет собой несвязное объединение торов, заполненных условно-периодическими траекториями. Определим интегральное отображение 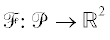, полагая (f, h) = $\mathcal{F}({\mathbf{x}})$ = = (F(x), H(x)). Отображение $\mathcal{F}$ принято также называть отображением момента. Обозначим через $\mathfrak{C}$ совокупность всех критических точек отображений момента, т.е. точек, в которых ${\text{rank}}\,d\mathcal{F}(x)$ < 2. Множество критических значений $\Sigma = \mathcal{F}(\mathfrak{C} \cap \mathcal{P})$ называется бифуркационной диаграммой. Цель настоящей публикации состоит в определении и исследовании типа особенностей ранга ноль отображения момента, которым соответствуют положения равновесия.

1. НЕОБХОДИМЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

В этом разделе мы приводим результаты, касающиеся аналитической классификации типов критических точек ранга ноль. Напомним некоторые факты и определения, связанные с понятием типа критической точки в интегрируемой системе [1].

Пусть $\mathcal{P}$ – симплектическое многообразие. Любой гладкой функции $F{\kern 1pt} :\;\mathcal{P} \to \mathbb{R}$ сопоставляется гамильтоново векторное поле на $\mathcal{P}$, обозначаемое ${\text{sgrad}}F$. Скобки Пуассона, порожденные симплектической структурой, обозначаем через $\{ \cdot , \cdot \} $, так что дифференциальные уравнения системы ${\text{sgrad}}F$ имеют вид

$\dot {x} = \{ F,x\} .$

Пусть $dim\mathcal{P} = 2n$ и гамильтонова система ${\text{sgrad}}H$ имеет n функционально независимых первых интегралов

${{F}_{1}}, \ldots ,{{F}_{n}}$
в инволюции ($\{ {{F}_{i}},{{F}_{j}}\} = 0$). Точка $\xi \in \mathcal{P}$ называется критической ранга $k < n$, если ранг системы векторов ${\text{sgrad}}{{F}_{i}}$ в точке $\xi $ равен k. Введем понятие типа критической точки, следуя [1].

Рассмотрим критическую точку $\xi $ ранга $n - m$ ($m > 0$). Пусть далее в этом разделе индекс i пробегает множество 1, …, m. Линейной заменой c постоянными коэффициентами системы функций ${{F}_{1}}, \ldots ,{{F}_{n}}$ можно добиться того, чтобы точка ξ была критической для каждой из функций Fi и регулярной для всех остальных. Тогда ${\text{sgrad}}{{F}_{i}}(\xi ) = 0$ и линеаризация этого поля в точке ξ есть симплектический оператор ${{\mathfrak{a}}_{i}}{\kern 1pt} :\;{{T}_{\xi }}M \to {{T}_{\xi }}M$. Линейная оболочка $\mathfrak{A}(\xi )$ таких операторов есть подалгебра в алгебре всех симплектических операторов на ${{T}_{\xi }}M$.

Определение 1 [1]. Точка ξ называется невырожденной критической точкой ранга $n - m$, если $\mathfrak{A}(\xi )$ есть подалгебра Картана, что равносильно следующим требованиям:

1) симплектические операторы ${{\mathfrak{a}}_{i}}$ линейно независимы $(dim\mathfrak{A}(\xi ) = m)$;

2) существует оператор $\mathfrak{a} \in \mathfrak{A}(\xi )$, у которого все собственные числа различны.

Напомним, что собственные числа симплектического оператора разбиваются на группы: пары чисто мнимых $ \pm {\text{i}}\beta $, пары вещественных ±α и четверки комплексных $ \pm \alpha \pm {\text{i}}\beta $ ($\alpha \beta \ne 0$). Для оператора ${{\mathfrak{a}}_{i}}$ в проекции на корневые подпространства таких групп поле ${\text{sgrad}}{{F}_{i}}$ имеет соответственно центр, седло или фокус. Оператор $\mathfrak{a} \in \mathfrak{A}(\xi )$ с различными собственными числами называется регулярным элементом. Выбрав в невырожденной точке регулярный элемент, обозначим через ${{m}_{1}},\;{{m}_{2}},\;{{m}_{3}}$ соответственно количество центров, седел и фокусов $(m = {{m}_{1}} + {{m}_{2}} + 2{{m}_{3}})$. От выбора регулярного элемента эти целые неотрицательные числа не зависят.

Определение 2 [1]. Четверка $(n - m,{{m}_{1}}$, m2, m3) называется  типом невырожденной критической точки ξ.

Для систем с двумя степенями свободы часто используются следующие наглядные обозначения и названия. Точки ранга ноль типа (0, 2, 0, 0) называются точками типа центр-центр, типа (0, 1, 1, 0) – центр-седло, типа (0, 0, 2, 0) – седло-седло, наконец, точки типа (0, 0, 0, 2) называются точками типа фокус-фокус.

2. ПОЛОЖЕНИЯ РАВНОВЕСИЯ – КРИТИЧЕСКИЕ ТОЧКИ РАНГА НОЛЬ ОТОБРАЖЕНИЯ МОМЕНТА

Для гамильтониана (2) существуют два положения равновесия (критические точки ранга 0 отображения момента $\mathcal{F}$), которые имеют в $\mathcal{P}$ следующие координаты:

${{\xi }^{ \pm }}{\kern 1pt} :\;{{M}_{1}} = {{M}_{2}} = {{\gamma }_{1}} = {{\gamma }_{2}} = 0,\quad {{M}_{3}} = \pm \ell ,\quad {{\gamma }_{3}} = \pm 1.$

Положениям равновесия отвечают стационарные вращения твердого тела вокруг оси симметрии с постоянной угловой скоростью. Соответствующие значения постоянных первых интегралов определяют две точки P± на плоскости ${{\mathbb{R}}^{2}}(f,h)$:

${{P}^{ + }}{\kern 1pt} :\;\left\{ {\begin{array}{*{20}{l}} {f = \ell } \\ {h = \frac{1}{2}c{{\ell }^{2}} + a - \frac{b}{2},} \end{array}} \right.\quad {{P}^{ - }}{\kern 1pt} :\;\left\{ {\begin{array}{*{20}{l}} {f = - \ell ,} \\ {h = \frac{1}{2}c{{\ell }^{2}} - a - \frac{b}{2}.} \end{array}} \right.$

Следующая теорема дает ответ, когда обе точки P± будут изолированными точками бифуркационной диаграммы.

Теорема 1. Изолированным точкам P±бифуркационной диаграммы для случая Лагранжа с вибрирующей точкой подвеса в тех случаях, когда они имеются, т.е. при

$\begin{gathered} {{\ell }^{2}} < 4(a - b)\quad (для\;{{P}^{ + }}) \\ и\quad {{\ell }^{2}} < - 4(a + b)\quad (для\;{{P}^{ - }}) \\ \end{gathered} $
отвечают особенности типа фокус-фокус (0, 0, 0, 2) в $\mathcal{P}$.

Доказательство. Рассмотрим систему (1) с гамильтонианом (2) в явном виде

$\begin{gathered} {{{\dot {M}}}_{1}} = (c - 1){{M}_{2}}{{M}_{3}} + (a - b{{\gamma }_{3}}){{\gamma }_{2}}, \\ {{{\dot {\gamma }}}_{1}} = c{{\gamma }_{2}}{{M}_{3}} - {{\gamma }_{3}}{{M}_{2}}, \\ \end{gathered} $
(4)
$\begin{gathered} {{{\dot {M}}}_{2}} = - (c - 1){{M}_{1}}{{M}_{3}} - (a - b{{\gamma }_{3}}){{\gamma }_{1}}, \\ {{{\dot {\gamma }}}_{2}} = - c{{\gamma }_{1}}{{M}_{3}} + {{\gamma }_{3}}{{M}_{1}}, \\ {{{\dot {M}}}_{3}} = 0,\quad {{{\dot {\gamma }}}_{3}} = {{\gamma }_{1}}{{M}_{2}} - {{\gamma }_{2}}{{M}_{1}}. \\ \end{gathered} $

Для этой системы точки ${{\xi }^{ \pm }}$ являются положениями равновесия. Рассмотрим линеаризацию системы (4) в точках ${{\xi }^{ \pm }}$. Выберем в окрестности указанных точек в $\mathcal{P}$ локальные координаты ${{M}_{1}},{{M}_{2}}$, γ1, γ2 и линеаризуем систему (4) в окрестности этих точек. Получим следующие системы (верхний знак соответствует линеаризации в окрестности точки ${{\xi }^{ + }}$, а нижний знак – в окрестности точки ${{\xi }^{ - }}$):

(5)
$\begin{gathered} {{{\dot {M}}}_{1}} = \pm \ell (c - 1){{M}_{2}} + (a \mp b){{\gamma }_{2}}, \\ {{{\dot {M}}}_{2}} = \mp \ell (c - 1){{M}_{1}} - (a \mp b){{\gamma }_{1}}, \\ {{{\dot {\gamma }}}_{1}} = \mp {{M}_{2}} \pm c\ell {{\gamma }_{2}},\quad {{{\dot {\gamma }}}_{2}} = \pm {{M}_{1}} \mp c\ell {{\gamma }_{1}}. \\ \end{gathered} $

Тогда матрицы $\mathcal{A}({{\xi }^{ \pm }})$ систем (5) имеют вид матриц размера 4 × 4:

$\mathcal{A}({{\xi }^{ \pm }}) = \left( {\begin{array}{*{20}{c}} 0&{ \pm (c - 1)\ell }&0&{a \mp b} \\ { \mp (c - 1)\ell }&0&{ - (a \mp b)}&0 \\ 0&{ \mp 1}&0&{ \pm c\ell } \\ { \pm 1}&0&{ \mp c\ell }&0 \end{array}} \right).$

Характеристические уравнения для матриц $\mathcal{A}({{\xi }^{ \pm }})$ запишутся в виде

(6)
${{f}_{1}}(\mu ) \cdot {{f}_{2}}(\mu ) = 0,$
где

$\begin{array}{*{20}{c}} {{{f}_{1}}(\mu ) = {{\mu }^{2}} \pm {\text{i}}(2c - 1)\ell \mu - c(c - 1){{\ell }^{2}} \mp (a \mp b),} \\ {{{f}_{2}}(\mu ) = {{\mu }^{2}} \mp {\text{i}}(2c - 1)\ell \mu - c(c - 1){{\ell }^{2}} \mp (a \mp b).} \end{array}$

Cобственные значения матриц $\mathcal{A}({{\xi }^{ \pm }})$, которые являются корнями характеристического уравнения (6), имеют вид

$\alpha + {\text{i}}\beta ,\quad - \alpha + {\text{i}}\beta ,\quad \alpha - {\text{i}}\beta ,\quad - \alpha - {\text{i}}\beta ,$
где

$\alpha = \frac{{\sqrt { \pm 4(a \mp b) - {{\ell }^{2}}} }}{2},\quad \beta = \pm \frac{1}{2}(1 - 2c)\ell .$

При условии, сформулированном в теореме для точек бифуркационной диаграммы P±, т.е. при ${{\ell }^{2}} < 4(a - b)$ и ${{\ell }^{2}} < - 4(a + b)$, числа α и β вещественные. Более того, когда α и β отличны от нуля, то все четыре собственных значения действительно различны, а следовательно, особенности ${{\xi }^{ \pm }}$ невырождены и имеют тип фокус-фокус (0, 0, 0, 2) в $\mathcal{P}$.

Замечание 1. Конечно, при некоторых значениях $\ell $ и c собственные значения могут быть кратными. Так, например, происходит при $\ell $ = 0, $\ell = \pm 2\sqrt { \pm (a \mp b)} $ или при $c = \frac{1}{2}$. При $\ell = \pm 2\sqrt {a - b} $ изолированная точка P+ на бифуркационной диаграмме оказывается на границе образа отображения момента. В момент попадания на эту границу точка становится вырожденной, а затем, по мере роста $\ell $, т.е. когда ${\text{|}}\ell {\text{|}}$ становится больше, чем $2\sqrt {a - b} $, точка P+ меняет тип с фокус-фокус на центр-центр, т.е. “верхнее положение” ${{\xi }^{ + }}$ становится устойчивым положением равновесия. Такой вывод согласуется с результатом, полученным ранее другим классическим методом в работе Маркеева [6]. Рассмотрим “нижнее положение” равновесия ${{\xi }^{ - }}$, которому соответствует на бифуркационной диаграмме точка P–. При значениях параметра интеграла площадей ${\text{|}}\ell {\text{|}}$ больше, чем $2\sqrt { - (a + b)} $, положение равновесия устойчиво, что соответствует особенности типа центр-центр. В момент, когда $\ell = \pm \sqrt { - (a + b)} $, точка P– все еще остается устойчивым положением равновесия, но особенность уже вырожденная, а вот при уменьшении интеграла площадей, т.е. когда ${\text{|}}\ell {\text{|}} < \sqrt { - 2(a + b)} $, точка P– становится изолированной особенностью, меняя тип с центр-центр на фокус-фокус, что ведет к тому, что “нижнее положение” ${{\xi }^{ - }}$ становится неустойчивым положением равновесия.

При $\ell = 0$ или при $c = \frac{1}{2}$ тип особенности сохраняется. Для этого необходимо заменить гамильтониан H на новый гамильтониан $\tilde {H}$ в виде линейной комбинации $\tilde {H} = H + \lambda F$, для которого по-прежнему имеем в точках ${{\xi }^{ \pm }}$ особенность ранга 0. Для такого нового гамильтониана $\tilde {H}$ все собственные значения характеристического уравнения линеаризованной системы станут вновь различными, и мы возвращаемся в предыдущую ситуацию общего положения.

Замечание 2. Отметим также случай, когда изолированные точки P+ и P– на бифуркационной диаграмме могут совпадать. Это происходит при нулевом значении интеграла площадей $\ell $ и a = 0; $b < 0$, т.е. когда центр масс помещен в начало системы координат, связанным с твердым телом, но при этом параметр b, который отвечает за воздействие на точку подвеса вибрирующего потенциала, должен быть отрицателен. Это ведет к существованию почти торической интегрируемой системы с двойным pinched тором в прообразе изолированного критического значения P+ = = P– = $P\left( {0; - \tfrac{b}{2}} \right)$ отображения момента [7].

ЗАКЛЮЧЕНИЕ

В работе рассмотрены положения равновесия динамически симметричного твердого тела с вибрирующей точкой подвеса, но в отличие от классического подхода, использованного в [6] при исследовании устойчивости “верхнего положения” равновесия, анализ типа особенностей отображения момента позволил установить соотношения, при которых “нижнее положение” равновесия теряет устойчивость. Уникальным также является появление двойного pinched тора в рассматриваемой механической системе.

Список литературы

  1. Болсинов А.В., Фоменко А.Т. Интегрируемые гамильтоновы системы. Геометрия, топология, классификация. Т. 1, 2. Ижевск: Изд. дом ”Удмуртский университет“, 1999. 444 с., 447 с.

  2. Ryabov P.E., Oshemkov A.A., Sokolov S.V. The Integrable Case of Adler – van Moerbeke. Discriminant Set and Bifurcation Diagram // Regul. Chaotic Dyn. 2016. V. 21. № 5. P. 581–592.

  3. Маркеев А.П. К теории движения твердого тела с вибрирующим подвесом // ДАН. 2009. Т. 427. № 6. С. 771–775.

  4. Маркеев А.П. Об уравнениях приближенной теории движения твердого тела с вибрирующей точкой подвеса // ПММ. 2011. Т. 75. № 2. С. 193–203.

  5. Bolsinov A.V., Borisov A.V., Mamaev I.S. Topology and Stability of Integrable Systems // Russian Math. Surveys. 2010. V. 65. № 2. P. 259–318.

  6. Маркеев А.П. O движении тяжелого динамически симметричного твердого тела с вибрирующей точкой подвеса // Известия РАН. МТТ. 2012. Т. 47. № 4. С. 3–10.

  7. San Vu Ngoc. On semi-global invariants for focus–focus singularities // Topology. 2003. V. 42. № 2. P. 365–380.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал