1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 495, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 44-47

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ИСКУССТВЕННЫХ ЛЕДОВЫХ ОСТРОВОВ МЕТОДАМИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Член-корреспондент РАН И. Б. Петров 1, М. В. Муратов 1, *, Ф. И. Сергеев 1

1 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

* E-mail: max.muratov@gmail.com

Поступила в редакцию 10.07.2020
После доработки 16.07.2020
Принята к публикации 15.09.2020

Полный текст (PDF)

Аннотация

Работа посвящена численному моделированию упругих воздействий на искусственные ледовые острова, возникающих в результате ударных воздействий при бурении, а также из-за давления конструкций, расположенных на острове. Для численного решения этой задачи был использован сеточно-характеристический метод с интерполяцией на регулярных и неструктурированных сетках. Сеточно-характеристический метод наиболее точно описывает динамические процессы в задачах сейсморазведки, поскольку учитывает природу волновых явлений. Численный метод позволяет строить корректные вычислительные алгоритмы на границах и контактных границах области интегрирования. В работе исследуется процесс распространения упругих волн в рассматриваемой геологической среде, моделируется распределение напряжений, а также исследуется устойчивость ледяного острова к разрушению с применением критерия Мизеса.

Ключевые слова: математическое моделирование, сеточно-характеристический метод, ледовый остров, воздействие бура, воздействие статической нагрузки

Искусственные ледовые острова представляют собой дешевую и экологически чистую альтернативу обычным буровым платформам для добычи нефти и газа в условиях Арктики. Подход уже успешно реализован в Канаде [1]. Как отмечено в [2], актуальной проблемой безопасности конструкций и персонала на поверхности ледового острова является возможность его разрушение в результате бурения и превышенной статической нагрузки, расположенных на нем сооружений.

В современном программном обеспечении для изучения устойчивости таких структур обычно используется метод конечных элементов [3, 4]. Для моделирования распространения сейсмических волн исследователи обычно используют конечно-разностные методы [5], метод спектральных элементов [6], разрывный метод Галеркина [7, 8] и сеточно-характеристический метод [9]. В данной работе используется сеточно-характеристический метод с интерполяцией на регулярных прямоугольных и параллелепипедных сетках и неструктурированные треугольных и тетраэдральных сетках. Такой подход уже показал хорошую применимость при решении задач сейсморазведки в трещиноватых средах [10].

ПОСТАНОВКА ЗАДАЧИ

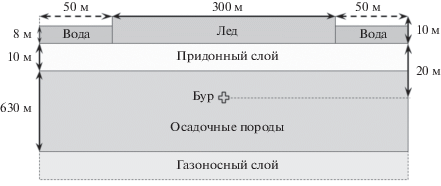
Область моделирования распространения волн представляет собой ледовый остров, окруженный морской водой и опирающийся на твердую почву. Геометрические размеры области приведены на рис. 1. Лед, вода и почва считаются однородными. Упругие характеристики (продольная и поперечная скорость распространения звука и плотность среды) приведены в табл. 1.

Рис. 1.

Схема расчетной области.

Таблица 1.

Значения упругих характеристик

Среда Скорость P-волны, м/с Скорость S-волны, м/с Плотность, кг/м3
Лед 3940 2493 917
Вода 1500 – 1025
Придонный слой 1806 316 2000
Осадочная порода 2250 1000 2000

На ледяном острове моделируются следующие виды нагрузок:

1) ударная нагрузка воздействия бура;

2) воздействие статической нагрузки сооружения.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Определяющая система уравнений линейно-упругой среды может быть представлена в виде

$\begin{gathered} \rho \frac{{\partial {{V}_{i}}}}{{\partial t}} = \frac{{\partial {{T}_{{ji}}}}}{{\partial {{x}_{j}}}},~ \\ ~\frac{{\partial {{T}_{{ij}}}}}{{\partial t}} = \lambda \left( {\mathop \sum \limits_k \frac{{\partial {{V}_{k}}}}{{\partial {{x}_{k}}}}} \right){{I}_{{ij}}} + \mu \left( {\frac{{\partial {{V}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{V}_{j}}}}{{\partial {{x}_{i}}}}} \right), \\ \end{gathered} $
где Vi – компонента скорости, Tij – тензора напряжений, ρ – плотность среды, λ и μ – коэффициенты Ламе, Iij – компонента единичного тензора. Введя вектор переменных ${\mathbf{u}} = \{ {{V}_{x}},{{V}_{y}},{{V}_{z}},{{T}_{{xx}}}$, Tyy, Tzz,, Txy, Txz,Tyz}, систему приводим к виду

$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \mathop \sum \limits_{i = 1,2,3} {{A}_{i}}\frac{{\partial {\mathbf{u}}}}{{\partial {{\xi }_{i}}}} = 0.$

ЧИСЛЕННЫЙ МЕТОД

Численное решение находится с применение сеточно-характеристического метода [9, 10]. Осуществляя покоординатное расщепление, заменой переменных система сводится к системе независимых скалярных уравнений переноса в инвариантах Римана:

$\frac{{\partial {\mathbf{w}}}}{{\partial t}} + {{{\Omega }}_{i}}\frac{{\partial {\mathbf{w}}}}{{\partial \xi _{i}^{'}}} = 0,\quad i = 1,2,3.$

Из временного слоя n соответствующая компонента вектора w переносится на временной слой n + 1 по формуле

$w_{k}^{{n + 1}}(\xi _{i}^{'}) = w_{k}^{n}(\xi _{i}^{'} - {{\omega }_{k}}\tau ),$
где τ – шаг по времени.

После того как все значения перенесены, происходит обратный переход к вектору искомых значений u.

Значения в каждой точке находятся с использованием значений в опорных точках сетки ${\mathbf{u}}\left( {{{{\mathbf{r}}}_{{ijkl}}}} \right)$ и весов этих точек ${{p}_{{ijkl}}}\left( {\mathbf{r}} \right)$ по формуле

${\mathbf{u}}\left( {\mathbf{r}} \right) = \mathop \sum \limits_{i,j,k,l} {{p}_{{ijkl}}}\left( {\mathbf{r}} \right){\mathbf{u}}\left( {{{{\mathbf{r}}}_{{ijkl}}}} \right).$

УСЛОВИЯ НА ГРАНИЦАХ И КОНТАКТНЫХ ГРАНИЦАХ

Граничное условие в общем виде записывается как

${\mathbf{Du}}\left( {{{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}},t + \tau } \right) = {\mathbf{d}},$
где D – некоторая матрица размера 9 × 3 для трехмерного случая (5 × 2 – для двумерного), d – вектор, ${\mathbf{u}}\left( {{{\xi }_{1}},{{\xi }_{2}},t + \tau } \right)$ – значение искомых значений скорости и компонент тензора напряжений в граничной точке на следующем временном шаге.

На границах области интегрирования использовались граничные условия:

1. На боковых границах использовалось поглощающее граничное условие:

${v}_{{k - 2}}^{n} = {v}_{{k - 1}}^{n} = {v}_{k}^{n},\quad T_{{k - 2}}^{n} = T_{{k - 1}}^{n} = T_{k}^{n},$
где индекс k соответствует граничному узлу сетки, k – 1 и k – 2 – его соседи по одной оси.

2. На границах среды с воздухом задавалось условие свободной границы:

${\mathbf{Tn}} = 0.$

3. Граничное условие постоянного давления задавалось на контакте здания и ледяного острова. Оно записывается следующим образом:

$p = {{T}_{{yy}}} = {{P}_{0}},\quad {{T}_{{xx}}} = {{T}_{{xy}}} = 0,$
где P0 – постоянное давление, оказываемое зданием на поверхность земли.

На контактных границах между слоями использовались следующие условия:

1. Условие полного слипания задавалось между слоями твердых сред:

${{{\mathbf{v}}}_{a}} = {{{\mathbf{v}}}_{b}},\quad {{{\mathbf{f}}}_{a}} = - {{{\mathbf{f}}}_{b}},$
где v – векторы скорости в контактных точках, f – силы, действующие на контактные границы, a и b – точки на первом и втором контактирующих слоях.

2. Условие свободного скольжения задавалось между ледовым островом и землей. Его можно записать в виде

${{{\mathbf{v}}}_{a}} \cdot {\mathbf{n}} = {{{\mathbf{v}}}_{b}} \cdot {\mathbf{n}},\quad {\mathbf{f}}_{n}^{a} = - {\mathbf{f}}_{n}^{b},\quad {\mathbf{f}}_{\tau }^{a} = {\mathbf{f}}_{\tau }^{b} = 0.$

Аналогичное условие использовалось на контакте верхнего слоя грунта и воды.

КРИТЕРИЙ РАЗРУШЕНИЯ

Рассматривается возможность разрушения в каждой точке области интегрирования. Применялся критерий Мизеса [11]:

${{T}_{{mises}}} = \frac{1}{{\sqrt 2 }}\sqrt {{{{({{T}_{{xx}}} - p)}}^{2}} + {{{({{T}_{{yy}}} - p)}}^{2}} + {{{({{T}_{{zz}}} - p)}}^{2}} + 2{{T}_{{xy}}}^{2} + 2{{T}_{{xz}}}^{2} + 2{{T}_{{yz}}}^{2}} > {{y}_{s}},$
где $p = \frac{{{{T}_{{xx}}} + {{T}_{{yy}}} + {{T}_{{zz}}}}}{3}$ – среднее напряжение, ys – предельное сдвиговое напряжение, значение которого для льда составляет 1 МПа.

МОДЕЛЬ БУРА

Современные буры имеют довольно сложное устройство, сочетающее ударные и вращательные механизмы. Нас в первую очередь интересует волновая картина, возникающая при бурении. Поэтому для простоты влияние бура представляется в качестве точечного источника с импульсом Риккера частотой 30 Гц. Его можно записать как

$R(t) = A(1 - 2{{\pi }^{2}}{{f}^{2}}{{t}^{2}}){\text{exp}}( - {{\pi }^{2}}{{f}^{2}}{{t}^{2}}),$
где A – коэффициент сжатия, f – чистота.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ УДАРОВ БУРА

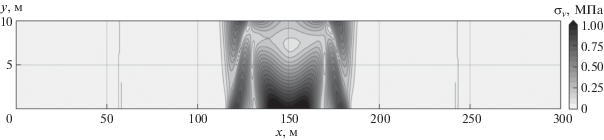
Был изучен процесс распространения волн при бурении, распределение напряжений в ледовом острове и его устойчивость к разрушению. На рис. 2 показано распределение напряжений Мизеса в момент времени t = 0.0325 с с начала бурения.

Рис. 2.

Распределение напряжений Мизеса при воздействии бура.

Опытным путем было установлено, что остров начинает разрушаться при амплитуде импульса волны, вызванной ударом бура, равной 1012 Па. Это значение слишком велико и не может быть в реальных условиях.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ СТАТИЧЕСКОЙ НАГРУЗКИ

Для решения задачи распределения статической нагрузки был использован метод установления [12]. Распределение напряжений считалось устойчивым, если модуль скорости распространения упругих волн оказывается в 20–30 раз ниже по сравнению со скоростью в начальный момент.

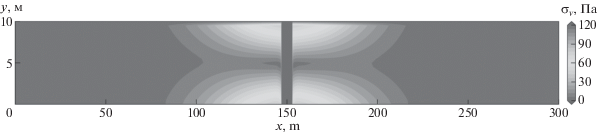
После завершения 200 тысяч шагов модуль скорости уменьшился примерно в 33 раза. Таким образом, полученное распределение напряжений можно считать устойчивым. Распределение напряжений Мизеса для устойчивого состояния представлено на рис. 3.

Рис. 3.

Распределение напряжений Мизеса при воздействии статической нагрузки.

Максимальное напряжение Мизеса в задаче составило 2.2 кПа. Эта величина меньше предельного сдвигового напряжения для льда. Таким образом, при реальных значениях статической нагрузки лед не разрушается.

Список литературы

  1. Crawford A., Crocker G., Mueller D., et al. The canadian ice island drift, deterioration and detection (CI2D3) database // J. of Glaciology. 2018. V. 64. № 245. P. 517–521.

  2. Petrov I.B. Problems of Modeling Natural and Anthropogenic Processes in the Arctic Zone of the Russian Federation // Mathematical Models and Computer Simulations. 2019. V. 11. P. 226–246.

  3. Xunqiang Y., Jianbo L., Chenglin W., et al. ANSYS implementation of damping solvent stepwise extraction method for nonlinear seismic analysis of large 3-D structures // Soil Dynamics and Earthquake Engineering. 2013. V. 44. P. 139–152.

  4. Nikolic Z., Zivaljic N., Smoljanovic H., et al. Numerical modelling of reinforced concrete structures under seismic loading based on the finite element method with discrete inter element cracks // Earthquake Engineering & Structural Dynamics. 2017. V. 46. № 1. P. 159–178.

  5. Moczo P., Robertsson J.O., Eisner L. The finite-difference time-domain method for modeling of seismic wave propagation // Advances in Geophysics. 2007. V. 48. P. 421–516.

  6. Komatitsch D., Tromp J. Introduction to the spectral element method for three-dimensional seismic wave propagation // Geophysical J. Intern. 1999. V. 139. № 3. P. 806–822.

  7. Wilcox L.C., Stadler G., Burstedde C., et al. A high-order discontinuous Galerkin method for wave propagation through coupled elastic-acoustic media // J. Computational Physics. 2010. V. 229. № 24. P. 9373–9396.

  8. De Basabe J., Mrinal S., Wheeler M. The interior penalty discontinuous Galerkin method for elastic wave propagation: grid dispersion // Geophysical J. Intern. 2008. V. 175. № 1. P. 83–93.

  9. Favorskaya A.V., Breus A.V., Galitskii B.V. Application of the grid-characteristic method to the seismic isolation model // Smart Innovation, Systems and Technologies. 2019. V. 133. P. 167–181.

  10. Petrov I.B., Muratov M.V. Application of the Grid-Characteristic Method to the Solution of Direct Problems in the Seismic Exploration of Fractured Formations (Review) // Mathematical Models and Computer Simulations. 2019. V. 11. P. 924–939.

  11. Grigorievih D.P., Khokhlov N.I., Petrov I.B. Calculation of dynamic destruction in deformable bodies // Matem. Mod. 2017. V. 29. № 4. P. 45–58.

  12. Fedorenko R.P. A relaxation method for solving elliptic difference equations // USSR Computational Mathematics and Mathematical Physics. 1962. V. 1. № 4. P. 1092–1096.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал