Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 69-73

ВОПРОСЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ВИБРАЦИОННОГО ГОРЕНИЯ

Е. В. Радкевич^1, 2, *, Н. Н. Яковлев^2, 3, **, О. А. Васильева^4, 5, ***

¹ Московский государственный университет имени М.В. Ломоносова
Москва, Россия

² Тураевское машиностроительное конструктурское бюро “Союз”
Лыткарино, Московская обл., Россия

³ Федеральный исследовательский центр химической физики им. Н.Н. Семенова Российской академии наук
Москва, Россия

⁴ Национальный исследовательский Московский государственный строительный университет
Москва, Россия

⁵ Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

^* E-mail: evrad07@gmail.com
^** E-mail: amntksoyuz@mail.ru
^*** E-mail: vasiljeva.ovas@yandex.ru

Поступила в редакцию 01.10.2020
После доработки 01.10.2020
Принята к публикации 05.10.2020

DOI: 10.31857/S2686954320060144

Полный текст (PDF)

Аннотация

Опираясь на термодинамический анализ процесса горения, построена новая модель ламинарного процесса вибрационного горения. Смоделированы два режима – детонационный и дефлаграционный, установлена природа их зарождения в зависимости от структуры стандартного химического потенциала и приведены численные эксперименты возникновения этих режимов. При управлении скоростью пассивной компоненты на входе, в зависимости от структуры стандартного химического потенциала, возникают высокочастотные колебания, приводящие к blow up.

Ключевые слова: термодинамический анализ, математические модели процесса горения, локальное равновесие, ламинарный процесс горения, высокочастотные колебания

В этой работе, опираясь на термодинамический анализ (см. [2–4]) процесса горения, мы построим новую модель ламинарного процесса вибрационного горения. Будут смоделированы детонационный и дефлаграционный режимы (см. [5–8]), установлена природа их зарождения в зависимости от структуры стандартного химического потенциала и приведены численные эксперименты возникновения режимов.

Мы рассматриваем идеализированную модель процесса горения, моделируется задача для открытой системы с обменом массой с внешней средой. Для такой системы возможно изменение молекулярной массы реагирующих компонентов, однако предполагается, что эти изменения настолько малы, что можно считать молекулярную массу постоянной. Учет переменной молекулярной массы приведет к не столь сложным изменениям в термодинамическом анализе процесса горения, при этом он уточнит выражение для энтропии. Представленный анализ проведен для простейшего случая идеального газа с постоянными теплоемкостью и молекулярной массой, что влечет выбор фиксированной постоянной адиабаты и входящая в расчеты газовая постоянная также является константой. Основной задачей статьи является формализация возникающих при горении обратных связей, приводящих к резонансу, описанному Раушенбахом [10].

Глобальную неоднородность системы можно характеризовать как неоднородное распределение энтальпии по потоку. Неоднородное распределение энтальпии по потоку отражает тот факт, что в модели $T = {\text{const}}$, $S = {\text{const}}$, когда нет ни источников, ни стоков тепла, единственной возможностью перетока накачиваемой кинетической энергии является образование вихрей. Ниже, для термодинамического анализа вибрационного горения, мы должны исследовать процесс, когда есть источники и стоки теплоты, т.е. теплота участвует в формировании хаотической вихревой структуры потока (“механизм Крокко”) и вихревая структура путем диссипации дает вклад в теплоту потока (“механизм Ричардсона”). Эти механизмы мы должны учесть ниже, учесть их вклад в глобальную неоднородность смеси при горении, характеризующуюся неоднородностью распределения энтальпии по потоку. Мы начнем наши исследования процесса вибрационного горения по возможности с простого, но содержательного с точки зрения физики примера двухкомпонентной смеси, на котором можно проверить возможность реализации в этом случае методов [2] математического моделирования критических явлений.

Термодинамический анализ вибрационного горения. Для одной активной компоненты глобальную неоднородность системы можно характеризовать как неоднородное распределение энтальпии по потоку (смеси). В этом случае процесс горения в фазовом пространстве переменных (V, $P$, T, $n$, $S$, $E$) приращение энтальпии

$\Delta H = (\gamma - 1)dE - PdV + TdS + \mu dn$

не есть полный дифференциал. Здесь $n$ – масса активной компоненты, $P$, T, S – давление, температура и энтропия, V – удельный объем, плотность $\varrho = \tfrac{1}{V}$, $\mu $ – химический потенциал. Используя плотность $\varrho $ как интегрирующий множитель (рассмотрев плотность приращения энтальпии $\frac{{\Delta H}}{V} = \varrho \Delta H$), получим

$\varrho \Delta H = d\left( {(\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\varrho + T\varrho S + n\varrho \mu } \right) + $

$\begin{gathered} + \;\varrho \left[ {\left( {(\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\varrho + TS\varrho + n\varrho \mu - P} \right)} \right] \times \\ \times \;dV - \varrho SdT - n\varrho d\mu . \\ \end{gathered} $

Введем приведенное давление

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} = P - \left( {(\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\varrho + TS\varrho + n\varrho \mu } \right)$

и его плотность

$\mathcal{P} = \frac{{\hat {P}}}{V} = \varrho \hat {P}.$

Как мы покажем ниже, $\hat {P}$ – давление процесса горения в смеси в состоянии покоя. Положим

(1)

$\mu = {{\mu }_{0}}(T) + RTln\left( {\frac{\mathcal{P}}{{{{\mathcal{P}}_{0}}}}} \right),$

${{\mu }_{0}}(T)$ – стандартное значение химического потенциала. Тогда

$\varrho \Delta H = d\left( {(\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\varrho + T\varrho S + n\varrho \mu - \hat {P}} \right) + $

$\begin{gathered} + \;\left( {V - \frac{{RnT\varrho }}{\mathcal{P}}} \right)d\mathcal{P} - \\ - \;\varrho \left( {S + n\left( {\frac{{d{{\mu }_{0}}(T)}}{{dT}} + Rln\left( {\frac{\mathcal{P}}{{{{\mathcal{P}}_{0}}}}} \right)} \right)} \right)dT. \\ \end{gathered} $

Приравнивая к нулю коэффициент при dT, получим уравнение состояния для энтропии

(2)

$S + n\left( {\frac{{d{{\mu }_{0}}(T)}}{{dT}} + Rln\left( {\frac{{nT{{\varrho }^{2}}}}{{{{n}_{0}}{{T}_{0}}\varrho _{0}^{2}}}} \right)} \right) = 0.$

Приравнивая к нулю коэффициент при $d\mathcal{P}$, получим уравнение состояния

$V - \frac{{RnT\varrho }}{\mathcal{P}} = 0 \Rightarrow \mathcal{P} = RnT{{\varrho }^{2}},$

для плотности давления P_G и адиабату Гюгонио для него самого:

$\hat {P} = RnT\varrho \,{\text{.}}$

Отсюда

$(\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\varrho + TS\varrho + n\varrho \mu - P + RnT\varrho = 0.$

Вставляя выражение (2) для S и μ = μ₀(T) + + $TR{\text{ln}}\left( {\tfrac{{nT{{\varrho }^{2}}}}{{{{n}_{0}}{{T}_{0}}\varrho _{0}^{2}}}} \right)$, получим для давления P модификацию адиабаты гидродинамической неустойчивости (см. [2])

(3)

$\begin{gathered} P = (\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\varrho + \\ + \left( { - T\frac{{d{{\mu }_{0}}(T)}}{{dT}} + {{\mu }_{0}}(T) + RT} \right)n\varrho = \\ \end{gathered} $

$ = \;{{P}_{A}} + {{P}_{G}} + \left[ { - T\frac{{d{{\mu }_{0}}(T)}}{{dT}} + {{\mu }_{0}}(T)} \right]n\varrho ,$

где ${{P}_{A}} = (\gamma - 1)\varrho E + \tfrac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\varrho $ – давление гидродинамического процесса, ${{P}_{G}} = RTn\varrho $ процесса горения без учета влияния гидродинамического процесса (тепловая теория). Здесь P_{A, G} = $\left[ { - T\tfrac{{d{{\mu }_{0}}(T)}}{{dT}} + {{\mu }_{0}}(T)} \right]n\varrho $ – вклад в давление, порожденный взаимодействием процесса горения и адиабатического гидродинамического процесса.

Энергия завихренности

Из (2), (3) следует, что в фазовом пространстве переменных ($n$, $P$, E, $\varrho $, S, $T$) соотношения (2), (3) определяют многообразие ${{\mathcal{M}}_{V}}$ локального равновесия, на котором плотность приращения энтальпии есть полный дифференциал:

(4)

$\varrho \Delta H = d{{H}_{{\mathcal{M},V}}},$

где

${{H}_{{\mathcal{M},V}}} = (\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}(\varrho - {{\varrho }_{0}}) + T\varrho S + n\varrho \mu - \hat {P} - $

(5)

$ - \;{{T}_{0}}{{\varrho }_{0}}{{S}_{0}} - {{n}_{0}}{{\varrho }_{0}}{{\mu }_{0}} + {{(\hat {P})}_{0}} = $

$\begin{gathered} = \;(\gamma - 1)\varrho E + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}(\varrho - {{\varrho }_{0}}) + \\ + \;\left[ { - T\frac{{d{{\mu }_{0}}(T)}}{{dT}} + {{\mu }_{0}}(T) - RT} \right]n\varrho - \\ \end{gathered} $

$ - \;\left[ { - {{T}_{0}}\frac{{d{{\mu }_{0}}({{T}_{0}})}}{{dT}} + {{\mu }_{0}}({{T}_{0}}) - R{{T}_{0}}} \right]{{n}_{0}}{{\varrho }_{0}} = $

$ = \;{{P}_{A}} - {{P}_{G}} + {{P}_{{A,G}}} - {{({{P}_{A}})}_{0}} + {{({{P}_{G}})}_{0}} - {{({{P}_{{A,G}}})}_{0}}$

есть энергия завихренности (см. [2]).

Модель ламинарного вибрационного горения. Учитывая систему соотношений (2), (3) модель ламинарных пламен (на многообразии локального равновесия $\mathcal{M}$) можно описать системой уравнений механики сплошной среды (уравнения Эйлера и уравнения диффузии и теплопроводности). В безразмерных переменных $S = {{S}_{ * }}\widetilde S$, $T = {{T}_{ * }}\tilde {T}$, $n = {{n}_{ * }}\tilde {n}$, $P = {{P}_{ * }}\tilde {P}$, $V = {{V}_{ * }}\tilde {V}$, ${{P}_{ * }}$ = ${{({{P}_{A}})}_{ * }}$ + ${{({{P}_{G}})}_{ * }}$ + $\left( { - {{T}_{*}}\frac{{d{{\mu }_{0}}({{T}_{*}})}}{{dT}} + {{\mu }_{0}}({{T}_{*}})} \right){{n}_{*}}{{\varrho }_{*}}$, ${{S}_{ * }}$ = $ - {{n}_{ * }}\tfrac{{d{{\mu }_{0}}({{T}_{ * }})}}{{dT}}:$

(6)

${{\partial }_{{\tilde {t}}}}\tilde {\varrho } + {{\partial }_{{\tilde {x}}}}(\tilde {\varrho }\tilde {U}) = 0,$

${{\partial }_{{\tilde {t}}}}((1 - {{c}_{ * }}\tilde {n})\tilde {\varrho }{{\tilde {u}}_{2}}) + {{\partial }_{{\tilde {x}}}}((1 - {{c}_{ * }}\tilde {n})\tilde {\varrho }\tilde {u}_{2}^{2}) + {{\partial }_{{\tilde {x}}}}\tilde {P} = 0,$

${{\partial }_{{\tilde {t}}}}({{c}_{ * }}\tilde {n}\tilde {\varrho }\mathop {\widetilde u}\nolimits_1 ) + {{\partial }_{x}}({{c}_{ * }}\tilde {n}\tilde {\varrho }\tilde {u}_{1}^{2}) + {{\partial }_{{\tilde {x}}}}\tilde {P} = 0,$

$\tilde {\varrho }\frac{d}{{d\tilde {t}}}\tilde {E} + \tilde {P}\widetilde {{\text{div}}}\tilde {U} = 0,$

средняя скорость смеси $\tilde {U} = {{c}_{0}}\tilde {n}{{\tilde {U}}_{1}} + (1 - {{c}_{0}}\tilde {n}){{\tilde {U}}_{2}}$,

(7)

$\tilde {\varrho }\tilde {c}\frac{d}{{dt}}\tilde {T} = {{\partial }_{{\tilde {x}}}}(\tilde {\lambda }{{\partial }_{{\tilde {x}}}}\tilde {T}) + \tilde {T}\tilde {S}\tilde {W}(\tilde {n},\tilde {T}),$

$\tilde {\varrho }\frac{d}{{dt}}\tilde {n} = {{\partial }_{{\tilde {x}}}}(\tilde {\varrho }\tilde {D}{{\partial }_{{\tilde {x}}}}\tilde {n}) - \tilde {W}(\tilde {n},\tilde {T})$

(8)

$\tilde {W} = {{\tilde {k}}_{0}}\tilde {\varrho }{{\tilde {n}}^{\beta }}{{e}^{{ - \tfrac{{\mathop {\widetilde E}\nolimits_ * }}{{R\widetilde T}}}}},$

β – порядок реакции ($\beta = 0,\;1,\;2$), ${{\tilde {E}}_{*}}$ – энергия активации формулы Арениуса (8) для скорости [9]. Замыкающие уравнения

(9)

$\begin{gathered} \tilde {P} = (\gamma - 1)\tilde {\varrho }\tilde {E} + \frac{{{{P}_{0}}}}{{{{\varrho }_{0}}}}\tilde {\varrho } + \\ + \;\left( { - \tilde {T}\frac{{d{{{\tilde {\mu }}}_{0}}(\tilde {T})}}{{d\widetilde T}} + {{{\tilde {\mu }}}_{0}}(\tilde {T}) + R\tilde {T}} \right)\tilde {n}\tilde {\varrho }, \\ \end{gathered} $

$\tilde {S} + \tilde {n}\left( {\frac{{d{{{\tilde {\mu }}}_{0}}(\tilde {T})}}{{d\tilde {T}}} + Rln\left( {\frac{{\tilde {n}\tilde {T}{{{\tilde {\varrho }}}^{2}}}}{{{{{\tilde {n}}}_{0}}{{{\tilde {T}}}_{0}}\tilde {\varrho }_{0}^{2}}}} \right)} \right) = 0.$

Численный эксперимент модели (6)–(8).

Для определения режимов дефлаграционного и детонационного горения проведем численные эксперименты модели (6)–(8) на отрезке $\tilde {x} \in [0,\;1]$ с граничным условием замкнутой системы

$\begin{gathered} {{\partial }_{{\tilde {x}}}}{{\left. {\tilde {\varrho }} \right|}_{{\tilde {x} = 0}}} = {{\partial }_{{\tilde {x}}}}{{\left. {\tilde {\varrho }} \right|}_{{\tilde {x} = 1}}} = {{\partial }_{{\tilde {x}}}}{{\left. {{{{\tilde {u}}}_{1}}} \right|}_{{\tilde {x} = 0}}} = \\ = \;{{\partial }_{{\tilde {x}}}}{{\left. {{{{\tilde {u}}}_{1}}} \right|}_{{\tilde {x} = 1}}} = {{\partial }_{{\tilde {x}}}}{{\left. {{{{\tilde {u}}}_{2}}} \right|}_{{\tilde {x} = 0}}} = {{\partial }_{{\tilde {x}}}}{{\left. {{{{\tilde {u}}}_{2}}} \right|}_{{\tilde {x} = 1}}} = 0, \\ \end{gathered} $

(10)

${{\partial }_{{\tilde {x}}}}{{\left. {\tilde {T}} \right|}_{{\tilde {x} = 0}}} = {{\partial }_{{\tilde {x}}}}{{\left. {\tilde {T}} \right|}_{{\tilde {x} = 1}}} = {{\partial }_{{\tilde {x}}}}{{\left. {\tilde {n}} \right|}_{{\tilde {x} = 0}}} = {{\partial }_{{\tilde {x}}}}{{\left. {\tilde {n}} \right|}_{{\tilde {x} = 1}}} = 0$

и начальными условиями, моделирующими в одномерном случае впрыскивание из форсунки горючей компоненты двухкомпонентной смеси:

${{\left. {\tilde {\varrho }} \right|}_{{\widetilde t = 0}}} = {{\tilde {\varrho }}_{0}} = 1,\quad {{\left. {{{{\tilde {u}}}_{1}}} \right|}_{{\widetilde t = 0}}} = \tilde {u}_{1}^{0} = 0.2,$

(11)

${{\left. {{{{\tilde {u}}}_{2}}} \right|}_{{\widetilde t = 0}}} = \tilde {u}_{2}^{0} = 0.2,\quad {{\left. {\tilde {T}} \right|}_{{\tilde {t} = 0}}} = {{\tilde {T}}_{0}} = 10$

константы, ${{\left. {\tilde {n}} \right|}_{{t = 0}}} = {{n}_{1}} = 0.5$, $\tilde {x} \in (0,0.3) \cup (0.4,0.5)$, ${{\left. {\tilde {n}} \right|}_{{\tilde {t} = 0}}}$ = 0.66, $\tilde {x} \in (0.3,\;0.4)$, ${{\tilde {E}}_{*}} = 10$. Начальные данные для внутренней энергии ${{\tilde {E}}_{0}} = 1$.

Детонация и дефлаграция в вибрационном горении.

Выше мы выдвинули гипотезу, что возникновение режимов дефлаграции и детонации связано со структурой стандартного химического потенциала ${{\tilde {\mu }}_{0}}(T)$. Расчеты привязаны к разным структурам функции ${{\tilde {\mu }}_{0}}$. Ниже приведены графики временных сечений решения модели (6)–(8).

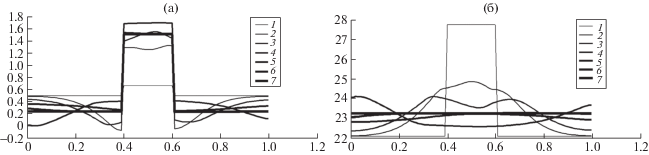
Характерное поведение графиков решения смешанной задачи (6)–(11) зависит от структуры производной $\tfrac{d}{{d\widetilde T}}{{\tilde {\mu }}_{0}}(\tilde {T})$. В примере (см. рис. 1) для

${{\tilde {\mu }}_{0}}(\tilde {T})$ = ${{\tilde {T}}_{0}}\left[ {{{B}_{ * }} - (R + {{A}_{ * }})\tfrac{{{{{\tilde {T}}}^{4}}}}{{\tilde {T}_{0}^{4}}}} \right],$

(12)

$\frac{d}{{d\widetilde T}}{{\tilde {\mu }}_{0}}(\tilde {T}) = - 4(R + {{A}_{ * }})\frac{{{{{\tilde {T}}}^{3}}}}{{\tilde {T}_{0}^{3}}},$

температура $\tilde {T}$ растет, приведенное количество вещества первой компоненты $\tilde {n}$ убывает, энтропия и давление сначала убывают, затем меняют выпуклость и возрастают, стабилизируясь при t → ∞ к однородному состоянию, т.е. мы имеем детонационный характер процесса горения.

Рис. 1.

a – временные сечения для приведенного количества вещества активной компоненты $\tilde {S}$ для t = 0 (1); 0.008 (2); 0.016 (3); 0.04 (4); 0.08 (5); 0.12 (6); 0.16 (7); б – временные сечения для давления $\tilde {P}$ для t = 0 (1); 0.008 (2); 0.016 (3); 0.04 (4); 0.08 (5); 0.12 (6); 0.16 (7).

Акустические колебания. Приведем цитату Раушенбаха из [10]: “При вибрационном горении возникают высокочастотные колебания в камере сгорания Они могут существенно нарушить процесс горения и привести к разрушению конструкции двигателя. Эти колебания связаны с взаимодействием горения и акустических колебаний газового столба, заключенного в двигателе”. В этом разделе мы смоделируем процесс, описанный Раушенбахом.

Численный эксперимент модели (6)–(8). Мы приведем результаты численного эксперимента, подтверждающие справедливость утверждения Раушенбаха из [10]. Численный эксперимент модели (6)–(8) на отрезке $\tilde {x} \in [0,\;1]$ с граничным условием, включающим управление потоком нейтральной компоненты на входе:

(13)

${{\left. {{{{\tilde {q}}}_{2}}} \right|}_{{\tilde {x} = 0}}} = \tilde {q}_{2}^{0}(0) + K\tilde {t},$

(14)

$\begin{gathered} {{\partial }_{{\tilde {x}}}}{{\left. {\tilde {\varrho }} \right|}_{{\widetilde x = 0}}} = {{\partial }_{{\tilde {x}}}}{{\left. {\tilde {\varrho }} \right|}_{{\tilde {x} = 1}}} = {{\partial }_{{\tilde {x}}}}{{\left. {{{{\tilde {u}}}_{1}}} \right|}_{{\tilde {x} = 0}}} = \\ = \;{{\partial }_{{\tilde {x}}}}{{\left. {{{{\tilde {u}}}_{1}}} \right|}_{{\tilde {x} = 1}}} = {{\partial }_{{\tilde {x}}}}{{\left. {{{{\tilde {u}}}_{2}}} \right|}_{{\tilde {x} = 1}}} = 0, \\ \end{gathered} $

(15)

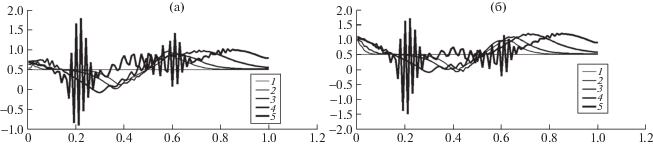
$\begin{gathered} {{\left. {\tilde {\varrho }} \right|}_{{\tilde {t} = 0}}} = {{{\tilde {\varrho }}}_{0}} = 1,\quad {{\left. {{{{\tilde {u}}}_{1}}} \right|}_{{\tilde {t} = 0}}} = \tilde {u}_{1}^{0} = 0.2, \\ {{\left. {{{{\tilde {u}}}_{2}}} \right|}_{{\tilde {t} = 0}}} = \tilde {u}_{2}^{0} = 0.2, \\ \end{gathered} $

${{\left. {\tilde {T}} \right|}_{{\tilde {t} = 0}}} = {{\tilde {T}}_{0}} = 10,$

${{\left. {\tilde {n}} \right|}_{{\tilde {t} = 0}}} = {{n}_{1}}$ = 0.5, $\tilde {x} \in (0,\;0.3) \cup (0.4,\;0.5)$, ${{\left. {\tilde {n}} \right|}_{{\tilde {t} = 0}}} = 0.66$, $\tilde {x} \in (0.3,0.4)$, ${{\tilde {E}}_{*}} = 100$. Начальные данные для внутренней энергии ${{\tilde {E}}_{0}} = 1$. Поведение графиков решения смешанной задачи (7)–(8), (13)–(15) зависит от структуры производной $\tfrac{d}{{d\widetilde T}}{{\tilde {\mu }}_{0}}(\tilde {T})$. В случае

$\mathop {\tilde {\mu }}\nolimits_0 (\tilde {T}) = {{\tilde {T}}_{0}}\left[ {{{B}_{ * }} - (R + {{A}_{ * }})\frac{{{{{\tilde {T}}}^{5}}}}{{\tilde {T}_{0}^{5}}}} \right]$

в численном эксперименте для значения ${{A}_{ * }} + R$ = = 5.5, меньше критического $A_{ * }^{{cr}} + R = 7$, возникают высокочастотные колебания, достаточно быстро разрушающиеся во времени. Процесс стремится к однородному состоянию. Отметим, что зарождение высокочастотных осцилляций возникает при возрастании давления в окрестностях максимума и минимума скорости пассивной компоненты. Здесь ${{B}_{ * }} = 7.5$, скорость нарастания потока пассивной компоненты на входе K = 0.1 (см. (13)), сечения начального счета: t = 0; $0.002$; 0.004; 0.02; 0.05; 0.1; 0.2.

Ниже (см. рис. 2) для того же ${{\tilde {\mu }}_{0}}(\tilde {T})$ приведем численный эксперимент со значением параметра ${{A}_{ * }} + R$ = 6.95, близким к критическому $A_{ * }^{{cr}} + R$ = 7, что приведет к blow up. Как и выше, K = 0.1 – коэффициент увеличения ${{\tilde {q}}_{2}}$ (см. (13)), cечения начального счета $t = 0;0.002;0.004;0.01;0.02$ и ${{B}_{ * }} = 7$.

Рис. 2.

a – Временные сечения для скорости активной компоненты ${{\tilde {u}}_{1}}$ для t = 0 (1); 0.002 (2); 0.004 (3); 0.01 (4); 0.02 (5); б – временные сечения для скорости пассивной компоненты ${{\tilde {u}}_{2}}$ для t = 0 (1); 0.002 (2); 0.004 (3); 0.01 (4); 0.02 (5).

Заключение. Как мы отмечали выше, глобальную неоднородность системы можно характеризовать как неоднородное распределение энтальпии по двухкомпонентной смеси. В этом случае для процесса горения в фазовом пространстве переменных ($\varrho $, P, T, $n$, $S$, $E$) приращение энтальпии не есть полный дифференциал. Приращение энтальпии есть полный дифференциал на многообразие локального равновесия $\mathcal{M}$ (ламинарного процесса горения). Такие утверждения позволили выделить в фазовом пространстве соответствующую адиабату процесса горения (адиабату Гюгонио) и уравнение для энтропии. Эти два уравнения состояния замыкают классическую математическую модель процесса горения: (6)–(8). Выше, численным экспериментом, мы показали, что два режима процесса горения – дефлаграция и детонация определяются структурой μ₀(T) – стандартного значения химического потенциала. Более того, при управлении скоростью пассивной компоненты на входе, в зависимости от структуры μ₀(T), возникают высокочастотные колебания, приводящие к blow up. Хорошо известны (см. [9]) режимы осцилляции, которые демонстрирует зависимость температуры от времени при горении углеводородов [9]. Различные режимы горения углеводородов рассмотрены в [11].

ИСТОЧНИК ФИНАНСИРОВАНИЯ

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 18-01-00524).

Список литературы

Радкевич Е.В., Яковлев Н.Н., Васильева О.А., Сидоров М.И., Ставровский М. О возможности приложения теории Кана–Хилларда к математическому моделированию процесса горения. М.: Эко-Пресс, 2020. 188 с.
Радкевич Е.В., Лукашев Е.А., Яковлев Н.Н., Васильева О.А., Сидоров М.И. Введение в обобщенную теорию неравновесных фазовых переходов и термодинамический анализ задач механики сплошной среды. М.: Изд-во Моск. ун-та, 2019. 342 с.
Радкевич Е.В., Лукашев Е.А., Васильева О.А. Гидродинамические неустойчивости и неравновесные фазовые переходы (в форме Кана–Хилларда) // ДАН. 2019. Т. 486. № 5. С. 17–22.
Радкевич Е.В., Васильева О.А., Сидоров М.И. Кристаллизация бинарных сплавов и неравновесные фазовые переходы // ДАН. 2019. Т. 489. № 6. С. 11–17.
Frolov S.M, Ivanov V.S. Deflagrative and Detonative Combust / Eds. G.D. Roy, S.M. Frolov. 2010. P. 133.
Беляев А.А., Басевич В.Я., Фролов Ф.С., Фролов С.М., Басара Б., Суффа М. Горение и взрыв. Под ред. С.М. Фролова М.: Торус Пресс, 2010. Вып. 3. С. 30.
Reitz R.D. Mechanism of Atomization Processes in High Pressure Vaporizing Spray // Atomization and Spray Technology. 1987. V. 3. P. 309–337.
Lee C.H., Reitz R.D. An experimental study of the effect of gas density on the distortion and breakup mechanism of drops in high speed gas stream // Int. J. of Multiphase Flow. 2000. V. 26. P. 229–244.
Ксандопуло Г.И., Дубинин В.В. Химия газофазного горения. М.: Химия, 1987. 341 с.
Раушенбах Б.В. Вибрационное горение. М.: Гос. изд. физ.-мат. лит., 1961. 500 с.
Щетинков Е.С. Физика горения газов. М.: Наука, 1965. 739 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал