Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 100-106

1. СООТНОШЕНИЕ МЕЖДУ α-МНОЖЕСТВАМИ И СЛАБО ВЫПУКЛЫМИ МНОЖЕСТВАМИ ПО ЕФИМОВУ–СТЕЧКИНУ

Будем использовать следующие обозначения.

Через coM обозначим выпуклую оболочку множества M, clM – замыкание множества M, $\left\langle {{{x}_{ * }},x{\text{*}}} \right\rangle $ – скалярное произведение ${{x}_{ * }}$ и $x{\text{*}}$ из ${{\mathbb{R}}^{n}}$, $\left\| {{{x}_{ * }}} \right\| = {{\left\langle {{{x}_{ * }},{{x}_{ * }}} \right\rangle }^{{1/2}}}$ – евклидову норму в ${{\mathbb{R}}^{n}}$, diam(M) = = $\mathop {sup}\limits_{x,y \in M} \left\| {x - y} \right\|$ – диаметр множества M, B(a, r) = = $\{ x\, \in \,{{\mathbb{R}}^{n}}\,:\,\left\| {x\, - \,a} \right\|\, < \,r\} $ – открытый шар радиуса r и с центром в точке a, $\angle ({{x}_{ * }},x*)$ = ${\text{arccos}}\frac{{\langle {{x}_{ * }},x{\text{*}}\rangle }}{{\left\| {{{x}_{ * }}} \right\| \cdot \left\| {x{\text{*}}} \right\|}}\, \in \,[0,\pi ]$ – угол между векторами ${{x}_{ * }}$ и x*.

Под метрической проекцией $p{\text{*}}$ точки x* на множество M мы понимаем ближайшую к x* точку из M. Множество всех проекций точки x* на множество M обозначим через ${{\Omega }_{M}}(x*)$.

В частном случае $\alpha $-множества из двумерного евклидового пространства его можно определить следующим образом [10].

Определение 1. Пусть A – замкнутое множество в двумерном евклидовом пространстве ${{\mathbb{R}}^{2}}$ и $z* \in {{\mathbb{R}}^{2}}{\backslash }A$. Определим функцию

и

Полагаем ${{\alpha }_{A}} = \mathop {sup}\limits_{z* \in {{\mathbb{R}}^{n}}\backslash A} {{\alpha }_{A}}(z*) \in [0,\pi ]$.

Множество A с мерой невыпуклости $\alpha = {{\alpha }_{A}}$ назовем α-множеством.

Отметим, что в евклидовых пространствах размерности 3 и выше α-множества определены иначе (см. [1, 10]), но в ${{\mathbb{R}}^{2}}$ все определения эквивалентны [10, теорема 1].

Определение 2 [11]. Множество A в линейном пространстве E называется  слабо выпуклым по Ефимову–Стечкину, с постоянной R > 0, если существует непустое множество ${{A}_{1}} \subset E$ такое, что

Определение 3 [2, §1.1]. Пусть в линейном пространстве E с нормой ${{\left\| {\; \cdot \;} \right\|}_{E}}$ заданы две точки x, y и задано число $R \geqslant \frac{{{{{\left\| {x - y} \right\|}}_{E}}}}{2}$. Множество

называется сильно выпуклым отрезком.

Определение 4 [2, §1.1]. Множество A в линейном пространстве E с нормой ${{\left\| {\; \cdot \;} \right\|}_{E}}$ называется слабо выпуклым по Виалю с постоянной R > 0, если для любых двух точек $x,y \in A$ таких, что $0 < {{\left\| {x - y} \right\|}_{E}} < 2R$, существует точка $z \in {{D}_{R}}(x,y) \cap A$, не совпадающая с точками x и y.

Под расстоянием от точки x до множества M в линейном пространстве E с нормой ${{\left\| {\; \cdot \;} \right\|}_{E}}$ будем понимать величину $\rho (x,M) = \mathop {inf}\limits_{y \in M} {{\left\| {x - y} \right\|}_{E}}$.

Определение 5 [2, §1.7]. Будем говорить, что множество M в линейном пространстве E с нормой ${{\left\| {\; \cdot \;} \right\|}_{E}}$ обладает  чебышевским слоем толщины R > 0, если для любой точки $x \in E$ такой, что $\rho (x,M) < R$, существует и единственна метрическая проекция точки $x$ на M.

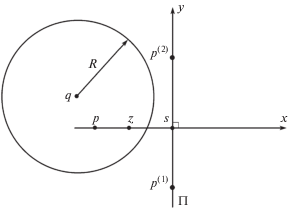
Лемма 1. Пусть заданы две точки p⁽¹⁾, p⁽²⁾на плоскости и число $R > \tfrac{{{\text{|}}{{p}^{{(1)}}}{{p}^{{(2)}}}{\text{|}}}}{2}$, где |p⁽¹⁾p⁽²⁾| = ${\text{||}}{{p}^{{(2)}}} - {{p}^{{(1)}}}{\text{||}}$ – длина отрезка p⁽¹⁾p⁽²⁾. Обозначим через $s = \frac{1}{2}$(p⁽¹⁾ + p⁽²⁾) середину отрезка p⁽¹⁾p⁽²⁾, через $ps$ серединный перпендикуляр к отрезку p⁽¹⁾p⁽²⁾, через $B(q,R)$ такой открытый круг с центром в точке q и радиусом R, что ${{p}^{{(1)}}} \notin B(q,R)$, ${{p}^{{(2)}}} \notin B(q,R)$. Пусть некоторая точка $z \in ps \cap B(q,R)$ (рис. 1).

Тогда, если $\left| {zs} \right| \geqslant R - \sqrt {{{R}^{2}} - \frac{1}{4}{\text{|}}{{p}^{{(1)}}}{{p}^{{(2)}}}{{{\text{|}}}^{2}}} $, то точки z и q лежат в одной полуплоскости относительно прямой $\Pi $, содержащей p⁽¹⁾и p⁽²⁾.

Доказательство. Введем декартову систему координат с центром в точке s, ось sy проведем через точку p⁽²⁾. Без ограничения общности считаем, что точка z находится слева от точки s, как показано на рис. 1.

Введем обозначения

где

Предположим противное, что точка q находится по другую сторону от прямой Π относительно точки z, т.е. ${{x}_{0}} > 0$. Покажем, что это невозможно.

Действительно, условия ${{p}^{{(1)}}} \notin B$(q, R) и ${{p}^{{(2)}}} \notin B$(q, R) равносильны системе неравенств

из которых (при ${{x}_{0}} > 0$) следует, что

С учетом (1), (2) и (3) получаем, что

т.е. $z$ не может принадлежать кругу $B(q,R)$.

Таким образом, пришли к противоречию.

Лемма 2. Пусть множество $A \subset {{\mathbb{R}}^{2}}$ слабо выпуклое по Ефимову–Стечкину с постоянной R, связно и его диаметр ${\text{diam}}(A) < 2R$.

Тогда A обладает чебышевским слоем толщины R.

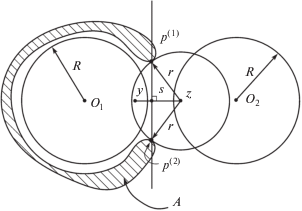
Доказательство проведем от противного. По определению 5 для наличия чебышевского слоя толщины R у множества A все точки, удаленные от A на расстояние, меньшее R, должны иметь единственную метрическую проекцию на A. Предположим, что существует точка $z \in {{\mathbb{R}}^{2}}{\backslash }M$ такая, что $\rho (z,A) < R$, и имеющая по крайней мере две различные метрические проекции p⁽¹⁾ и p⁽²⁾ на A. Обозначим через $r = {\text{||}}z - {{p}^{{(1)}}}{\text{||}}$. Заметим, что $r = \rho (z,A)$ < R и что в круге $B(z,r)$ не может быть ни одной точки из A.

Обозначим через $s = \tfrac{{{{p}^{{(1)}}} + {{p}^{{(2)}}}}}{2}$ и рассмотрим точку

Заметим (см. рис. 2), что

из-за монотонного убывания функции

f(r) = r ‒ $\sqrt {{{r}^{2}} - \frac{1}{4}{\text{|}}{{p}^{{(1)}}}{{p}^{{(2)}}}{{{\text{|}}}^{2}}} $ при $r > \frac{1}{2}{\text{|}}{{p}^{{(1)}}}{{p}^{{(2)}}}{\text{|}}$.

Следовательно, точка y находится в круге B(z, r), и, значит, $y \in {{\mathbb{R}}^{2}}{\backslash }A$. В силу слабой выпуклости по Ефимову–Стечкину множества A существует открытый круг радиуса R, который содержит точку y, но не пересекается с множеством A.

Однако

и, следовательно, в силу леммы 1, центр любого такого круга, содержащего точку y, но не содержащего точки p⁽¹⁾ и p⁽²⁾, будет находиться по одну сторону от прямой p⁽¹⁾p⁽²⁾ вместе с точкой y (т.е. находиться в одной полуплоскости, образуемой прямой p⁽¹⁾p⁽²⁾). Аналогично, центр любого открытого круга радиуса $R$, не пересекающегося с A, содержащего точку z, но не содержащего точки p⁽¹⁾ и p⁽²⁾, будет находиться по другую сторону от прямой p⁽¹⁾p⁽²⁾ относительно точки y (рис. 2).

Очевидно, что точки p⁽¹⁾ и p⁽²⁾ невозможно соединить какой-либо кривой из A, не нарушив условия ${\text{diam}}(A) < R$. Следовательно, нарушается условие связности A и наше предположение о существовании нескольких проекций неверно.

Теорема 1. Пусть связное множество $A \subset {{\mathbb{R}}^{2}}$ слабо выпукло по Ефимову–Стечкину с постоянной R и ${\text{diam}}(A) \leqslant 2r$, где $r < R$. Тогда A является α-множеством с числом

Доказательство. Прежде всего заметим, что, в силу [2, лемма 1.3.4], A является замкнутым, как и любое другое множество, слабо выпуклое по  Ефимову–Стечкину. Тем самым A является α-множеством с числом $\alpha \leqslant \pi $. Оценим степень его невыпуклости $\alpha $ более аккуратно.

Вначале докажем, что ни одна точка $z* \in {{\mathbb{R}}^{2}}{\backslash }A$ не может находиться в выпуклой оболочке своих проекций на множество A. Действительно, предположим, что существует такая точка $z* \in {\text{co}}{{\Omega }_{A}}(z*)$. Тогда множество проекций ${{\Omega }_{A}}(z*)$ должно содержать не менее двух точек. Однако, в силу леммы 2, множество A обладает чебышевским слоем толщины  R, или, иными словами, все точки из $R$-окрестности множества A обладают единственной метрической проекцией на A. Следовательно, расстояние $\rho (z*,{{\Omega }_{A}}(z*)) \geqslant R$ или, иначе говоря, точка z* является центром открытого круга $B(z*,\hat {R})$ с радиусом

который не содержит точек из A. В то же время на границе данного круга располагается множество ${{\Omega }_{A}}(z*)$. Если множество ${{\Omega }_{A}}(z*)$ содержит всего две проекции, то в силу соотношения $z* \in {\text{co}}{{\Omega }_{A}}(z*)$ эти проекции есть диаметрально противоположные точки круга $B(z*,\hat {R})$, расстояние между которыми $2\hat {R}$. Это противоречит неравенству ${\text{diam}}(A) \leqslant 2r$. Если множество ${{\Omega }_{A}}(z*)$ содержит большее количество точек, то можно выбрать из них такие точки x⁽¹⁾, x⁽²⁾, x⁽³⁾, что $z* \in {\text{co}}\{ {{x}^{{(1)}}},{{x}^{{(2)}}},{{x}^{{(3)}}}\} $. Однако несложными рассуждениями, учитывая линейную связность $A$, приходим к выводу, что данный случай также невозможен из-за неравенства ${\text{diam}}(A) \leqslant 2r$.

Итак, мы получили, что A является α-множеством с числом $\alpha < \pi $. Оценим теперь значение α, ссылаясь на определение 1. Пусть

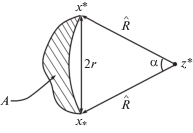
Рассмотрим $\Delta {{x}_{ * }}x{\text{*}}z{\text{*}}$ на рис. 3.

По теореме косинусов

Отсюда,

Так как ${{\Omega }_{A}}(z*) \subset A$, то

Поскольку функция (5) достигает максимума при наибольшем ${\text{|}}{{p}^{{(1)}}}{{p}^{{(2)}}}{\text{|}}$ и наименьшем $\hat {R}$, то из неравенств (6) и (4) следует утверждение теоремы.

2. ОСНОВНОЙ РЕЗУЛЬТАТ

Введем в рассмотрение управляемую систему на промежутке $[{{t}_{0}},\vartheta ]$, описываемую векторным дифференциальным уравнением

где $t$ – время, $x(t) \in {{\mathbb{R}}^{2}}$ – фазовый вектор, ${{X}^{{(0)}}}$ – ограниченное множество в ${{\mathbb{R}}^{2}}$, $u(t)$ – вектор управления из компакта $P \subset {{\mathbb{R}}^{2}}$, $f:[{{t}_{0}},T] \times {{\mathbb{R}}^{2}} \mapsto {{\mathbb{R}}^{2}}$ – непрерывная функция, $B(t)$ – (2 × 2)-матрица с непрерывными коэффициентами. Под множеством допустимых управлений U системы (7) понимаем множество всех интегрируемых по Лебегу вектор-функций $u(t){\text{:}}\;[{{t}_{0}},T] \mapsto P$.

Предполагаем выполненными следующие условия на систему (7):

1) для любого $t \in [{{t}_{0}},T]$ функция $f(t,x)$ дифференцируема по x,

2) производная $f_{x}^{'}( \cdot ,x)$ ограничена константой M и удовлетворяет условию Липшица с постоянной L,

3) множество X⁽⁰⁾ слабо выпукло по Ефимову–Стечкину с постоянной ${{R}_{0}} > \tfrac{1}{2}{\text{diam}}({{X}^{{(0)}}})$,

4) для любого $t \in [{{t}_{0}},T]$ множество B(t) · P = = ${\text{\{ }}B(t)u{\text{:}}\;u \in P{\text{\} }}$ сильно выпукло [2, определение 1.1.4] с постоянной ${{r}_{P}}$,

5) выполнено неравенство ${{r}_{P}} \leqslant M\hat {R}$, где

При этих условиях существуют решения x(t) системы в классе абсолютно непрерывных функций на $[{{t}_{0}},T]$, которые мы называем движениями системы (7).

Обозначим через $X(T) = X(T;{{t}_{0}},{{X}^{{(0)}}})$ множество достижимости системы (7) в конечный момент времени T со стартовым множеством X⁽⁰⁾. Относительно $X(T)$ сформулируем и докажем следующие утверждения.

Лемма 3. Справедлива оценка

Доказательство. Рассмотрим два произвольных движения $x(t)$ и $y(t)$ управляемой системы (7), порожденное допустимыми управлениям $u(t)$ и ${v}(t)$ соответственно, и оценим рассогласование $\left\| {y(T) - x(T)} \right\|$ этих движений в момент T, тем самым мы оценим ${\text{diam}}(X(T))$.

Из уравнения (7) следует, что для этих движений выполняется соотношение

которое после интегрирования по времени $t$ принимает вид

Учитывая сильную выпуклость множества $B(t) \cdot P$ и неравенство ${{r}_{P}} \leqslant M\hat {R}$ из условия 5), получаем, что

Кроме того, применив теорему об оценке конечных приращений (см., например, [12, гл. 1, §3.3, теорема 3.3.2]) для функции $f(t, \cdot )$, получаем для любого момента времени $t \in [{{t}_{0}},T]$ неравенство

Из (9), (10) и (11) следует оценка

Применяя к (12) лемму Гронуолла [13, гл. 1, §2, с. 26], получаем неравенство

которое выполняется, в частности, при t = T. В силу произвольности выбора движений $x(t)$ и $y(t)$ из него следует утверждение леммы.

Замечание 1. Для выполнения утверждения леммы 3 по отношению к системе (7) условие 3) излишне, а условия 4) и 5) можно заменить простым неравенством ${\text{diam}}(B(t) \cdot P) \leqslant M\hat {R}$, где $\hat {R}$ – любая наперед заданная постоянная.

Теорема 2. Если

то

Доказательство. Так как ${\text{diam}}({{X}^{{(0)}}}) < 2{{R}_{0}}$ по условию 3), то по лемме 2 множество A₀ обладает чебышевским слоем толщины R₀, что эквивалентно тому, что множество X⁽⁰⁾ является слабо выпуклым по Виалю с постоянной R₀ (см. [2, теорема 1.7.4]). Кроме того, в силу [2, лемма 1.3.4] множество X⁽⁰⁾ является замкнутым. Но тогда, по [2, теорема 1.8.1], множество X(T) является замкнутым, слабо выпуклым по Виалю множеством с постоянной $\hat {R}$. По [2, теорема 1.3.4] множество $X(T)$ является слабо выпуклым по Ефимову–Стечкину с той же константой $\hat {R}$, а из [2, теорема 1.4.1] следует его связность.

В силу леммы 3 имеем оценку

В свою очередь, применяя к множеству $X(T)$ теорему 1, получаем оценку (13).

3. ПРИМЕРЫ

ЗАКЛЮЧЕНИЕ

В настоящей работе получена оценка роста меры невыпуклости α множества достижимости для определенного класса управляемых систем, линейных по управлению. Это фактически первая оценка подобного рода и довольно грубая. В качестве возможных направлений дальнейших исследований наметим построение более тонких оценок для управляемых систем в фазовых пространствах большей размерности и прогнозирование меры невыпуклости α множеств достижимости для более широких классов управляемых систем.