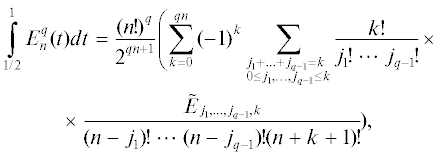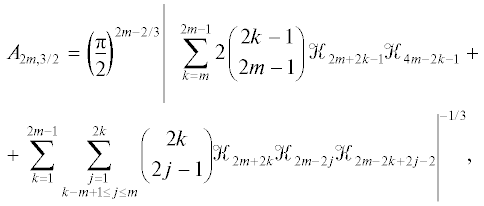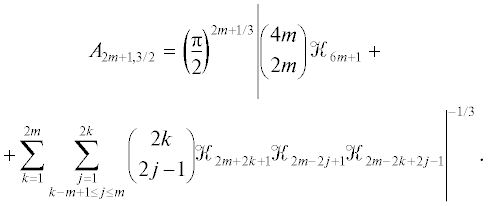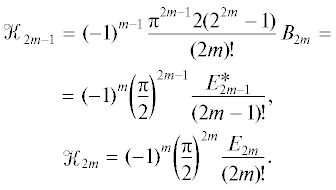1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 495, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 495, № 1, стр. 34-37

ОБ ОДНОЙ ЗАДАЧЕ ЭКСТРЕМАЛЬНОЙ ФУНКЦИОНАЛЬНОЙ ИНТЕРПОЛЯЦИИ И КОНСТАНТАХ ФАВАРА

Ю. С. Волков 1, *

1 Институт математики им. С.Л. Соболева Сибирского отделения Российской академии наук
Новосибирск, Россия

* E-mail: volkov@math.nsc.ru

Поступила в редакцию 01.06.2020
После доработки 01.10.2020
Принята к публикации 05.10.2020

Полный текст (PDF)

Аннотация

В задаче экстремальной функциональной интерполяции, впервые рассмотренной Ю.Н. Субботиным, вычислен явный вид констант экстремальной интерполяции через константы Фавара в пространствах Lp, p = 1, 3/2, 2. Найдены простые эффективные рекуррентные формулы для вычисления констант Фавара, также приведены формулы вычисления этих констант через числа Эйлера.

Ключевые слова: интерполяция, константы Фавара, рекуррентные формулы, числа Эйлера, многочлены Эйлера

В работе [1] авторы приводят обзор результатов по исследованию задач экстремальной функциональной интерполяции. Одна из задач состоит в следующем.

Пусть ${{Y}_{{n,p}}} = \{ y:y = {{{\text{\{ }}{{y}_{k}}{\text{\} }}}_{{k \in \mathbb{Z}}}},{\text{||}}{{\Delta }^{n}}y{\text{|}}{{{\text{|}}}_{{{{l}_{p}}}}} \leqslant 1\} $ – класс интерполируемых последовательностей y = ${{{\text{\{ }}{{y}_{k}}{\text{\} }}}_{{k \in \mathbb{Z}}}}$, удовлетворяющих условиям

$\begin{gathered} \sum\limits_{k \in \mathbb{Z}} {{{{\left| {{{\Delta }^{n}}{{y}_{k}}} \right|}}^{p}}} \leqslant 1,\quad 1 \leqslant p < \infty ; \\ \mathop {sup}\limits_{k \in \mathbb{Z}} \left| {{{\Delta }^{n}}{{y}_{k}}} \right| \leqslant 1,\quad p = \infty , \\ \end{gathered} $
${{\Delta }^{n}}y$ – последовательность, членами которой являются значения оператора обычной конечной разности порядка $n$ на последовательности $y$, т.е. значения
${{\Delta }^{n}}{{y}_{k}} = \sum\limits_{m = 0}^n {{{{( - 1)}}^{{n - m}}}} \left( {\begin{array}{*{20}{c}} n \\ m \end{array}} \right){{y}_{{k + m}}},\quad k \in \mathbb{Z},$
AC – множество всех локально абсолютно непрерывных функций. Класс функций, интерполирующих последовательность y в целочисленных точках числовой прямой, обозначим

$\begin{gathered} {{\Phi }_{{n,p}}}(y) = {\text{\{ }}f{\text{:}}\;{{f}^{{(n - 1)}}} \in AC, \\ {{f}^{{(n)}}} \in {{L}_{p}}(\mathbb{R}),\;f(k) = {{y}_{k}}\;\forall k \in \mathbb{Z}{\text{\} }} \\ \end{gathered} $

Задача экстремальной функциональной интерполяции состоит в нахождении константы экстремальной функциональной интерполяции

${{A}_{{n,p}}} = \mathop {sup}\limits_{y \in {{Y}_{{n,p}}}} \mathop {inf}\limits_{f \in {{\Phi }_{{n,p}}}(y)} {{\left\| {{{f}^{{(n)}}}} \right\|}_{{{{L}_{p}}}}}.$

В 1965 г. эта задача была решена Ю.Н. Субботиным [2] для $p = \infty $, точное значение было представлено в виде

${{A}_{{n,\infty }}} = \frac{1}{2}\mathop {\left( {\frac{\pi }{2}} \right)}\nolimits^{n + 1} \mathop {\left[ {\sum\limits_{\nu = 0}^\infty {\frac{{{{{( - 1)}}^{{\nu (n + 1)}}}}}{{{{{(2\nu + 1)}}^{{n + 1}}}}}} } \right]}\nolimits^{ - 1} .$

Это значение можно записать в терминах констант Фавара [3], а именно

(2)
${{A}_{{n,\infty }}} = \mathop {\left( {\frac{\pi }{2}} \right)}\nolimits_{}^n \mathcal{K}_{n}^{{ - 1}}.$

Экстремальной функцией, реализующей нижнюю грань в (1), был идеальный сплайн Эйлера (см. [3]).

В 1967 г. также Ю.Н. Субботин [4] получил решение для оставшихся случаев $1 \leqslant p < \infty $. Однако константа An,p была выражена через норму некоторого многочлена, а именно

(3)
${{A}_{{n,p}}} = (n - 1)!\left\| {{{Q}_{{n - 1}}}} \right\|_{{{{L}_{q}}[0,1]}}^{{ - 1}},$
где $\frac{1}{p} + \frac{1}{q} = 1$, а многочлен ${{Q}_{{n - 1}}}(x)$ выражен через многочлены Бернулли

${{Q}_{{n - 1}}}(x) = \frac{{{{2}^{{2n - 1}}}}}{n}\left[ {{{{( - 1)}}^{n}}{{B}_{n}}\left( {\frac{{1 - x}}{4}} \right) - {{B}_{n}}\left( {\frac{{1 + x}}{4}} \right)} \right].$

Отметим, что при $p = \infty $ в [4] нужная константа вычислялась через L1-норму этого же многочлена ${{Q}_{{n - 1}}}(x)$, поэтому можно говорить, что при всех $1 \leqslant p \leqslant \infty $ для вычисления константы An,p справедлива формула (3).

В обзоре [1] говорится, что вместо вычисления нормы многочлена ${{Q}_{{n - 1}}}(x)$ при $p < \infty $ найдена только асимптотика констант An,p при $n \to \infty $.

На самом деле для некоторых значений p норму многочлена ${{Q}_{{n - 1}}}(x)$ можно вычислить. Мы показываем, что норма многочлена выражается через числа Эйлера при любых целых q и приведем выражения констант An,p через константы Фавара при $p = 1,\;3{\text{/}}2,\;2$ (соответственно $q = \infty ,\;3,\;2$). Кроме того, мы приводим простые рекуррентные формулы для вычисления констант Фавара, а также формулы через числа Эйлера.

1. ВЫЧИСЛЕНИЕ КОНСТАНТ ЭКСТРЕМАЛЬНОЙ ФУНКЦИОНАЛЬНОЙ ИНТЕРПОЛЯЦИИ

Заметим, что многочлен ${{Q}_{{n - 1}}}(x)$ выражается через многочлен Эйлера. Действительно, воспользуемся последовательно свойствами многочленов Бернулли и Эйлера [5, 24.4.3] и [5, 24.4.23] (см. также [6, 1.12, 1.14]), тогда

$\begin{gathered} {{Q}_{{n - 1}}}(x) = \frac{{{{2}^{{2n - 1}}}}}{n}\left[ {{{B}_{n}}\left( {\frac{{x + 1}}{4} + \frac{1}{2}} \right)} \right. - \\ - \;\left. {{{B}_{n}}\left( {\frac{{1 + x}}{4}} \right)} \right] = {{2}^{{n - 1}}}{{E}_{{n - 1}}}\left( {\frac{{1 + x}}{2}} \right). \\ \end{gathered} $

При $0 \leqslant x \leqslant 1$ аргумент многочлена Эйлера будет принадлежать отрезку [1/2, 1], поэтому формулу (3) можно переписать в эквивалентном виде

${{A}_{{n,p}}} = \frac{{(n - 1)!}}{{{{2}^{{n - 1}}}{{2}^{{1/q}}}}}\left\| {{{E}_{{n - 1}}}} \right\|_{{{{L}_{q}}[1{\text{/}}2,\,1]}}^{{ - 1}}.$

Таким образом,

$\begin{gathered} \mathop {max}\limits_{0 \leqslant x \leqslant 1} \left| {{{Q}_{{n - 1}}}(x)} \right| = {{2}^{{n - 1}}}\mathop {max}\limits_{1/2 \leqslant x \leqslant 1} \left| {{{E}_{{n - 1}}}(x)} \right| = \\ = \;(n - 1)\,!\mathop {\,\left( {\frac{2}{\pi }} \right)}\nolimits_{}^{n - 1} {{\mathcal{K}}_{{n - 1}}}. \\ \end{gathered} $

Тогда в соответствии с (3) для p = 1 получаем

(4)
${{A}_{{n,1}}} = \mathop {\left( {\frac{\pi }{2}} \right)}\nolimits_{}^{n - 1} \mathcal{K}_{{n - 1}}^{{ - 1}}.$

Явное значение константы An,p можно получить и при p = 2, если заметить, что при $n + m$ четном справедливо равенство

$\int\limits_{1/2}^1 {{{E}_{n}}} (t){{E}_{m}}(t)dt = - \frac{n}{{m + 1}}\int\limits_{1/2}^1 {{{E}_{{n - 1}}}} (t){{E}_{{m + 1}}}(t)dt.$

Это свойство позволяет свести вычисление L2-нормы многочлена ${{E}_{{n - 1}}}(x)$ к вычислению L1-нормы многочлена ${{E}_{{2n - 2}}}(x)$, т.е. справедлива формула

$\int\limits_{1/2}^1 {E_{{n - 1}}^{2}} (t)dt = {{( - 1)}^{{n - 1}}}\frac{{{{{((n - 1)!)}}^{2}}}}{{(2n - 2)!}}\int\limits_{1/2}^1 {{{E}_{{2n - 2}}}} (t)dt.$

Следовательно

$\begin{gathered} \left\| {{{Q}_{{n - 1}}}} \right\|_{{{{L}_{2}}[0,1]}}^{2} = {{2}^{{2n - 1}}}\frac{{{{{((n - 1)!)}}^{2}}}}{{(2n - 2)!}}{{\left\| {{{E}_{{2n - 2}}}} \right\|}_{{{{L}_{1}}[1/2,1]}}} = \\ = \;{{((n - 1)!)}^{2}}\mathop {\left( {\frac{2}{\pi }} \right)}\nolimits_{}^{2n - 1} {{\mathcal{K}}_{{2n - 1}}}. \\ \end{gathered} $

В итоге получаем

${{A}_{{n,2}}} = \mathop {\left( {\frac{\pi }{2}} \right)}\nolimits_{}^{n - 1/2} \mathcal{K}_{{2n - 1}}^{{ - 1/2}}.$

Значения констант An,p можно также выразить через числа Эйлера или константы Фавара для тех значений p, при которых q будет целым. Для этого необходимо вычислить интеграл от соответствующей степени многочлена Эйлера на отрезке [1/2, 1]. Формулы для вычисления определенных интегралов от произведения многочленов Эйлера можно найти в работе [7]. Применительно к нашему случаю значения нужных интегралов выражаются в терминах обычных и смещенных чисел Эйлера.

Теорема 1 [7]. Для целого $q \geqslant 1$ справедливо равенство

где
$\begin{gathered} \mathop {\tilde {E}}\nolimits_{{{j}_{1}}, \ldots ,{{j}_{{q - 1}}},k} = {{( - 1)}^{{qn + 1}}}E_{{n - {{j}_{1}}}}^{ * }\; \cdots \;E_{{n - {{j}_{{q - 1}}}}}^{ * }E_{{n + k + 1}}^{ * } - \\ - \;{{E}_{{n - {{j}_{1}}}}}\; \cdots \;{{E}_{{n - {{j}_{{q - 1}}}}}}{{E}_{{n + k + 1}}}, \\ \end{gathered} $
${{E}_{i}} = {{2}^{i}}{{E}_{i}}(1{\text{/}}2)$ – числа Эйлера, $E_{i}^{ * } = {{2}^{i}}{{E}_{i}}(0)$ – смещенные числа Эйлера, причем при отрицательных индексах и одни, и другие числа Эйлера считаются нулевыми.

Заметим, что в выражении для $\mathop {\tilde {E}}\nolimits_{{{j}_{1}}, \ldots ,{{j}_{{q - 1}}},k} $ хотя бы одно из 2qn чисел Эйлера равно нулю, а если у них индексы разной четности, то и вся величина нулевая. Чтобы записать выражение для Lq-нормы многочлена Эйлера через константы Фавара, нужно оставить только ненулевые слагаемые. Для произвольного q это сделать тяжело, мы ограничимся случаем q = 3. Рассмотрим отдельно случаи четной и нечетной степени многочлена. Тогда эти выражения будут иметь вид

2. ВЫЧИСЛЕНИЕ КОНСТАНТ ФАВАРА

Мы показали, что в рассмотренных случаях константы экстремальной функциональной интерполяции An,p выражаются через константы Фавара, которые обычно определяют по формуле

${{\mathcal{K}}_{n}} = \frac{4}{\pi }\sum\limits_{\nu = 0}^\infty {\frac{{{{{( - 1)}}^{{\nu (n + 1)}}}}}{{{{{(2\nu + 1)}}^{{n + 1}}}}}} ,\quad n = 0,\;1,\; \ldots $

В теории приближения при решении экстремальных задач, получении оценок погрешности приближения и ряда других задач итоговые результаты часто принято выражать через константы Фавара (см. [3, 8, 9]). Однако в литературе мало освещено, как вычислять эти константы, хотя известна их связь с числами Бернулли и Эйлера

Числа Бернулли и Эйлера значительно лучше изучены, чем константы Фавара, и существует много эффективных способов их вычисления, а следовательно, и вычисления констант Фавара. Таким образом, вычисление через числа Бернулли и Эйлера – это один из способов вычисления констант Фавара.

Однако представляют несомненный интерес рекуррентные формулы, позволяющие вычислять константы Фавара сразу без привлечения каких-либо специальных чисел. Нам известны две рекуррентные формулы, полученные в работе [10], одна для вычисления четных констант Фавара, другая для нечетных. Мы предлагаем общие формулы, которые содержат в себе формулы работы [10].

Теорема 2. Справедливы равенства

(5)
$\begin{gathered} {{\mathcal{K}}_{0}} = 1,\quad {{\mathcal{K}}_{n}} = \left| {\sum\limits_{k = 0}^{\left[ {\frac{{n - 1}}{2}} \right]} {\frac{{{{{( - 1)}}^{k}}}}{{(n - 2k)!}}} \mathop {\left( {\frac{\pi }{2}} \right)}\nolimits_{}^{n - 2k} {{\mathcal{K}}_{{2k}}}} \right|, \\ n = 1,2, \ldots , \\ \end{gathered} $
(6)
$\begin{gathered} {{\mathcal{K}}_{0}} = 1, \\ {{\mathcal{K}}_{n}} = \left| {\frac{1}{{n!}}{{{\left( {\frac{\pi }{2}} \right)}}^{n}} + \sum\limits_{k = 1}^{\left[ {\frac{n}{2}} \right]} {\frac{{{{{( - 1)}}^{k}}}}{{(n - 2k + 1)!}}} {{{\left( {\frac{\pi }{2}} \right)}}^{{n - 2k + 1}}}{{\mathcal{K}}_{{2k - 1}}}} \right|, \\ n = 1,2,... \\ \end{gathered} $

Заметим, что обе формулы в теореме 2 можно объединить в одну.

Следствие 1. Справедливы равенства

$\begin{gathered} {{\mathcal{K}}_{0}} = 1, \\ {{\mathcal{K}}_{n}} = \frac{1}{2}\left| {\frac{1}{{n!}}\mathop {\left( {\frac{\pi }{2}} \right)}\nolimits^n - \sum\limits_{k = 0}^{n - 1} {\frac{{{{{( - 1)}}^{{n(k + 1) + \left[ {\frac{k}{2}} \right]}}}}}{{(n - k)!}}} \mathop {\left( {\frac{\pi }{2}} \right)}\nolimits_{}^{n - k} {{\mathcal{K}}_{k}}} \right|, \\ n = 1,\;2,\; \ldots \\ \end{gathered} $

Формулы (5), (6) не очень сложны и после некоторых вычислений дают явные значения нужных констант (можно написать программу для компьютера). Однако оказывается, можно получить совсем простые рекуррентные формулы.

Теорема 3. Справедливы равенства

(7)
$\begin{gathered} {{\mathcal{K}}_{0}} = 1,\quad {{\mathcal{K}}_{1}} = \frac{\pi }{2}, \\ {{\mathcal{K}}_{n}} = \frac{\pi }{{2n}}\sum\limits_{k = 1}^{\left[ {\tfrac{n}{2}} \right]} {{{\mathcal{K}}_{{2k - 1}}}} {{\mathcal{K}}_{{n - 2k}}},\quad n = 2,\;3,\; \ldots , \\ \end{gathered} $
(8)
$\begin{gathered} {{\mathcal{K}}_{0}} = 1, \\ {{\mathcal{K}}_{n}} = \frac{\pi }{{2n}}\sum\limits_{k = 0}^{\left[ {\frac{{n - 1}}{2}} \right]} {{{\mathcal{K}}_{{2k}}}{{\mathcal{K}}_{{n - 1 - 2k}}},\quad n = 1,2,...} \\ \end{gathered} $

Обратим внимание, что если n четное, то формулы (7) и (8) совпадают. А для нечетных они разные, но их также можно объединить в одну.

Следствие 2. Справедливы равенства

$\begin{gathered} {{\mathcal{K}}_{0}} = 1,\quad {{\mathcal{K}}_{1}} = \frac{\pi }{2}, \\ {{\mathcal{K}}_{n}} = \frac{\pi }{{4n}}\sum\limits_{k = 0}^{n - 1} {{{\mathcal{K}}_{k}}} {{\mathcal{K}}_{{n - 1 - k}}},\quad n = 2,\;3,\; \ldots \\ \end{gathered} $

Как отмечает Ю.Н. Субботин [4, с. 32] константы экстремальной функциональной интерполяции An,p должны быть монотонны по параметру p, поэтому, как следствие вычисленных значений констант, мы получаем неравенства, связывающие соседние константы Фавара.

Теорема 4. Для любого $n \geqslant 1$ справедливы неравенства

$\frac{2}{\pi }\mathcal{K}_{n}^{2} \leqslant {{\mathcal{K}}_{{2n - 1}}} \leqslant \frac{\pi }{2}\mathcal{K}_{{n - 1}}^{2}.$

Список литературы

  1. Субботин Ю.Н., Новиков С.И., Шевалдин В.Т. // Тр. ИММ УрО РАН. 2018. Т. 24. № 3. С. 200–225.

  2. Субботин Ю.Н. // Тр. МИАН СССР. 1965. Т. 78. С. 24–42.

  3. Корнейчук Н.П. // Точные константы в теории приближения. М.: Наука, 1987.

  4. Субботин Ю.Н. // Тр. МИАН СССР. 1967. Т. 88. С. 30–60.

  5. Dilcher K. NIST handbook of mathematical functions. Washington: U.S. Dept. Commerce, 2010. https://dlmf.nist.gov/24

  6. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра. М.: Наука, 1965.

  7. Liu J., Pan H., Zhang Y. // Integral Transforms Spec. Funct. 2014. V. 25. № 9. P. 680–685.

  8. Тихомиров В.М. // Некоторые вопросы теории приближений. М.: МГУ, 1976.

  9. Волков Ю.С., Субботин Ю.Н. // Тр. ИММ УрО РАН. 2014. Т. 20. № 1. С. 52–67.

  10. Gocheva-Ilieva S.G., Feschiev I.H. // Abstr. Appl. Anal. 2013. 523618.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал