Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 497, № 1, стр. 35-37

1. ПОСТАНОВКА ЗАДАЧИ

Для решения поставленной задачи уточним используемые понятия. Как известно, модель гармонического, синусоидального сигнала с постоянной амплитудой эффективно используется в теории. На практике же неизбежное воздействие шума на процесс распространения любого исходно гармонического сигнала приводит к случайным флуктуациям величин амплитуды и фазы такого сигнала. В результате образуется так называемый квазигармонический сигнал, амплитуда и фаза которого представляют собой случайные величины. В каждый момент времени t такой сигнал может быть представлен в следующей форме:

где ω – частота, R(t) – амплитуда, или огибающая сигнала, которая изменяется случайным образом под воздействием гауссовского шума, величина фазы φ(t) также изменяется во времени случайным образом под воздействием шума в силу амплитудно-фазовой модуляции. Рассмотрим сигнал (1) в комплексной плоскости, как комплексную величину, обозначив ее S(t):

Для изучения фазовых характеристик сигналов мы будем анализировать “медленную” составляющую сигнала, т.е. функцию s(t) = R(t)exp[iφ(t)]. Обозначим “медленную” составляющую исходного гармонического, не искаженного шумом комплексного сигнала как вектор A(A, φ₀), характеризуемый постоянными величинами амплитуды A и фазы φ₀. Распространение сигнала по какой-либо среде неизбежно сопровождается тем, что действительная Acosφ₀ и мнимая Asinφ₀ составляющие исходного сигнала независимо изменяются под воздействием большого числа случайных шумовых составляющих. Обозначим как r(r, ψ) суммарный вектор шума, который накладывается на исходный сигнал A, искажая его. Компоненты r_x, r_y вектора шума r являются независимыми случайными величинами и подчиняются нормальному распределению: ${{\bar {r}}_{x}} = {{\bar {r}}_{y}} = 0$, $\overline {r_{x}^{2}} = \overline {r_{y}^{2}} $ = = σ², где величина σ² представляет собой дисперсию шума. Очевидно, что амплитуда r шумового вектора и его фаза ψ представляют собой независимые случайные величины и распределены следующим образом: случайная величина амплитуды r подчиняется статистическому распределению Рэлея, в то время как фаза ψ шумовой компоненты распределена равномерно на интервале (0, 2π).

2. РАСЧЕТ ФУНКЦИИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ФАЗЫ КВАЗИГАРМОНИЧЕСКОГО СИГНАЛА

Обозначим как вектор R(R, φ) “медленную” составляющую результирующего квазигармонического сигнала, формируемого суммированием исходного гармонического сигнала A и шума r: R = A + r. Нетрудно показать, что совместная функция распределения случайных величин амплитуды R и фазы φ результирующего сигнала R определяется выражением [6]

Из (3) следует, что распределения амплитуды R и фазы φ результирующего сигнала не являются независимыми, причем фаза φ результирующего сигнала, в отличие от фазы ψ шумовой составляющей, уже не является равномерно распределенной величиной.

Для определения функции плотности вероятности статистического распределения фазы квазигармонического сигнала проинтегрируем выражение (3) по $R$ в пределах от нуля до бесконечности. В результате вычислений получаем

где используются следующие обозначения: η = = $\frac{A}{{\sqrt 2 \sigma }}\cos (\varphi - {{\varphi }_{0}})$, а функция Φ(η) представляет собой известную специальную функцию, называемую интегралом ошибок: $\Phi \left( \eta \right) = \frac{2}{{\sqrt \pi }}\int\limits_0^\eta {{{e}^{{ - {{t}^{2}}}}}dt} $.

Формула (4) характеризует распределение фазы случайного сигнала, полученного в результате воздействия гауссовского шума с дисперсией σ² на исходно детерминированный сигнал A с амплитудой A и фазой φ₀. Нетрудно видеть, что в предельном случае отсутствия детерминированной составляющей, т.е. при A = 0, ожидаемо получаем равномерное распределение фазы сигнала: ${{\omega }_{\varphi }}(\varphi )d\varphi \left| {_{{A = 0}}} \right. = \frac{1}{{2\pi }}d\varphi $.

Введем обозначение $S = \frac{A}{{\sqrt 2 \sigma }}$. Величину S ² = $\frac{{{{A}^{2}}}}{{2{{\sigma }^{2}}}}$ часто используют в качестве характеристики отношения сигнала к шуму. С учетом введенного параметра $S$ выражение для выше введенного параметра $\eta $ имеет вид $\eta = S\cos \left( {\varphi - {{\varphi }_{0}}} \right)$.

Из вышеизложенного следует, что статистическое распределение фазы, описываемое выражением (4), определяется двумя параметрами задачи: отношением сигнала к шуму $S$ и величиной отклонения текущего значения фазы $\varphi $ от значения фазы ${{\varphi }_{0}}$ исходного сигнала, и является четной функцией этого отклонения, что вполне ожидаемо. Для функции плотности вероятности распределения фазы будем использовать обозначение ${{\omega }_{\varphi }}\left( {\varphi \left| {S,{{\varphi }_{0}}} \right.} \right)$:

На рис. 1 представлены графики функции плотности вероятности распределения фазы квазигармонического сигнала в зависимости от значения параметра отношения сигнала к шуму S (рис. 1а), а также трехмерный график этой функции (рис. 1б). На рис. 1б по оси $x$ отложена величина фазы, вдоль оси $y$ отложена величина отношения сигнала к шуму.

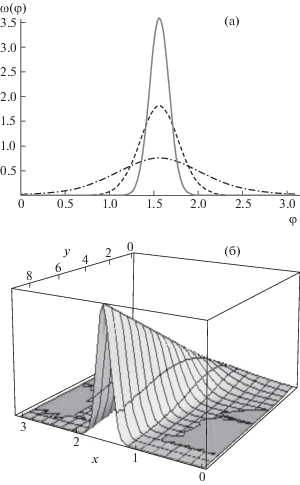
Как следует из представленных графических данных, с ростом величины отношения сигнала к шуму функция плотности вероятности фазы сигнала заметно сужается, что вполне ожидаемо, учитывая, что в предельном случае очень малой величины отношения сигнала к шуму мы имеем сигнал, состоящий практически из шумовой составляющей, с функцией плотности вероятности, близкой к равномерной, в то время как при большой величине отношения сигнала к шуму мы имеем практически детерминированный сигнал, функция плотности вероятности которого близка к $\delta $-функции.

ЗАКЛЮЧЕНИЕ

В работе теоретически исследуется статистическое распределение величины фазы квазигармонического сигнала, впервые получено аналитическое выражение для функции плотности вероятности распределения фазы. Показано, что данное распределение является двухпараметрическим и определяется следующими параметрами: величиной отношения сигнала к шуму и величиной отклонения фазы от ее значения, соответствующего исходно детерминированному, незашумленному сигналу.

Полученные в работе результаты вносят вклад в развитие теории вероятностей и могут эффективно использоваться при решении различных научных и прикладных задач, связанных с высокоточными измерениями фазы квазигармонического сигнала, в частности, в таких областях науки и техники, как радиофизика, оптика, радиолокация, радионавигация, метрология.