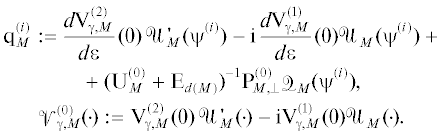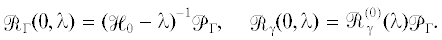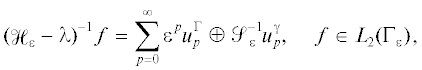Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 498, № 1, стр. 21-26

1. ПОСТАНОВКА ЗАДАЧИ

Теория квантовых графов, а именно, теория эллиптических операторов на метрических графах, достаточно активно развивается, и одним из направлений является теория возмущений для таких операторов. Графы допускают специфическое возмущение геометрического характера – наличие малых ребер. Влияние таких ребер на резольвенты и спектры рассматриваемых эллиптических операторов исследовалось ранее с точки зрения установления сходимости резольвенты к резольвенте некоторого предельного оператора на предельном графе или множестве, см., например, [1–3]. Общие результаты о резольвентной сходимости операторов Шрёдингера на графах с малыми ребрами были недавно опубликованы в статье [1]. Эта статья мотивировала настоящую работу, и нашей целью являются рассмотрение общих эллиптических скалярных операторов второго порядка на графах с малыми ребрами и детальное изучение зависимости их резольвент от длин малых ребер. Частные результаты такого характера для простейших модельных графов были получены в [5, 6].

Опишем постановку задачи. Пусть $\Gamma $ – метрический граф с конечным числом ребер и вершин, не имеющий изолированных вершин. Ребра могут иметь конечную или бесконечную длину. Выберем произвольно вершину ${{M}_{0}} \in \Gamma $ и через ${\text{e}}_{i}^{0}$, $i = 1, \ldots ,{{d}_{0}}$, обозначим ребра, выходящие из ${{M}_{0}}$, причем петли пересчитываются дважды. Через $\gamma $ обозначим еще один метрический конечный граф с ребрами конечной длины, а через ${{\gamma }_{\varepsilon }}$ – граф, полученный из $\gamma $ сжатием каждого из ребер в ${{\varepsilon }^{{ - 1}}}$ раз с сохранением структуры и вершин графа, где $\varepsilon $ – малый положительный параметр. Выберем произвольный набор вершин M_j, $j = 1, \ldots ,n$, в графе ${{\gamma }_{\varepsilon }}$, где $n \leqslant {{d}_{0}}$, и произвольно разобьем ребра ${\text{e}}_{i}^{0}$, $i = 1, \ldots ,{{d}_{0}}$, на n непустых групп ${{\{ {\text{e}}_{i}^{0}\} }_{{i \in {{J}_{j}}}}}$, $j = 1, \ldots ,n$, ${{J}_{j}}$ – соответствующие множества индексов. Вершину ${{M}_{0}}$ заменим на n ее копий, по одной для каждой из групп ${{\{ {\text{e}}_{i}^{0}\} }_{{i \in {{J}_{j}}}}}$, и каждую копию отождествим с вершиной ${{M}_{j}}$ в графе ${{\gamma }_{\varepsilon }}$. В результате получим новый граф, обозначаемый символом ${{\Gamma }_{\varepsilon }}$, который возник в результате описанного приклеивания графа ${{\gamma }_{\varepsilon }}$ с малыми ребрами к исходному графу $\Gamma $. На каждом из ребер всех рассматриваемых графов произвольно выберем направление и соответствующую ему переменную. Далее мы отождествляем исходные графы $\Gamma $ и ${{\gamma }_{\varepsilon }}$ с соответствующими подграфами в графе ${{\Gamma }_{\varepsilon }}$.

Настоящая работа посвящена исследованию оператора ${{\mathcal{H}}_{\varepsilon }}$ в ${{L}_{2}}({{\Gamma }_{\varepsilon }})$ с дифференциальным выражением

где $V_{\Gamma }^{{(i)}} \in W_{\infty }^{1}(\Gamma )$, $V_{\gamma }^{{(i)}} \in W_{\infty }^{1}(\gamma )$, i = 1, 2, $V_{\Gamma }^{{(0)}} \in {{L}_{2}}(\Gamma )$, $V_{\gamma }^{{(1)}} \in {{L}_{2}}(\gamma )$ – вещественные функции, голоморфные по ε в норме указанных пространств, ${{\mathcal{S}}_{\varepsilon }}{\kern 1pt} :\;{{L}_{2}}(\gamma ) \to {{L}_{2}}({{\gamma }_{\varepsilon }})$ – линейный оператор, действующий по правилу $({{\mathcal{S}}_{\varepsilon }}u)(x): = u\left( {\tfrac{x}{\varepsilon }} \right)$, $x \in {{{\text{e}}}_{\varepsilon }}$ на каждом ребре ${{{\text{e}}}_{\varepsilon }} \in {{\gamma }_{\varepsilon }}$, и выполнено условие эллиптичности: $V_{\varepsilon }^{{(2)}}(x,\varepsilon ) \geqslant {{c}_{\mathcal{H}}} > 0$ на Γ_ε, где ${{c}_{\mathcal{H}}}$ – константа, не зависящая от x и ε.

Краевые условия в произвольной вершине $M \in {{\Gamma }_{\varepsilon }}$, из которой выходят ребра ${{{\text{e}}}_{i}}(M)$, i = 1, ..., $d(M)$, задаем следующим образом. Пусть u_i := $u{{{\text{|}}}_{{{{{\text{e}}}_{i}}(M)}}}$, $i = 1, \ldots ,d(M)$ – сужения заданной на ${{\Gamma }_{\varepsilon }}$ функции u на ребра ${{{\text{e}}}_{i}}(M)$ и

где ${{x}_{i}}$ – переменная на ребре ${\text{e}}_{i}^{{}}(M)$. В вершине M затем задается краевое условие общего вида где ${{{\text{A}}}_{M}}(\varepsilon )$ и ${{{\text{B}}}_{M}}(\varepsilon )$ – заданные матрицы размера $d(M) \times d(M)$, голоморфные по ε. Предполагается, что матрица самосопряжена, где обозначено ${{\nu }_{i}}(M): = 1$, если направление от вершины M на ребре ${{{\text{e}}}_{i}}(M)$ совпадает с выбранным направлением на этом ребре и ${{\nu }_{i}}(M): = - 1$ иначе.

Матрицы ${{{\text{A}}}_{M}}(\varepsilon )$ и ${{{\text{B}}}_{M}}(\varepsilon )$ в (3) определены с точностью до умножения слева на произвольную невырожденную квадратную матрицу размера $d(M)$ × × d(M). Поэтому, обозначив r(M) := ${\text{rank}}{{{\text{B}}}_{M}}(0)$, далее предполагаем, что первые $r(M)$ строк матрицы ${{{\text{B}}}_{M}}(0)$ линейно независимы, а остальные строки обращаются в нуль, а каждая из последних $d(M)$ – ‒ r(M) строк матрицы ${{{\text{A}}}_{M}}(0)$ не равна нулю. Также налагаем следующее условие: ${\text{rank}}({{{\text{A}}}_{M}}(0){{{\text{B}}}_{M}}(0))$ = = d(M).

Область определения оператора ${{\mathcal{H}}_{\varepsilon }}$ состоит из функций из $\dot {W}_{2}^{2}({{\gamma }_{\varepsilon }})$, удовлетворяющих краевым условиям (3), где обозначено $\dot {W}_{2}^{j}( \cdot ): = \mathop \oplus \limits_{{\text{e}} \in \cdot } \,W_{2}^{j}({\text{e}})$, $j = 1,2$. Действие оператора на таких функциях определяется дифференциальным выражением (1). Описанные условия на функции $V_{\Gamma }^{{(i)}}$, $V_{\gamma }^{{(i)}}$ и матрицы ${{{\text{A}}}_{M}}$, ${{{\text{B}}}_{M}}$ являются критерием самосопряженности оператора .

2. ВСПОМОГАТЕЛЬНЫЕ ОБОЗНАЧЕНИЯ

Через ${{\gamma }_{\infty }}$ обозначим граф, полученный приклеиванием полубесконечных ребер ${\text{e}}_{i}^{\infty }$, $i \in {{J}_{j}}$, $j = 1, \ldots ,n$, к вершинам M_j, $j = 1, \ldots ,n$, графа γ, считая данные вершины началами ребер ${\text{e}}_{i}^{\infty }$. Переменную на графе ${{\gamma }_{\infty }}$ обозначим через $\xi $ и рассмотрим на нем оператор 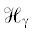с дифференциальным выражением:

и краевыми условиями в вершинах $M \in {{\gamma }_{\infty }}$: где векторы ${{\mathcal{U}}_{M}}(u)$ и $\mathcal{U}_{M}^{'}(u)$ вводятся также, как и в (2) с заменой производных $\tfrac{{d{{u}_{i}}}}{{d{{x}_{i}}}}$ на $\tfrac{{d{{u}_{i}}}}{{d{{\xi }_{i}}}}$, а матрицы имеют вид

Здесь ${\text{A}}_{M}^{ + }$ и ${\text{B}}_{M}^{ + }$ – матрицы, состоящие из первых $r(M)$ строк матриц ${{{\text{A}}}_{M}}$ и ${{{\text{B}}}_{M}}$, соответственно, а матрицы ${\text{A}}_{M}^{ - }$ и ${\text{B}}_{M}^{ - }$ образованы оставшимися $d(M)$ – ‒ r(M) строками матриц ${{{\text{A}}}_{M}}$ и ${{{\text{B}}}_{M}}$. Область определения оператора состоит из функций из $\dot {W}_{2}^{2}(\gamma )$, удовлетворяющих краевым условиям (5). Оператор самосопряжен. С учетом структуры графа ${{\gamma }_{\infty }}$ и вида дифференциального выражения $\mathop {\hat {\mathcal{H}}}\nolimits_\gamma $ на ребрах ${\text{e}}_{i}^{\infty }$, существенный спектр оператора совпадает с полупрямой $[0, + \infty )$.

Основное и по сути единственное условие, которое мы налагаем в работе, звучит следующим образом:

(A) край существенного спектра оператора 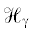не является собственным значением.

Данное условие эквивалентно тому, что задача для уравнения

с условиями (5) не имеет нетривиальных решений из $\dot {W}_{2}^{2}(\gamma ) \oplus \mathop \oplus \limits_{i = 1, \ldots ,{{d}_{0}}} \,W_{{2,loc}}^{2}({\text{e}}_{i}^{\infty })$, которые бы тождественно обращались в нуль на ребрах ${\text{e}}_{i}^{\infty }$. При этом задача (5), (6) может иметь нетривиальные решения из $\dot {W}_{2}^{2}(\gamma ) \oplus \mathop \oplus \limits_{i = 1, \ldots ,{{d}_{0}}} \,W_{{2,loc}}^{2}({\text{e}}_{i}^{\infty })$, которые постоянны на ребрах ${\text{e}}_{i}^{\infty }$. В терминах оператора это означает, что он может иметь виртуальный уровень на краю существенного спектра.

Пусть ${{\psi }^{{(j)}}}$, $j = 1, \ldots ,k$, – линейно независимые ограниченные нетривиальные решения задачи (5), (6), не равные тождественно нулю на ребрах ${\text{e}}_{i}^{\infty }$. Ясно, что в силу условия (A) выполнено неравенство $k \leqslant {{d}_{0}}$. Если таких решений нет, то полагаем $k = 0$.

Для произвольной функции u, заданной и непрерывной на ребрах ${\text{e}}_{i}^{\infty }$ в окрестности вершин ${{M}_{j}}$, обозначим

где $u{{{\text{|}}}_{{{\text{e}}_{i}^{\infty }}}}$ – сужение u на ребро ${\text{e}}_{i}^{\infty }$. В силу своего определения функции ${{\psi }^{{(j)}}}$ удовлетворяют условию ${{\Psi }^{{(j)}}}: = {{\mathcal{U}}_{\gamma }}({{\psi }^{{(j)}}}) \ne 0$, $j = 1, \ldots ,k$. Выберем функции ${{\psi }^{{(j)}}}$ так, чтобы вектора ${{\Psi }^{{(j)}}}$ были ортонормированы в ${{\mathbb{C}}^{{{{d}_{0}}}}}$. Если $k < {{d}_{0}}$, то дополнительно произвольно выберем векторы ${{\Psi }^{{(j)}}} \in {{\mathbb{C}}^{{{{d}_{0}}}}}$, $j = k + 1$, ..., d₀, так, что набор ${{\Psi }^{{(j)}}} \in {{\mathbb{C}}^{{{{d}_{0}}}}}$, $j = 1$, ..., d₀, образует ортонормированный базис в ${{\mathbb{C}}^{{{{d}_{0}}}}}$, а матрица Ψ := :=  $({{\Psi }^{{(1)}}} \ldots {{\Psi }^{{(k)}}}\,\,{{\Psi }^{{(k + 1)}}} \ldots {{\Psi }^{{({{d}_{0}})}}})$ унитарна.

Для каждой вершины $M \in {{\gamma }_{\infty }}$ определим матрицы:

где ${{{\text{e}}}_{i}}(M)$ – ребра, выходящие из вершины M, числа ${{\nu }_{i}}(M)$ определяются как и в (4), а функции $V_{\gamma }^{{(j)}}$ считаем продолженными на ребра ${\text{e}}_{i}^{\infty }$, $i \in {{J}_{j}}$, $j = 1$, ..., n, по формулам $V_{\gamma }^{{(2)}}( \cdot ,\varepsilon ) \equiv {\text{v}}_{i}^{{(2)}}(\varepsilon )$, $V_{\gamma }^{{(1)}}( \cdot ,\varepsilon ) \equiv \varepsilon {\text{v}}_{i}^{{(1)}}(\varepsilon )$.

Матрица ${\text{U}}_{M}^{{(0)}}$ унитарна. Через ${\text{P}}_{M}^{{(0)}}$ обозначим проектор в ${{\mathbb{C}}^{{d(M)}}}$ на собственное подпространство матрицы ${\text{U}}_{M}^{{(0)}}$, соответствующее собственному значению –1, и пусть ${\text{P}}_{{M, \bot }}^{{(0)}}: = {{{\text{E}}}_{{d(M)}}} - {\text{P}}_{M}^{{(0)}}$. Через Q обозначим самосопряженную матрицу размера k × k с элементами

Определим еще две блочные матрицы размера ${{d}_{0}} \times {{d}_{0}}$: где символом E_p обозначаем единичные матрицы размера p × p, символ 0 в первой строке матрицы ${{{\text{A}}}_{{{{M}_{0}}}}}$ обозначает матрицу размера $k \times ({{d}_{0}} - k)$, а во второй строке – матрицу размера $({{d}_{0}} - k) \times k$. Символами 0 в определении матрицы ${{{\text{B}}}_{{{{M}_{0}}}}}$ обозначаем нулевые матрицы соответственно размеров $k \times ({{d}_{0}} - k)$, $({{d}_{0}} - k) \times k$ и $({{d}_{0}} - k) \times ({{d}_{0}} - k)$. Матрицы ${\text{V}}_{{\Gamma ,{{M}_{0}}}}^{{(j)}}$, $j = 1,2$, задаются равенством где числа ${{\nu }_{i}}({{M}_{0}})$ вводятся согласно (4).

Пусть – оператор на графе $\Gamma $ с дифференциальным выражением

$V_{0}^{{(i)}}: = V_{\Gamma }^{{(i)}}( \cdot ,0)$, с краевыми условиями где матрицы ${\text{A}}_{{{{M}_{0}}}}^{{(0)}}$, ${\text{B}}_{{{{M}_{0}}}}^{{(0)}}$ заданы в (7), а для $M \ne {{M}_{0}}$ они вводятся формулами ${\text{A}}_{M}^{{(0)}}: = {{{\text{A}}}_{M}}(0)$, ${\text{B}}_{M}^{{(0)}}$ := B_M(0). Оператор действует в ${{L}_{2}}(\Gamma )$ на области определения, состоящей из функций из $\dot {W}_{2}^{2}(\Gamma )$, удовлетворяющих краевым условиям (8). Данный оператор самосопряжен.

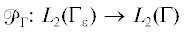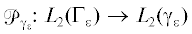Пусть и операторы сужения на подграфы $\Gamma $ и ${{\gamma }_{\varepsilon }}$ в $\Gamma $, действующие на каждую $f \in {{L}_{2}}({{\Gamma }_{\varepsilon }})$ по правилам , . В смысле прямой суммы ${{L}_{2}}({{\Gamma }_{\varepsilon }}) = {{L}_{2}}(\Gamma ) \oplus {{L}_{2}}({{\gamma }_{\varepsilon }})$ для этих операторов верно равенство

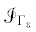где – тождественный оператор в ${{L}_{2}}({{\Gamma }_{\varepsilon }})$.

Так как оператор самосопряжен, то для каждого $\lambda \in \mathbb{C}{{\backslash }}\mathbb{R}$ его резольвента корректно определена, что позволяет определить еще пару операторов

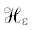линейных и ограниченных как действующих из ${{L}_{2}}(\Gamma ) \oplus {{L}_{2}}(\gamma )$ в $\dot {W}_{2}^{2}(\Gamma )$ и $\dot {W}_{2}^{2}(\gamma )$ соответственно. Здесь прямые суммы понимаются в смысле равенства (9), а исходная резольвента оператора легко восстанавливается с помощью введенных операторов по формуле

Определим еще один оператор : L₂(Γ) → → $\dot {W}_{2}^{2}(\gamma )$, действующий по правилу

где ${{\Psi }_{0}}: = ({{\Psi }^{{(1)}}} \ldots {{\Psi }^{{(k)}}})$. Введем следующие пространства непрерывных функций на графах: где считаем ${{\dot {C}}^{0}}: = \dot {C}$. Если функции $V_{\Gamma }^{{(i)}}$ и $V_{\gamma }^{{(i)}}$ имеют гладкость $V_{\Gamma }^{{(i)}} \in {{\dot {C}}^{1}}(\Gamma )$, $V_{\gamma }^{{(i)}} \in {{\dot {C}}^{1}}(\gamma )$, $i = 1,2$, $V_{\Gamma }^{{(0)}} \in \dot {C}(\Gamma )$, $V_{\gamma }^{{(0)}} \in \dot {C}(\gamma )$ и голоморфны по $\varepsilon $ в норме этих пространств, то тогда полагаем

3. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Сформулируем основные результаты работы.

Теорема 1. Пусть выполнены описанные выше условия на функции $V_{\Gamma }^{{(i)}}$, $V_{\gamma }^{{(i)}}$ и матрицы ${{{\text{A}}}_{M}}(\varepsilon )$, ${{{\text{B}}}_{M}}(\varepsilon )$ и выполнено условие (A). Тогда для любого $\lambda \in \mathbb{C}{{\backslash }}\mathbb{R}$ существует ${{\varepsilon }_{0}}(\lambda ) > 0$, такое что при $\varepsilon < {{\varepsilon }_{0}}(\lambda )$ операторы ${{\mathcal{R}}_{\Gamma }}(\varepsilon ,\lambda )$ и ${{\mathcal{R}}_{\gamma }}(\varepsilon ,\lambda )$ ограничены и голоморфны по $\varepsilon $ как действующие из ${{L}_{2}}(\Gamma ) \oplus {{L}_{2}}(\gamma )$ в $\dot {W}_{2}^{2}(\Gamma ) \cap {{\dot {C}}^{2}}(\Gamma )$ и $\dot {W}_{2}^{2}(\gamma ) \cap {{\dot {C}}^{2}}(\gamma )$. Первые члены рядов Тейлора этих операторов имеют вид

Поясним действие операторов ${{\mathcal{R}}_{\Gamma }}(\varepsilon ,\lambda )$ и ${{\mathcal{R}}_{\gamma }}(\varepsilon ,\lambda )$. Пусть $f \in {{L}_{2}}({{\Gamma }_{\varepsilon }})$, ${{u}_{\varepsilon }}: = {{({{\mathcal{H}}_{\varepsilon }} - \lambda )}^{{ - 1}}}f$ и рассмотрим сужения этих функций на подграфы Γ и ${{\gamma }_{\varepsilon }}$; сужения на ${{\gamma }_{\varepsilon }}$ дополнительно будем рассматривать как функции переменной $\xi : = x{{\varepsilon }^{{ - 1}}}$, $\xi \in \gamma $. Эти сужения очевидно имеют вид ${{\mathcal{R}}_{\Gamma }}f$, ${{\mathcal{P}}_{\Gamma }}{{u}_{\varepsilon }}$ и , . Операторы ${{\mathcal{R}}_{\Gamma }}(\varepsilon ,\lambda )$ и ${{\mathcal{R}}_{\gamma }}(\varepsilon ,\lambda )$ отображают пару соответственно в ${{\mathcal{P}}_{\Gamma }}{{u}_{\varepsilon }}$ и $\mathcal{S}_{\varepsilon }^{{ - 1}}{{\mathcal{P}}_{{{{\gamma }_{\varepsilon }}}}}{{u}_{\varepsilon }}$. С учетом формулы (10) их можно рассматривать как части резольвенты ${{({{\mathcal{H}}_{\varepsilon }} - \lambda )}^{{ - 1}}}$, соответствующие подграфам Γ и ${{\gamma }_{\varepsilon }}$. Теорема 1 утверждает голоморфность по ε этих частей, а формулы (11) дают первые члены их рядов Тей- лора.

Нам также удалось разработать эффективный рекуррентный алгоритм определения всех коэффициентов рядов Тейлора для операторов ${{\mathcal{R}}_{\Gamma }}(\varepsilon ,\lambda )$ и ${{\mathcal{R}}_{\gamma }}(\varepsilon ,\lambda )$. А именно, для произвольной пары функций $({{f}_{\Gamma }},{{f}_{\gamma }}) \in {{L}_{2}}(\Gamma ) \oplus {{L}_{2}}(\gamma )$ данные ряды Тейлора имеют вид

где функции $u_{p}^{\Gamma }$ и $u_{p}^{\gamma }$ являются решениями рекуррентной системы однозначно разрешимых краевых задач на Γ и γ соответственно. В этих задачах уравнения на $u_{p}^{\Gamma }$ и $u_{p}^{\gamma }$ описываются с помощью дифференциальных выражений ${{\hat {\mathcal{H}}}_{0}}$ и ${{\hat {\mathcal{H}}}_{\gamma }}$ соответственно. Правые части уравнений и краевые условия для функций $u_{p}^{\Gamma }$ зависят только от функций $u_{q}^{\Gamma }$, $q < p$, а аналогичные правые части для функций $u_{p}^{\gamma }$ – от функций $u_{q}^{\gamma }$, $q < p$. Краевые условия в вершине M₀ для функций $u_{p}^{\Gamma }$ определяются функциями $u_{p}^{\gamma }$, а краевые условия в вершинах M_j для функций $u_{p}^{\gamma }$ – функциями $u_{{p - 1}}^{\Gamma }$. Последовательно решая эти краевые задачи, можно найти все функции $u_{p}^{\Gamma }$ и $u_{p}^{\gamma }$.

Наша схема построения коэффициентов рядов Тейлора (12) по сути является адаптацией метода согласования асимптотических разложений [7] для графов. Наша работа первая, где этот метод применяется для исследования квантовых графов. Отдельно следует подчеркнуть, что наличие малых ребер в графе является сингулярным возмущением. Вместе с тем, в отличие от большинства задач с сингулярными возмущениями, см., например, модели в [7], получающиеся здесь асимптотические ряды для решения одновременно оказываются равномерно сходящимися по параметру рядами Тейлора, что весьма редкий случай в сингулярно возмущенных краевых задачах.

Наличие рядов Тейлора (12) и формула (10) позволяют найти представление для резольвенты ${{({{\mathcal{H}}_{\varepsilon }} - \lambda )}^{{ - 1}}}$ в виде равномерно сходящегося ряда, частичные суммы которого дают сколько угодно точные аппроксимации резольвенты. Данный результат сформулирован в следующей теореме.

Теорема 2. В предположениях теоремы 1, резольвента представляется равномерно сходящимся в $\dot {W}_{2}^{2}({{\Gamma }_{\varepsilon }})$ и ${{\dot {C}}^{2}}({{\Gamma }_{\varepsilon }})$ рядом

где функции $u_{p}^{\Gamma }$ и $u_{p}^{\gamma }$ – коэффициенты рядов Тейлора (12) с , . Для $N \in {{\mathbb{Z}}_{ + }}$ верны оценки: где $i = 0,1,2,$ а C – константа, не зависящая от ε, N и f.