Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 498, № 1, стр. 71-75

1. ПОСТАНОВКА ЗАДАЧИ

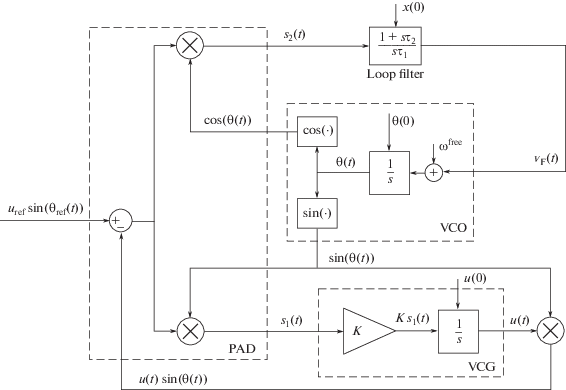
Рассмотрим схему АФАП, используемую в электроэнергетике [4] (рис. 1).

Входной сигнал имеет фазу ${{\theta }_{{ref}}}\left( t \right)$, амплитуду ${{u}_{{{\text{ref}}}}}$ > 0 и частоту $~{{\dot {\theta }}_{{{\text{ref}}}}}(t) \equiv {{\omega }_{{{\text{ref}}}}}$ > 0. Подстраиваемый генератор имеет собственную частоту ${{\omega }^{{{\text{free}}}}}~$ и формирует сигнал с фазой θ(t). Амплитуда подстраиваемого сигнала u(t) формируется с помощью интегратора с передаточной функцией $\frac{K}{s}$. Амплитудно-фазовый детектор определяет разность входного и подстраиваемого сигналов u_refsin(θ_ref(t)) – ‒ $u(t){\text{sin}}(\theta (t))$ для формирования управляющих сигналов ${{s}_{{1,2}}}(t)$, корректирующих амплитуду и фазу. Управляющий сигнал ${{s}_{2}}(t)$ дополнительно пропускается через пропорционально-интегрирующий фильтр (передаточная функция $\frac{{1 + s{{\tau }_{2}}}}{{s{{\tau }_{1}}}}$, ${{\tau }_{{1,2}}}$ > 0). До включения схемы устанавливаются начальные состояния фильтра $x\left( 0 \right) = 0$ и амплитуды $u\left( 0 \right) = {{u}_{{{\text{nom}}}}}~$ (ожидаемая амплитуда). Если на вход поступает сигнал с ${{\theta }_{{{\text{ref}}}}}\left( 0 \right) = \theta \left( 0 \right)$, ${{\omega }_{{{\text{ref}}}}} = {{\omega }^{{{\text{free}}}}}~$ и $~{{u}_{{{\text{ref}}}}} = {{u}_{{{\text{nom}}}}}$, то управляющие сигналы ${{s}_{{1,2}}}\left( t \right) \equiv 0$. В противном случае управляющие сигналы должны обеспечить процесс подстройки и переход состояния системы к стационарному (синхронному) режиму.

2. ОСНОВНОЙ РЕЗУЛЬТАТ. АНАЛИЗ УСТОЙЧИВОСТИ СИНХРОННОГО РЕЖИМА И ПЕРЕХОДНЫХ ПРОЦЕССОВ

Согласно схеме на рис. 1 получим систему неавтономных дифференциальных уравнений

Перейдем к рассмотрению отклонений состояния системы (1) от синхронного режима: y(t) = (u_e(t), x(t), ${{\theta }_{e}}(t)),$ где ${{u}_{e}}(t) = {{u}_{{{\text{ref}}}}} - u(t)$ и ${{\theta }_{e}}(t) = {{\theta }_{{{\text{ref}}}}}(t) - \theta (t)$. При предположении о полном подавлении высокочастотных компонент фильтром можно перейти к анализу автономной модели:

где $\omega _{e}^{{{\text{free}}}} = {{\omega }_{{{\text{ref}}}}} - {{\omega }^{{{\text{free}}}}}$. Система (2) имеет стационарные состояния z(t) = $({{u}_{e}}(t),x(t),{{\theta }_{e}}(t)) \equiv 0~$ вида

Стационарные состояния $z_{{{\text{st}}}}^{{{\text{eq}}}}~$ асимптотически устойчивы и совпадают со стационарными состояниями исходной неавтономной модели (1), а $z_{{{\text{un}}}}^{{{\text{eq}}}}$ – неустойчивы при всех допустимых значениях параметров схемы. Следующий результат позволяет обосновать переход от системы (1) к системе (2) для анализа устойчивости стационарного (синхронного) режима.

Лемма. Существует такое $\delta > 0$, что при ${\text{||}}{{z}_{0}} - z_{{{\text{st}}}}^{{{\text{eq}}}}{\text{||}}$ < δ выполнено соотношение $\mathop {\lim }\limits_{t~ \to + \infty } {\text{||}}y(t,{{z}_{0}})$ – – z(t, z₀)|| = 0 для достаточно большого значения ${{{{\omega }}}_{{{\text{ref}}}}}$. Для произвольных z₀, $\varepsilon > 0$ и $T~ > ~0$ при достаточно большом ${{{{\omega }}}_{{{\text{ref}}}}}$ выполнена оценка $\left| {\left| {y(t,{{z}_{0}}) - z(t,{{z}_{0}})} \right|} \right|$ < ε для $t \in \left[ {0,T} \right)$.

Схема доказательства. Рассмотрим систему (1) в виде $\dot {y} = {{(2{{\omega }_{{{\text{ref}}}}})}^{{ - 1}}}F(\tau ,y)$, где τ = $2{{\omega }_{{{\text{ref}}}}}t$, $F\left( {\tau ,y} \right)$ – 2π-периодическая функция τ. Используя метод усреднения [10], получим систему (2) $\dot {z} = \frac{1}{{2{{\omega }_{{{\text{ref}}}}}}}~~\mathop {{\text{lim}}}\limits_{L~ \to + \infty } ~\frac{1}{L}\mathop \smallint \limits_0^L F\left( {\tau ,z} \right)d\tau ~$, у которой решения близки с решениями неавтономной системы на конечном интервале времени, а устойчивые состояния равновесия совпадают с $z_{{{\text{st}}}}^{{{\text{eq}}}}$.

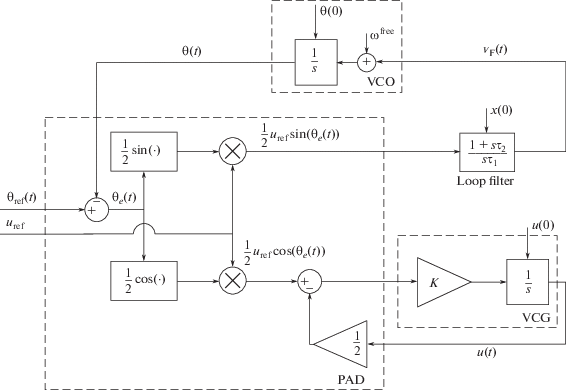
Система (2) описывает работу модели АФАП на рис. 2. Здесь блок амплитудно-фазового детектора заменен на нелинейный блок с соответствующими характеристиками, на вход которого поступают амплитуда и фаза входного сигнала; выходом подстраиваемого генератора является фаза подстраиваемого сигнала.

Для анализа глобальной устойчивости отдельных и связанных систем автоподстройки естественными являются развитие и применение методов функций Ляпунова (см., например, [11–13]).

Теорема 1. Все решения системы (2) стремятся к стационарному множеству (3).

Доказательство. Уравнения для x(t) и ${{{{\theta }}}_{e}}(t)$ в системе (2) не зависят от ${{u}_{e}}\left( t \right)$. Используя теорему [11] о глобальной устойчивости систем с цилиндрическим фазовым пространством и функцию Ляпунова

получим, что $x(t) \to {{\tau }_{1}}\omega _{e}^{{{\text{free}}}}~$ и ${{\theta }_{e}}\left( t \right) \to \pi k~$ при $t \to + \infty $. Тогда при $t \to + \infty .$

Для заданных допустимых диапазонов отклонения частоты $\left| {\omega _{e}^{{{\text{free}}}}} \right| \in [0,\omega _{e}^{{{\text{max}}}})$ и входной амплитуды ${{u}_{{{\text{ref}}}}} \in \left[ {{{u}_{{{\text{min}}}}},{{u}_{{{\text{max}}}}}} \right)$ решим задачу определения в системе (2) наибольшего отклонения разности фаз $\theta _{e}^{{{\text{max}}}}$ (максимальной расфазировки) на переходных процессах при мгновенном изменении частоты ${{\omega }_{{{\text{ref}}}}}$ и амплитуды ${{u}_{{{\text{ref}}}}}$ входного сигнала внутри заданных диапазонов: $\theta _{e}^{{{\text{max}}}} = {\text{su}}{{{\text{p}}}_{{t > 0}}}\left| {{{\theta }_{e}}(0) - {{\theta }_{e}}(t)} \right|$.

Теорема 2. Если выполнено условие

то

Схема доказательства. Пусть система находилась в устойчивом стационарном состоянии при $\omega _{e}^{{{\text{free}}}} = \omega _{e}^{{{\text{max}}}} > 0~$ и ${{u}_{{{\text{ref}}}}} = {{u}_{1}}$, а после изменения параметров входного сигнала на $\omega _{e}^{{{\text{free}}}} = - {\kern 1pt} \omega _{e}^{{{\text{max}}}}$ < 0 и ${{u}_{{{\text{ref}}}}} = {{u}_{2}}$ перешла в новое устойчивое стационарное состояние. Рассмотрим линии уровня функции Ляпунова (4) для уравнений системы (2) относительно $\left( {x,{{\theta }_{e}}} \right)$ после переключения:

Тогда при

линия уровня $V\left( {x,{{\theta }_{e}}} \right) = {{c}^{{{\text{max}}}}}$ является замкнутой и содержит состояние равновесия $(\omega _{e}^{{{\text{max}}}}{{\tau }_{1}},0)$ системы до переключения (рис. 3).

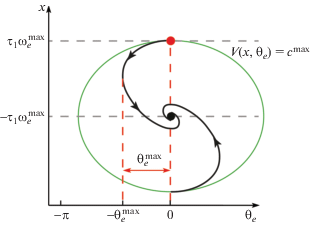
Поскольку построенная замкнутая область является положительно инвариантной, то координата ${{\theta }_{e}}(t)$ траекторий с начальными данными из этой области не превысит максимальной координаты ${{\theta }_{e}}(t)$ среди точек области. Из монотонности оценки по u₂ получаем утверждение теоремы.

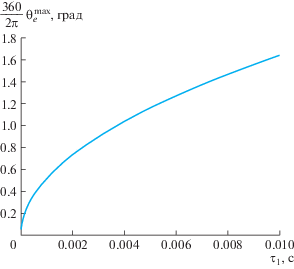
Заметим, что если условие (5) не выполнено, то рассматриваемая линия уровня будет не замкнутой и предложенная техника не позволяет провести аналитическую оценку. При этом теорема 1 обеспечивает отсутствие скрытых колебаний [14, 15] в фазовом пространстве системы, что позволяет проводить достоверные численные оценки. Пусть необходимо при известном диапазоне изменения частоты ${{\omega }_{{{\text{ref}}}}} \in 2\pi \,[47.5,~52.5]~$ рад/c и амплитуды напряжения ${{u}_{{{\text{ref}}}}} \in [24,~43.8]$ кВ контактной сети определить эффективные параметры АФАП¹¹. Положим собственную частоту подстраиваемого генератора равной номинальной ${{\omega }^{{{\text{free}}}}}$ = 2π × 50 рад/c. Тогда $\omega _{e}^{{{\text{free}}}} \in 2\pi \,[ - 2.5,~2.5]~$ рад/c. Из оценки (6) на рис. 4 следует, что, например, для желаемой расфазировки в три градуса [7] можно взять ${{\tau }_{1}} \leqslant 0.025$. В инженерной литературе для уменьшения расфазировки часто берут значительно меньшие значения ${{\tau }_{1}}$ (например, ${{\tau }_{1}} = $ 0.00005 [4, с. 18]). Однако уменьшение ${{\tau }_{1}}$ может приводить к существенному уменьшению соотношения сигнал/шум и деградации работоспособности системы [8, с. 132]. В заключение отметим, что блок-схемы на рис. 1 и 2 могут быть реализованы в виде цифровых алгоритмов на микроконтроллере. Для этого от системы с непрерывным временем можно перейти к системе с дискретным временем, применив, например, метод Эйлера или Тастина.