Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 499, № 1, стр. 58-62

1. ПОСТАНОВКА ЗАДАЧИ

При экспериментальном исследовании тепловых процессов нередко возникают ситуации, когда невозможно определить требуемую физическую величину путем проведения прямых измерений. В таких случаях прибегают к решению обратных задач, и интересующие характеристики восстанавливаются по результатам косвенных измерений [1, 2].

Рассматриваемая в работе обратная задача посвящена определению зависящего от температуры коэффициента теплопроводности вещества по результатам экспериментального наблюдения за динамикой температурного поля в объекте и (или) теплового потока на поверхности объекта. Предложен новый эффективный алгоритм решения этой обратной задачи, одним из важных элементов которого является методология быстрого автоматического дифференцирования (БАД-методология).

Рассматривается область $Q \subset {{R}^{n}}$ с кусочно-гладкой границей $S$, заполненная исследуемым веществом. Динамика температурного поля в веществе описывается решением следующей начально-краевой задачи:

Здесь $x = ({{x}_{1}},\; \ldots ,\;{{x}_{n}})$ – декартовы координаты; t – время; $T(x,t)$ – температура вещества в точке с координатами x в момент времени t; $C(x)$ – объемная теплоемкость вещества; $K(T)$ – коэффициент теплопроводности; ${{w}_{0}}(x)$ – заданная температура вещества в начальный момент времени t = 0; ${{w}_{S}}(x,t)$ – заданная температура на границе области. Объемная теплоемкость $C(x)$ считается известной функцией координат.

Если коэффициент теплопроводности $K(T)$ известен, то, решив прямую задачу (1)–(3), найдем распределение температуры $T(x,t)$ в $Q \times (0,\Theta ]$. Если же функция $K(T)$ неизвестна, то ее определение представляет большой интерес. Обратная коэффициентная задача сводится к следующей вариационной задаче: требуется найти такую зависимость коэффициента теплопроводности вещества $K(T)$ от температуры T, при которой температурное поле $T(x,t)$ и потоки тепла $\left( { - K(T(x,t))\frac{{\partial T(x,t)}}{{\partial{ \bar {n}}}}} \right)$ на границе объекта, полученные в результате решения прямой задачи (1)–(3), мало отличаются от температурного поля $Y(x,t)$ и потока тепла $P(x,t)$, полученных экспериментально. Мерой отклонения этих функций может служить величина

где $\mu (x,t) \geqslant 0$, $\beta (x,t) \geqslant 0$ и $\varepsilon \geqslant 0$ – заданные весовые параметры; $Y(x,t)$ – заданное температурное поле; $P(x,t)$ – заданный тепловой поток на границе $S$ области $Q$, $\frac{{\partial T}}{{\partial n}}$ – производная температуры по направлению внешней нормали к границе $S$ области $Q$.

2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Подобные задачи оптимального управления обычно решаются численно с помощью некоторого метода спуска, который требует знания градиента функционала. При этом крайне важно определять точное значение этого градиента. Было получено аналитическое выражение градиента целевого функционала для сформулированной здесь задачи в $n$-мерной постановке. Однако использовать это аналитическое выражение при численном решении задачи практически невозможно в силу его сложности. В предлагаемом алгоритме для вычисления градиента функционала использовалась эффективная БАД-методология. Эффективность этой методологии обеспечивается использованием решения сопряженной задачи. Основным достоинством БАД-методологии является автоматическое построение такой аппроксимации сопряженной задачи, которая согласованна с выбранной аппроксимацией прямой задачи.

Важным элементом алгоритма решения обратной коэффициентной задачи является решение прямой задачи (1)–(3). От эффективности ее решения зависит эффективность решения обратной задачи в целом. Для аппроксимации уравнения теплопроводности в одномерном случае применялась двухслойная неявная схема с весами.

При использовании БАД-методологии аппроксимация сопряженной задачи однозначно определяется выбором аппроксимации прямой задачи, и при переходе от одномерного случая к многомерному влияние этого выбора становится более весомым. Так, если начально-краевая задача в двумерном случае аппроксимируется неявной схемой с весами, аппроксимация сопряженной задачи будет представлять собой линейную систему алгебраических уравнений, для разрешения которой (в силу двумерности по пространству) также требуется строить итерационный процесс. Поэтому для решения прямой задачи в многомерном случае рекомендуется использовать схемы переменных направлений [3, 4]. При дискретизации двумерной начально-краевой задачи была выбрана безусловно устойчивая (n = 2) схема Писмена–Рекфорда [5].

Алгоритм решения прямой задачи в трехмерном случае заметно усложняется и требует больших затрат машинного времени. В [6] на примере ряда нелинейных задач для трехмерного уравнения теплопроводности проводится сравнительный анализ нескольких схем переменных направлений. При сравнении методов принимались во внимание точность получаемого решения и время достижения требуемой точности.

Сопряженные уравнения и формула для вычисления градиента целевого функционала, использовавшиеся при решении обратной задачи в трехмерном случае, получены для случая работы с локально-одномерной схемой. Для других схем эти формулы можно получить аналогичным образом.

Для численного решения задачи вводилась временнáя и пространственная сетки. В каждом сеточном узле расчетной области $\bar {Q} \times [0,\Theta ]$ все функции определялись своими точечными значениями. Отрезок [a, b], на котором идентифицировалась функция $K(T)$, определялся как множество значений заданных функций ${{w}_{0}}(x)$ и ${{w}_{S}}(x,t)$. Этот отрезок разбивался точками ${{\tilde {T}}_{0}} = a$, ${{\tilde {T}}_{1}}$, ${{\tilde {T}}_{2}}$, …, ${{\tilde {T}}_{M}}$ = b на $M$ частей. Каждой из точек ${{\tilde {T}}_{m}}$ ($m = 0$, ..., M) ставилось в соответствие число ${{k}_{m}} = K({{\tilde {T}}_{m}})$. Искомая функция $K(T)$ аппроксимировалась непрерывной кусочно-линейной функцией с узлами в точках $\{ ({{\tilde {T}}_{m}},{{k}_{m}})\} _{{m = 0}}^{M}$, так что

K(T) = k_{m – 1} + $\frac{{{{k}_{m}} - {{k}_{{m - 1}}}}}{{{{{\tilde {T}}}_{m}} - {{{\tilde {T}}}_{{m - 1}}}}}(T - {{\tilde {T}}_{{m - 1}}})$

при ${{\tilde {T}}_{{m - 1}}} \leqslant T \leqslant {{\tilde {T}}_{m}}$ (m = 1, ..., M).

Целевой функционал (4) аппроксимировался функцией $F({{k}_{0}},{{k}_{1}},\; \ldots ,\;{{k}_{N}})$ конечного числа переменных с помощью метода прямоугольников. Минимизация этой функции проводилась численно с помощью градиентных методов. Использование БАД-методологии позволило добиться того, что градиент целевой функции в предложенном алгоритме вычислялся с машинной точностью, что увеличивало скорость минимизации функционала.

Проведенные численные эксперименты показали, что качество восстановления коэффициента теплопроводности сильно зависит от распределения “экспериментальных” данных. Бывают случаи, когда на некоторых участках отрезка $[a,b]$ слишком мало данных, необходимых для идентификации коэффициента теплопроводности. Для анализа распределения экспериментальных данных по интервалам отрезка температур [a, b] вводится функция ${{W}_{*}}(T)$ – относительная мера той под-области области $Q \times (0,\Theta )$, температура в точках которой меньше T. При решении конкретных задач необходимо предварительно проанализировать плотность распределения функции ${{W}_{*}}(T)$.

Было выявлено, что коэффициент теплопроводности не идентифицируется регулярным способом для тех значений T, при которых плотность распределения экспериментальных данных мала. Для его определения в таких точках требуется проведение дополнительных исследований или введение дополнительных предположений.

Отметим также, что в многомерном случае градиент целевого функционала распределен по температуре сильно неравномерно. Это приводит к ухудшению сходимости итерационного процесса в целом. Для ускорения итерационного процесса предложен подход, основанный на последовательном увеличении числа M разбиений отрезка [a, b] [5]. Начинать процесс желательно с M = 1. Полученное решение следует использовать в качестве начального приближения для варианта с M = 2 и т.д.

Задача оптимального управления (1)–(4) может быть рассмотрена в двух крайних постановках. Если в целевом функционале $\beta (x,t) = 0$, то в качестве экспериментальных данных в задаче выступает заданное температурное поле (функционал “поле”). Если в (4) $\mu (x,t) = 0$, то в качестве экспериментальных данных выступает заданный тепловой поток на поверхности рассматриваемого объекта (функционал “поток”).

При исследовании обратной задачи с $\beta (x,t) = 0$ (функционал “поле”) большое внимание уделялось практически важному случаю, когда температурное поле задано только в части рассматриваемого объекта. Анализ результатов решения большого числа обратных коэффициентных задач показал, что при использовании функционала “поле” обратная задача может иметь неединственное решение. Будет решение обратной задачи единственным или нет – существенно зависит от заданного экспериментального поля $Y(x,t)$. Ответ на вопрос, в каких случаях возможно появление неединственности решения сформулированной обратной коэффициентной задачи, может дать следующее утверждение.

Лемма. Пусть функция Y(x, t) ∈ $C_{{x,t}}^{{2,1}}(G)$ ∩ ${{C}^{1}}(\bar {G})$ является решением прямой задачи (1)–(3) при двух допустимых коэффициентах теплопроводности ${{K}_{1}}(T) \in {{C}^{1}}([a,b])$ и ${{K}_{2}}(T) \in {{C}^{1}}\left( {[a,b]} \right)$, $T \in [a,b]$. Тогда 

а) найдется функция $R(T) \in C\left( {[a,b]} \right)$ такая, что

б) при такой функции $Y(x,t)$ решений $K(T)$ обратной задачи бесконечно много.

Доказательство этого утверждения в n-мерном случае аналогично тому, которое приводится в [5] для двумерного случая.

В этом случае рекомендуется решать задачу идентификации коэффициента теплопроводности несколько раз, выбирая в качестве начального приближения каждый раз новую функцию. Если при этом получается одно и то же решение задачи оптимального управления, то его можно считать решением задачи идентификации. Если же решение задачи будет зависеть от выбора начального приближения, то необходимо задать дополнительное условие, например, задавать точку, в которой искомый коэффициент теплопроводности известен.

Необходимо отметить, что при исследовании большого числа задач с функционалом “поток” никогда не приходилось сталкиваться с неединственностью решения.

Известно, что в окрестности решения градиентные методы сходятся довольно медленно. Поэтому в работе исследовалась возможность применения оптимизационных методов второго порядка сходимости для решения рассматриваемой обратной коэффициентной задачи.

Так как рассматриваемый в работе функционал имеет квадратичный вид, то наиболее подходящим оптимизационным методом второго порядка сходимости в этом случае представляется метод Левенберга–Марквардта. При использовании этого метода вводится дополнительная вектор-функция $\overline U = \left\{ {{{U}_{d}}} \right\}_{{n = 1}}^{D}$ ($D$ – количество квадратичных слагаемых в функционале), элементы которой – квадратный корень каждого слагаемого целевого функционала. Далее строится матрица Якоби $\Omega = \left\{ {{{\Omega }_{{dm}}}} \right\}$ вектор-функции $\overline U $. Каждая d-я строка матрицы $\Omega $ – это градиент функции ${{U}_{d}}$ относительно компонент вектора управления k₀, ${{k}_{1}}, \ldots ,{{k}_{M}}$.

Точность вычисления элементов матрицы типа Якоби оказывает заметное влияние на сходимость метода Левенберга–Марквардта. Существенным в предлагаемом подходе является то, что элементы матрицы типа Якоби вычисляются с машинной точностью благодаря использованию БАД-методологии.

Согласно алгоритму Левенберга–Марквардта вектор управления ${\mathbf{k}} = \left\{ {{{k}_{m}}} \right\}_{{m = 0}}^{M}$ меняется на каждой последующей итерации $(s + 1)$ по формуле: ${{k}_{{s + 1}}} = {{k}_{s}} + {{r}_{s}}$. Направление спуска ${{r}_{s}}$ определяется как решение следующей системы линейных алгебраических уравнений:

На основании проведенных исследований предлагается рассчитывать константы ${{\lambda }_{s}}$ для рассматриваемой обратной задачи по формуле

где $\alpha > 0$ – некоторая константа, зависящая от задачи.

Для проверки работоспособности и эффективности предложенного алгоритма было решено большое количество тестовых задач. Во всех рассмотренных случаях коэффициент теплопроводности восстанавливался с высокой точностью.

В качестве примера приведем задачу определения коэффициента теплопроводности вещества при следующих входных данных: в качестве начальной функции ${{w}_{0}}(x,y,z)$ и граничной функции ${{w}_{\Gamma }}(x,y,z,t)$ выбраны следы функции $\Lambda (x,y,z,t)$ = = $\sqrt {\frac{{9 \cdot {{{(x + 1)}}^{2}} + 20{{y}^{2}} + 25{{z}^{2}}}}{{9 - 8t}}} $ на параболической границе области $Q \times (0,\;\Theta )$ = $(0,1) \times (0,1) \times (0,1)$ × (0, 1). Анализ входных данных позволил определить диапазон изменения температуры: a = 1, b = 9. В качестве “экспериментальных” данных использовался поток тепла, вычисленный по температурному полю, полученному в результате решения прямой задачи (1)–(3) при $C(x) = 1$ и с коэффициентом теплопроводности: k(T) = $\left\{ \begin{gathered} 0.1 \cdot (T - 3) \cdot (T - 6) \cdot (T - 7) + 3.4,\,\,\,T \geqslant 3, \hfill \\ 1.2 \cdot (T - 3) + 3.4,\quad T < 3. \hfill \\ \end{gathered} \right.$

Анализ распределения “экспериментальных” данных показал, что на правом конце отрезка [1.0, 9.0] практически нет “экспериментальных” данных. Проведенные расчеты показали, что при равномерном разбиении отрезка температур на M = 64 интервала последняя компонента вектора градиента равнялась нулю с машинной точностью, т.е. коэффициент теплопроводности можно идентифицировать лишь на отрезке [1.0, 8.875].

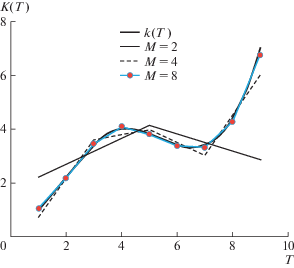
Процесс построения решения задачи идентификации проиллюстрирован на рис. 1. Там представлены функция $k(T)$ и оптимальные управления, полученные при $M = 2,4,8$. Видно, что опорные точки кусочно-линейного оптимального управления, полученного при $M = 8$, почти лежат на “теоретической” линии $K(T) = k(T)$.

График оптимального управления, полученного при $M = 64$, совпадает с графиком функции $k(T)$. Максимальное отклонение рассчитанного коэффициента теплопроводности ${{K}_{{opt}}}(T)$ от его аналитического значения $K(T) = k(T)$ на отрезке [1.0, 8.875] составляет 1.3914 × 10^–7.

Для всех рассмотренных примеров было проведено численное исследование устойчивости получаемых решений. “Экспериментальные” данные возмущались с помощью генератора случайных чисел. Необходимо отметить, что использование небольшого количества разбиений отрезка температур ($M \leqslant 15$) действует как сглаживающий фактор при решении задачи. При умеренном возмущении “экспериментальных” данных осцилляции в решении задачи появляются, когда отрезок температур разбивается на большое количество интервалов ($M \geqslant 20$).

Анализ проведенных исследований показал, что возмущения в решениях задач, полученные с помощью предложенного алгоритма, имеют тот же порядок, что и вызвавшие их возмущения в экспериментальных данных. При малых возмущениях в экспериментальных данных (до 10%) осцилляции в решениях задач практически незаметны даже при большом количестве M разбиений отрезка температур.

При умеренных возмущениях в экспериментальных данных (10–25%) необходимо решать оптимизационную задачу с функционалом, в котором присутствует регуляризатор, т.е. в целевом функционале параметр $\varepsilon > 0$.