Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 499, № 1, стр. 26-30

Эквациональный класс алгебр Магари был введен Р. Магари [5] для изучения понятия доказуемости в данной формальной теории в более общем алгебраическом контексте. Алгебра Магари – это булева алгебра $(\mathcal{B},\square )$ с унарным оператором $\square $, которая удовлетворяет следующим тождествам: $\square (a \to b) \to (\square a \to \square b) = \top $, $\square (\square a \to a) \to \square a = \top $ и $\square \top \, = \, \top $, где $ \top $ есть единица алгебры $\mathcal{B}$.

С данной формальной теорией T (в рамках которой можно выразить синтаксические понятия, связанные с языком этой теории, и, в частности, понятие доказуемости) можно связать конкретную алгебру Магари ${{\mathfrak{D}}_{T}}$, называемую алгеброй доказуемости теории $T$, которая определяется как $({{\mathfrak{L}}_{T}},{{\square }_{T}})$, где ${{\mathfrak{L}}_{T}}$ есть алгебра Линденбаума теории $T$, а ${{\square }_{T}}$ есть унарный оператор, индуцируемый предикатом доказуемости $\mathop {{\text{Pr}}}\nolimits_T (x)$ в теории $T$, т.е. формулой в языке теории $T$, выражающей, что формула с гёделевым номером $x$ является теоремой теории $T$, следующим образом

где $\varphi {{ \sim }_{T}}\psi \Leftrightarrow T \vdash \varphi \leftrightarrow \psi $.

Формальное изучение понятия доказуемости как оператора (или модальности) традиционно относят к области, известной как логика доказуемости. Алгебры доказуемости позволяют взглянуть на вопросы, изучаемые в рамках этой области, с алгебраической точки зрения. Одним из центральных результатов в логике доказуемости является знаменитая теорема Р. Соловея об арифметической полноте [11], которая может быть переформулирована на алгебраическом языке следующим образом: для каждой ${{\Sigma }_{1}}$-корректной теории T эквациональная теория алгебры ${{\mathfrak{D}}_{T}}$ аксиоматизируется пропозициональной модальной логикой Гёделя–Лёба ${\text{GL}}$.

Наиболее сильные результаты об алгебрах доказуемости формальных теорий были получены В.Ю. Шавруковым [7–10]. Среди них неарифметичность полной первопорядковой теории ${\text{Th}}({{\mathfrak{D}}_{T}})$ алгебры доказуемости любой ${{\Sigma }_{1}}$-корректной теории $T$ и неразрешимость ее $\forall {\text{*}}\exists {\text{*}}\forall {\text{*}}\exists {\text{*}}$-фрагмента, полное описание рекурсивно перечислимых подалгебр ${{\mathfrak{D}}_{T}}$ (впоследствии Д. Замбелла распространил этот результат на произвольные подалгебры), существование нетривиальных автоморфизмов алгебры ${{\mathfrak{D}}_{T}}$. Шавруковым также были получены несколько важных результатов об изоморфизмах алгебр доказуемости [7, 9]. Именно эти результаты, формулируемые ниже, являются объектом исследований данной работы.

Первый из них – это достаточное условие отсутствия элементарной эквивалентности (а значит, и изоморфизма) алгебр доказуемости двух ${{\Sigma }_{1}}$-корректных теорий (см. [7] и [10, Theorem 2.11]). В частности, отсюда вытекает неизоморфизм алгебр доказуемости арифметики Пеано и теории множеств Цермело–Френкеля.

Теорема 1. Если теория $T$ доказывает схему ${\text{RF}}{{{\text{N}}}_{{{{\Sigma }_{1}}}}}(S)$ равномерной ${{\Sigma }_{1}}$-рефлексии для теории S, то 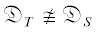. Более того, в этом случае ${{\mathfrak{D}}_{T}}$ и ${{\mathfrak{D}}_{S}}$ не являются элементарно эквивалентными.

Отметим, что в силу результата Крипке и Пур-Эль [6] для достаточно широкого класса теорий T и S алгебры Линденбаума ${{\mathfrak{L}}_{T}}$ и ${{\mathfrak{L}}_{S}}$ рекурсивно изоморфны. Второй важный результат Шаврукова [9] – это достаточное условие существования (рекурсивного) изоморфизма между ${{\mathfrak{D}}_{T}}$ и ${{\mathfrak{D}}_{S}}$, точную формулировку которого мы здесь не приводим.

Впоследствии Г. Адамссон усилил теорему 1 и получил следующий результат [1] (мы приводим другую, но, в силу результатов [1, Theorem 17], эквивалентную формулировку). Здесь ${{\mathcal{R}}_{T}}(x)$ есть функция ${{\Sigma }_{1}}$-рефлексии теории T, которая определяется следующим образом. Значение ${{\mathcal{R}}_{T}}(x)$ есть наименьшая верхняя граница для минимальных свидетелей ${{\Sigma }_{1}}$-предложений, которые доказуемы в T доказательствами с гёделевыми номерами, не превосходящими x.

Теорема 2. Если существует эпиморфизм из ${{\mathfrak{D}}_{T}}$ на ${{\mathfrak{D}}_{S}}$, то существует элементарная функция $t(x)$ такая, что неравенство

имеет место для бесконечно многих $n \in \mathbb{N}$.

Отметим, что это усиливает теорему Шаврукова о неизоморфизме в двух направлениях. Во-первых, ослаблено само достаточное условие неизоморфизма, что позволило построить примеры, демонстрирующие, что алгебра ${{\mathfrak{D}}_{T}}$ действительно зависит от конкретного выбора предиката доказуемости для теории T. В частности, Адамссон установил [1, Corollary 21], что 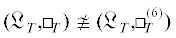, где $\square _{T}^{{(6)}}$ есть 6-кратная итерация оператора ${{\square }_{T}}$. Во-вторых, это условие гарантирует отсутствие эпиморфизма (а не просто изоморфизма). В своей работе Адамссон отмечает, что полученное им условие не является оптимальным и возможны более точные оценки.

Настоящая работа является продолжением исследований в этом направлении. Наш основной результат (теорема 3) усиливает приведенный выше результат Адамссона. Мы доказываем несколько свойств функции рефлексии ${{\mathcal{R}}_{T}}(x)$ для теории T, которые затем используются для получения более точных оценок в условии неизоморфизма, а также вводим классы функций $\mathcal{F}_{T}^{k}(U)$, которые являются обобщениями класса доказуемо тотальных вычислимых функций $\mathcal{F}(T)$ и позволяют обобщить основной результат. Используя усиленный результат о неизоморфизме, мы доказываем 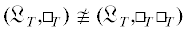, что подтверждает одну из гипотез из работы [1], а также получаем серию новых примеров пар теорий с неизоморфными алгебрами доказуемости, но совпадающими классами доказуемо тотальных вычислимых функций.

В настоящей работе мы рассматриваем теории первого порядка в языке арифметики. Базовой арифметической теорией является элементарная арифметика EA, т.е. теория первого порядка в языке $0,( \cdot ){\text{'}}, + , \times $, расширенном одноместным функциональным символом $exp$ для функции 2^x. Теория EA задается стандартным набором аксиом, определяющих эти символы, и схемой индукции для всех элементарных формул (или ${{\Delta }_{0}}(exp)$-формул), т.е. формул в языке с экспонентой, все вхождения кванторов в которые ограничены термами в этом языке. Через EA⁺ обозначается теория, расширяющая EA аксиомой, выражающей тотальность суперэкспоненциальной функции $2_{y}^{x}$. Классы арифметической иерархии ${{\Sigma }_{n}}$ и ${{\Pi }_{n}}$ в чисто арифметическом языке без экспоненты рекурсивно определяются стандартным образом для всех $n \in \mathbb{N}$. Для заданного класса формул $\Gamma $ две теории T и $S$ называются $\Gamma $-эквивалентными, если они доказывают одни и те же формулы из $\Gamma $.

Мы предполагаем фиксированной стандартную арифметизацию синтаксиса. В частности, $ \ulcorner \varphi \urcorner $ обозначает гёделев номер формулы $\varphi $. Все теории, рассматриваемые в этой работе, предполагаются элементарно аксиоматизируемыми ${{\Sigma }_{1}}$-корректными расширениями теории ${\text{EA}}$. Напомним, что ${{\Sigma }_{1}}$-корректность означает истинность любого ${{\Sigma }_{1}}$-предложения, доказуемого в T. Каждая теория T задается элементарной формулой ${{\sigma }_{T}}(x)$, определяющей множество (гёделевых номеров) аксиом теории T в стандартной модели арифметики $\mathbb{N}$. Эта формула используется в построении (упомянутых выше) стандартного предиката доказательства $\mathop {{\text{Prf}}}\nolimits_T (p,x)$ и связанного с ним предиката доказуемости $\exists p{\text{Pr}}{{{\text{f}}}_{T}}(p,x)$, который мы обозначаем через ${{\square }_{T}}(x)$. Конечные итерации предиката ${{\square }_{T}}$ обозначаются через $\square _{T}^{{(k)}}$. Стандартный предикат доказуемости ${{\square }_{T}}$ удовлетворяет условиям Лёба и обладает свойством доказуемой ${{\Sigma }_{1}}$-полноты, что гарантирует истинность тождеств, задающих класс алгебр Магари, в определенной выше алгебре доказуемости ${{\mathfrak{D}}_{T}}$ (см. [4]).

Среди расширений заданной теории T мы рассматриваем так называемые схемы рефлексии. Схема локальной $\Gamma $-рефлексии $\mathop {{\text{Rfn}}}\nolimits_\Gamma (T)$ задается множеством формул вида ${{\square }_{T}}\gamma \to \gamma $, для каждого предложения $\gamma \in \Gamma $. Схема равномерной $\Gamma $-рефлексии ${\text{RF}}{{{\text{N}}}_{\Gamma }}(T)$ задается множеством формул вида $\forall x\left( {{{\square }_{T}}\gamma (\underline x ) \to \gamma (x)} \right)$, для каждой формулы $\gamma \in \Gamma $. Обычно класс $\Gamma $ есть один из классов арифметической иерархии.

Функция $f{\text{:}}\;{{\mathbb{N}}^{k}} \to \mathbb{N}$ называется доказуемо тотальной вычислимой функцией в теории T, если существует ${{\Sigma }_{1}}$-формула $\psi ({{x}_{1}},\; \ldots ,\;{{x}_{k}},y)$, определяющая график функции f в стандартной модели, такая, что

Класс доказуемо тотальных вычислимых функций теории T обозначается через $\mathcal{F}(T)$. Известно, что $\mathcal{F}({\text{EA}}) = {{\mathcal{E}}_{3}}$ есть класс функций элементарных по Кальмару. Будем говорить, что функция $g(x)$ мажорирует функцию $f(x)$, если неравенство $f(n) > g(n)$ выполнено только для конечного множества натуральных чисел $n \in \mathbb{N}$. Выражение ${{f}^{{(n)}}}(x)$ обозначает $n$-кратную композицию функции $f(x)$ с собой, и${{f}^{{(0)}}}(x) = x$.

В работе [1] вводится несколько функций, связанных с “ускорением” доказательств при добавлении к теории T некоторых допустимых правил вывода (и других принципов), например, правила Париха (из ${{\square }_{T}}\psi $ вывести $\psi $), и доказывается, что они имеют одинаковую скорость роста. В исходной формулировке теоремы 2 фигурирует другая функция, но как было упомянуто выше, использование функции ${{\Sigma }_{1}}$-рефлексии ${{\mathcal{R}}_{T}}(x)$ приводит к эквивалентной формулировке.

Поскольку теория T является ${{\Sigma }_{1}}$-корректной, функция ${{\mathcal{R}}_{T}}(x)$ тотальна и вычислима. Как отмечается в [1], функция ${{\mathcal{R}}_{T}}(x)$ близка к тому, чтобы быть доказуемо тотальной вычислимой функцией теории T, хотя и не является таковой (см. утверждение 1). Определение следующих классов функций $\mathcal{F}_{T}^{k}(U)$ базируется на этом наблюдении. Обозначим через ${{\mathcal{F}}_{T}}(U)$ класс всех функций $f{\text{:}}\;{{\mathbb{N}}^{n}} \to \mathbb{N}$ таких, что

для некоторой ${{\Sigma }_{1}}$-формулы ${{\psi }_{f}}({{x}_{1}},\; \ldots ,\;{{x}_{n}},y)$, определяющей график функции f в стандартной модели. Аналогично определяются классы $\mathcal{F}_{T}^{k}(U)$ при $k \geqslant 1$, где используется итерированный предикат доказуемости $\square _{T}^{{(k)}}$ вместо ${{\square }_{T}}$. Мы также пишем $\square _{T}^{{(0)}}\psi (\underline x )$ вместо $\psi (x)$, хотя $\square _{T}^{{(0)}}(x)$, вообще говоря, не является формулой. Тогда естественно определить $\mathcal{F}_{T}^{0}(U)$ как $\mathcal{F}(U)$. В силу доказуемой ${{\Sigma }_{1}}$-полноты имеют место следующие включения: а также $\mathcal{F}(T)\, \subseteq \,{{\mathcal{F}}_{T}}({\text{EA}})$, поскольку ${\text{EA}}\, \vdash \,{{\square }_{T}}\forall x\psi (x)$ → → $\forall x{{\square }_{T}}\psi (\underline x )$. Таким образом, мы получаем расширяющуюся цепочку классов, которые, вообще говоря, не замкнуты относительно суперпозиции (в отличие от класса $\mathcal{F}(U)$ доказуемо тотальных вычислимых функций). Однако имеет место следующее свойство замкнутости.

Лемма 1. Если теория $T$ содержит U, то для всех $F(x) \in \mathcal{F}_{T}^{m}(U)$ и $G(x) \in \mathcal{F}_{T}^{n}(U)$ имеет место $G(F(x)) \in \mathcal{F}_{T}^{{m + n}}(U)$ для всех $m,n \in \mathbb{N}$.

Следующее утверждение является переформулировкой упомянутого выше утверждения про функцию ${{\mathcal{R}}_{T}}(x)$, доказанного в [1].

Утверждение 1. Для всех $k \in \mathbb{N}$, $\mathcal{R}_{T}^{{(k)}}(x)$ ∈ ∈ $\mathcal{F}_{T}^{k}({\text{EA}})$.

Ниже мы приводим без доказательства несколько фактов о свойствах функции рефлексии ${{\mathcal{R}}_{T}}(x)$ и о классах $\mathcal{F}_{T}^{k}(U)$, которые используются в доказательстве основной теоремы настоящей работы для получения более точных оценок в условии неизоморфизма Адамссона.

Лемма 2. Существует строго монотонная элементарная функция ${v}(x)$ такая, что для всех $\psi $, $\chi $ и $n \in \mathbb{N}$, если существует $S$-вывод формулы ${{\square }_{S}}\psi \vee \,{{\square }_{S}}\chi $ с гёделевым номером, не превосходящим $n$, то либо существует $S$-вывод $\psi $, либо существует S-вывод $\chi $ с гёделевым номером, не превосходящим ${{\mathcal{R}}_{S}}({v}(n))$.

Лемма 3. Существует элементарная функция $w(x,y)$ такая, что для любой $f(x) \in \mathcal{F}(T)$ существует $c \in \mathbb{N}$ такое, что $f({{\mathcal{R}}_{S}}(n)) \leqslant {{\mathcal{R}}_{S}}(w(c,n))$ имеет место для всех $n \in \mathbb{N}$.

Следствие 1. Существует строго монотонная элементарная функция $h(x)$ такая, что для любых $k \in \mathbb{N}$ и $f(x) \in \mathcal{F}(T)$ неравенство

выполнено для почти всех $n \in \mathbb{N}$.

Следующая теорема является основным результатом нашей работы и усиливает теорему 2.

Теорема 3. Пусть $T$ и $S$ – теории со стандартными предикатами доказуемости ${{\square }_{T}}$ и ${{\square }_{S}}$. Если существует эпиморфизм алгебры ${{\mathfrak{D}}_{T}}$ на алгебру ${{\mathfrak{D}}_{S}}$, то существует элементарная функция $q(x)$ такая, что для всех $k \in \mathbb{N}$ и для любой функции $F(x) \in \mathcal{F}_{T}^{k}(T)$ неравенство $F(n) \leqslant \mathcal{R}_{S}^{{(k + 1)}}(q(n))$ выполнено для бесконечно многих $n \in \mathbb{N}$.

Мы не приводим здесь доказательства этой теоремы. Отметим лишь, что оно во многом следует доказательству Адамссона [1] (которое, в свою очередь, следует исходному доказательству Шаврукова [7]), а сформулированные выше леммы позволяют получить более точные оценки и более общий результат. Теорема 3 дает несколько достаточных условий неизоморфизма алгебр доказуемости, которые приводятся ниже.

Следствие 2. Каждое из следующих условий влечет отсутствие эпиморфизмов из ${{\mathfrak{D}}_{T}}$ на ${{\mathfrak{D}}_{S}}$:

(i) $\mathcal{R}_{S}^{{(k + 1)}}(x) \in \mathcal{F}_{T}^{k}(T)$ для некоторого $k \in \mathbb{N}$;

(ii) $\mathcal{F}_{S}^{{k + 1}}({\text{EA}}) \subseteq \mathcal{F}_{T}^{k}(T)$ для некоторого $k \in \mathbb{N}$;

(iii) $T \vdash \forall \sigma \in {{\Sigma }_{1}}(\square _{S}^{{(k + 1)}}\sigma \to \,\square _{T}^{{(k)}}\sigma )$ для некоторого $k \in \mathbb{N}$.

Отметим, что пункты (ii) и (iii) этого следствия также применимы к алгебрам для теорий с нестандартными предикатами доказуемости (например, ${{\square }_{T}}{{\square }_{T}}$) при условии, что эти предикаты могут быть заменены стандартными предикатами, которые эквивалентны исходным, и эта эквивалентность доказуема в теории EA.

Рассмотрим несколько применений теоремы 3 для получения новых примеров пар теорий с неизоморфными алгебрами. Для доказательства неизоморфизма (и отсутствия эпиморфизмов) мы будем пользоваться следствием 2 и замечанием относительно нестандартных предикатов доказуемости, приведенным выше.

Следствие 3. Для всех $n,m \in \mathbb{N}$, если $n > m \geqslant 1$, то не существует эпиморфизма из $({{\mathfrak{L}}_{T}},\square _{T}^{{(n)}})$ на $({{\mathfrak{L}}_{T}},\square _{T}^{{(m)}})$.

Доказательство.   В   силу   доказуемой ${{\Sigma }_{1}}$-полноты и $m + 1 \leqslant n$, в EA выводимо $\forall \sigma $ ∈ ∈ ${{\Sigma }_{1}}({{\square }^{{((m + 1) \cdot m)}}}\sigma \to \,\square _{T}^{{(m \cdot n)}}\sigma )$, откуда, в силу пункта (iii) следствия 2 при $k = m$ и возможности заменить итерированные  предикаты  доказуемости  на ${\text{EA}}$-эквивалентные стандартные предикаты, вытекает требуемый результат.

В частности, при n = 2, m = 1 мы получаем, что не существует эпиморфизма из алгебры $({{\mathfrak{L}}_{T}},{{\square }_{T}}{{\square }_{T}})$ на алгебру $({{\mathfrak{L}}_{T}},{{\square }_{T}})$, что подтверждает гипотезу из [1].

Хотя достаточное условие Шаврукова из теоремы 1 строго сильнее условия из теоремы 2, оно имеет более теоретико-доказательственную форму, и поэтому более удобно при применении к конкретным парам теорий. Применение условия Адамссона требует более тщательного анализа длины доказательств ${{\Sigma }_{1}}$-предложений в рассматриваемых теориях для получения точных оценок на скорость роста функций ${{\mathcal{R}}_{T}}(x)$ и ${{\mathcal{R}}_{S}}(x)$, но оно также позволяет получить новые примеры неизоморфизма в тех случаях, когда теорема 1 не применима.

Следующая теорема (вместе с пунктом (iii) следствия 2) показывает, что условие Шаврукова может быть существенно ослаблено с сохранением его теоретико-доказательственной формы.

Теорема 4. Если теория $T$ доказывает схему $\mathop {{\text{Rfn}}}\nolimits_{{{\Sigma }_{1}}} (S)$ и этот факт формализуется в виде $T \vdash \forall \sigma \in {{\Sigma }_{1}}{{\square }_{T}}\left( {{{\square }_{S}}\sigma \to \sigma } \right)$, то не существует эпиморфизма из ${{\mathfrak{D}}_{T}}$ на ${{\mathfrak{D}}_{S}}$.

Доказательство. Применяя данное в  формулировке теоремы условие и доказуемую ${{\Sigma }_{1}}$-полноту, получаем $T \vdash \forall \sigma \in {{\Sigma }_{1}}\left( {{{\square }_{S}}{{\square }_{S}}\sigma \to {{\square }_{T}}\sigma } \right)$. Требуемый результат тогда вытекает из пункта (iii) следствия 2 при $k = 1$.

Как следствие доказанной теоремы мы получаем семейство пар теорий с одинаковыми классами доказуемо тотальных вычислимых функций, но неизоморфными алгебрами доказуемости.

Следствие 4. Ни для какого $n \geqslant 1$ не существует эпиморфизма из ${{\mathfrak{D}}_{U}}$ на $({{\mathfrak{L}}_{T}},\square _{T}^{{(n)}})$, где $U$ есть теория $T + \mathop {{\text{Rfn}}}\nolimits_{{{\Sigma }_{1}}} (T)$.

Следующее утверждение дает другой пример подобного рода. Оно вытекает из следствия 4 и теоремы об изоморфизме [9] (с использованием результатов [3, Proposition 5.4] и [2, Corollary 5.2]).

Утверждение 2. Для теорий $U = {\text{E}}{{{\text{A}}}^{ + }}$, $S = U + \mathop {{\text{Rfn}}}\nolimits_{{{\Sigma }_{1}}} (U)$ и $T = U + {\text{RF}}{{{\text{N}}}_{{{{\Sigma }_{1}}}}}(U)$ имеет место 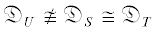, но $\mathcal{F}(U) = \mathcal{F}(S) \ne \mathcal{F}(T)$.

Отметим, что во всех рассмотренных примерах теорий с неизоморфными алгебрами, теории не были доказуемо равнонепротиворечивыми. Следующая теорема дает естественный пример семейства доказуемо ${{\Pi }_{1}}$-эквивалентных (а значит, и равнопротиворечивых) теорий с неизоморфными алгебрами. Напомним, что теория ${{T}_{\omega }}$ есть расширение теории T утверждениями $\neg \,\square _{T}^{{(n)}} \bot $ для всех $n \in \mathbb{N}$. По теореме Горячева теории ${{T}_{\omega }}$ и $T + {\text{Rf}}{{{\text{n}}}_{{{{\Sigma }_{1}}}}}(T)$ являются ${{\Pi }_{1}}$-эквивалентными, и этот факт доказуем в EA (см. [3, Proposition 6.1]).

Теорема 5. Не существует эпиморфизма из ${{\mathfrak{D}}_{U}}$ на ${{\mathfrak{D}}_{{{{T}_{\omega }}}}}$, где $U$ есть теория $T + {\text{Rf}}{{{\text{n}}}_{{{{\Sigma }_{1}}}}}(T)$.

Доказательство. Воспользуемся пунктом (i) следствия 2. В силу утверждения 1 имеем ${{\mathcal{R}}_{{{{T}_{\omega }}}}}(x) \in {{\mathcal{F}}_{{{{T}_{\omega }}}}}({\text{EA}}) = {{\mathcal{F}}_{T}}({\text{EA}})$, где равенство имеет место, поскольку ${{T}_{\omega }}$ есть ${{\Pi }_{1}}$-расширение теории T. Откуда, в силу леммы 1, получаем $\mathcal{R}_{{{{T}_{\omega }}}}^{{(2)}}(x)$ ∈ ∈ $\mathcal{F}_{T}^{2}({\text{EA}})\, \subseteq \,{{\mathcal{F}}_{U}}(U)$, где включение вытекает из доказуемости в EA предложения $\forall \sigma \in {{\Sigma }_{1}}({{\square }_{T}}{{\square }_{T}}\sigma \to \,{{\square }_{U}}\sigma )$.