1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 499, № 1, 2021

Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 499, № 1, стр. 40-43

ОЦЕНКА ЧИСЛА РЕБЕР В ПОДГРАФАХ ГРАФА ДЖОНСОНА

Ф. А. Пушняков 1, А. М. Райгородский 1, 2, 3, 4, *

1 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

2 Московский государственный университет имени М.В. Ломоносова
Москва, Россия

3 Кавказский математический центр Адыгейского государственного университета
Майкоп, Россия

4 Бурятский государственный университет, Институт математики и информатики
Улан-Удэ, Россия

* E-mail: mraigor@yandex.ru

Поступила в редакцию 01.11.2019
После доработки 09.05.2021
Принята к публикации 16.05.2021

Полный текст (PDF)

Аннотация

Получены новые оценки минимального числа ребер в подграфах графа Джонсона.

Ключевые слова: граф Джонсона, дистанционные графы, теорема Турана

Пусть $n > r > s$. Рассмотрим следующее семейство графов:

$\begin{gathered} G(n,r,s) = (V,E),\quad V = \left( {\begin{array}{*{20}{c}} {[n]} \\ r \end{array}} \right), \\ E = \{ (A,B){\kern 1pt} :\;\left| {A \cap B} \right| = s\} , \\ \end{gathered} $
т.е. вершины графа – это всевозможные r-элементные подмножества $[n]: = \{ 1, \ldots ,n\} $, а ребрами мы соединяем пары множеств, пересекающихся ровно по s элементам. Эти графы называются графами Джонсона и играют важную роль в задачах теории кодирования (см. [1]), теории Рамсея (см. [2–4]), комбинаторной геометрии (см. [5–11]), теории гиперграфов (см. [12–19).

Напомним, что независимое множество вершин графа – это любое такое множество его вершин, в котором нет ни одного его ребра, а число независимости графа G – это величина $\alpha (G)$, равная мощности любого из максимальных по числу вершин независимых множеств в G. Классическая проблематика теории графов, восходящая к Турану, состоит в отыскании величины ${{r}_{G}}(l)$, равной минимальному количеству ребер графа G, попадающих внутрь его множества вершин мощности l. Конечно, если $l \leqslant \alpha (G)$, то ${{r}_{G}}(l) = 0$. Поэтому интересны лишь случаи $l > \alpha (G)$.

Классическая теорема Турана утверждает, что на множестве всех графов следующая оценка неулучшаема:

(1)
${{r}_{G}}(l) \geqslant l \cdot \left[ {\frac{l}{{\alpha (G)}}} \right] - \alpha (G) \cdot \frac{{\left[ {\tfrac{l}{{\alpha (G)}}} \right] \cdot \left( {\left[ {\tfrac{l}{{\alpha (G)}}} \right] + 1} \right)}}{2}.$

В частности, если ${{G}_{n}}$ – последовательность графов с растущими к бесконечности числами вершин, а $l = l(n) \to \infty $, $\alpha = \alpha ({{G}_{n}})$ и $\alpha = o(l)$, то

(2)
$\begin{gathered} {{r}_{{{{G}_{n}}}}}(l) \geqslant (1 + o(1))\frac{{{{l}^{2}}}}{{2\alpha }}, \\ \mathop {min}\limits_{\{ {{G}_{n}}\} } {{r}_{{{{G}_{n}}}}}(l) \sim \frac{{{{l}^{2}}}}{{2\alpha }}. \\ \end{gathered} $

Однако для графов $G(n,r,s)$ картина меняется, и именно она интересует нас в этой работе. Во-первых, в серии статей первого автора (см. [6]) подробно исследованы графы ${{G}_{n}} = G(n,3,1)$, для которых, среди прочего, доказано, что в обозначениях и условиях оценки (2)

(3)
$(1 + o(1))\frac{{3{{l}^{2}}}}{{2\alpha }} \leqslant {{r}_{{{{G}_{n}}}}}(l) \leqslant (1 + o(1))\frac{{9{{l}^{2}}}}{{2\alpha }}.$

Иными словами, нижняя оценка в (3) втрое больше оценки (2), которая неулучшаема в общем случае.

Для произвольных графов $G(n,r,s)$ оценок ранее не было. Однако это дистанционные графы, т.е. их вершины можно считать точками в 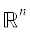(это n-мерные векторы с r единицами и n – r нулями), а ребра тогда – это пары точек на расстоянии $\sqrt {2(r - s)} $. Для графов такого типа в работе [20] доказана следующая оценка. Пусть условия те же, что в неравенстве (2), и, более того, $\alpha n = o(l)$. Тогда

(4)
${{r}_{{{{G}_{n}}}}}(l) \geqslant (1 + o(1))\frac{{{{l}^{2}}}}{\alpha }.$

Таким образом, оценка (4) вдвое сильнее оценки (2).

Прежде всего мы докажем следующую несложную теорему.

Теорема 1. Пусть даны числа r, s. Пусть ${{G}_{n}} = G(n,r,s)$. Пусть $l = l(n) \to \infty $. Тогда

${{r}_{{{{G}_{n}}}}}(l) \leqslant (1 + o(1)) \cdot \frac{{{{l}^{2}}}}{{{{n}^{s}}}} \cdot \frac{{C_{r}^{s} \cdot r!}}{{2 \cdot (r - s)!}}.$

Чтобы сравнить теорему 1 с оценками (1)–(4), надо напомнить, как ведут себя числа независимости графов $G(n,r,s)$. В работе [21] доказана

Теорема 2. Пусть даны числа r, s. Тогда

1. Если $r > 2s + 1$, то при достаточно больших n

$\alpha (G(n,r,s)) = C_{{n - s - 1}}^{{r - s - 1}} \sim \frac{{{{n}^{{r - s - 1}}}}}{{(r - s - 1)!}};$

2. Если $r \leqslant 2s + 1$ и $r - s$ – степень простого числа, то

$\alpha (G(n,r,s)) \sim {{n}^{s}} \cdot \frac{{(2r - 2s - 1)!}}{{r! \cdot (r - s - 1)!}};$

3. Для любых $r,s$ существуют $c(r,s)$ и $d(r,s)$, с которыми

$\begin{gathered} c(r,s) \cdot max\{ {{n}^{s}},{{n}^{{r - s - 1}}}\} \leqslant \alpha (G(n,r,s)) \leqslant \\ \, \leqslant d(r,s) \cdot max\{ {{n}^{s}},{{n}^{{r - s - 1}}}\} . \\ \end{gathered} $

Из теоремы 2 сразу следует, что новая теорема 1 дает лучшую из ранее известных верхних оценок для случая параметров n, 3, 1 – оценку (3). Более того, при $r \leqslant 2s + 1$ получаем, что порядок новой верхней оценки из теоремы 1 совпадает с порядком классических нижних оценок, ведь у них в знаменателе стоит число независимости, которое в данном режиме имеет порядок ns. И только при $r > 2s + 1$ имеется серьезный зазор по порядку. Особенно любопытно выглядит случай с s = 0. Это случай так называемых кнезеровских графов (см. [2]). Получается, что в его рамках новая верхняя оценка из теоремы 1 тривиальна, ибо асимптотически равна $\tfrac{{{{l}^{2}}}}{2}$, а это асимптотика числа ребер полного графа на l вершинах! Как ни странно, это не свидетельство слабости новой оценки. Имеет место

Теорема 3. Пусть ${{G}_{n}} = G(n,r,0)$. Пусть l > > $\alpha (G(n,r,0)) = C_{{n - 1}}^{{r - 1}}$. Тогда

${{r}_{{{{G}_{n}}}}}(l) \geqslant \frac{{l(l - (C_{n}^{r} - C_{{n - r}}^{r}))}}{2}.$

Видно, что если l сильно больше числа независимости, т.е. ${{n}^{{r - 1}}} = o(l)$, то оценка в теореме 3 асимптотически равна $\frac{{{{l}^{2}}}}{2}$. Действительно, разность $C_{n}^{r} - C_{{n - r}}^{r}$ имеет порядок ${{n}^{{r - 1}}}$.

Есть, наконец, интересный режим, в котором теорема 3 не работает. Это режим, когда $l \sim C_{{n - 1}}^{{r - 1}}$. В таком случае оценка теоремы 3 становится отрицательной. Здесь удается доказать следующую теорему.

Теорема 4. Пусть ${{G}_{n}} = G(n,r,0)$. Пусть l > > $\alpha (G(n,r,0)) = C_{{n - 1}}^{{r - 1}}$. Тогда

${{r}_{{{{G}_{n}}}}}(l) \geqslant \mathop {min}\limits_{\beta \leqslant C_{{n - 1}}^{{r - 1}}} \;max\left\{ {l \cdot \left[ {\frac{l}{\beta }} \right] - \beta \cdot \frac{{\left[ {\tfrac{l}{\beta }} \right] \cdot \left( {\left[ {\tfrac{l}{\beta }} \right] + 1} \right)}}{2},(l - \beta )(\beta - {{r}^{2}}C_{{n - 2}}^{{r - 2}})} \right\}.$

Например, если $l = \alpha (G(n,r,0)) + 1$, то все классические оценки принимают значение 1. Однако здесь мы имеем значительное усиление. В самом деле, если $\beta \leqslant 2{{r}^{2}}C_{{n - 2}}^{{r - 2}}$, то первая величина из двух под знаком максимума имеет порядок не ниже nr. При больших β уже вторая величина имеет порядок, как минимум, ${{n}^{{r - 2}}}$. Можно и аккуратнее оценить, но суть ясна и так.

В следующем разделе мы приведем схемы доказательств теорем 1, 3, 4.

СХЕМЫ ДОКАЗАТЕЛЬСТВ

1. Схема доказательства теоремы 1

Рассмотрим множество всех индуцированных подграфов графа $G(n,r,s)$, имеющих l вершин. Для каждого графа H из этого множества и каждого ребра графа $G(n,r,s)$ рассмотрим индикатор вхождения этого ребра в H. Просуммируем индикаторы по всем ребрам и по всем графам двумя способами. С одной стороны, получится произведение числа ребер и числа графов, содержащих данное ребро:

$A = \left( {\frac{1}{2} \cdot C_{n}^{r} \cdot C_{{n - r}}^{{r - s}} \cdot C_{r}^{s}} \right) \cdot \left( {C_{{C_{n}^{r} - 2}}^{{l - 2}}} \right).$

С другой стороны, получится сумма по H чисел ребер в H. Таким образом, минимальное число ребер не меньше, чем

$\frac{A}{{C_{{C_{n}^{r}}}^{l}}} \sim \frac{1}{2} \cdot C_{n}^{r} \cdot C_{n}^{{r - s}} \cdot C_{r}^{s} \cdot \frac{{{{l}^{2}}}}{{{{{(C_{n}^{r})}}^{2}}}} \sim \frac{1}{2} \cdot \frac{{{{l}^{2}}}}{{{{n}^{s}}}} \cdot C_{r}^{s} \cdot \frac{{r!}}{{(r - s)!}}.$

Теорема доказана.

2. Схема доказательства теоремы 3

Пусть W – некоторое множество вершин графа $G(n,r,0)$, имеющее мощность $l$. Тогда для любой вершины $v \in W$ имеем

Суммирование по всем вершинам завершает доказательство.

3. Схема доказательства теоремы 4

Пусть H – подграф графа $G(n,r,0)$, имеющий $l$ вершин. Пусть $\beta $ – максимальная мощность независимого множества вершин в H. Очевидно, $\beta \leqslant \alpha (G(n,r,0)) = C_{{n - 1}}^{{r - 1}}$. Пусть B – любое независимое множество вершин H мощности $\beta $. С одной стороны, имеет место рассуждение, которое восходит к Турану и дает оценку (1) с заменой $\alpha $ на $\beta $. Именно она и стоит первой под знаком максимума. С другой стороны, как и в начале турановского рассуждения, отметим, что каждая вершина H, не принадлежащая $B$, отправляет хотя бы одно ребро в B. Если на этом остановиться, то получится оценка $l - \beta $, которая намного слабее турановской, ибо входит лишь как одно из слагаемых в турановское неравенство. Однако вид второй величины под знаком максимума в теореме 4 подсказывает, что можно значимо усилить утверждение о хотя бы одном ребре, идущем в B. Действительно, покажем, что таких ребер не меньше, чем $\beta - {{r}^{2}}C_{{n - 2}}^{{r - 2}}$. Пусть 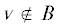, а $w$ – ее гарантированный сосед из B. Пусть $z \in B$ и 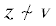. Разумеется, 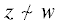, ведь $B$ – независимое множество. Получается, что r-элементные подмножества $R,S$ множества [n], отвечающие вершинам $v,\;w$, не пересекаются (вершины образуют ребро), а $r$-элементное подмножество T, отвечающее z, пересекает и $R$ и $S$. Таких множеств T не больше, чем ${{r}^{2}}C_{{n - 2}}^{{r - 2}}$. Следовательно, не более ${{r}^{2}}C_{{n - 2}}^{{r - 2}}$ вершин из B не соединены с $v$, откуда число вершин в B, являющихся соседками с ${v}$, не меньше $\beta - {{r}^{2}}C_{{n - 2}}^{{r - 2}}$. Теорема доказана.

Список литературы

  1. MacWilliams F.J., Sloane N.J.A. The theory of error-correcting codes. North-Holland, Amsterdam. 1977.

  2. Raigorodskii A.M., Koshelev M.M. New bounds on clique-chromatic numbers of Johnson graphs // Discrete and Applied Math. 2020. V. 283. P. 724–729.

  3. Купавский А.Б., Сагдеев А.А. Теория Рамсея в пространстве с чебышевской метрикой // УМН. 2020. Т. 75. № 5 (455). С. 191–192.

  4. Sagdeev A.A. On the Chromatic Numbers Corresponding to Exponentially Ramsey Sets // J. Math. Sciences. 2020. V. 247. № 3. P. 488–497.

  5. Райгородский А.М. О разбиении множеств на части меньшего диаметра // Доклады РАН. Математика, информатика, процессы управления. 2020. Т. 495. С. 74–77.

  6. Пушняков Ф.А., Райгородский А.М. Оценка числа ребер в особых подграфах некоторого дистанционного графа // Матем. заметки. 2020. Т. 107. № 2. С. 286–298.

  7. Шишунов Е.Д., Райгородский А.М. О числах независимости некоторых дистанционных графов с вершинами в {–1, 0, 1}n // ДАН. 2019. Т. 485. № 3.

  8. Prosanov R. A new proof of the Larman–Rogers upper bound for the chromatic number of the Euclidean space // Discrete Applied Mathematics. 2020. V. 276. P. 115–120.

  9. Просанов Р.И. Контрпримеры к гипотезе Борсука, имеющие большой обхват // Матем. заметки. 2019. Т. 105. № 6. С. 890–898.

  10. Сагдеев А.А. Об одной теореме Франкла–Уилсона // Пробл. передачи информ. 2019. Т. 55. № 4. С. 86–106.

  11. Бердников А.В., Райгородский А.М. Оценки чисел Борсука по дистанционным графам специального вида // Проблемы передачи информации. 2021. Т. 57. № 2. С. 44–50.

  12. Frankl P., Kupavskii A. Almost intersecting families // Electron. J. Comb. 2021. V. 28. № 2. Research Paper P2.7. 16 p.

  13. Frankl P., Kupavskii A. Simple juntas for shifted families // Discrete Anal. 2020. Paper No. 14. 18 p.

  14. Shabanov D.A., Krokhmal N.E., Kravtsov D.A. Panchromatic 3-colorings of random hypergraphs // Europ. J. Combinatorics. 2019. V. 78. P. 28–43.

  15. Cherkashin D., Petrov F. Regular behavior of the maximal hypergraph chromatic number // SIAM J. Discrete Mathematics. 2020. V. 34. № 2. P. 1326–1333.

  16. Райгородский А.М., Черкашин Д.Д. Экстремальные задачи в раскрасках гиперграфов // Успехи матем. наук. 2020. Т. 75. № 1. С. 95–154.

  17. Шабанов Д.А., Шайхеева Т.М. О предписанном хроматическом числе полных многодольных гиперграфов и кратных покрытиях независимыми множествами // Матем. заметки. 2020. Т. 107. № 3. С. 454–465.

  18. Semenov A., Shabanov D. On the weak chromatic number of random hypergraphs // Discrete Applied Mathematics. 2020. V. 276. P. 134–154.

  19. Akhmejanova M.B., Shabanov D.A. Equitable colorings of hypergraphs with few edges // Discrete Applied Mathematics. 2020. V. 276. P. 2–12.

  20. Райгородский А.М., Михайлов К.А. О числах Рамсея для полных дистанционных графов с вершинами в {0, 1}n // Матем. сборник. 2009. Т. 200. № 12. С. 63–80.

  21. Frankl P., Furedi Z. Forbidding just one intersection // J. Combinatorial Theory. Series A. 1985. V. 39. P. 160–176.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал