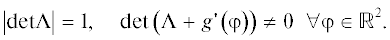Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 500, № 1, стр. 26-30

1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ

История развития гиперболической теории и основные ее достижения подробно описаны в обзоре [1] и монографиях [2, 3]. Одним из аспектов этой теории является вопрос об отыскании конкретных примеров гиперболических динамических систем и связанный с ним вопрос о способах проверки условий гиперболичности. Общепринятым инструментом указанной проверки считается известный критерий конусов [1–3]. Однако к настоящему времени разработан и альтернативный способ обнаружения гиперболического поведения, суть которого состоит в следующем [4, 5].

Пусть M – гладкое риманово многообразие, $A \subset M$ – непустое компактное подмножество, инвариантное относительно диффеоморфизма f, т.е. $f\left( A \right) = A.$ Как и в случае критерия конусов, для проверки факта гиперболичности множества A мы предполагаем существование некоторого стартового разложения касательного пространства ${{T}_{x}}M,$ $x \in A$ в прямую сумму подпространств ${{E}_{1}}\left( x \right),$ ${{E}_{2}}\left( x \right),$ ${\text{dim}}{{E}_{j}}\left( x \right) > 0,$ j = 1, 2. Однако вместо связанных с подпространствами ${{E}_{1}}\left( x \right),$ ${{E}_{2}}\left( x \right)$ полей конусов в нашем случае строятся непосредственно сами неустойчивое и устойчивое распределения $E_{x}^{{\text{u}}},$ $E_{x}^{{\text{s}}},$ фигурирующие в гиперболическом разложении

Как оказывается, искомые подпространства $E_{x}^{{\text{u}}},$ $E_{x}^{{\text{s}}}$ могут быть представлены в параметрической форме

где ${{u}_{1}} \in {{E}_{1}}\left( x \right)$ и ${{u}_{2}} \in {{E}_{2}}\left( x \right)$ – векторные параметры на $E_{x}^{{\text{u}}}$ и $E_{x}^{{\text{s}}}$ соответственно, а линейные операторы $a\left( x \right){\text{:}}\,\,{{E}_{1}}\left( x \right) \to {{E}_{2}}\left( x \right),$ $b\left( x \right){\text{:}}\,\,{{E}_{2}}\left( x \right) \to {{E}_{1}}\left( x \right),$ ограниченные по $x \in A$ в равномерной операторной топологии, подлежат определению. Далее, опираясь на факт Df-инвариантности подпространств (1), (2), для отыскания a(x), b(x) приходим к некоторым нелинейным функциональным уравнениям, к которым, в свою очередь, при определенных дополнительных ограничениях удается применить принцип сжимающих отображений. В результате устанавливаем существование подпространств $E_{x}^{{\text{u}}}$, $E_{x}^{{\text{s}}}$ при $x \in A$ и получаем для них явные параметрические представления (1), (2). После этого, опираясь на указанные представления, отдельно проверяем факты экспоненциального стремления к нулю при $n \to + \infty $ векторов $D({{f}^{n}}(x))\xi $ и $D({{f}^{{ - n}}}(x))\xi ,$ $n \in \mathbb{N}$, при $\xi \in E_{x}^{{\text{s}}}$ и $\xi \in E_{x}^{{\text{u}}}$ соответственно.

Опишем теперь интересующий нас класс диффеоморфизмов. Для этого обозначим через ${{\mathbb{T}}^{2}}$ = = ${{\mathbb{R}}^{2}}{\text{/}}2\pi {{\mathbb{Z}}^{2}}$ тор

Иными словами, ${{\mathbb{T}}^{2}} = p({{\mathbb{R}}^{2}}),$ где p – так называемая естественная проекция. Если отождествить точки тора (3) с точками фундаментальной области

то для p получаем явную формулу

Далее, рассмотрим отображение $G:~{{\mathbb{T}}^{2}} \to {{\mathbb{T}}^{2}},$ имеющее вид

Здесь ${{\Lambda }}$ – невырожденная квадратная матрица размера 2 × 2 с целочисленными элементами, спектр которой не пересекается с единичной окружностью, а вектор-функция $g\left( \varphi \right)$ принадлежит классу ${{C}^{1}}({{\mathbb{R}}^{2}};{{\mathbb{R}}^{2}}).$ Предполагаем также, что она является 2π-периодической по $\varphi \in {{\mathbb{R}}^{2}},$ т.е. $g(\varphi + 2\pi l) \equiv g(\varphi )$ для любого $l \in {{\mathbb{Z}}^{2}}.$ Что же касается элемента Λφ + + $g(\varphi )({\text{mod}}2\pi )$ из ${{\mathbb{T}}^{2}},$ то он задается по правилу:

где $p$ – проекция (4), а через ${{p}^{{ - 1}}}\left( \varphi \right) \in {{\mathbb{R}}^{2}}$ обозначен произвольный прообраз точки $\varphi \in {{\mathbb{T}}^{2}}$ (поскольку разность любых двух таких прообразов есть величина вида $2\pi l,$ где $l \in {{\mathbb{Z}}^{2}},$ то приведенная формула не зависит от конкретного выбора ${{p}^{{ - 1}}}(\varphi )$). И наконец, предполагаем, что (5) – диффеоморфизм тора (3), т.е.

Определим затем понятие гиперболичности применительно к рассматриваемому отображению (5). Для этого нам потребуется линейный оператор $DG(\varphi ):{{\mathbb{R}}^{2}} \to {{\mathbb{R}}^{2}}$ (дифференциал), задающийся равенством $DG(\varphi ) = {{\Lambda }} + g'({{p}^{{ - 1}}}(\varphi ))$ $~\forall ~\varphi \in {{\mathbb{T}}^{2}},$ а также операторы $D({{G}^{n}}\left( \varphi \right)),$ $D({{G}^{{ - n}}}\left( \varphi \right)),$ $n \geqslant 1,$ определяющиеся соотношениями

где ${{\varphi }_{j}} = {{G}^{j}}\left( \varphi \right)$, $j \in \mathbb{Z}.$

О п р е д е л е н и е (У). Будем говорить, что диффеоморфизм (5) г и п е р б о л и ч е с к и й  или является  д и ф ф е о м о р ф и з м о м  А н о с о в а, если для каждого $\varphi \in {{\mathbb{T}}^{2}}$ пространство ${{T}_{\varphi }}{{\mathbb{T}}^{2}} = {{\mathbb{R}}^{2}}$ допускает представление в виде прямой суммы ${{\mathbb{R}}^{2}} = E_{\varphi }^{{\text{u}}} \oplus E_{\varphi }^{{\text{s}}}$ одномерных линейных подпространств $E_{\varphi }^{{\text{u}}},$ $E_{\varphi }^{{\text{s}}}$ и выполняются следующие требования:

а) для $\forall ~\varphi \in {{\mathbb{T}}^{2}}$ имеем $DG(\varphi )E_{\varphi }^{{\text{u}}}\, = \,E_{{G(\varphi )}}^{{\text{u}}},$ $DG(\varphi )E_{\varphi }^{{\text{s}}}$ = = $E_{{G(\varphi )}}^{{\text{s}}}$ (это свойство называется инвариантностью);

б) существуют такие постоянные ${{\mu }_{1}},{{\mu }_{2}} \in \left( {0,1} \right),$ ${{c}_{1}},{{c}_{2}} > 0,$ что

(здесь ||⋅|| – произвольно фиксированная норма в ${{\mathbb{R}}^{2}}$).

Данное определение представляет собой классическое определение Д.В. Аносова из [6]. Следует также напомнить, что в работе [6] гиперболические диффеоморфизмы назывались У-диффеоморфизмами или У-системами. Именно по этой причине мы пометили определение гиперболичности буквой У.

Для описания достаточных условий гиперболичности, которые будут использоваться в данной статье, обозначим через ${{\lambda }_{1}}$, $\left| {{{\lambda }_{1}}} \right| > 1$ и ${{\lambda }_{2}}$, $\left| {{{\lambda }_{2}}} \right| < 1$ собственные значения матрицы ${{\Lambda }}$, а через e₁ и e₂ – отвечающие им собственные векторы. Кроме этого, рассмотрим векторы ${{g}_{s}},s = 1,2,$ удовлетворяющие соотношениям

где Λ* – сопряженная матрица, (⋅, ⋅) – евклидово скалярное произведение в ${{\mathbb{R}}^{2}},$ ${{\delta }_{{js}}}$ – символ Кронекера. Далее, положим

Имеет место следующая

Т е о р е м а 1. При выполнении неравенств

диффеоморфизм (5) обладает свойством гиперболичности.

Доказательство теоремы 1, содержащееся в [4], базируется на описанном выше альтернативном подходе к проверке гиперболичности. А именно, в формулах (1), (2) (в которых теперь $x \in A$ заменено на $\varphi \in {{\mathbb{T}}^{2}}$), мы полагаем ${{E}_{j}}\left( \varphi \right) = {{E}_{j}},$ j = 1, 2, где ${{E}_{j}} = \left\{ {t{{e}_{j}}{\text{:}}~\,t \in \mathbb{R}} \right\},$ j = 1, 2, а ${{e}_{1}},{{e}_{2}}$ – векторы из (7). Один из вариантов достаточных условий гиперболичности, которые удается получить на этом пути, имеет вид (11). Именно он и взят за основу при анализе рассматриваемого ниже класса диффеоморфизмов тора ${{\mathbb{T}}^{2}}.$

2. ОСНОВНОЙ РЕЗУЛЬТАТ

Обратимся сначала к известному линейному отображению “кот Арнольда”, которое в координатах x, y из (3) имеет вид

Далее, введем в рассмотрение отображение

где ${{{{\Delta }}}_{j}}\left( z \right) \in {{C}^{1}}\left( \mathbb{R} \right),$ ${{{{\Delta }}}_{j}}\left( {z + 2\pi } \right) \equiv {{{{\Delta }}}_{j}}\left( z \right),$ j = 1, 2, и выполняются неравенства

Заметим, что условия (14) влекут справедливость второго требования из (6), а значит, обеспечивают взаимную однозначность отображения (13) на торе ${{\mathbb{T}}^{2}}.$ И наконец, следуя идеям работ [7, 8], рассмотрим суперпозицию диффеоморфизмов (12), (13), т.е. отображение

Для формулировки достаточных условий гиперболичности диффеоморфизма (15) нам потребуются некоторые обозначения. А именно, положим

Как оказывается, интересующие нас условия гиперболичности выписываются в терминах постоянных (16)–(19). А именно, справедливо следующее утверждение, являющееся основным результатом данной статьи.

Т е о р е м а 2. Пусть выполнены неравенства

Тогда отображение (15) представляет собой диффеоморфизм Аносова на торе ${{\mathbb{T}}^{2}}.$

Для доказательства заметим, что в случае отображения (15) имеем

а векторы ${{e}_{s}},{{g}_{s}},$ $s = 1,2$ из [7] задаются равенствами

В свою очередь, объединяя соотношения (21) с формулами

где ${{z}_{1}} = 2x + y,{{z}_{2}} = x + y,$ приходим к выводу, что в данной ситуации

Опираясь на базовые соотношения (22)–(25), убеждаемся в том, что здесь

а значит, условия (20) влекут выполнение требований (11). Остается воспользоваться теоремой 1 и заключить, что в предположениях (20) интересующий нас диффеоморфизм (15) действительно является гиперболическим.

В качестве конкретного примера рассмотрим отображение (15) с функциями

Фигурирующие в (26) ограничения на параметры ${{\delta }_{1}},{{\delta }_{2}}$ гарантируют выполнение в данном случае условий (14). Что же касается требований (20), то они эквивалентны оценкам

Заметим еще, что эти условия заведомо справедливы, например, в случае, когда ${{\delta }_{1}} = 0,$ ${{\delta }_{2}} \in \left[ {0,1} \right).$

ЗАКЛЮЧЕНИЕ

Обсудим сначала вопрос о возможных обобщениях полученных нами результатов. Ясно, что при построении класса отображений (15) вместо диффеоморфизма (12) можно взять произвольный линейный гиперболический автоморфизм тора ${{\mathbb{T}}^{2}}.$ Каждому такому автоморфизму будет соответствовать своя версия теоремы 2. Кроме того, даже в первоначальном случае (12), (13) условия указанной теоремы можно несколько ослабить, если для проверки гиперболичности воспользоваться усиленным вариантом теоремы 1.

Для получения более слабых, чем (11) достаточных условий гиперболичности, сначала в формулах (8)–(10) переопределим величины $\beta _{{1,2}}^{0},$ $\beta _{{2,1}}^{0}.$ А именно, положим

Кроме того, введем еще две постоянные

Из результатов статьи [5] вытекает следующая

Т е о р е м а 3. Пусть выполнены условия

где постоянные $\alpha _{1}^{0},\alpha _{2}^{0}$ задаются прежними равенствами (10), а $\beta _{{1,2}}^{0},\beta _{{2,1}}^{0},\gamma _{{1,2}}^{0},\gamma _{{2,1}}^{0}$ – величины (27), (28). Тогда диффеоморфизм (5) является гиперболическим.

Обратим внимание, что в силу очевидной оценки

условия (29) действительно слабее ограничений (11). Однако с использованием теоремы 3 для отображения (15) в общем случае выходят более громоздкие, чем (20) достаточные условия гиперболичности. Именно по этой причине мы изначально остановили свой выбор на теореме 1.

В заключение проиллюстрируем применимость теоремы 3 на конкретном примере, заимствованном из работ [7, 8]. Как и в указанных статьях, рассмотрим диффеоморфизм (15) с функциями

где $M\left( {z,\varepsilon } \right)$ – так называемая функция Мебиуса. Данная функция является 2π-периодической по z и на отрезке $0 \leqslant z \leqslant 2\pi $ задается формулой где $\varepsilon = {\text{const}} \in \left( {0,1} \right),$

Что же касается точек $z = {{z}_{j}},$ $j = 1,2,$ то в них она доопределяется по непрерывности.

Несложный подсчет показывает, что в нашем случае

а значит,

Далее, принимая во внимание приведенные формулы, убеждаемся в том, что в рассматриваемой ситуации условия (29) эквивалентны требованию

Вопрос же о гиперболичности отображения (15), (30) при $\varepsilon \in [1{\text{/}}\sqrt 5 ,1)$ остается открытым.