Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 500, № 1, стр. 52-54

1. В этом сообщении исследуется, в какой мере групповое многообразие алгебраической группы определяет ее групповую структуру. Все рассматриваемые далее алгебраические многообразия считаются определенными над фиксированным алгебраически замкнутым полем k.

Хорошо известно, что в классе связных унипотентных алгебраических групп существует, вообще говоря, бесконечно много зависящих от параметров неизоморфных групповых структур на фиксированном групповом многообразии (которое автоматически изоморфно аффинному пространству).

Более интересным и доступным в отношении исследуемой задачи оказывается класс редуктивных групп. Следующий результат показывает неединственность таких структур в классе связных не полупростых редуктивных алгебраических групп.

Пусть $G$ – связная редуктивная алгебраическая группа, D – ее коммутант, а $Z$ – связная компонента единицы ее центра. Группы D и Z являются соответственно связной полупростой алгебраической группой и тором. Алгебраические группы D × Z и $G$ не всегда изоморфны; существование изоморфизма между ними равносильно равенству $D \cap Z = {\text{\{ }}e{\text{\} }}$, которое, в свою очередь, равносильно тому, что изогения алгебраических групп $D \times Z \to G,(d,z) \mapsto dz$, является их изоморфизмом. Однако, как показывает следующая теорема, D × Z и $G$ всегда изоморфны как алгебраические многообразия.

Теорема 1. Существует такой инъективный гомоморфизм алгебраических групп $\iota {\text{:}}\,Z$ 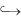$G$, что отображение $\varphi {\text{:}}\,\,D \times Z \to G,(d,z) \mapsto d \cdot \iota (z),$ является изоморфизмом алгебраических многообразий (но, вообще говоря, не гомоморфизмом алгебраических групп).

Следствие 1. Алгебраические группы D × Z и $G$ (в общем случае не являющиеся изоморфными) изоморфны как алгебраические многообразия.

2. Групповые многообразия из теоремы 1 представляются в виде произведений двух многообразий. В теоремах 2–4 найдены ограничения на сомножители таких произведений.

Теорема 2. Алгебраическая кривая не может быть прямым сомножителем многообразия связной полупростой алгебраической группы.

Далее, если не оговорено отдельно, мы считаем, что $k = \mathbb{C}$; топологические термины относятся к классической топологии, а гомологии и когомологии являются сингулярными. По принципу Лефшеца сформулированные ниже теоремы 4, 9, 12, 13 справедливы для любого поля k характеристики нуль.

Теорема 3. Если d-мерное алгебраическое многообразие X является прямым сомножителем многообразия связной редуктивной алгебраической группы, то ${{H}_{d}}(X,\mathbb{Z}) \simeq \mathbb{Z}$ и ${{H}_{i}}(X,\mathbb{Z}) = 0$ при $i > d$.

Следствие 2. Стягиваемое алгебраическое многообразие (в частности, ${{\mathbb{A}}^{d}}$) положительной размерности не может быть прямым сомножителем многообразия связной редуктивной алгебраической группы.

Теорема 4. Алгебраическая поверхность не может быть прямым сомножителем многообразия связной полупростой алгебраической группы.

3. Теорема 1 естественно приводит к вопросу о том, какие геометрические свойства группового многообразия отражаются на алгебраических свойствах соответствующей группы. Явно или неявно этот вопрос давно рассматривался в литературе. Так, М. Лазар доказал в [3], что если многообразие алгебраической группы изоморфно аффинному пространству, то эта группа унипотентна. Ниже приведено несколько результатов по этой теме.

Первый касается так называемых тороидальных групп. По теореме Шевалле, всякая связная алгебраическая группа $G$ содержит наибольшую связную аффинную нормальную подгруппу ${{G}_{{{\text{aff}}}}}$, а группа $G{\text{/}}{{G}_{{{\text{aff}}}}}$ является абелевым многообразием. М. Розенлихт в [4] рассматривал такие группы $G$, названные им тороидальными, что ${{G}_{{{\text{aff}}}}}$ – тор. Теорема 5 дает критерий тороидальности в терминах геометрических свойств алгебраического многообразия $G$ (доказательство не использует ограничений на характеристику поля $k$; ограничение на подмногообразия в теореме 5 является более слабым, чем ограничение, указанное в [2, Prop. 5.4.5 ]):

Теорема 5. Связная алгебраическая группа $G$ тороидальна тогда и только тогда, когда алгебраическое многообразие $G$ не содержит подмного-образий, изоморфных ${{\mathbb{A}}^{1}}$.

Другими результатами по указанной теме являются теорема 6, ее следствие и теорема 7, в которых использованы следующие обозначения. Пусть $X$ – неприводимое алгебраическое многообразие. Мультипликативная группа $k{{[X]}^{ \times }}$ обратимых регулярных функций на X содержит подгруппу ненулевых констант ${{k}^{ \times }}$ и $k{{[X]}^{ \times }}{\text{/}}{{k}^{ \times }}$ является конечно порожденной свободной абелевой группой (см. [4, Thm. 1]). Далее мы полагаем:

Теорема 6. Если $G$ – связная аффинная алгебраическая группа, то размерность ее унипотентного радикала равна $dim(G) - {\text{mh}}(G).$

Следствие 3. Связная аффинная алгебраическая группа G редуктивна тогда и только тогда, когда ${\text{mh}}(G) = dim(G)$.

Предыдущее следствие показывает, что свойство связной аффинной алгебраической группы быть редуктивной выражается через геометрическое свойство ее группового многообразия. Следующая теорема 7, обобщающая теорему М. Лазара [3], показывает, что это же верно и для свойства группы быть разрешимой.

Теорема 7. Следующие свойства связной аффинной алгебраической группы $S$ эквивалентны:

(a) S разрешима;

(б) ${\text{mh}}(S) = {\text{units}}(S)$;

(в) существуют такие неотрицательные целые числа $t$ и r, что алгебраическое многообразие S изоморфно $\mathbb{A}_{ * }^{t} \times {{\mathbb{A}}^{r}}$, где $\mathbb{A}_{ * }^{t}$ – произведение $t$ экземпляров многообразия ${{\mathbb{A}}^{1}}{{\backslash \{ }}0{\text{\} }}$; при этом автоматически $t = {\text{units}}(S)$.

Группа S унипотентна (соответственно, является тором) тогда и только тогда, когда S как алгебраическое многообразие изоморфно ${{\mathbb{A}}^{r}}$ (соответственно, $\mathbb{A}_{ * }^{t}$).

4. Теоремы 8–10 доставляют информацию о множестве всех групповых структур на алгебраическом многообразии, допускающем хотя бы одну такую структуру.

Теорема 8. Две алгебраические группы, одна из которых тороидальна, изоморфны тогда и только тогда, когда они изоморфны как алгебраические многообразия.

Теорема 9. Пусть ${{G}_{1}}$ и ${{G}_{2}}$ – связные аффинные алгебраические группы, а ${{R}_{i}}$ – максимальная редуктивная алгебраическая подгруппа в ${{G}_{i}}$, $i = 1,2$. Если ${{G}_{1}}$ и ${{G}_{2}}$ изоморфны как алгебраические многообразия, то ${{R}_{1}}$ и ${{R}_{2}}$ – связные алгебраические группы с изоморфными алгебрами Ли.

Теорема 10. Пусть $R$ – связная редуктивная алгебраическая группа.

(i) Если $G$ – такая алгебраическая группа, что $G$ и $R$ изоморфны как алгебраические многообразия, то

(a) $G$ связна и редуктивна, а алгебры Ли ${\text{Lie}}(R)$ и ${\text{Lie}}(G)$ изоморфны;

(б) в случае полупростой односвязной группы $R$ алгебраические группы $R$ и $G$ изоморфны.

(ii) Число всех, рассматриваемых с точностью до изоморфизма, алгебраических групп, групповые многообразия которых изоморфны групповому многообразию $R$, конечно.

5. Доказательство утверждения (ii) теоремы 10 использует следующую общую теорему конечности для редуктивных групп, в которой характеристика поля $k$ может быть любой.

Теорема 11. Число всех, рассматриваемых с точностью до изоморфизма, связных редуктивных алгебраических групп фиксированного ранга конечно.

Следствие 4. Число всех, рассматриваемых с точностью до изоморфизма, корневых данных (root data) фиксированного ранга конечно.

Следствие 5. Число всех, рассматриваемых с точностью до изоморфизма, связных компактных групп Ли фиксированного ранга конечно.

6. Если в обозначениях теоремы 1 группа $G$ полупроста (т.е. $Z = {\text{\{ }}e{\text{\} }}$), то эта теорема не доставляет примеров неизоморфных групповых структур на одном и том же групповом многообразии. Такие примеры могут быть получены иным, описанным ниже способом.

Пусть $n$ – целое положительное число, $H$ – односвязная полупростая алгебраическая группа. Группа $G: = H \times \cdots \times H$ ($n$ сомножителей) является связной полупростой, так что ее центр $\mathcal{Z}(G)$ – конечная группа. Пусть ${{F}_{n}}$ – свободная группа ранга $n$ со свободной системой образующих ${{x}_{1}}, \ldots ,{{x}_{n}}$. Для любых элементов $g = ({{h}_{1}}, \ldots ,{{h}_{n}}) \in G$, где ${{h}_{j}} \in H$, и $w \in {{F}_{n}}$ обозначим через $w(g)$ элемент из $H$, являющийся образом элемента w при гомоморфизме ${{F}_{n}} \to H$, который отображает x_j в h_j для каждого j. Любой элемент $\sigma \in {\text{Aut}}({{F}_{n}})$ определяет отображение ${{\sigma }_{G}}{\text{:}}\,\,G \to G$, $g \mapsto (\sigma ({{x}_{1}})(g), \ldots ,\sigma ({{x}_{n}})(g))$, являющееся автоморфизмом группового многообразия $G$ (но, вообще говоря, не группы G). Oграничение ${{\sigma }_{G}}$ на $\mathcal{Z}(G)$ является автоморфизмом группы $\mathcal{Z}(G)$. Рассмотрим какую-либо подгруппу $C$ группы $\mathcal{Z}(G)$.

Теорема 12. (a) Групповые многообразия связных полупростых алгебраических групп G/C и $G{\text{/}}{{\sigma }_{G}}(C)$ изоморфны.

(б) $G{\text{/}}C$ и $G{\text{/}}{{\sigma }_{G}}(C)$ являются изоморфными алгебраическими группами тогда и только тогда, когда C и ${{\sigma }_{G}}(C)$ лежат в одной орбите естественного действия группы ${\text{Out}}(G)$ (изоморфной группе автоморфизмов диаграммы Дынкина группы G) на множестве всех подгрупп группы $\mathcal{Z}(G)$.

С помощью теоремы 12 легко построить примеры неизоморфных связных полупростых алгебраических групп, групповые многообразия которых изоморфны.

Пример. Пусть n = 2, $\sigma ({{x}_{1}}) = {{x}_{1}}$, $\sigma ({{x}_{2}}) = {{x}_{1}}x_{2}^{{ - 1}}$, $H = {\text{S}}{{{\text{L}}}_{d}}$, d ≥ 2, C = ${\text{\{ }}(s,s)|s = {\text{diag}}(\varepsilon , \ldots ,\varepsilon ),{{\varepsilon }^{d}} = 1{\text{\} }}$. В этом случае ${{\sigma }_{G}}(C) = {\text{\{ }}(s,e)|s = {\text{diag}}(\varepsilon , \ldots ,\varepsilon )$, ε^d = 1} не переводится в C группой ${\text{Out}}(G)$. Поэтому $G{\text{/}}C = ({\text{S}}{{{\text{L}}}_{d}} \times {\text{S}}{{{\text{L}}}_{d}}){\text{/}}C$ и $G{\text{/}}{{\sigma }_{G}}(C) = {\text{PS}}{{{\text{L}}}_{d}} \times {\text{S}}{{{\text{L}}}_{d}}$ – неизоморфные связные полупростые алгебраические группы, изоморфные как алгебраические многообразия. Отметим, что если d = 2, то $G = \mathop {{\text{Spin}}}\nolimits_4 $, $G{\text{/}}C = {\text{S}}{{{\text{O}}}_{4}}$.

Аналогично строятся диффеоморфные неизоморфные компактные вещественные группы Ли.

7. Построенные в предыдущем разделе группы полупросты, но не просты. Следующая теорема показывает, что это не случайно.

Теорема 13. Две алгебраические группы, одна из которых связна и проста, изоморфны тогда и только тогда, когда они изоморфны как алгебраические многообразия.

Соображения, использованные в доказательстве теоремы 13, дают и доказательство следующей теоремы, которая в [1] приведена без доказательства.

Теорема 14 [1, Thm. 9.3]. Две связные компактные простые вещественные группы Ли, рассматриваемые как топологические пространства, гомотопически эквивалентны тогда и только тогда, когда они изоморфны как вещественные группы Ли.