Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 500, № 1, стр. 16-22

2.1. Группы с малыми сокращениями

Рассмотрим группу G, заданную образующими и определяющими соотношениями $G = \langle X|\mathcal{R}\rangle $. Мы предполагаем, что множество определяющих соотношений $\mathcal{R}$ замкнуто относительно циклических перестановок и взятия обратных и все элементы из $\mathcal{R}$ являются циклически редуцированными. Взаимодействие между определяющими соотношениями определяется в терминах малых кусков. Слово $s$ называется малым куском по отношению к множеству $\mathcal{R}$ (в обобщенном групповом смысле, см. [ 16, 10]), если существуют соотношения вида $s{{r}_{1}}$ и $s{{r}_{2}}$ в $\mathcal{R}$ такие, что ${{r}_{1}}r_{2}^{{ - 1}} \ne 1$ и ${{r}_{1}}r_{2}^{{ - 1}}$ не сопряжен соотношению из $\mathcal{R}$ в соответствующей свободной группе, даже после сокращений.

Замечание 1. Геометрически малые куски можно рассматривать как слова, которые могут появиться на общей границе между двумя клетками в диаграмме Ван Кампена [13 , 10 ]. В частности, если ${{r}_{1}}r_{2}^{{ - 1}} \in \mathcal{R}$, то мы можем заменить эти клетки одной клеткой. Поэтому с самого начала мы предполагаем, что ${{r}_{1}}r_{2}^{{ - 1}} \notin \mathcal{R}$.

Условие малых сокращений $C(p)$ означает, что каждое соотношение в $\mathcal{R}$ не может быть записано как произведение менее чем $p$ малых кусков. Для большинства целей семи малых кусков достаточно, поскольку при условии C(7) дискретная эйлерова характеристика становится отрицательной [10]. Чтобы гарантировать это, мы можем предположить, что длина любого малого куска меньше одной шестой длины соотношения, в котором он появляется. Основная теорема теории малых сокращений может быть сформулирована так:

Пусть ${{w}_{1}}$, ${{w}_{2}}$ – два слова, которые не содержат вхождений более половины соотношений из $\mathcal{R}$. Они представляют один и тот же элемент из G тогда и только тогда, когда они могут быть соединены однослойной диаграммой [10, Лемма Гриндлингера]. (В частности, группа с малыми сокращениями нетривиальна.) Переход от ${{w}_{1}}$ к ${{w}_{2}}$ может быть представлен в виде последовательности элементарных шагов, называемых поворотами [12]. Каждый поворот поворачивает ровно одну клетку.

Для удобства читателя ниже мы приводим пример однослойной диаграммы, где слово ${{w}_{1}}$ читается на ее верхней стороне, слово ${{w}_{2}}$ – на нижней стороне, а клетки – это групповые соотношения из списка $\mathcal{R}$.

2.2. Основные определения для колец

Пусть $k$ – поле. Мы будем использовать малые греческие буквы для ненулевых элементов поля $k$. Пусть $\mathcal{F}$ – свободная группа, свободно порожденная алфавитом S. Элементы $\mathcal{F}$ называются мономами или словами. Обозначим через $k\mathcal{F}$ групповую алгебру. Элементы $k\mathcal{F}$ называются полиномами. Пусть $a,b \in F$, Через $a \cdot b$ обозначаем их произведение. Мы пишем ab, если между $a$ и $b$ нет сокращений.

Пусть фиксирован конечный или бесконечный набор полиномов $\mathcal{R}$ из $k\mathcal{F}$:

Мы предполагаем, что мономы m_ij являются редуцированными, полиномы ${{p}_{i}}$ – аддитивно редуцированными, $I$ – некоторое множество индексов, все коэффициенты ${{\alpha }_{{ij}}}$ ненулевые.

Обозначим через $\langle \mathcal{R}\rangle $ идеал, порожденный как идеал набором $\mathcal{R}$. Обозначим множество всех мономов ${{m}_{{ij}}}$ из $\mathcal{R}$ через $\mathcal{M}$.

Целью настощей работы является определение класса колец с малыми сокращениями. Такое кольцо мы будем представлять в виде $\mathcal{A} = k\mathcal{F}{\text{/}}\langle \mathcal{R}\rangle $, и наше определение будем формулировать в виде трех условий (аксиом) на $\mathcal{R}$ (набор соотношений) и будем считать $\mathcal{R}$ фиксированными.

Условие 1 (Аксиома совместимости).

(i) Если $p = \sum\limits_{j = 1}^n {{\alpha }_{j}}{{m}_{j}} \in \mathcal{R}$, то $\beta p = \sum\limits_{j = 1}^n \beta {{\alpha }_{j}}{{m}_{j}} \in \mathcal{R}$ для любого $\beta \in k,\beta \ne 0$.

(ii) Пусть $x \in S \cup {{S}^{{ - 1}}}$, где S – алфавит, свободно порождающий $\mathcal{F}$, $p = \sum\limits_{j = 1}^n {{\alpha }_{j}}{{m}_{j}} \in \mathcal{R}$. Предположим, что x^–1 – начальный символ какого-то m_i. Тогда 

(после сокращений в мономах $x{{m}_{j}}$). Мы требуем, чтобы аналогичное условие выполнялось также, если x^–1 – последний символ монома и умножение на x в последнем равенстве – с правой стороны.

Из второго условия аксиомы совместимости немедленно следует, что множество $\mathcal{M}$ замкнуто относительно взятия подслов. В частности, пустое слово всегда принадлежит $\mathcal{M}$.

Определим понятие малого куска относительно $\mathcal{R}$ в алгебре $k\mathcal{F}$. Оно играет центральную роль в нашей теории.

Определение 1. Пусть $c \in \mathcal{M}$. Предположим, существуют два полинома

такие что $c$ является подсловом в $a$ и в $b$, т.е. где ${{\hat {a}}_{1}}$, ${{\hat {a}}_{2}}$, ${{\hat {b}}_{1}}$, ${{\hat {b}}_{2}}$ возможно являются пустыми. Предположим, что (даже после сокращений ), или (даже после сокращений). Тогда моном c называется малым куском.

Обозначим множество всех малых кусков через $\mathcal{S}$. Ясно, что $\mathcal{S} \subseteq \mathcal{M}$. Из определения следует, что множество $\mathcal{S}$ замкнуто относительно взятия подслов. В частности, если множество $\mathcal{S}$ непусто, пустое слово всегда будет малым куском. Если набор $\mathcal{S}$ оказался пустым, то мы все равно полагаем пустое слово малым куском.

Пусть $u \in \mathcal{M}$. Тогда или $u = {{l}_{1}} \cdots {{l}_{m}}$, где ${{l}_{1}}, \ldots ,{{l}_{m}}$ – малые куски, или $u$ не может быть представлено как произведение малых кусков. Введем меру на мономах из $\mathcal{M}$ (Λ-мера). Будем говорить, что $\Lambda (u) = m$, если $u$ может быть представлен как произведение малых кусков и минимальное возможное число малых кусков, в таком представлении равняется $m$. Будем говорить, что $\Lambda (u) = \infty $, если $u$ не может быть представлен как произведение малых кусков.

Зафиксируем константу $\tau \in \mathbb{N}$, $\tau \geqslant 10$.

Условие 2 (Аксиома малых сокращений с условием $\tau $).

Предположим, что ${{p}_{1}}, \ldots ,{{p}_{n}} \in \mathcal{R}$ и линейная комбинация $\sum\limits_{s = 1}^n \,{{\gamma }_{s}}{{p}_{s}}$ является ненулевой после приведения подобных членов.

Тогда существует моном a в $\sum\limits_{s = 1}^n \,{{\gamma }_{s}}{{p}_{s}}$ с ненулевым коэффициентом после приведения подобных членов такой, что:

или $a$ не может быть представлен как произведение малых кусков,

или каждое представление $a$ в качестве произведения малых кусков содержит, по крайней мере, $\tau + 1$ малых кусков.

То есть, $\Lambda (a) \geqslant \tau + 1$, включая $\Lambda (a) = \infty $.

Определение 2. Пусть $p = \sum\limits_{j = 1}^n {{{\alpha }_{j}}} {{a}_{j}} \in \mathcal{R}$. Будем называть мономы ${{a}_{{{{j}_{1}}}}},{{a}_{{{{j}_{2}}}}}$, $1 \leqslant {{j}_{1}},{{j}_{2}} \leqslant n$, инцидентными мономами (включая случай ${{a}_{{{{j}_{1}}}}} = {{a}_{{{{j}_{2}}}}}$). Напомним, что ${{\alpha }_{j}} \ne 0$, $j = 1, \ldots ,n$.

Теперь мы вводим последнее условие, называемое аксиомой изоляции. В отличие от двух предыдущих аксиом, это полностью теоретико-кольцевое условие. В нем мы используем понятие максимального вхождения монома из $\mathcal{M}$ и понятие перекрытия вхождений.

Мы рассматриваем вхождения $a \in \mathcal{M}$ в слово $U$, т.е. $U = LaR$, где $L$, $R$ могут быть пустыми. Под максимальным вхождением мы понимаем вхождение монома из $\mathcal{M}$, которое не содержится в большем таком вхождении. Отметим, что общая часть двух максимальных вхождений всегда является малым куском.

Перекрытие вхождений определяется как общая часть двух вхождений.

Третья аксиома накладывает некоторые естественные ограничения на рассматриваемые кольца. Мы выбрали ее наиболее слабую форму, чтобы охватить наиболее широкий класс колец, что существенно усложнило определение.

Условие 3 (Аксиома изоляции, левая, с условием $\tau $). Пусть ${{m}_{1}},$ ${{m}_{2}},$ $ \ldots ,$ ${{m}_{d}}$ – любая последовательность мономов из $\mathcal{M}$ такая, что ${{m}_{1}} \ne {{m}_{d}}$, $\Lambda ({{m}_{i}}) \geqslant \tau - 2$ для всех $i = 1, \ldots ,d$,

мономы ${{m}_{i}}$ и ${{m}_{{i + 1}}}$ инцидентны для всех $i = 1, \ldots ,d - 1$,

и $a \in \mathcal{M}$ – любой моном со следующими свойствами:

1) $\Lambda (a) \geqslant \tau - 2$;

2) $a{{m}_{1}},a{{m}_{d}} \notin \mathcal{M}$, $a{{m}_{1}}$, $a{{m}_{d}}$ не имеют сокращений;

3) ${{m}_{1}}$ – максимальное вхождение в $a{{m}_{1}}$, ${{m}_{d}}$ – максимальное вхождение в $a{{m}_{d}}$;

4) если $a{{p}_{1}}$ – максимальное вхождение в $a{{m}_{1}}$, которое содержит a, $a{{p}_{d}}$ – максимальное вхождение в $a{{m}_{d}}$, которое содержит a, то существуют мономы l, $l' \in \mathcal{M}$ такие, что

• $l$, $l'$ – малые куски;

• $la,l'a \in \mathcal{M}$, la, $l'a$ не имеют сокращений;

• существует последовательность мономов b₁, ..., ${{b}_{n}}$ из $\mathcal{M}$ таких, что ${{b}_{1}} = la{{p}_{1}}$, ${{b}_{n}} = l'a{{p}_{d}}$, для всех i = 1, ..., $n - 1$ мономы ${{b}_{i}},{{b}_{{i + 1}}}$ инцидентны, и $\Lambda ({{b}_{i}}) \geqslant $ τ – 2.

Тогда $\mathop {{{p}_{1}}}\nolimits^{ - 1} \cdot {{m}_{1}} \ne \mathop {{{p}_{d}}}\nolimits^{ - 1} \cdot {{m}_{d}}$.

Правая аксиома изоляции с условием $\tau $ формулируется симметрично.

Определение 3. Будем говорить, что $\mathcal{A} = k\mathcal{F}{\text{/}}\langle \mathcal{R}\rangle $ есть $C(\tau )$-кольцо с малыми сокращениями, если оно удовлетворяет аксиоме совместимости, аксиоме малых сокращений с условием $\tau $ и по крайней мере одной из аксиом изоляции с условием $\tau $.

Если дана группа $G = \langle X|\mathcal{R}\rangle $ и $m = pq \in \mathcal{R}$, $w = lpr$, тогда преобразование $w = lpr \mapsto l{{q}^{{ - 1}}}r$ = w' называется  поворотом.

Мы заменяем понятие группового поворота понятием кольцевого мультиповорота. Возьмем $\sum\limits_{j = 1}^n {{{\alpha }_{j}}{{m}_{j}}} \, \in \,\mathcal{R}$, где все ${{\alpha }_{j}} \ne 0$. Предположим, что ${v}$ – это моном вида ${v} = l{{m}_{h}}r$ для некоторого $h$, $1 \leqslant h \leqslant n$. Переход от ${v} = l{{m}_{h}}r$ к $\sum\limits_{j = 1,j \ne h}^n ( {\kern 1pt} - {\kern 1pt} \alpha _{h}^{{ - 1}}{{\alpha }_{j}})l{{m}_{j}}r$ называется мультиповоротом. Это преобразование продолжается линейно на $\beta {v}$, а затем линейно на все полиномы, содержащие мономы вида $\beta {v}$. Соответствующий полином $\sum\limits_{j = 1}^n {{{\alpha }_{j}}l{{m}_{j}}r} $ называется раскладкой данного мультиповорота.

Примеры. В данных примерах для простоты рассматривается групповая алгебра над полем из двух элементов.

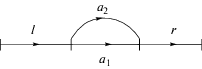
A. Предположим ${v} = l{{a}_{1}}r$ и берется полином ${{a}_{1}} + {{a}_{2}} \in \mathcal{R}$. В этом случае мы получаем переход от $l{{a}_{1}}r$ к $l{{a}_{2}}r$ в результате соответствующего мульти-поворота:

Переход от $l{{a}_{1}}r$ к $l{{a}_{2}}r$ показывает, что поворот можно рассматривать в качестве частного случая мультиповорота.

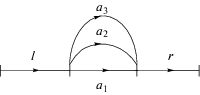
B. Предположим ${v} = l{{a}_{1}}r$ и берется полином ${{a}_{1}} + {{a}_{2}} + {{a}_{3}} \in \mathcal{R}$. Тогда мы получаем переход от $l{{a}_{1}}r$ к $l{{a}_{2}}r + l{{a}_{3}}r$. Графически это выглядит следующим образом:

C. Предположим ${v} = lq{{a}_{1}}{{q}^{{ - 1}}}r$ и берется полином ${{a}_{1}} + {{a}_{2}} + 1 \in \mathcal{R}$. Тогда соответствующий мультиповорот – это переход от $lq{{a}_{1}}{{q}^{{ - 1}}}r$ к $lq{{a}_{2}}{{q}^{{ - 1}}}r$ + l · r. Заметим, что поле замены a₁ на 1, подслово q сокращаетсяс подсловом q^–1. Результат имеет следующий вид (пустое слово 1 не отражено на рисунке):

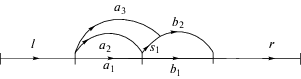
D. Предположим ${v} = l{{a}_{1}}{{b}_{1}}r$ и берутся следующие полиномы ${{a}_{1}} + {{a}_{2}} + {{a}_{3}}s_{1}^{{ - 1}}$ и ${{b}_{1}} + {{b}_{2}} + 1$ из $\mathcal{R}$. Тогда имеются два соседних мультиповорота: a₁ заменяется на ${{a}_{2}} + {{a}_{3}}s_{1}^{{ - 1}}$ и b₁ заменяется на ${{s}_{1}}{{b}_{2}} + 1$.

Предположим, что сначала выполняется мультиповорот слева, а затем мультиповорот справа. Тогда $l{{a}_{1}}{{b}_{1}}r$ заменяется на $l{{a}_{2}}{{b}_{1}}r + l{{a}_{3}}s_{1}^{{ - 1}}{{b}_{1}}r$, а затем результат заменяется на la₂s₁b₂r + la₂ · r + + $l{{a}_{3}}{{b}_{2}}r\, + \,l{{a}_{3}}s_{1}^{{ - 1}}$ · r. При этом в мономах $l{{a}_{2}}r$ и $l{{a}_{3}}s_{1}^{{ - 1}}r$ могут возникнуть сокращения. Теперь предположим, что сначала выполняется мультиповорот справа, а затем мультиповорот слева. Тогда $l{{a}_{1}}{{b}_{1}}r$ заменяется на $l{{a}_{1}}{{s}_{1}}{{b}_{2}}r + l{{a}_{1}} \cdot r$, а затем результат заменяется на $l{{a}_{2}}{{s}_{1}}{{b}_{2}}r + l{{a}_{3}}{{b}_{2}}r + l{{a}_{2}} \cdot r + l{{a}_{3}}s_{1}^{{ - 1}} \cdot r$ и производятся сокращения в необходимых местах. Заметим, что требуется изменить второй мультиповорот, чтобы приметить его. Также заметим, что итоговый результат не зависит от порядка выполнения мультиповоротов.

Данные выше примеры позволяют увидеть, что, в отличие от групп, в кольцах в результате мультиповоротов возникают новые эффекты.

Определим следующее векторное пространство, ассоциированное с данным мономом и набором мультиповоротов. Сначала рассмотрим моном ${v} = l{{m}_{h}}r$ и один мультиповорот, порожденный полиномом $\sum\limits_{j = 1}^n {{{\alpha }_{j}}{{m}_{j}} \in \mathcal{R}} $. Тогда соответствующеепространство линейно порождается мономами $l{{m}_{j}}r,$ $j = 1, \ldots ,n$ (после возможных сокращений) с линейной зависимостью $\sum\limits_{j = 1}^n {{{\alpha }_{j}}l{{m}_{j}}r} $. Теперь рассмотрим моном ${v}$ и несколько мультиповоротов. Тогда соответствующее пространство линейно порождается ${v}$ и всеми мономами, которые получаются из него при помощи данных мультиповоротов, с линейными зависимостями равными раскладкам данных мультиповоротов.

Рассмотрим определенное выше векторное пространство, которое возникает в последнем примере D. В примере D имеются следующие мономы:

и линейные зависимости между ними:

Заметим, что последний полином является суммой предыдущих. Таким образом, у нас имеется 5 линейных зависимостей (а не 6). Следовательно, итоговое векторное пространство имеет размерность не меньше четырех (так как у нас девять попарно различных порождающих мономов). Заметим, что в случае групп соответствующее векторное пространство всегда одномерно, т.е. данный эффект вырождается (см. диаграмму в конце пункта 2.1).