Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 500, № 1, стр. 97-101

СУБРИМАНОВА СФЕРА ЭНГЕЛЯ

Ю. Л. Сачков^1, *, А. Ю. Попов^1, 2

¹ Институт программных систем им. А.К. Айламазяна Российской академии наук
Переславль-Залесский, Ярославская обл., Россия

² Московский центр фундаментальной и прикладной математики
Москва, Россия

^* E-mail: yusachkov@gmail.com

Поступила в редакцию 19.07.2021
После доработки 26.07.2021
Принята к публикации 02.09.2021

DOI: 10.31857/S2686954321050210

Полный текст (PDF)

Аннотация

Описана структура пересечения субримановой сферы на группе Энгеля с двумерным инвариантным множеством дискретных симметрий: регулярность, аналитические свойства, принадлежность exp-$log$-категории, стратификация Уитни, кратность точек, характеризация в смысле анормальных траекторий, сопряженных точек и точек Максвелла, явные выражения субриманова расстояния до особых точек.

Ключевые слова: группа Энгеля, субриманова геометрия, субриманова сфера

Описание метрики Карно–Каратеодори и субримановых сфер является одним из центральных вопросов субримановой геометрии [1, 2]. Известно лишь несколько субримановых геометрий, в которых явно описаны сферы: группа Гейзенберга [3], плоский случай Мартине [4], осесимметричные субримановы структуры на группах SO(3) и SL(2) [6, 5], субримановы структуры на группах SE(2) [7] и SH(2) [8]. Все эти структуры заданы на 3-мерных многообразиях и все, кроме случая Мартине, являются контактными левоинвариантными структурами с вектором роста (2, 3), потому двухступенными. Первое описание трехступенной субримановой структуры – на группе Энгеля – получено в работе [9]. На основе этих результатов, в данной работе мы получаем подробное описание субримановой сферы на группе Энгеля (ее сечения двумерным инвариантным многообразием группы симметрий).

1. ГРУППА ЭНГЕЛЯ

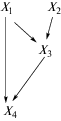
Алгебра Энгеля – это нильпотентная 4-мерная алгебра Ли, в которой существует базис $\mathfrak{g} = {\text{span}}({{X}_{1}}$, ..., X₄), в котором таблица умножения имеет вид

$\begin{gathered} \text{[}{{X}_{1}},{{X}_{2}}] = {{X}_{3}}, \\ [{{X}_{1}},{{X}_{3}}] = {{X}_{4}}, \\ [{{X}_{2}},{{X}_{3}}] = [{{X}_{1}},{{X}_{4}}] = [{{X}_{2}},{{X}_{4}}] = 0. \\ \end{gathered} $

Группа Энгеля G есть связная односвязная группа Ли с алгеброй Ли $\mathfrak{g}$. Ее линейное представление есть

$G = \left\{ {\left( {\begin{array}{*{20}{c}} 1&b&c&d \\ 0&1&a&{{{a}^{2}}{\text{/}}2} \\ 0&0&1&a \\ 0&0&0&1 \end{array}} \right){\text{|}}a,b,c,d \in \mathbb{R}} \right\}.$

Мы будем использовать модель $G \cong \mathbb{R}_{{x,y,z,{v}}}^{4}$, в которой левоинвариантный репер имеет вид

$\begin{gathered} {{X}_{1}} = \frac{\partial }{{\partial x}} - \frac{y}{2}\frac{\partial }{{\partial z}}, \\ {{X}_{2}} = \frac{\partial }{{\partial y}} + \frac{x}{2}\frac{\partial }{{\partial z}} + \frac{{{{x}^{2}} + {{y}^{2}}}}{2}\frac{\partial }{{\partial {v}}}, \\ {{X}_{3}} = \frac{\partial }{{\partial z}} + x\frac{\partial }{{\partial {v}}}, \\ {{X}_{4}} = [{{X}_{1}},{{X}_{3}}] = \frac{\partial }{{\partial {v}}}, \\ \end{gathered} $

как в работе [9]. Наряду с переменной ${v}$, будем использовать переменную $w = {v} - \frac{{{{y}^{3}}}}{6}$.

2. ПОСТАНОВКА И ОСОБЕННОСТИ СУБРИМАНОВОЙ ЗАДАЧИ НА ГРУППЕ ЭНГЕЛЯ

Рассмотрим левоинвариантную субриманову структуру на группе Энгеля G с ортонормированным репером ${{X}_{1}},{{X}_{2}}$:

$\Delta = {\text{span}}({{X}_{1}},{{X}_{2}}),\quad g({{X}_{i}},{{X}_{j}}) = {{\delta }_{{ij}}},\quad i,j = 1,2.$

Выходящие из единицы группы субримановы кратчайшие для этой структуры суть решения задачи оптимального управления

(1)

$\dot {q} = {{u}_{1}}{{X}_{1}} + {{u}_{2}}{{X}_{2}},\quad q \in G,\quad u = ({{u}_{1}},{{u}_{2}}) \in {{\mathbb{R}}^{2}},$

(2)

$q(0) = {\text{Id}},\quad q({{t}_{1}}) = {{q}_{1}},$

(3)

$l = \int\limits_0^{{{t}_{1}}} {\sqrt {u_{1}^{2} + u_{2}^{2}} dt \to min.} $

Эта задача имеет ряд важных особенностей:

– это простейшая субриманова задача глубины 3 (вектор роста (2, 3, 4)),

– это простейшая левоинвариантная субриманова задача с нетривиальными анормальными геодезическими (кратчайшими),

– эта задача проецируется в субриманову задачу в плоском случае Мартине (вектор роста (2, 2, 3)),

– эта задача вкладывается в любую левоинвариантную субриманову задачу с вектором роста больше (2, 3, 4), например, в задачу на группе Картана (вектор роста (2, 3, 5)), задачи с вектором роста $(2,3,5,6)$, $(2,3,5,8)$, $(2,3,4,5)$, ….

3. РАНЕЕ ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

В работе [9], а также в более ранних статьях, цитированных в этой работе, получены следующие результаты для задачи (1)–(3):

– cистема вполне управляема;

– oптимальное управление существует;

– oписаны анормальные траектории:

– это однопараметрические подгруппы ${{e}^{{ \pm t{{X}_{2}}}}}$,

– они проецируются на плоскость $(x,y)$ в прямые,

– поэтому они оптимальны,

– они нестрого анормальны;

– нормальные экстремали удовлетворяют гамильтоновой системе принципа максимума Понтрягина с гамильтонианом H(λ) = = $({{\langle \lambda ,{{X}_{1}}\rangle }^{2}}\, + \,{{\langle \lambda ,{{X}_{2}}\rangle }^{2}}){\text{/}}2$:

(4)

$\dot {\theta } = c,$

(5)

$\dot {c} = - \alpha sin\theta ,$

$\dot {\alpha } = 0,$

$\dot {q} = - sin\theta {{X}_{1}} + cos\theta {{X}_{2}};$

– в фазовом цилиндре уравнения маятника (4), (5) введены координаты $(\varphi ,k)$, в которых это уравнение выпрямляется:

$\dot {\varphi } = \sqrt {{\text{|}}\alpha {\text{|}}} ,\quad \dot {k} = 0;$

– получена параметризация экспоненциального отображения эллиптическими функциями Якоби:

$\begin{gathered} {\text{Exp:}}\,\,C \times {{\mathbb{R}}_{ + }} \to G,\quad {\text{Exp}}(\lambda ,t) = \pi \circ {{e}^{{t\vec {H}}}}(\lambda ) = q(t), \\ C = \,\mathfrak{g}{\text{*}} \cap {{H}^{{ - 1}}}(1{\text{/}}2); \\ \end{gathered} $

– описана дискретная группа симметрий экспоненциального отображения

${{\mathbb{Z}}_{2}} \times {{\mathbb{Z}}_{2}} \times {{\mathbb{Z}}_{2}} = {\text{\{ }}{{\varepsilon }^{i}}{\text{|}}i = 1, \ldots ,8{\text{\} }},$

она порождена отражениями ${{\varepsilon }^{1}}$, ${{\varepsilon }^{2}}$ маятника в осях $\theta $, c и отражением ${{\varepsilon }^{4}}$: $(\theta ,\alpha ) \mapsto (\theta + \pi , - \alpha )$;

– найдены соответствующие времена Максвелла вдоль геодезических;

– доказано, что время разреза есть первое время Максвелла, соответствующее отражениям, получено его явное выражение

${{t}_{{{\text{cut}}}}}:C \to (0, + \infty ];$

– построен оптимальный синтез;

– описано множество разреза.

4. СУБРИМАНОВЫ РАССТОЯНИЕ И СФЕРЫ

Напомним основные определения и свойства субримановой метрики и сфер.

Субриманово расстояние (метрика Карно–Каратеодори) определяется следующим образом:

$d({{q}_{0}},{{q}_{1}}) = inf\left\{ {\int\limits_0^{{{t}_{1}}} {\sqrt {u_{1}^{2} + u_{2}^{2}} dt|\;{\text{управление}}\;({{u}_{1}},{{u}_{2}})(t)\;{\text{переводит}}\;{{q}_{0}}\;{\text{в}}\;{{q}_{1}}} } \right\}.$

Субриманова сфера радиуса R с центром ${{q}_{0}}$ есть

${{S}_{R}}({{q}_{0}}) = {\text{\{ }}q \in G|d({{q}_{0}},q) = R{\text{\} }}.$

В силу инвариантности метрики относительно левых сдвигов на группе Энгеля ${{L}_{q}}{\text{:}}\,\,q{\kern 1pt} ' \mapsto qq{\kern 1pt} '$,

$\begin{aligned} & d(q{{q}_{0}},q{{q}_{1}}) = d({{q}_{0}},{{q}_{1}}), \\ & {{L}_{q}}({{S}_{R}}({{q}_{0}})) = {{S}_{R}}(q{{q}_{0}}). \\ \end{aligned} $

В силу того, что группа Энгеля есть группа Карно, левоинвариантная субриманова структура согласована с дилатациями:

$\begin{gathered} {{\delta }_{\beta }}:(x,y,z,w) \mapsto (\beta x,\beta y,{{\beta }^{2}}z,{{\beta }^{3}}w),\quad \beta > 0, \\ d({\text{Id}},{{\delta }_{\beta }}(q)) = \beta d({\text{Id}},q), \\ {{\delta }_{\beta }}({{S}_{R}}({\text{Id}})) = {{S}_{{\beta R}}}({\text{Id}}). \\ \end{gathered} $

Поэтому достаточно исследовать единичную сферу

$S = {{S}_{1}}({\text{Id}}) = {\text{\{ }}q \in G|d(q,{\text{Id}}) = 1{\text{\} }}.$

Ранее получена параметризация единичной сферы S экспоненциальным отображением:

$S = {\text{\{ Exp}}(\lambda ,1)|\lambda \in C,{{t}_{{{\text{cut}}}}}(\lambda ) \geqslant 1{\text{\} }}.$

Субриманова структура и сфера имеют дискретные симметрии:

${{\varepsilon }^{i}}(S) = S,\quad i = 1, \ldots ,8.$

Основной объект этой работы – сечение сферы двумерным инвариантным многообразием основных симметрий ε¹, ε²:

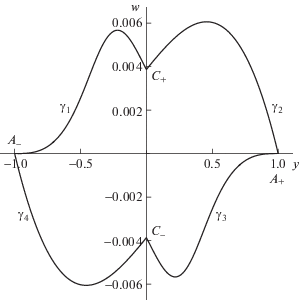
$\tilde {S} = {\text{\{ }}q \in S|{{\varepsilon }^{1}}(q) = {{\varepsilon }^{2}}(q) = q{\text{\} }} = S \cap {\text{\{ }}x = z = 0{\text{\} }}.$

Обозначим подмножества, на которые распадается сечение $\widetilde S$, см. рис. 1:

${{A}_{ \pm }} = \widetilde S \cap {\text{\{ }}w = 0,{\text{sgn}}\,y = \pm 1{\text{\} }},$

${{C}_{ \pm }} = \widetilde S \cap {\text{\{ }}y = 0,{\text{sgn}}\,w = \pm 1{\text{\} ,}}$

${{\gamma }_{1}} = \widetilde S \cap {\text{\{ }}y < 0,w > 0{\text{\} }},$

${{\gamma }_{2}} = \widetilde S \cap {\text{\{ }}y > 0,w > 0{\text{\} ,}}$

${{\gamma }_{3}} = \widetilde S \cap {\text{\{ }}y > 0,w < 0{\text{\} ,}}$

${{\gamma }_{4}} = \widetilde S \cap {\text{\{ }}y < 0,w < 0{\text{\} }},$

(6)

$\widetilde S = {{A}_{ + }} \sqcup {{A}_{ - }} \sqcup {{C}_{ + }} \sqcup {{C}_{ - }} \sqcup ( \sqcup _{{i = 1}}^{4}{{\gamma }_{i}}).$

Рис. 1.

Сечение сферы $\widetilde S$.

Имеются следующие симметрии между этими подмножествами:

$\begin{gathered} {{\varepsilon }^{4}}({{\gamma }_{i}}) = {{\gamma }_{{i + 2}}},\quad i = 1,2, \\ {{\varepsilon }^{4}}({{A}_{ + }}) = {{A}_{ - }},\quad {{\varepsilon }^{4}}({{C}_{ + }}) = {{C}_{ - }}. \\ \end{gathered} $

5. КРАТНОСТЬ ТОЧЕК СЕЧЕНИЯ $\widetilde S$

Кратностью точки $q \in G$ называется величина

$\mu (q) = {\text{card\{ кратчайшие}},\;{\text{соединяющие}}\;{\text{Id}}\;{\text{и}}\;q{\text{\} }}.$

Теорема 1. (1) $\mu ({{A}_{ \pm }}) = 1$.

(2) $\mu ({{C}_{ \pm }}) = \mathfrak{c}$ (континуум $ \cong {{S}^{1}}$).

(3) $q \in {{\gamma }_{i}} \Rightarrow \mu (q) = 2$.

6. ХАРАКТЕРИЗАЦИЯ ТОЧЕК СЕЧЕНИЯ $\widetilde S$

Теорема 2. (1) ${{A}_{ \pm }}$ суть точки на анормальных кратчайших.

(2) ${{C}_{ \pm }}$ суть сопряженные точки, точки Максвелла, точки разреза, центральные элементы группы Энгеля.

(3) $q \in {{\gamma }_{i}}$ суть точки Максвелла, точки разреза.

7. ЯВНЫЕ ВЫРАЖЕНИЯ ДЛЯ СУБРИМАНОВА РАССТОЯНИЯ ДО НЕКОТОРЫХ ТОЧЕК ГРУППЫ ЭНГЕЛЯ

Теорема 3. (1) Если $q(t) = {{e}^{{ \pm t{{X}_{2}}}}}$, $x = z = w$ = 0, $y = \pm t$ есть точка анормальной кратчайшей, то

$d({\text{Id}},q(t)) = t.$

(2) Если $q(t) = {{e}^{{ \pm t{{X}_{4}}}}}$, $x = y = z = 0$, $w = \pm t$ есть центральный элемент группы, то

$\begin{gathered} d({\text{Id}},q(t)) = C\sqrt[3]{t}, \\ C = \sqrt[3]{{48{{K}^{2}}({{k}_{0}})}} \approx 6.37, \\ \quad K({{k}_{0}}) - 2E({{k}_{0}}) = 0,\quad {{k}_{0}} \approx 0.91. \\ \end{gathered} $

8. РЕГУЛЯРНОСТЬ СЕЧЕНИЯ $\widetilde S$

Теорема 4. (1) Кривые ${{\gamma }_{i}}$ аналитичны и регулярны.

(2) ${{A}_{ \pm }}$, ${{C}_{ \pm }}$ суть особые точки, в них $\widetilde S$ негладкая, но липшицева.

(3) ${{\overline \gamma }_{2}} = {{\gamma }_{2}} \cup {\text{\{ }}{{C}_{ + }},{{A}_{ + }}{\text{\} }}$ гладкая класса ${{C}^{\infty }}$.

(4) ${{\gamma }_{1}} \cup {\text{\{ }}{{C}_{ + }}{\text{\} }}$ гладкая класса ${{C}^{\infty }}$.

(5) ${{\gamma }_{1}} \cup {\text{\{ }}{{A}_{ - }}{\text{\} }}$ гладкая класса ${{C}^{1}}$.

9. АНАЛИТИЧЕСКИЕ СВОЙСТВА $\widetilde S$

Множество называется аналитическим, если в некоторой окрестности каждой своей точки оно задается конечной системой вещественно-аналитических уравнений. Множество называется полуаналитическим, если в некоторой окрестности каждой своей точки оно задается конечной системой вещественно-аналитических уравнений и неравенств. Множество называется субаналитическим, если его можно получить из полуаналитических множеств путем конечнократного применения операций объединения, пересечения и взятия образа собственного аналитического отображения. На двумерной плоскости понятия полуаналитических и субаналитических множеств совпадают.

Несубаналитичность субримановых сфер тесно связана с наличием анормальных кратчайших. А.А. Аграчев [11] доказал субаналитичность сфер для субримановых структур без анормальных кратчайших и для многих структур без строго анормальных кратчайших. Позже А.А. Аграчев и А.В. Сарычев [12] показали, что для 2-порождающих субримановых структур (для которых нет анормальных кратчайших) сферы субаналитичны. Известно также, что для плоской субримановой структуры в случае Мартине [4] и для некоторых ее возмущений [13] имеются анормальные кратчайшие, а сферы несубаналитичны.

Теорема 5. (1) Множество $\widetilde S{{\backslash \{ }}{{A}_{ + }},{{A}_{ - }}{\text{\} }}$ полу-аналитично, потому субаналитично.

(2) В окрестности точки ${{A}_{ - }}$ кривая ${{\gamma }_{1}}$ есть график неаналитической функции

$\begin{gathered} w = \frac{1}{6}{{Y}^{3}} - 4{{Y}^{3}}exp\left( { - \frac{2}{Y}} \right)(1 + o(1)), \\ Y = \frac{{y + 1}}{2} \to 0. \\ \end{gathered} $

(3) Поэтому множество $\widetilde S$ неполуаналитично, что эквивалентно несубаналитичности так как $\widetilde S \subset {{\mathbb{R}}^{2}}$.

(4) Следовательно, сфера $S$ несубаналитична.

10. Exp-log-КАТЕГОРИЯ

Функция $f{\text{:}}\,\,{{\mathbb{R}}^{n}} \to \mathbb{R}$ принадлежит exp-log-категории, если она представляется в виде конечной композиции субаналитических функций, экспонент и логарифмов. Множество принадлежит exp-log-категории, если в некоторой окрестности любой своей точки оно является графиком отображения, компоненты которого — функции из exp-log-категории.

Теорема 6. В окрестности точки ${{A}_{ - }}$ кривая ${{\gamma }_{1}}$ есть график функции из exp-log-категории:

$w = F\left( {Y,\,\,\frac{{{{e}^{{ - 1/Y}}}}}{Y}} \right),\quad Y = \frac{{y + 1}}{2} \to 0,$

где $F(\xi ,\eta )$ есть аналитическая функция в окрестности точки $(\xi ,\eta ) = (0,0)$.

Поэтому множество $\widetilde S$ принадлежит exp-log-категории.

11. СТРАТИФИКАЦИЯ УИТНИ

Напомним следующие фундаментальные факты, относящиеся к стратификации Уитни [10]:

если множество субаналитично, то оно является стратифицированным пространством Уитни (С. Лоясевич, Х. Хиронака),

если множество принадлежит exp-log-категории, то оно является стратифицированным пространством Уитни (Ta Lê Loi).

Теорема 7. Разбиение (6) есть стратификация Уитни.

Список литературы

Montgomery R. A tour of subriemannnian geometries, their geodesics and applications. Amer. Math. Soc., 2002.
Agrachev A., Barilari D., Boscain U. A Comprehensive Introduction to sub-Riemannian Geometry from Hamiltonian viewpoint. Cambridge: Cambridge University Press, 2019.
Вершик А.М., Гершкович В.Я. Неголономные динамические системы. Геометрия распределений и вариационные задачи // Итоги науки и техники: Современные проблемы математики. Фундаментальные направления. Т. 16. М.: ВИНИТИ, 1987. С. 5–85.
Agrachev A., Bonnard B., Chyba M., Kupka I. Sub-Riemannian sphere in Martinet flat case // J. ESAIM: Control, Optimisation and Calculus of Variations. 1997. V. 2. P. 377–448.
Берестовский В.Н., Зубарева И.А. Формы сфер специальных неголономных левоинвариантных внутренних метрик на некоторых группах Ли // Сиб. матем. журнал. 2001. Т. 42. № 4. С. 731–748.
Boscain U., Rossi F. Invariant Carnot-Caratheodory metrics on S³, $SO(3)$, $SL(2)$ and Lens Spaces // SIAM Journal on Control and Optimization. 2008. V. 47. P. 1851–1878.
Sachkov Yu.L. Cut locus and optimal synthesis in the sub-Riemannian problem on the group of motions of a plane // ESAIM: COCV. 2011. V. 17. P. 293–321.
Butt Y.A., Sachkov Yu.L., Bhatti A.I. Cut Locus and Optimal Synthesis in Sub-Riemannian Problem on the Lie Group SH(2) // Journal of Dynamical and Control Systems. 2017. V. 23. P. 155–195.
Ardentov A.A., Sachkov Yu. L. Maxwell Strata and Cut Locus in the Sub-Riemannian Problem on the Engel Group // Regular and Chaotic Dynamics. 2017. December. V. 22. Issue 8. P. 909–936.
Горески М., Макферсон Р. Стратифицированная теория Морса. М.: Мир, 1991.
Agrachev A. Compactness for sub-Riemannian length-minimizers and subanalyticity // Rend. Semin. Mat. Torino. 1998. V. 56. P. 1–12.
Agrachev A., Sarychev A. Sub-Riemannian metrics: minimality of abnormal geodesics versus subanalyticity // ESAIM: COCV. 1999. V. 4. P. 377–403.
Bonnard B., Trélat E., On the role of abnormal minimizers in sub-Riemannian geometry // Annales de la faculté des sciences de Toulouse 6^e serie. 2001. V. 10. № 3. P. 405–491.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал