Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 501, № 1, стр. 16-21
О СПЕКТРЕ НЕСАМОСОПРЯЖЕННОГО КВАЗИПЕРИОДИЧЕСКОГО ОПЕРАТОРА
Д. И. Борисов 1, 2, 3, *, А. А. Федотов 4, **
1 Институт математики с вычислительным центром Уфимского федерального исследовательского центра Российской академии наук
Уфа, Россия
2 Башкирский государственный университет
Уфа, Россия
3 Университет Градца Кралове
Градец Кралове, Чешская Республика
4 Санкт-Петербургский государственный университет
Санкт-Петербург, Россия
* E-mail: borisovdi@yandex.ru
** E-mail: a.fedotov@spbu.ru
Поступила в редакцию 30.09.2021
После доработки 18.11.2021
Принята к публикации 18.11.2021
Аннотация
Исследуется оператор $\mathcal{A}$, действующий в ${{l}^{2}}(\mathbb{Z})$ по формуле ${{(\mathcal{A}u)}_{l}} = {{u}_{{l + 1}}} + {{u}_{{l - 1}}} + \lambda {{e}^{{ - 2\pi i(\theta + \omega l)}}}{{u}_{l}}$. Здесь l – целочисленная переменная, а $\lambda > 0$, $\theta \in [0,1)$ и $\omega \in (0,1)$ – параметры. При 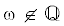 он является простейшим несамосопряженным квазипериодическим оператором. С помощью
перенормировочного подхода описана геометрия его спектра, на спектре вычислен показатель
Ляпунова, описаны условия, при которых спектр является чисто непрерывным либо дополнительно
возникает точечный спектр.
он является простейшим несамосопряженным квазипериодическим оператором. С помощью
перенормировочного подхода описана геометрия его спектра, на спектре вычислен показатель
Ляпунова, описаны условия, при которых спектр является чисто непрерывным либо дополнительно
возникает точечный спектр.
1. ВВЕДЕНИЕ
Здесь мы исследуем спектральные свойства семейства несамосопряженных разностных операторов Шредингера, действующих в ${{l}^{2}}(\mathbb{Z})$ по формуле
(1)
${{({{\mathcal{A}}_{\theta }}u)}_{l}} = {{u}_{{l + 1}}}\, + \,{{u}_{{l - 1}}}\, + \,\lambda {\text{exp}}( - 2\pi i(\theta + \omega l)){{u}_{l}},\,\,\,l \in \mathbb{Z},$Если 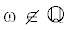 , то функция $l \to {{e}^{{2\pi i(\theta + \omega l)}}}$ – квазипериодическая, и семейство операторов ${{\mathcal{A}}_{\theta }}$ – эргодическое (метрически транзитивное), см. [2]. Квазипериодические операторы возникают в различных задачах современной физики и
привлекают интерес математиков благодаря своим богатым и нетривиальным спектральным
свойствам и широкому кругу математических инструментов и идей, необходимых для их
изучения. Хотя на сегодняшний день накопилось много результатов о спектральных свойствах
самосопряженных квазипериодических дифференциальных и разностных операторов, общая
теория еще далека от завершения. Ее важной лабораторией всегда было и остается изучение
нескольких конкретных моделей, и многие результаты, полученные для них, обобщаются
на широкие классы операторов. Пожалуй, главные и наиболее активно изучаемые модели
– оператор почти-Матье и мэрилендская модель. Они отличаются от оператора ${{\mathcal{A}}_{\theta }}$ заменой в (1) экспоненты на косинус и тангенс соответственно. Их спектральные свойства
существенно зависят от арифметических свойств частоты, величины константы связи и
значений эргодического параметра. Исследование этих операторов началось около 40 лет
назад и активно ведется до сих пор. Среди исследователей – A. Avila, J. Bellissard,
В. Буслаев, B. Helffer, С. Житомирская, И. Качковский, И. Красовский, R. Krikorian,
Y. Last, W. Liu, Л. Парновский, Л. Пастур, J. Puig, B. Simon, Я. Синай, J. Sjöstrand
и многие другие. Имеющаяся литература очень обширна, и мы упомянем лишь две ставшие
классическими книги [1, 2], пару из последних работ [3, 4] и обзор [5], которые помогут заинтересованному читателю войти в проблематику.
, то функция $l \to {{e}^{{2\pi i(\theta + \omega l)}}}$ – квазипериодическая, и семейство операторов ${{\mathcal{A}}_{\theta }}$ – эргодическое (метрически транзитивное), см. [2]. Квазипериодические операторы возникают в различных задачах современной физики и
привлекают интерес математиков благодаря своим богатым и нетривиальным спектральным
свойствам и широкому кругу математических инструментов и идей, необходимых для их
изучения. Хотя на сегодняшний день накопилось много результатов о спектральных свойствах
самосопряженных квазипериодических дифференциальных и разностных операторов, общая
теория еще далека от завершения. Ее важной лабораторией всегда было и остается изучение
нескольких конкретных моделей, и многие результаты, полученные для них, обобщаются
на широкие классы операторов. Пожалуй, главные и наиболее активно изучаемые модели
– оператор почти-Матье и мэрилендская модель. Они отличаются от оператора ${{\mathcal{A}}_{\theta }}$ заменой в (1) экспоненты на косинус и тангенс соответственно. Их спектральные свойства
существенно зависят от арифметических свойств частоты, величины константы связи и
значений эргодического параметра. Исследование этих операторов началось около 40 лет
назад и активно ведется до сих пор. Среди исследователей – A. Avila, J. Bellissard,
В. Буслаев, B. Helffer, С. Житомирская, И. Качковский, И. Красовский, R. Krikorian,
Y. Last, W. Liu, Л. Парновский, Л. Пастур, J. Puig, B. Simon, Я. Синай, J. Sjöstrand
и многие другие. Имеющаяся литература очень обширна, и мы упомянем лишь две ставшие
классическими книги [1, 2], пару из последних работ [3, 4] и обзор [5], которые помогут заинтересованному читателю войти в проблематику.
Оператор ${{\mathcal{A}}_{\theta }}$ введен в [7]. Наш интерес к нему связан с тем, что в его случае очень эффективно работают идеи перенормировочного подхода – метода монодромизации, впервые возникшие в работах Буслаева и Федотова при попытке обобщить теорию Блоха–Флоке на периодические разностные операторы на вещественной оси, см. раздел 5.
Свойства несамосопряженных почти периодических операторов мало изучены, наш подход не зависит от самосопряженности, и нам представляется, что спектральные свойства ${{\mathcal{A}}_{\theta }}$ – нетривиального почти периодического несамосопряженного оператора – допускают весьма полный детальный анализ, а сам оператор может стать важной моделью.
Как для оператора почти-Матье и мэрилендской модели, свойства ${{\mathcal{A}}_{\theta }}$ нетривиально зависят от параметров. Значение $\lambda = 1$ оказывается критическим. Для 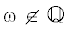 спектр, вещественный при $\lambda \;\leqslant \;1$, становится комплексным при $\lambda > 1$. Физики называют этот эффект $\mathcal{P}\mathcal{T}$-фазовым переходом. Значение $\lambda = 1$ оказывается критическим и для природы спектра. Так, точечный спектр возникает лишь
при $\lambda > 1$ для “достаточно” иррациональных $\omega $.
спектр, вещественный при $\lambda \;\leqslant \;1$, становится комплексным при $\lambda > 1$. Физики называют этот эффект $\mathcal{P}\mathcal{T}$-фазовым переходом. Значение $\lambda = 1$ оказывается критическим и для природы спектра. Так, точечный спектр возникает лишь
при $\lambda > 1$ для “достаточно” иррациональных $\omega $.
В [13] для диофантовых $\omega $ спектр описан как множество и показано, что при $\lambda < 1$ он непрерывен, а при $\lambda > 1$ есть плотный точечный спектр. В [8] результат o геометрии спектра был обобщен на все 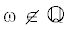 . Мы существенно полнее опишем геометрическую структуру спектра и условия на параметры,
при которых возникают разные типы спектра.
. Мы существенно полнее опишем геометрическую структуру спектра и условия на параметры,
при которых возникают разные типы спектра.
Эта статья – первый шаг нашего исследования. Дальнейшие планы включают, в частности, эффективное описание (обобщенных) собственных функций.
Мы также обсудим разностный оператор Шрёдингера, действующий в ${{L}_{2}}(\mathbb{R})$ по формуле
Легко видеть, что $\mathcal{B}$ может быть разложен прямым интегралом по $\theta $ со слоями ${{\mathcal{A}}_{\theta }}$.
Операторы ${{\mathcal{A}}_{\theta }}$ и $\mathcal{B}$ – ограниченные несамосопряженные операторы. Спектр $\sigma ( \cdot )$ таких операторов вводится как дополнение в комплексной плоскости к резольвентному множеству. Точечный спектр ${{\sigma }_{p}}( \cdot )$ определяется как множество всех собственных значений, а непрерывный спектр ${{\sigma }_{c}}( \cdot )$ – в терминах характеристических последовательностей (последовательностей Вейля). Для остаточного спектра ${{\sigma }_{r}}( \cdot )$ – оставшейся части спектра – справедлива общая формула [9, Гл. 1, § 1]:
(3)
${{\sigma }_{r}}(\mathcal{H}) = \overline {{{\sigma }_{p}}(\mathcal{H}{\kern 1pt} *)} {{\backslash }}{{\sigma }_{p}}(\mathcal{H}),$2. ОБЩИЕ СВОЙСТВА ОПЕРАТОРОВ
Здесь мы обсудим свойства операторов ${{\mathcal{A}}_{\theta }}$ и $\mathcal{B}$, которые нам помогут прокомментировать спектральные результаты. Из свойств прямого интеграла вытекает
Лемма 1. $\sigma (\mathcal{B}) = \bigcup\limits_{\theta \in (0,1)} \sigma ({{\mathcal{A}}_{\theta }})$.
Эта лемма связывает спектры как множества.
На пространстве ${{l}^{2}}(\mathbb{Z})$ зададим линейную и антилинейную инволюции $\mathcal{P}$ и $\mathcal{T}$ по правилам:
Теми же символами, но уже на пространстве ${{L}_{2}}(\mathbb{R})$, обозначим операторы, определенные формулами:
Лемма 2. Справедливы соотношения
С помощью этой леммы легко устанавливаются
Следствие 1. ${{\sigma }_{r}}({{\mathcal{A}}_{\theta }}) = {{\sigma }_{r}}(\mathcal{B}) = \emptyset $ для всех $\theta \in [0,1)$.
Следствие 2. Операторы ${{\mathcal{A}}_{0}}$ и $\mathcal{B}$ являются $\mathcal{P}\mathcal{T}$-симметричными, т.е.
3. ГЕОМЕТРИЯ СПЕКТРА
3.1. Случай иррационального ω
С помощью перенормировочного подхода, сразу для всех 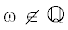 и очень естественно доказывается (см. раздел 5)
и очень естественно доказывается (см. раздел 5)
Теорема 1. Пусть 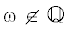 . Тогда спектр (как множество) оператора ${{\mathcal{A}}_{\theta }}$ не зависит от $\theta $. Если при этом $0 < \lambda \;\leqslant \;1$, то спектр – отрезок вещественной оси,
. Тогда спектр (как множество) оператора ${{\mathcal{A}}_{\theta }}$ не зависит от $\theta $. Если при этом $0 < \lambda \;\leqslant \;1$, то спектр – отрезок вещественной оси,
(6)
$\begin{gathered} \sigma ({{\mathcal{A}}_{\theta }}) = \left\{ {E \in \mathbb{C}:\frac{{{{{({\text{Re}}E)}}^{2}}}}{{{\text{c}}{{{\text{h}}}^{2}}\xi }} + \frac{{{{{(\operatorname{Im} E)}}^{2}}}}{{{\text{s}}{{{\text{h}}}^{2}}\xi }} = 4} \right\}, \\ \xi = \ln \lambda . \\ \end{gathered} $Заметим, что совпадение спектров ${{\mathcal{A}}_{\theta }}$ и $\mathcal{B}$ следует из леммы 1 и из того, что спектр ${{\mathcal{A}}_{\theta }}$ не зависит от $\theta $.
То, что спектры либо вещественны, либо симметричны относительно вещественной оси, вытекает из леммы 2.
В условиях теоремы спектр непрерывно зависит от $\lambda $. При $\lambda \to 1 + 0$ эллипс (6) стягивается к отрезку (5).
Наконец, согласно следствию 2, операторы ${{\mathcal{A}}_{0}}$ и $\mathcal{B}$ являются $\mathcal{P}\mathcal{T}$-симметричными. Понятие $\mathcal{P}\mathcal{T}$-симметрии было введено физиками, см., напр., краткий обзор [10]. Если такой оператор зависит от параметра и при его изменении спектр оператора из вещественного превращается в комплексный, то говорят, что происходит $\mathcal{P}\mathcal{T}$-фазовый переход. Мы наблюдаем это явление при $\lambda = 1$.
3.2. Случай рационального $\omega $
Ниже через Arccos мы будем обозначать ветвь арккосинуса, определенную на комплексной плоскости c разрезами вдоль лучей $( - \infty , - 1]$ и $[1,\infty )$ и на их верхних берегах и $[1,\infty )$, аналитическую на разрезанной полуплоскости, отображающая ее на полосу $S = \{ z \in \mathbb{C}: - \pi < {\text{Re}}\,z < 0\} $ и непрерывную вплоть до берегов разрезов.
В этом разделе мы будем иногда указывать зависимость операторa ${{\mathcal{A}}_{\theta }}$ от частоты. Справедлива
Теорема 2. Пусть $\omega = \frac{p}{q}$, где $p,q \in \mathbb{N}$ – взаимно простые числа. Спектр ${{\mathcal{A}}_{\theta }}(p{\text{/}}q)$ описывается формулами
Пусть 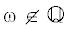 , а $p,q \in \mathbb{N}$ – взаимно простые числа. Для того чтобы величина ${\text{|}}\omega - p{\text{/}}q{\text{|}}$ была достаточно мала, $q$ должно быть достаточно велико. Теорема 2 позволяет детально асимптотически описать
$\sigma ({{\mathcal{A}}_{\theta }}(p{\text{/}}q))$ при $q \to \infty $, но мы ограничимся несколькими замечаниями.
, а $p,q \in \mathbb{N}$ – взаимно простые числа. Для того чтобы величина ${\text{|}}\omega - p{\text{/}}q{\text{|}}$ была достаточно мала, $q$ должно быть достаточно велико. Теорема 2 позволяет детально асимптотически описать
$\sigma ({{\mathcal{A}}_{\theta }}(p{\text{/}}q))$ при $q \to \infty $, но мы ограничимся несколькими замечаниями.
Спектр ${{\mathcal{A}}_{\theta }}(p{\text{/}}q)$ концентрируется около спектра этого оператора с тем же $\lambda $ и иррациональной частотой (по теореме 1 при 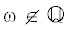 спектр ${{\mathcal{A}}_{\theta }}(\omega )$ от $\omega $ и $\theta $ не зависит). Пусть ${{u}_{\theta }} = \bigcup\limits_{l = 0}^{q - 1} {\left( {{{s}_{\theta }} + \frac{{2\pi l}}{q}} \right)} $.
спектр ${{\mathcal{A}}_{\theta }}(\omega )$ от $\omega $ и $\theta $ не зависит). Пусть ${{u}_{\theta }} = \bigcup\limits_{l = 0}^{q - 1} {\left( {{{s}_{\theta }} + \frac{{2\pi l}}{q}} \right)} $.
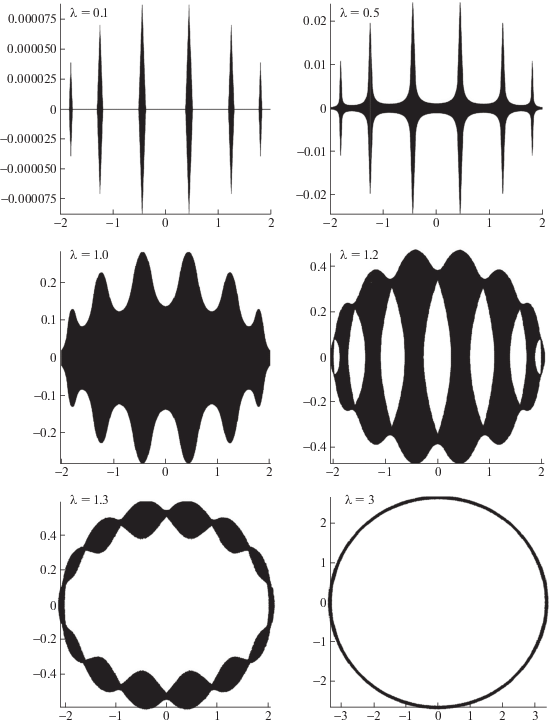
Если $\lambda \;\leqslant \;1$, то множество ${{u}_{\theta }}$ оказывается расположенным в $O({{\lambda }^{{q/2}}}{\text{/}}q)$-окрестности отрезка $[ - \pi ,0]$, который отображение $k \mapsto 2\cos (k)$ переводит в отрезок $[ - 2,2]$ – отрезок из (5). При 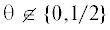 , множество ${{u}_{\theta }}$ состоит из гладких кривых, расположенных в полосах $\frac{1}{q}S + \frac{{2\pi l}}{q}$, $l = 0,1, \ldots ,q - 1$, по одной в полосе. При $\theta \in \left\{ {0,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right\}$ эти кривые становятся частью границ полос.
, множество ${{u}_{\theta }}$ состоит из гладких кривых, расположенных в полосах $\frac{1}{q}S + \frac{{2\pi l}}{q}$, $l = 0,1, \ldots ,q - 1$, по одной в полосе. При $\theta \in \left\{ {0,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right\}$ эти кривые становятся частью границ полос.
Если $\lambda > 1$, то множество ${{u}_{\theta }}$ расположенo в $O({{\lambda }^{{ - q}}}{\text{/}}q)$-окрестностях точек $2\pi \theta + i\ln \lambda + \frac{{2\pi l}}{q}$, l = 0, $1, \ldots ,q - 1$. В каждой из них ${{u}_{\theta }}$ состоит из одного отрезка гладкой кривой. Отображение $k \mapsto 2\cos (k)$ переводит прямую Im$k = \ln \lambda $ в эллипс из (6).
При изменении $\theta $ от нуля до $1{\text{/}}q$ каждая из упомянутых кривых заметает область, симметричную относительно вещественной
оси. Отображение $k \mapsto 2\cos (k)$ переводит объединение этих областей в область, замыкание которой согласно лемме 1
и является спектром оператора $\mathcal{B}(p{\text{/}}q)$. Спектр является одно-, дву- или $(q + 1)$-связным в зависимости от величины ${{\lambda }^{q}}$. Для рациональных и иррациональных $\omega $ спектры оператора $\mathcal{B}$ качественно отличаются: если для 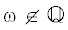 спектр – либо отрезок прямой, либо эллипс, то для $\omega \in \mathbb{Q}$ он является множеством положительной меры на плоскости. Вид этого множества не зависит
от числителя дроби $\omega = p{\text{/}}q$.
спектр – либо отрезок прямой, либо эллипс, то для $\omega \in \mathbb{Q}$ он является множеством положительной меры на плоскости. Вид этого множества не зависит
от числителя дроби $\omega = p{\text{/}}q$.
На рис. 1 мы последовательно (слева направо сверху вниз) изобразили спектры оператора $\mathcal{B}(p{\text{/}}q)$ c $q = 7$ для $\lambda = 0.1,\;0.5,\;1.0,1.2,\;1.3$ и $3.0$. Отметим, каждый из рисунков масштабирован соответствующим образом вдоль вертикальной оси, чтобы продемонстрировать форму спектра.
4. ПРИРОДА СПЕКТРА
Здесь мы сначала обсудим спектр оператора ${{\mathcal{A}}_{\theta }}$, а затем поговорим о спектре $\mathcal{B}$. Для формулировки и обсуждения результатов нам потребуется информация о показателе Ляпунова, играющем важную роль в спектральной теории самосопряженных эргодических операторов.
4.1. Показатель Ляпунова
Сначала, следуя [1, 2], напомним определение и важное свойство показателя Ляпунова. Рассмотрим уравнение
(7)
${{u}_{{l + 1}}} + {{u}_{{l - 1}}} + {v}(\theta + \omega l){{u}_{l}} = E{{u}_{l}},\quad l \in \mathbb{Z},$Перепишем (7) в виде
где(9)
$M(\theta ) = \left( {\begin{array}{*{20}{c}} {E - {v}(\theta )}&{\,\, - 1} \\ 1&0 \end{array}} \right),\quad {{U}_{l}} = \left( {\begin{array}{*{20}{c}} {{{u}_{l}}} \\ {{{u}_{{l - 1}}}} \end{array}} \right).$Для каждого 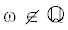 для почти всех $\theta $ предел
для почти всех $\theta $ предел
(10)
$\gamma = \mathop {\lim }\limits_{l \to \infty } \frac{1}{l}\ln \left\| {M(\theta + \omega l) \ldots M(\theta + \omega )M(\theta )} \right\|$Из теории Флоке следует, что предел в (10) существует для рациональных $\omega $, но в этом случае он может зависеть от $\theta $. Мы по-прежнему будем называть этот предел показателем Ляпунова.
Вернемся к оператору ${{\mathcal{A}}_{\theta }}$. Нами доказана
Теорема 3. Для $\omega \in (0,1){{\backslash }}\mathbb{Q}$ показатель Ляпунова $\gamma $ оператора ${{\mathcal{A}}_{\theta }}$ на спектре описывается формулой
При $\omega \in (0,1) \cap \mathbb{Q}$ показатель Ляпунова на спектре равен нулю. Вне спектра $\gamma > 0$ для всех $\omega \in (0,1)$.
Отметим, что формула (11) совпадает с хорошо известной для оператора почти-Матье [5, Теорема 9.1].
4.2. Непрерывный спектр ${{\mathcal{A}}_{\theta }}$ при $0 < \lambda \;\leqslant \;1$
Теорема 4. При $0 < \lambda \;\leqslant \;1$ для всех $\omega \in (0,1)$ и $\theta \in [0,1)$ спектр оператора ${{\mathcal{A}}_{\theta }}$ непрерывен,
Удивительно, но для оператора почти-Матье имеются почти такие же результаты, см. [5, Теоремы 9.1 и 9.5].
Из теорем 3–4 вытекает, что для 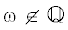 множество нулей показателя Ляпунова состоит только из непрерывного спектра несамосопряженного
оператора ${{\mathcal{A}}_{\theta }}$.
множество нулей показателя Ляпунова состоит только из непрерывного спектра несамосопряженного
оператора ${{\mathcal{A}}_{\theta }}$.
4.3. Точечный спектр ${{\mathcal{A}}_{\theta }}$ при $\lambda > 1$
Пусть 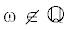 , а $\frac{{{{p}_{k}}}}{{{{q}_{k}}}}$, $k \in \mathbb{N}$, – подходящие дроби цепной дроби, изображающей $\omega $, см. [11]. Положим $\beta (\omega ) = \mathop {\limsup }\limits_{n \to \infty } \frac{{\ln {{q}_{{n + 1}}}}}{{{{q}_{n}}}}$. Чем меньше $\beta (\omega )$, тем хуже число $\omega $ приближается рациональными числами. Ниже $\gamma $ – показатель Ляпунова на спектре ${{\mathcal{A}}_{\theta }}$.
, а $\frac{{{{p}_{k}}}}{{{{q}_{k}}}}$, $k \in \mathbb{N}$, – подходящие дроби цепной дроби, изображающей $\omega $, см. [11]. Положим $\beta (\omega ) = \mathop {\limsup }\limits_{n \to \infty } \frac{{\ln {{q}_{{n + 1}}}}}{{{{q}_{n}}}}$. Чем меньше $\beta (\omega )$, тем хуже число $\omega $ приближается рациональными числами. Ниже $\gamma $ – показатель Ляпунова на спектре ${{\mathcal{A}}_{\theta }}$.
Теорема 5. Пусть $\lambda > 1$. Если $\omega \in \mathbb{Q}$ или $\beta (\omega ) > \gamma $, то спектр оператора ${{\mathcal{A}}_{\theta }}$ чисто непрерывен. Если $\beta (\omega ) < \gamma $, то есть и точечный спектр.
Похожие результаты хорошо известны для оператора почти-Матье и мэрилендской модели [5].
Фактически, случай, когда возникает точечный спектр, изучен нами лучше. Для описания
результатов, считая, что 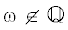 , определим последовательность чисел:
, определим последовательность чисел:
(12)
${{\omega }_{{n + 1}}} = \left\{ {\frac{1}{{{{\omega }_{n}}}}} \right\},\quad n \in \mathbb{N} \cup \{ 0\} ,\quad {{\omega }_{0}} = \omega .$Теорема 6. Пусть $\lambda > 1$, 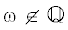 , и выполнено условие
, и выполнено условие
(13)
$\sum\limits_{n = 0}^\infty \frac{1}{{{{\omega }_{{n + 1}}}}}\exp \left( { - \frac{\xi }{{{{\omega }_{0}}{{\omega }_{1}} \ldots {{\omega }_{n}}}}} \right) < \infty ,\quad \xi = \ln \lambda .$Тогда для всех $\theta \in [0,1)$ мы имеем ${{\sigma }_{c}}({{\mathcal{A}}_{\theta }}) = \sigma ({{\mathcal{A}}_{\theta }})$ и
Собственные значения можно описать и формулой
Поэтому все En принадлежат эллипсу (6).
Обсудим условие (13). Прежде всего отметим, что ${{\omega }_{0}}{{\omega }_{1}} \ldots {{\omega }_{{2m - 1}}}\;\leqslant \;{{2}^{{ - m}}}$ для всех $m \in \mathbb{N}$.
Далее, можно показать, что условие (13) гораздо слабее условия $\beta (\omega ) < \gamma (\lambda )$ из теоремы 5. Точнее, при выполнении последнего, ряд в (13) сходится сверхэкспоненциально быстро. С другой стороны, обозначим n-ый член этого ряда через ${{f}_{n}}$. Если ${{\omega }_{0}}{{\omega }_{1}} \ldots {{\omega }_{n}}\ln {\text{|}}{{f}_{{n + 1}}}{\text{|}} \to 0$ при $n \to \infty $, то $\beta (\omega )$ = = γ(λ).
При выполнении условия (13) собственные функции оператора ${{A}_{\theta }}$ можно построить в терминах бесконечного произведения матриц, скорость сходимости которого оказывается не меньше, чем скорость сходимости ряда в (13). Такая конструкция собственных функций для квазипериодических операторов является новой. Мы посвятим ей отдельную работу.
4.4. Спектр оператора $\mathcal{B}$
Теорема 7. Для всех $\lambda > 0$ и $\omega \in (0,1)$ выполнены равенства: ${{\sigma }_{c}}(\mathcal{B}) = \sigma (\mathcal{B})$ и ${{\sigma }_{p}}(\mathcal{B})\, = \,{{\sigma }_{r}}(\mathcal{B})\, = \,\emptyset $.
Аналогичный результат верен и в самосопряженном случае. При этом для 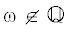 его доказательство использует разложение исследуемого оператора прямым интегралом
и непрерывность плотности состояний для операторов-слоев. Но последняя – объект самосопряженной
теории.
его доказательство использует разложение исследуемого оператора прямым интегралом
и непрерывность плотности состояний для операторов-слоев. Но последняя – объект самосопряженной
теории.
5. КОРОТКО О МЕТОДАХ
Основной метод работы – метод монодромизации – перенормировочный подход, упомянутый во введении. В рамках него возникает бесконечная цепочка квазипериодических разностных уравнений. По решениям любого из них можно построить решения исходного уравнения. Удивительное и нетривиальное свойство уравнения Шрёдингера, соответствующего оператору ${{\mathcal{A}}_{\theta }}$, состоит в том, что все уравнения такой цепочки отличаются от исходного лишь значениями параметров [12]. В частности, для $n$-го уравнения частота равна ${{\omega }_{n}}$ из (12), a константа cвязи равна ${{\lambda }^{{\frac{1}{{{{\omega }_{0}}{{\omega }_{1}} \ldots {{\omega }_{{n - 1}}}}}}}}$. Это и позволяет эффективно описать геометрию спектра, вычислить показатель Ляпунова на спектре и исследовать точечный спектр. Доказательство теоремы 4 использует оригинальный метод. Доказательство второго утверждения теоремы 5 основано на идеях Гордона, Саймона и Житомирской, см., например, [13, 14]. Доказательство теоремы 7 основано на аккуратном анализе пространства решений разностных уравнений на оси с периодическими коэффициентами.
Список литературы
Cycon H.L., Froese R.G., Kirsch W., Simon B. Schrödinger operators with applications to quantum mechanics and global geometry., Berlin: Springer-Verlag, 1987. 329 p.
Pastur L., Figotin A. Spectra of random and almost-periodic operators. Berlin: Springer-Verlag, 1992. 587 p.
Jitomirskaya S., Yang F. // Ergodic Theory Dynam. Systems, in press (2020).
Jitomirskaya S., Konstantinov L., Krasovsky I. // Preprint: arXiv:2007.01005 (2007).
Marx C.A., Jitomirskaya S. // Ergod. Theor. Dynam. Syst. 2017. V. 37. № 8. P. 2353–2393.
Fedotov A. // St. Petersburg Math. J. 2014. V. 25. № 2. P. 303–325.
Sarnak P. // Comm. Math. Phys. 1982. V. 84. No 3. P. 377–401.
Boca F.P. // Duke Math. 2000. J. V. 101. № 3. P. 515–528.
Глазман И.М. Прямые методы качественного спектрального анализа сингулярных дифференциальных операторов. М.: ГИФМЛ, 1963. 339 с.
Bender C.V. // Europhys. News. 2016. V. 47. № 2. P. 17–20.
Хинчин А.Я. Цепные дроби. M.: ГИФМЛ, 1978. 112 с.
Fedotov A. // J. Math. Sci. 2019. V. 238. № 5. 750–761.
Simon B. // Ann. Phys. 1985. V. 159. № 1. P. 157–183.
Jitomirskaya S., Liu W. // Comm. Pure Appl. Math. 2017. V. 70. № 6. P. 1025–1051.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления