Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 501, № 1, стр. 42-45

ДОКАЗАТЕЛЬСТВО УСТОЙЧИВОСТИ В ЗАДАЧЕ БРАУЭРА–ПАУЛЯ

А. П. Иванов^1, 2, *

¹ Математический институт им. В.А. Стеклова Российской академии наук
Москва, Россия

² Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия

^* E-mail: a-p-ivanov@inbox.ru

Поступила в редакцию 16.09.2021
После доработки 16.11.2021
Принята к публикации 17.11.2021

DOI: 10.31857/S2686954321060084

Полный текст (PDF)

Аннотация

Задача об устойчивости равновесия тяжелой частицы в стационарной точке вращающейся поверхности впервые была рассмотрена известным голландским математиком Брауэром в 1918 г. Им было показано, что в случае гладкой поверхности седловая точка, неустойчивая в отсутствие вращения, может быть стабилизирована в некотором диапазоне угловых скоростей. Эта система была рассмотрена Боттема с позиций теории бифуркаций. Физический аналог этой задачи – ионная ловушка Нобелевского лауреата Пауля: здесь вращающаяся твердая опора заменяется квадруполем с периодически меняющимся напряжением, а сила тяжести – электростатическим полем. Условия устойчивости были получены в линейном приближении, а их достаточность до сих пор не доказана. В данной работе такое доказательство проводится методами гамильтоновой механики.

Ключевые слова: шар на вращающемся седле, устойчивость, теория КАМ

1. ВЫВОД ГАМИЛЬТОНИАНА

Будем считать массу частицы единичной, поверхность вращается как твердое тело вокруг фиксированной вертикали $OZ$ с постоянной угловой скоростью $\omega \ne 0$. Свяжем с поверхностью систему координат $OXYZ$ с началом в критической точке. Положение частицы – $x,y$. Пусть $z = f(x,y)$ – уравнение поверхности, тогда для функции Лагранжа имеем выражение

(1)

$\begin{gathered} L = T - gf(x,y), \\ T = \frac{1}{2}({{\left( {\dot {x} - \omega y} \right)}^{2}} + {{\left( {\dot {y} + \omega x} \right)}^{2}} + {{u}^{2}}), \\ u = {{f}_{x}}\dot {x} + {{f}_{y}}\dot {y}, \\ \end{gathered} $

где g – ускорение свободного падения. Выберем единицы измерения длины и времени так, чтобы $\omega = 1,$ $g = 1$. Первый дифференциал функции f в начале координат обращается в нуль, а второй дифференциал считаем невырожденным. Не ограничивая общности, направим оси $OX$ и $OY$ вдоль главных направлений, тогда

(2)

${{d}^{2}}f = \frac{1}{2}(\alpha d{{x}^{2}} + \beta d{{y}^{2}}),\quad \alpha \beta \ne 0.$

Обобщенные импульсы определены формулами

(3)

${{p}_{x}} = \frac{{\partial T}}{{\partial{ \dot {x}}}} = \dot {x} - y + u{{f}_{x}},\quad {{p}_{y}} = \frac{{\partial T}}{{\partial{ \dot {y}}}} = \dot {y} + x + u{{f}_{y}}.$

Функцию Гамильтона строим как преобразование Лежандра лагранжиана (1):

(4)

$\begin{gathered} H = {{p}_{x}}\dot {x} + {{p}_{y}}\dot {y} - L = f(x,y) + \\ \, + {{p}_{x}}({{p}_{x}} + y - \hat {u}{{f}_{x}}) + {{p}_{y}}({{p}_{y}} - x - \hat {u}{{f}_{y}}) - \\ \, - \frac{1}{2}({{\left( {{{p}_{x}} - \hat {u}{{f}_{x}}} \right)}^{2}} + {{\left( {{{p}_{y}} - \hat {u}{{f}_{y}}} \right)}^{2}} + {{{\hat {u}}}^{2}}). \\ \end{gathered} $

Здесь символом $\hat {u}$ обозначена величина $u$, выраженная через канонические переменные.

Для решения вопроса об устойчивости тривиального равновесия системы разложим функцию (4) по формуле Тейлора (величина $\hat {u}$ имеет второй порядок малости):

$H = {{H}_{2}} + {{H}_{3}} + {{H}_{4}} + \ldots ,$

(5)

$\begin{gathered} {{H}_{2}} = \frac{1}{2}(\alpha {{x}^{2}} + \beta {{y}^{2}}) + \frac{1}{2}(p_{x}^{2} + p_{y}^{2}) + {{p}_{x}}y - {{p}_{y}}x, \\ {{H}_{3}} = {{d}^{3}}f, \\ \end{gathered} $

${{H}_{4}} = {{d}^{4}}f - \frac{1}{2}{{\left( {\alpha x({{p}_{x}} + y) + \beta y({{p}_{y}} - x)} \right)}^{2}}.$

2. НЕОБХОДИМЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ

Первый этап – определение необходимых условий устойчивости из анализа формы ${{H}_{2}}$. Для матрицы линеаризованной системы $\dot {\xi }\, = \,A\xi ,$ $\xi \, = \,{{(x,y,{{p}_{x}},{{p}_{y}})}^{T}}$ имеем такое выражение:

(6)

$A = \left( {\begin{array}{*{20}{c}} 0&1&1&0 \\ { - 1}&0&0&1 \\ { - \alpha }&0&0&1 \\ 0&{ - \beta }&1&0 \end{array}} \right).$

Характеристическое уравнение имеет вид

(7)

$\begin{gathered} \det \left( {A - \lambda E} \right) = {{\lambda }^{4}} + (\alpha + \beta + 2){{\lambda }^{2}} + \\ \, + (1 - \alpha )(1 - \beta ) = 0. \\ \end{gathered} $

Корни уравнения (7) чисто мнимы при выполнении системы неравенств

(8)

$\begin{gathered} \alpha {\kern 1pt} \; + \beta {\kern 1pt} \; + 2 > 0,\quad \left( {\alpha {\kern 1pt} \; - 1} \right)\left( {\beta {\kern 1pt} \; - 1} \right) > 0, \\ D = {{\left( {\alpha {\kern 1pt} \; - \beta } \right)}^{2}} + 8(\alpha {\kern 1pt} \; + \beta {\kern 1pt} ) > 0. \\ \end{gathered} $

3. СЛУЧАЙ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА

Допустим, что поверхность имеет второй порядок:

(9)

$f(x,y) = \frac{1}{2}(\alpha {{x}^{2}} + \beta {{y}^{2}}),\quad \alpha < 0,\quad \beta > 0.$

Неравенства (8) выполнены для значений $\beta \in ( - 2$ – α, 1). Данный интервал непуст, если $\alpha > - 3$, что и предполагается ниже. Согласно теории гамильтоновых систем, существует вещественное линейное каноническое преобразование [1–4]:

$L{\text{:}}\,\,(x,y,{{p}_{x}},{{p}_{y}}) \to ({{q}_{1}},{{q}_{2}},{{p}_{1}},{{p}_{2}}),$

приводящее ${{H}_{2}}$ к нормальной форме

(10)

$H_{2}^{*} = \frac{1}{2}{{\omega }_{1}}(q_{1}^{2} + p_{1}^{2}) - \frac{1}{2}{{\omega }_{2}}(q_{2}^{2} + p_{2}^{2}),$

где ${{\omega }_{1}},\;{{\omega }_{2}}$ – мнимые части корней уравнения (7). Различие знаков при слагаемых в формуле (10) обусловлено тем, что при сделанных предположениях форма ${{H}_{2}}$ в формулах (5) знакопеременна.

Важное свойство разложения (5) в рассматриваемом случае: ${{H}_{3}} \equiv 0$, ${{H}_{4}} \leqslant 0$. Это позволяет доказать следующее

Предложение 1. При выполнении условий (8), (9) положение равновесия устойчиво по Ляпунову.

Доказательство. Перейдем от переменных $({{q}_{1}},{{q}_{2}},{{p}_{1}},{{p}_{2}})$ к каноническим полярным координатам $\left( {{{r}_{j}},{{\varphi }_{j}}} \right)$ по формулам

${{q}_{j}} = \sqrt {2{{r}_{j}}} \sin {{\varphi }_{j}},\quad {{p}_{j}} = \sqrt {2{{r}_{j}}} \cos {{\varphi }_{j}},\quad j = 1,2.$

В новых переменных

(11)

$\begin{gathered} H_{2}^{*} = {{\omega }_{1}}r_{1}^{{}} - {{\omega }_{2}}{{r}_{2}},\quad H_{3}^{*} = 0,\quad H_{4}^{*} = - {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }}^{2}}, \\ \hat {u} = \alpha x({{p}_{x}} + y) + \beta y({{p}_{y}} - x), \\ \end{gathered} $

причем старые переменные выражены через новые. Разложим $H_{4}^{*}$:

(12)

$H_{4}^{*} = Q({{r}_{1}},{{r}_{2}}) + F({{r}_{j}},{{\varphi }_{j}}),\quad \int\limits_0^{2\pi } {d{{\varphi }_{1}}\int\limits_0^{2\pi } {Fd{{\varphi }_{2}}} } = 0.$

Функция (12) неположительна при выполнении одного из двух условий: либо $Q({{r}_{1}},{{r}_{2}}) < 0$, либо $Q({{r}_{1}},{{r}_{2}}) \leqslant 0,$ $F \equiv 0$. В первом случае вывод об устойчивости следует из теоремы Арнольда–Мозера [4], так как Q представляет собой нормальную форму в случае отсутствия резонансов до четвертого порядка включительно. Наличие резонанса третьего порядка не влияет на вид этой формы, так как ${{H}_{3}} \equiv 0$. Если же имеет место резонанс четвертого порядка, то устойчивость следует из результатов Маркеева [5].

Во втором случае

$\frac{{\partial H_{4}^{*}}}{{\partial {{\varphi }_{1}}}} = \frac{{\partial H_{4}^{*}}}{{\partial {{\varphi }_{2}}}} \equiv 0,$

откуда ввиду (11) получаем, что функция $\hat {u}$ не зависит от угловых переменных. Допустим, что условие теоремы Арнольда–Мозера о несовместности системы $H_{2}^{*} = 0,$ $Q = 0$ не выполнено. Это означало бы, что $\hat {u}$ пропорционально $H_{2}^{*}$ с некоторым числовым множителем. Такое свойство должно было бы сохраняться и в исходных переменных. Сравнивая выражения для этих функций, заметим, что $\hat {u} = 0$ при $x = y = 0$ и любых $\dot {x},\;\dot {y}$, а величина $H_{2}^{*}$ при этом положительна. Полученное противоречие завершает доказательство.

4. ВЛИЯНИЕ НЕСОВЕРШЕНСТВА ФОРМЫ ПОВЕРХНОСТИ НА УСТОЙЧИВОСТЬ

На практике, построить поверхность, идеально имеющую форму (9), нереально. При этом даже незаметные отклонения в самой функции $f(x,y)$ и ее первом и втором дифференциале могут привести к значительному изменению производных третьего и четвертого порядков. В этом случае источником неустойчивости являются целочисленные соотношения вида

(13)

${{k}_{1}}{{\omega }_{1}} - {{k}_{2}}{{\omega }_{2}} = 0,\quad {{k}_{1}} + {{k}_{2}} \leqslant 4,\quad {{k}_{{1,2}}} \in N.$

Разрешая биквадратное уравнение (7), находим

$\begin{gathered} {{\lambda }^{4}} + (\alpha + \beta + 2){{\lambda }^{2}} + (1 - \alpha )(1 - \beta ) = 0, \\ \lambda _{{1,2}}^{2} = - 1 - \frac{{\alpha + \beta }}{2} \pm \sqrt D , \\ D = {{\left( {\alpha - \beta } \right)}^{2}} + 8\left( {\alpha + \beta } \right). \\ \end{gathered} $

Следовательно,

(14)

$\omega _{1}^{2} = 1 + \frac{{\alpha + \beta }}{2} + \sqrt D ,\quad \omega _{2}^{2} = 1 + \frac{{\alpha + \beta }}{2} - \sqrt D ,$

а) резонанс третьего порядка: $\omega _{1}^{2} = 4\omega _{2}^{2}$. Согласно формулам (14), этот случай реализуется при условии

(15)

$10\sqrt D = 6 + 3\left( {\alpha + \beta } \right).$

Предложение 2. Если ${{d}^{3}}f(x,y) \ne 0$, то для почти всех значений производных третьего порядка функции $f(x,y)$ в нуле и значений параметров, удовлетворяющих равенству (15), положение равновесия неустойчиво.

Данный результат следует из теоремы Маркеева [5].

б) резонанс четвертого порядка: $\omega _{1}^{2} = 9\omega _{2}^{2}$. Этот случай реализуется при условии

(16)

$5\sqrt D = 4 + 2\left( {\alpha + \beta } \right).$

Предложение 3. Если ${{d}^{4}}f(x,y) \ne 0$, то в пространстве значений производных четвертого порядка функции $f(x,y)$ в нуле и значений параметров, удовлетворяющих равенству (16), области устойчивости и неустойчивости имеют ненулевую меру.

Уместность вероятностной формулировки обусловлена наличием погрешностей в форме поверхности $f(x,y)$, не поддающихся строгому учету. Устойчивость имеет место при выполнении некоторого неравенства, связывающего коэффициенты нормальной формы [4], иначе равновесие неустойчиво. Сформулированное утверждение означает, что нет оснований считать один из знаков этого неравенства более вероятным, чем другой.

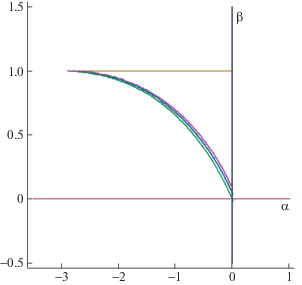
Геометрическая иллюстрация предложений 1–3 приведена на рис. 1. Область (8) – криволинейный треугольник, ограниченный нижней кривой. Выше границы располагаются линии резонансов третьего и четвертого порядков (перечислены снизу вверх).

Рис. 1.

Область устойчивости частицы.

Предложение 4. Если в области устойчивости в первом приближении (8) не выполнено ни одно из равенств (15) или (16), то в пространстве значений производных третьего и четвертого порядка функции $f(x,y)$ в нуле область неустойчивости имеет нулевую меру.

Данный вывод следует из вышеупомянутой теоремы Арнольда–Мозера.

5. СЛУЧАЙ ШАРИКА НЕНУЛЕВОГО РАДИУСА

Заменим в постановке задачи частицу шариком малого радиуса $\rho > 0$. В отсутствие трения реакция не создает момента относительно центра тела, поэтому его угловая скорость не изменяется со временем. Для решения вопроса об устойчивости можно воспользоваться полученными выше результатами, но с существенной поправкой: если точка контакта лежит на поверхности $z = f(x,y)$, то его центр движется по эквидистанте. Для построения последней необходимо в каждой точке исходной поверхности построить нормаль $\gamma $ (с ориентацией вверх) и отложить вдоль нее отрезок, равный радиусу $\rho $. Для координат центра шара $(x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} ')$ имеем выражение

(17)

$(x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} ') = (x,y,z) + \rho \frac{{\left( { - {{f}_{x}}, - {{f}_{y}},1} \right)}}{{\sqrt {f_{x}^{2} + f_{y}^{2} + 1} }}.$

Формула (17) неявно задает уравнение эквидистанты $z{\kern 1pt} ' = g(x{\kern 1pt} ',y{\kern 1pt} ')$. Задача о движении шарика динамически эквивалентна задаче о движении частицы той же массы по этой поверхности. Будем считать, что опора является параболоидом (9) и найдем первые члены разложения функции g.

Поскольку

$\begin{gathered} (x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} ') = (x,y,z) + \rho \frac{{\left( { - \alpha x, - \beta y,1} \right)}}{{\sqrt {1 + \delta } }} = \\ = \,\,(x,y,z) + \rho \left( { - \alpha x, - \beta y,1} \right)\left( {1 - \frac{1}{2}\delta + \frac{3}{8}{{\delta }^{2}} - \ldots } \right), \\ \delta = {{\left( {\alpha x} \right)}^{2}} + {{\left( {\beta y} \right)}^{2}}, \\ \end{gathered} $

то имеем

(18)

$\begin{gathered} x{\kern 1pt} ' = (1 - \alpha \rho )x + \frac{1}{2}\alpha \delta \rho x + \ldots , \\ y{\kern 1pt} ' = (1 - \beta \rho )y + \frac{1}{2}\beta \delta \rho y + \ldots , \\ z{\kern 1pt} ' = \rho + z + \rho \left( { - \frac{1}{2}\delta + \frac{3}{8}{{\delta }^{2}} - \ldots } \right). \\ \end{gathered} $

Следовательно, эквидистанта не имеет особых точек при условии $\beta \rho < 1$, которое ограничивает радиус шарика в данном анализе (напомним, что в рассматриваемом случае $\alpha < 0$). Разрешая соотношения (18) относительно $x,\;y$, получим уравнение для поверхности, по которой движется центр, в виде

$x = \frac{{x{\kern 1pt} '}}{{\left( {1 - \alpha \rho } \right)}}\left( {1 - \frac{{\alpha {\kern 1pt} '\rho \delta {\kern 1pt} '}}{2}} \right) + \ldots ,$

(19)

$\begin{gathered} y = \frac{{y{\kern 1pt} '}}{{\left( {1 - \beta \rho } \right)}}\left( {1 - \frac{{\beta {\kern 1pt} '\rho \delta {\kern 1pt} '}}{2}} \right) + \ldots , \\ {{g}_{2}} = \frac{1}{2}(\alpha {\kern 1pt} 'x{\kern 1pt} {{'}^{2}}\; + \beta {\kern 1pt} 'y{\kern 1pt} {{'}^{2}}),\quad {{g}_{4}} = \frac{1}{8}\rho {{\left( {\delta {\kern 1pt} '} \right)}^{2}}, \\ \delta {\kern 1pt} ' = {{\left( {\alpha {\kern 1pt} 'x{\kern 1pt} '} \right)}^{2}} + {{\left( {\beta {\kern 1pt} 'y{\kern 1pt} '} \right)}^{2}}, \\ \end{gathered} $

$\alpha {\kern 1pt} ' = \frac{\alpha }{{1 - \alpha \rho }},\quad \beta {\kern 1pt} ' = \frac{\beta }{{1 - \beta \rho }}.$

При сделанных оговорках начало координат является седловой точкой для эквидистанты, но, в отличие от случая точечной массы, в ее степенном разложении имеются члены четвертого порядка. Поэтому в разложении (5) функция ${{H}_{4}}$ знакопеременна. Необходимые условия устойчивости выражаются неравенствами (8), где вместо $\alpha ,\beta $ нужно подставить $\alpha ',\beta '$ по формулам (19). Геометрически область устойчивости подвергается дробно-линейному преобразованию: если считать, что на фигуре она изображена в переменных $\alpha ',\beta '$, то для перехода к исходным переменным, описывающим форму опорного параболоида, ее следует растянуть по оси абсцисс и сжать по оси ординат.

Для вывода об устойчивости используется предложение 4.

Список литературы

Brouwer L.E.J. The motion of a particle on the bottom of a rotating vessel under the influence of the gravitational force / in: H. Freudenthal (ed.). Collected Works. II. North-Holland, Amsterdam, 1975. P. 665–686.
Bottema O. Stability of equilibrium of a heavy particle on a rotating surface // ZAMP Z. angew. Math. Phys. 1976. V. 27. P. 663–669.
Пауль В. Электромагнитные ловушки для заряженных и нейтральных частиц // УФН. 1990. Т. 160. Вып. 12.
Arnol’d V.I. Mathematical Methods of Classical Mechanics. Springer, 1978.
Markeev A.P. Stability of a canonical system with two degrees of freedom in the presence of resonance // Appl. Math. Mech. 1969. V. 32. P. 766–772.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал