1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 501, № 1, 2021

Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 501, № 1, стр. 67-73

ГИБРИДНЫЕ СЕТОЧНО-ХАРАКТЕРИСТИЧЕСКИЕ СХЕМЫ ДЛЯ ЗАДАЧ АРКТИЧЕСКОЙ СЕЙСМОРАЗВЕДКИ

Член-корреспондент РАН И. Б. Петров 1, *, В. И. Голубев 1, **, Е. К. Гусева 1

1 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

* E-mail: petrov@mipt.ru
** E-mail: w.golubev@mail.ru

Поступила в редакцию 29.07.2021
После доработки 06.10.2021
Принята к публикации 19.10.2021

Полный текст (PDF)

Аннотация

В настоящей работе рассматривается процесс проведения сейсмической разведки газовых месторождений с установкой источника на поверхности ледового острова. Построена модель, включающая в себя ледовое образование, акваторию, многослойный геологический массив и резервуар с метаном. Для корректного описания динамического поведения отдельных сред использованы уравнения линейной теории упругости, акустики, вязкоупругая модель Максвелла и упруговязкопластическая модель Кукуджанова. Для численного решения определяющей системы уравнений используется сеточно-характеристический метод на прямоугольных расчетных сетках. Между средами в явном виде ставятся физические контактные условия. На основе сеточно-характеристического критерия монотонности построена новая гибридная схема повышенного порядка точности. С ее помощью получено полноволновое решение сейсмической задачи в двумерной постановке.

Ключевые слова: прямая задача сейсморазведки, ледовый остров, математическое моделирование, сеточно-характеристический метод, критерий монотонности, гибридная схема

ВВЕДЕНИЕ

Среди актуальных задач описания природных и индустриальных процессов в Арктическом регионе одной из важнейших является задача об искусственном ледовом острове, который может использоваться в качестве морской платформы. Практическая реализация данной технологии была успешно произведена в Канаде [1, 2]. Комплекс задач, связанный с данной постановкой, был частично рассмотрен в работе [3]. Средой, представляющей наибольший интерес в Арктических задачах, является лед. Он является неоднородным материалом со сложной реологией, некоторые свойства которой изложены в [4]. На практике часто динамическое поведение льда моделируется уравнениями упругости. Например, в работах [5–7] авторами был численно решен ряд задач, включающих различные среды: ледовое поле, морская вода и грунт. Для описания их поведения использовались модели линейной упругости и акустики [8–11].

В настоящей работе рассматривается процесс распространения сейсмических волн в сложно построенной модели, включающей в себя ледовый остров, окружающее его ледовое поле, воду и неоднородный геологический массив. Для учета нелинейного поведения льда используется модель вязкоупругости Максвелла [12, 13] и модель упруговязкопластичности Кукуджанова [14].

Для численного решения определяющей системы уравнений в настоящей работе используется сеточно-характеристический метод [15, 16] на прямоугольных сетках. В задачах о распространении волн в сплошных средах могут возникать большие градиенты искомых функций, поэтому для расчетных схем важно свойство монотонности. Однако монотонных линейных схем с порядком выше первого для гиперболических задач не существует. Для преодоления данной проблемы исследователями было предложено множество подходов, например, использование различных ограничителей потоков таких, как minmod, свойства которого изучались в [17], использование реконструированных значений на границах разрыва, как в ENO- и WENO-схемах [18], использование различных критериев монотонности, например монотонности по Хартену для TVD-схем в [19] и гибридизация [20]. В настоящей работе на основе сеточно-характеристического критерия монотонности [21] была построена новая схема повышенного порядка точности. С ее помощью было получено численное решение задачи ледовой сейсморазведки – обнаружение метанового резервуара в слоистом геологическом массиве.

ПОСТАНОВКА ЗАДАЧИ

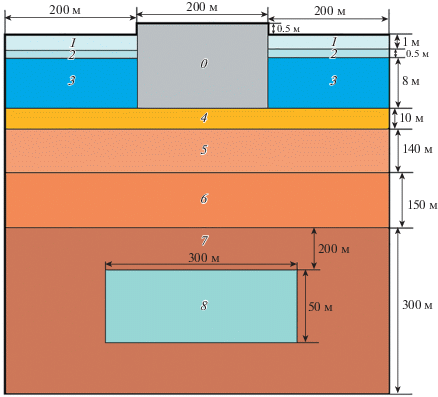
В настоящей работе рассматривается задача о распространении сейсмических волн, инициируемых на поверхности ледового острова. Общий вид расчетной области представлен на рис. 1. Компьютерная модель состоит из следующих физических объектов: 0 – ледовый остров; 1 и 2 – ледовое поле; 3 – толща воды; 4 – осадочные породы; 5–7 – слоистый геологический массив; 8 – резервуар с метаном. Для корректного описания динамических процессов, происходящих в них, каждая из подобластей описывается соответствующей механико-математической моделью: 0 и 1 – модель Максвелла; 2 – модель Кукуджанова; 3 и 8 – уравнения акустики, 4–7 – уравнения линейной изотропной упругости. Между контактирующими средами ставится физически корректное контактное условие полного слипания, а на верхней границе используется условие свободной границы. Использование на нижней и боковых границах условия не отражения позволяет минимизировать численные артефакты от границ расчетной области. Общие размеры модели находятся в пределах 600 м по горизонтальной оси и 610 м по вертикальной оси.

Рис. 1.

Общий вид расчетной области.

В качестве источника сигнала использовалось точечное поверхностное нагружение поверхности льда (области 0) вертикально направленной силой, имеющей синусоидальную зависимость от времени. Целью проводимых расчетов являлось сопоставление волновых полей, формирующихся при наличии резервуара с метаном и в его отсутствии. В табл. 1 указаны параметры всех сред, а также используемых в численных расчетах сеток. Здесь введены обозначения: τ0 – параметр релаксации, k – предел текучести материала, ${{h}_{1}}$ – пространственный шаг сетки по горизонтали, ${{h}_{2}}$ – по вертикали.

Таблица 1.

Параметры сред

Номер слоя ${{c}_{p}},$ м/с ${{c}_{s}},$ м/с $\rho ,$ кг/м3 ${{h}_{1}},$ м ${{h}_{2}}$, м Другие параметры
0 3940 2493 917 0.5 0.1 τ0 = 0.5 с
1 3940 2493 917 1 0.04 τ0 = 0.5 с
2 3940 2493 917 1 0.02 $k = 2.2 \times {{10}^{6}}$ Па, τ0 = 0.5 с
3 1500 – 1000 1 0.4 –
4 1806 316 2000 2 0.2 –
5 1900 800 2000 2 2 –
6 2050 900 2000 2 2 –
7 2250 1000 2000 2 2 –
8 430 – 0.6682 2 1 –

ЧИСЛЕННЫЙ МЕТОД

Рассмотрим определяющую систему уравнений линейной изотропной упругости:

(1)
$\rho {\mathbf{\dot {v}}} = \nabla \cdot \sigma + {\mathbf{f}},$
(2)
$\dot {\sigma } = \lambda \left( {\nabla \cdot {\mathbf{v}}} \right)I + \mu \left( {\nabla \otimes {\mathbf{v}} + {\mathbf{v}} \otimes \nabla } \right),$
где f – вектор внешней силы, $\rho $ – плотность среды, $\sigma $ – тензор напряжений, v – вектор скорости среды, $\lambda $ и $\mu $ – упругие параметры Ламе.

Она является гиперболической, поэтому может быть записана в каноническом виде:

(3)
$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \mathop \sum \limits_{i = 1}^2 {{A}_{i}}\frac{{\partial {\mathbf{u}}}}{{\partial {{x}_{i}}}} = 0,$
где введен вектор неизвестных u = $({{{v}}_{x}},{{{v}}_{y}}$, σxx, ${{\sigma }_{{yy}}},{{\sigma }_{{xy}}}{{)}^{T}}.$

После расщепления системы (3) по пространственным направлениям для численного решения полученных одномерных систем в работе используется сеточно-характеристический метод, основанный на переходе к инвариантам Римана

(4)
${\mathbf{r}} = {{U}^{{ - 1}}}{\mathbf{u}},$
где матрица ${{U}^{{ - 1}}}$ находится путем диагонализации соответствующей матрицы ${{A}_{i}}$:

(5)
$A = {{U}^{{ - 1}}}{{\Lambda }}U.$

Поскольку матрица ${{\Lambda }}$ является диагональной и состоит из собственных значений матрицы ${{A}_{i}}$, исходная система уравнений превращается в систему одномерных независимых линейных уравнений переноса:

(6)
$\frac{{\partial {\mathbf{r}}}}{{\partial t}} + {{\Lambda }}\frac{{\partial {\mathbf{r}}}}{{\partial \xi }} = 0.$

Системы уравнений, описывающие поведение акустической среды, а также модели Максвелла и Кукуджанова также являются гиперболическими (с ненулевыми правыми частями) и допускают аналогичные преобразования.

Остановимся подробнее на численном решении линейного уравнения переноса:

(7)
${{u}_{t}} + \lambda {{u}_{x}} = 0,\quad \lambda = {\text{const}}.$

Введем в рассмотрение шеститочечный шаблон: $({{t}_{{n + 1}}},{{x}_{m}})$, $({{t}_{n}},{{x}_{{m - 2}}})$, $({{t}_{n}},{{x}_{{m - 1}}}),({{t}_{n}},{{x}_{m}}),({{t}_{n}},{{x}_{{m + 1}}})$, (tn, xm + 2).

Все явные разностные схемы на данном шаблоне можно записать в виде выражения с неопределенными коэффициентами $\alpha _{{ - 2}}^{{\text{\;}}}$, $\alpha _{{ - 1}}^{{\text{\;}}}$, $\alpha _{0}^{{\text{\;}}}$, $\alpha _{1}^{{\text{\;}}},\alpha _{2}^{{\text{\;}}}$:

(8)
$u_{m}^{{n + 1}} = \alpha _{{ - 2}}^{{\text{\;}}}u_{{m - 2}}^{n} + \alpha _{{ - 1}}^{{\text{\;}}}u_{{m - 1}}^{n} + \alpha _{0}^{{\text{\;}}}u_{m}^{n} + \alpha _{1}^{{\text{\;}}}u_{{m + 1}}^{n} + \alpha _{2}^{{\text{\;}}}u_{{m + 2}}^{n}.$

А.С. Холодовым был проведен их анализ [20, 21], при котором варьировались коэффициенты $\alpha _{{ - 2}}^{{\text{\;}}}$, $\alpha _{2}^{{\text{\;}}},~\alpha _{0}^{{\text{\;}}}$. Его результаты представлены на рис. 2.

Рис. 2.

Пространство неопределенных коэффициентов из работы [22]. Заштрихованная область – схемы 1 -го порядка, монотонные по Фридрихсу [23], область ${{B}_{1}}{{B}_{2}}{{B}_{3}}{{B}_{4}}$ – все устойчивые схемы 2 -го порядка, прямая ${{C}_{1}}{\text{--}}{{C}_{5}}$ – все устойчивые схемы 3 -го порядка.

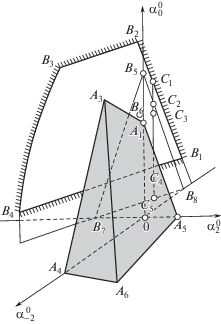
Поскольку не существует способа построить явную линейную монотонную схему выше первого порядка аппроксимации, нами был выбран подход, основанный на гибридизации вычислительного алгоритма. Для построения расчетной схемы были использованы квазимонотонные схемы [24], демонстрирующие минимальные осцилляции среди схем 2 -го и 3-го порядков, т.е. наиболее близкие по метрике $\sqrt {\mathop \sum \limits_{\mu ,\nu } {{{(\alpha _{\mu }^{\nu } - {{\alpha }_{A}}_{\mu }^{\nu })}}^{2}}} $ к области монотонных по Фридрихсу схем, схема с наименьшей аппроксимационной ошибкой среди схем 1 -го порядка, а также единственная схема 4 -го порядка и некоторые схемы 3 -го порядка на прямой ${\text{\;}}{{C}_{1}}{\text{--}}{{C}_{5}}$ (см. рис. 2). Список всех используемых схем на данном шаблоне включает в себя следующие схемы:

1. Схема 1 -го порядка Куранта–Изаксона–Риса:

(9)
$u_{m}^{{n + 1}} = u_{m}^{n} + \frac{\sigma }{2}{\text{(}}u_{{m - 1}}^{n}{\text{\;}} - u_{{m + 1}}^{n}{\text{)}}{\text{.}}$

2. Квазимонотонная схема 2 -го порядка:

(10)
$\begin{gathered} u_{m}^{{n + 1}} = u_{m}^{n} + \frac{\sigma }{2}(u_{{m - 1}}^{n}{\text{\;}}\, - \,u_{{m + 1}}^{n}){\text{\;}} + \frac{{{{\sigma }^{2}}}}{2}(u_{{m - 1}}^{n}{\text{\;}}--{\text{\;}}2u_{m}^{n}{\text{\;}} + u_{{m + 1}}^{n}) + \\ + \frac{{3\sigma (\sigma - 1)}}{{19}}(u_{{m + 2}}^{n} - 4u_{{m + 1}}^{n} + 6u_{m}^{n} - 4u_{{m - 1}}^{n} + u_{{m - 2}}^{n}). \\ \end{gathered} $

3. Схема 3 -го порядка Русанова:

(11)
$\begin{gathered} u_{m}^{{n + 1}} = u_{m}^{n} + \frac{\sigma }{2}(u_{{m - 1}}^{n} - u_{{m + 1}}^{n}) + \frac{{{{\sigma }^{2}}}}{2}(u_{{m - 1}}^{n} - 2u_{m}^{n}{\text{\;}} + u_{{m + 1}}^{n}){\text{\;}} + \\ + {\text{\;}}\frac{{{{\sigma }}(1 - {{\sigma }^{2}})}}{6}{\text{\;}}(u_{{m - 2}}^{n} - 3u_{{m - 1}}^{n} + u_{m}^{n} - u_{{m + 1}}^{n}). \\ \end{gathered} $

4. Схема 3 -го порядка (без названия):

(12)
$\begin{gathered} u_{m}^{{n + 1}} = u_{m}^{n} + \frac{\sigma }{2}(u_{{m - 1}}^{n} - u_{{m + 1}}^{n}) + \frac{{{{\sigma }^{2}}}}{2}(u_{{m - 1}}^{n} - {\text{\;}}2u_{m}^{n}{\text{\;}} + u_{{m + 1}}^{n}){\text{\;}} + \\ + \,{\text{\;}}\frac{{{{\sigma }}(1 - {{\sigma }^{2}})}}{6}(u_{{m - 2}}^{n} - 3u_{{m - 1}}^{n} + u_{m}^{n} - u_{{m + 1}}^{n}) + \\ + \frac{{(3 - 2{{\sigma }})({{\sigma }^{2}} - 1)}}{{24}}(u_{{m - 2}}^{n} - 4u_{{m - 1}}^{n} + {\text{\;}}6u_{m}^{n} - 4u_{{m + 1}}^{n} + u_{{m + 2}}^{n}). \\ \end{gathered} $

5. Квазимонотонная схема 3 -го порядка:

(13)
$\begin{gathered} u_{m}^{{n + 1}} = u_{m}^{n} + \frac{\sigma }{2}(u_{{m - 1}}^{n} - u_{{m + 1}}^{n}) + \frac{{{{\sigma }^{2}}}}{2}(u_{{m - 1}}^{n} - {\text{\;}}2u_{m}^{n}{\text{\;}} + u_{{m + 1}}^{n}){\text{\;}} + \\ + \,\frac{{{{\sigma }}(1 - {{\sigma }^{2}})}}{6}{\text{\;}}(u_{{m - 2}}^{n} - 3u_{{m - 1}}^{n} + u_{m}^{n} - u_{{m + 1}}^{n}) + \\ + \,\frac{{{{\sigma }}(17\, - \,19{{\sigma }})({{\sigma }}\, - \,1)}}{{228}}(u_{{m - 2}}^{n}\, - \,4u_{{m - 1}}^{n}\, + \,6u_{m}^{n} - 4u_{{m + 1}}^{n} + u_{{m + 2}}^{n}). \\ \end{gathered} $

6. Схема 4 -го порядка:

(14)
$\begin{gathered} u_{m}^{{n + 1}} = u_{m}^{n} + \frac{\sigma }{{12}}(u_{{m + 2}}^{n} - 8u_{{m + 1}}^{n} + 8u_{{m - 1}}^{n} - u_{{m - 2}}^{n}) - \\ - \frac{{{{\sigma }^{2}}}}{{{{{24}}^{2}}}}(u_{{m + 2}}^{n} - 16u_{{m + 1}}^{n} + 30u_{m}^{n} - 16u_{{m - 1}}^{n} + u_{{m - 2}}^{n}) - \\ - \frac{{2{{\sigma }^{3}}}}{{{{{24}}^{3}}}}(u_{{m + 2}}^{n} - 2u_{{m + 1}}^{n} + 2u_{{m - 1}}^{n} - u_{{m - 2}}^{n}) + \\ + \frac{{{{\sigma }^{4}}}}{{{{{24}}^{4}}}}(u_{{m + 2}}^{n} - 4u_{{m + 1}}^{n} + 6u_{m}^{n} - 4u_{{m - 1}}^{n} + u_{{m - 2}}^{n}). \\ \end{gathered} $

В данной работе используется сеточно-характеристический критерий монотонности:

(15)
${\text{min}}\left\{ {u_{1}^{n},u_{2}^{n}} \right\} \leqslant u_{m}^{{n + 1}} \leqslant {\text{max}}\left\{ {u_{1}^{n},u_{2}^{n}} \right\},$
где $u_{1}^{n}$, $u_{2}^{n}$ – значения сеточной функции на слое $t = {{t}_{n}}$ в двух ближайших к характеристике, исходящей из рассчитываемой точки $\left( {{{t}_{{n + 1}}},{{x}_{m}}} \right)$, сеточных узлах $x = ~\,{{x}_{1}}$, $x = ~\,{{x}_{2}}$, лежащих по обе стороны от этой характеристики.

На основе данного критерия монотонности была построена гибридная схем по следующему алгоритму:

1) Вычисление $u_{m}^{{n + 1}}$ по схеме наивысшего порядка;

2) Проверка критерия монотонности. Если он выполняется, то используется рассчитанное значение. Если он не выполняется, то вычисляется $u_{m}^{{n + 1}}$ по схеме такого же порядка или на порядок ниже.

При этом записанные выше схемы перебираются в следующем порядке: схема 4 -го порядка, схема 3 -го порядка Русанова, схема 3 -го порядка (без названия), квазимонотонная схема 3 -го порядка, квазимонотонная схема 2 -го порядка, схема 1 -го порядка Куранта–Изаксона–Риса.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

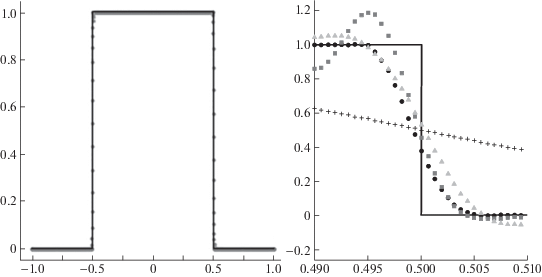
Построенная гибридная схема была протестирована на разрывном решении одномерного линейного уравнения переноса. Параметры численного расчета: число Куранта σ = 0.2, шаг по пространству h = 0.625 мм, число шагов по пространству Nx = 3200, шаг по времени $\Delta t$ = 0.125 мс, число шагов по времени Nt = 16 000. В центре расчетной области задавался прямоугольный импульс единичной амплитуды, на границах использовались периодические граничные условия.

Результаты расчетов представлены на рис. 3. Их анализ показывает, что гибридная схема обеспечивает отсутствие нефизических осцилляций, в отличие от остальных схем с порядком аппроксимации выше 1-го. При этом она значительно превосходит схему 1 -го порядка по узости размытия разрыва и близка к схемам 3 -го и 4-го порядка аппроксимации.

Рис. 3.

Слева – численный расчет по гибридной схеме () и аналитическое решение (—). Справа – окрестность правой границы импульса: схема 4 -го порядка (), 3-го порядка Русанова (), гибридная схема (), 1-го порядка Куранта–Изаксона–Риса (), аналитическое решение (—).

В дальнейшем построенная схема была использована при расчете задачи об источнике сейсмического сигнала в ледовом острове. Всего в расчете использовалось порядка 180 тыс. узлов сетки, а шаг по времени, выбранный из условия Куранта, составлял 5 мкс. На рис. 4 представлены результаты проведенных расчетов для модели с резервуаром с метаном и без него. Видно образование отраженных от его покрышки и подошвы упругих волн, регистрация которых на дневной поверхности должна позволить определить характеристики резервуара. Вдоль поверхности по льду распространяется поверхностная волна Рэлея, а в остальных слоях продольные и поперечные объемные волны.

Рис. 4.

Распределение модуля скорости в модели в момент времени 0.3 с после начала расчета. Слева – отсутствие резервуара, справа – его наличие. Обозначения: a – продольные волны, отраженные от покрышки и подошвы резервуара, b и c – сферические волны от его боковых границ, d – зона ослабления падающей волны.

ЗАКЛЮЧЕНИЕ

В настоящей работе была рассмотрена задача распространения волн при проведении сейсмической разведки с ледового острова. В модель исследуемой области входили лед, водная толща и геологический массив с резервуаром, заполненным метаном. Для описания динамического поведения данных сред использовался ряд механико-математических моделей, определяющие системы уравнений которых являются гиперболическими. Для их численного решения использовался сеточно-характеристический метод на прямоугольных сетках с явным выделением контактных границ. Он включает этап решения линейного одномерного уравнения переноса, для которого была построена новая гибридная схема повышенного порядка точности. Она продемонстрировала отсутствие нефизических осцилляций на разрывных решениях.

С ее помощью были получены волновые картины процессов, происходящих во льду, воде и толще геологического массива. При наличии в модели резервуара с метаном (см. рис. 4), происходит формирование отраженных продольных волн от его покрышки и подошвы. Они несут информацию о его мощности (разница их времен прихода), а также горизонтальной протяженности (размер горизонтальных участков синфазности сигналов). Анализ пространственной волновой картины выявляет также образование сферических волн, инициированных на краях резервуара. Дополнительно следует отметить формирование зоны тени непосредственно под резервуаром, что обусловлено отражением значительной части энергии от контрастной границы геологический массив – резервуар с метаном, и дифрагированных волн. Регистрация отраженных сигналов на дневной поверхности должна способствовать определению физических характеристик резервуара.

Развитие методов решения прямых полноволновых задач способно повысить точность решения ряда практических задач. К ним относятся, в частности, выбор оптимальной схемы расстановки источников и приемников на основе априорных знаний о геологическом строении массива, оценка применимости ледовых островов для полевых работ в Арктическом регионе и влияния различных природных факторов на получаемые результаты. Разработанный вычислительный алгоритм расчета волнового поля в заданной геологической модели может быть включен в процесс решения востребованных на практике обратных задач миграции и инверсии. Направлением дальнейших исследований представляется обобщение расчетного алгоритма на трехмерный случай и использование более реалистичной геологической модели.

Список литературы

  1. Crawford A.J., Mueller D.R., Humphreys E.R., Carrieres T., Tran H. Surface ablation model evaluation on a drifting ice island in the Canadian Arctic // Cold Regions Science and Technology. 2015. V. 110. P. 170–182.

  2. Crawford A., Crocker G., Mueller D., Desjardins L., Saper R., Carrieres T. The Canadian ice island drift, deterioration and detection (CI2D3) database // Journal of Glaciology. 2018. V. 64 (245). P. 517–521.

  3. Muratov M.V., Biryukov V.A., Konov D.S., Petrov I.B. Mathematical modeling of temperature changes impact on artificial ice islands // Radioelektronika, Nanosistemy, Informacionnye Tehnologii. 2021. V. 13 (1). P. 79–86.

  4. Ladanyi B. Rheology of ice/rock systems and interfaces // Permafrost, Phillips, Springman & Arenson (eds), 2003.

  5. Golubev V.I., Shevchenko A.V., Petrov I.B. Application of the Dorovsky model for taking into account the fluid saturation of geological media // Journal of Physics: Conference Series. 2021. V. 1715 (1). № 012056.

  6. Golubev V.I., Vasyukov A.V., Churyakov M. Modeling Wave Responses from Thawed Permafrost Zones // Smart Innovation, Systems and Technologies. 2021. V. 214. P. 137–148.

  7. Petrov I.B., Muratov M.V., Sergeev F.I. Elastic Wave Propagation Modeling During Exploratory Drilling on Artificial Ice Island // Smart Innovation, Systems and Technologies. 2021. V. 217. P. 171–183.

  8. Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1970.

  9. Александров К.С., Продайвода Г.Т. Анизотропия упругих свойств минералов и горных пород, 2000.

  10. Petrov I.B., Kholodov A.S. Numerical investigation of certain dynamical problems of the mechanics of a deformable solid body by the grid-characteristic method // U.S.S.R. Comput. Math. Math. Phys. 1984. V. 24 (3). P. 61–73.

  11. Работнов Ю. Н. Механика деформируемого твердого тела. М.: Наука, 1988.

  12. Stankiewicz A. Fractional Maxwell model of viscoelastic biological materials // BIO Web Conf. 2018. V. 10. 02032.

  13. Годунов С.К., Роменский Е.И. Элементы механики сплошных сред и законы сохранения. Город. 1998.

  14. Кукуджанов В.Н. Численное решение неодномерных задач распространения волн напряжений в твердых телах. М., 1976. 66 с.

  15. Golubev V.I., Shevchenko A.V., Khokhlov N.I., Nikitin I.S. Numerical investigation of compact grid-characteristic schemes for acoustic problems // Journal of Physics: Conference Series, 2021, 1902 (1), № 012110.

  16. Beklemysheva K.A., Golubev V.I., Petrov I.B., Vasyukov A.V. Determining effects of impact loading on residual strength of fiber-metal laminates with grid-characteristic numerical method // Chinese Journal of Aeronautics. 2021. V. 34 (7). P. 1–12.

  17. Konyagin S., Popov B., Trifonov O. On Convergence of Minmod-Type Schemes // SIAM J. Numerical Analysis. 2005. 42. P. 1978–1997.

  18. Shu C.-W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws // Advanced Numerical Approximation of Nonlinear Hyperbolic Equations. 2006. P. 325–432.

  19. Harten A. High resolution schemes for hyperbolic conservation laws // Comput. Phys. 1987. V. 49 (3). P. 357–393.

  20. Petrov I.B., Kholodov A.S. Regularization of discontinuous numerical solutions of equations of hyperbolic type // U.S.S.R. Comput. Math. Math. Phys. 1984. V. 24 (4). P. 128–138.

  21. Kholodov A.S., Kholodov Y.A. Monotonicity criteria for difference schemes designed for hyperbolic equations // Comput. Math. and Math. Phys. 2006. V. 46. P. 1560–1588.

  22. Kholodov A. S. The construction of difference schemes of increased order of accuracy for equations of hyperbolic type // USSR Computational Mathematics and Mathematical Physics. 1980. V. 20 (6). P. 234–253.

  23. Fridrichs K.O. Symmetric hyperbolic linear differential equations // IBID. 1954. V. 2. P. 345–392.

  24. Магомедов К.М., Холодов А.С. Сеточно-характеристические численные методы. М.: Наука, 2018. 287 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал