1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 501, № 1, 2021

Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 501, № 1, стр. 26-30

О максимальном разрезе в случайном гиперграфе

П. А. Захаров 1, *, Д. А. Шабанов 1, 2, 3, **

1 Национальный исследовательский университет “Высшая школа экономики”
Москва, Россия

2 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

3 Московский государственный университет имени М.В. Ломоносова
Москва, Россия

* E-mail: pazakharov@hse.ru
** E-mail: dmitry.shabanov@phystech.edu

Поступила в редакцию 11.08.2021
После доработки 17.08.2021
Принята к публикации 08.09.2021

Полный текст (PDF)

Аннотация

Исследуется задача о нахождении максимального разреза в случайных гиперграфах. Рассматривается классическая биномиальная модель случайного $k$-однородного гиперграфа $H(n,k,p)$ на $n$ вершинах и вероятностью $p = p(n)$. Основные результаты обобщают ранее известные результаты для случая графов и показывают, что в разреженном случае (когда $p = cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)$ при $c = c(k) > 0$, не зависящем от $n$) существует такая $\gamma (c,k,q) > 0$, что отношение величины максимального разреза $H(n,k,p)$ к числу вершин сходится к ней по вероятности. Кроме того, получены некоторые оценки величины $\gamma (c,k,q)$.

Ключевые слова: гиперграфы, случайные гиперграфы, разрез гиперграфа, метод интерполяции, задачи оптимизации

1. ВВЕДЕНИЕ

Настоящая работа посвящена исследованию задачи о поиске максимального разреза в случайных гиперграфах. Начнем с основных определений.

Гиперграфом $H$ в дискретной математике называется пара $(V,E)$, где $V = V(H)$ – это некоторое конечное множество, элементы которого мы будем называть вершинами гиперграфа, а $E = E(H)$ – это семейство подмножеств $V$, которые мы будем называть ребрами гиперграфа. Гиперграф $H = (V,E)$ называется $k$-однородным, если для любого $e \in E(H)$ выполнено $\left| e \right| = k$, т.е. все ребра гиперграфа имеют одну и ту же мощность k. С точки зрения теории графов получается, что граф – это 2-однородный гиперграф без петель и кратных ребер.

Если $q \geqslant 2$ – это натуральное число, то q-разрезом гиперграфа H называется разбиение множества вершин $V(H)$ на q непересекающихся подмножеств: ${{V}_{1}} \sqcup {{V}_{2}} \sqcup \ldots \sqcup {{V}_{q}} = V(H)$. Величиной разреза $({{V}_{1}}, \ldots ,{{V}_{q}})$ называется величина 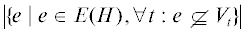, другими словами – это количество ребер, которые не содержатся ни в одном из элементов разреза целиком. Максимальным q-разрезом в $H$ называется максимальная величина q-разреза по всем разбиениям множества вершин, для нее будем использовать обозначение ${{\mu }_{q}}(H)$.

Несложно понять, что задачу о поиске максимального разреза можно сформулировать и в терминах раскрасок. Ясно, что q-разрез – это просто раскраска вершин гиперграфа в q цветов, а его величина – это количество ребер, которые покрашены неодноцветно в такой раскраске. Тем самым, максимальный разрез равен максимально возможному количеству ребер, которые можно правильно (т.е. неодноцветно) раскрасить в одной и той же раскраске вершин гиперграфа в q цветов.

В работе мы исследуем максимальный разрез случайных гиперграфов в биномиальной модели. Напомним, что классической биномиальной моделью случайного k-однородного гиперграфа, $H(n,k,p)$, называется схема Бернулли на k-подмножествах некоторого $n$-элементного множества $V$ вершины: каждое из них включается в качестве ребра в $H(n,k,p)$ с вероятностью $p = p(n)$ независимо от прочих. Несложно заметить, что вероятность получить конкретный k-однородный гиперграф $H{\kern 1pt} ' = (V,E{\kern 1pt} ')$ равна

$\Pr \left( {H(n,k,p) = H{\kern 1pt} '(V,E{\kern 1pt} ')} \right) = {{p}^{{|E{\kern 1pt} '|}}} \cdot {{(1 - p)}^{{\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right) - |E{\kern 1pt} '|}}}.$

При k = 2 данная модель — это знаменитая модель  Эрдеша–Реньи, обозначаемая $G(n,p)$. В настоящей работе мы исследуем величину ${{\mu }_{q}}(H(n$, k, p)) при фиксированных q и k, растущем $n \to + \infty $ и $p = p(n)$.

2. ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ

Задача об асимптотической оценке максимального q-разреза в случайном графе $G(n,p)$ наиболее интересна в разреженном случае, т.е. когда $p = cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right)$ и $c > 0$, не зависящем от n. Если $np \to + \infty $, то легко заметить, что

${{\mu }_{q}}(G(n,p))\,\,\mathop \sim \limits^{\Pr } \,\,\left( {1 - \frac{1}{q}} \right)p\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right).$

Если же $np \to 0$, то с большой вероятностью можно разрезать все ребра случайного графа,

$\Pr ({{\mu }_{q}}(G(n,p)) = {\text{|}}E(G(n,p))){\text{|}}) \to 1\quad {\text{при}}\quad n \to + \infty .$

Тем самым, ситуация наиболее нетривиальна при фиксированном значении np. Здесь фундаментальным результатом является теорема М. Байати, Д. Гамарника и П. Тетали [1]. В ней было установлено существование предела для следующей сходимости по вероятности:

$\frac{{{{\mu }_{q}}\left( {G\left( {n,cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right)} \right)} \right)}}{n}\mathop \to \limits^{\Pr } \gamma (c,q)\quad {\text{при}}\quad n \to + \infty .$

Но авторами было лишь установлено существование предела, а не его точное значение. Значительные исследования были посвящены поиску асимптотических оценок величины $\gamma (c,q)$ при c достаточно большом по отношению к q (о предельном распределении максимального разреза при малом c см. [2]). Исследователями было показано, что имеет место представление следующего вида:

$\gamma (c,q) = (1 - {{q}^{{ - 1}}}) \cdot c + {{B}_{q}} \cdot \sqrt c + o(\sqrt c ),$
в котором предпринимались попытки найти значение параметра ${{B}_{q}}$. В 1997 г. для случая $q = 2$ А. Бертони и др. [3] доказали, что ${{B}_{2}} \leqslant \sqrt {\frac{{\ln 2}}{2}} $. В дальнейшем Д. Копперсмит с соавторами [4] показал, что ${{B}_{2}} \in [0.37613,0.58870]$. Д. Гамарник и К. Ли [5] улучшили эти оценки, показав, что ${{B}_{2}} \in [0.47523,0.55909]$. Наконец, А. Дембо, А. Монтанари и С. Сен [6] вычислили точное значение величины ${{B}_{2}}$, которое может быть представлено в виде решения некоторого дифференциального уравнения.

Случай $q > 2$ на сегодняшний день изучен не столь детально. А. Койя-Оглан, К. Мур и В. Санвалани [7] получили следующие оценки параметра ${{B}_{q}}$ для достаточно больших значений q:

$\frac{4}{3}\sqrt {\frac{{\ln q}}{q}} \left( {1 - O\left( {\frac{{\ln \ln q}}{{\ln q}}} \right)} \right) \leqslant {{B}_{q}} \leqslant \sqrt {\frac{{2\ln q}}{q}} \sqrt {1 - \frac{1}{q}} .$

Целью нашей работы является обобщение вышеупомянутых результатов для случайных гиперграфов.

Авторы также хотели бы обратить внимание читателя на ряд свежих близких работ по раскраскам случайных гиперграфов в разреженном случае [8–14].

3. НОВЫЕ РЕЗУЛЬТАТЫ

Наш первый результат устанавливает существование предела для нормированного максимального q-разреза случайного k-однородного гиперграфа в разреженном случае, т.е. при $p = cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)$ и некотором $c > 0$, не зависящем от $n$.

Теорема 1. Для любых фиксированных $k \geqslant 3$, $q \geqslant 2$, c > 0 и $p = cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)$ существует такая величина $\gamma (c,k,q)$, что

$\frac{{{{\mu }_{q}}(H(n,k,p))}}{n}\mathop \to \limits^{\Pr } \gamma (c,k,q),\quad при\quad n \to + \infty .$

Данная теорема является обобщением результата из [1] и лишь устанавливает существование предела, но не дает представления о значении величины $\gamma (c,k,q)$. Следующая теорема дает некоторые оценки $\gamma (c,k,q)$ в предположении, что $c$ достаточно велико по сравнению с k и q.

Теорема 2. Для любого достаточно большого $c > {{c}_{0}}(k,q)$ выполнены неравенства

$\gamma (c,k,q) \leqslant c \cdot (1 - {{q}^{{1 - k}}}) + \sqrt c \cdot {{A}_{{k,q}}} + o(\sqrt c ),$
$\gamma (c,k,q) \geqslant c \cdot (1 - {{q}^{{1 - k}}}) + \sqrt c \cdot {{C}_{{k,q}}} + o(\sqrt c ),$
где

${{A}_{{k,q}}} = \frac{1}{{{{q}^{{k - 1}}}}} \cdot \sqrt {2\ln q \cdot ({{q}^{{k - 1}}} - 1)} ,$
${{C}_{{k,q}}} = \frac{{\sqrt {8\ln q} }}{{k + 1}} \cdot \sqrt {\frac{k}{{{{q}^{{k - 1}}}}}} \cdot \left( {1 - O\left( {\frac{{\ln \ln q}}{{\ln q}}} \right)} \right).$

Данная теорема обобщает результаты из [3] и [7]. Можно заметить, что для достаточно большого q мы получаем зазор порядка $\sqrt k $ между имеющимися границами.

Далее мы приведем основные идеи доказательств.

4. ИДЕИ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ 1

Доказательство теоремы 1 основано на применении техники из работы [1] и использует метод интерполяции. Заметим, что нам достаточно доказать существование предела для нормированного математического ожидания величины максимального разреза:

$\gamma (c,k,q) = \mathop {\lim }\limits_{n \to + \infty } \frac{{{\text{E}}{{\mu }_{q}}\left( {H\left( {n,k,cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)} \right)} \right.}}{n}.$

Данный факт следует из того, что величина максимального q-разреза случайного гиперграфа ${{\mu }_{q}}\left( {H\left( {n,k,cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)} \right)} \right.$ сильно сконцентрирована вокруг своего среднего значения, что может быть установлено с помощью неравенства Талаграна (см. [15, с. 41–42]).

Дальнейшая идея состоит в проверке того, что последовательность

$a(n) = {\text{E}}{{\mu }_{q}}\left( {H\left( {n,k,cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)} \right)} \right)$
является почти супераддитивной, т.е. что
$a(n) \geqslant a({{n}_{1}}) + a({{n}_{2}}) - O({{n}^{{1/2}}})$
для любых $n,{{n}_{1}},{{n}_{2}}$, таких что ${{n}_{1}} + {{n}_{2}} = n$. Базовые факты из анализа показывают, что в таком случае существует предел последовательности $a(n){\text{/}}n$.

Далее, зафиксируем $n,{{n}_{1}},{{n}_{2}}$ с условием, что ${{n}_{1}} + {{n}_{2}}$ = n, и применим метод интерполяции. Обозначим через $V$ множество из n вершин, ${\text{|}}V{\text{|}} = n$. Зафиксируем произвольным образом его разбиение на две непересекающиеся части ${{V}_{1}}$ и ${{V}_{2}}$, ${\text{|}}{{V}_{i}}{\text{|}} = {{n}_{i}}$, i = 1, 2. Образуем следующую последовательность случайных гиперграфов с множеством вершин $V$: ${{H}^{{(t)}}}(n,k,m)$, $t = 0, \ldots ,m$, где $m = \left\lfloor {cn} \right\rfloor $. Гиперграф ${{H}^{{(t)}}}(n,k,m)$ состоит из так называемых t зеленых ребер и $m - t$ красных ребер, все ребра случайны и выбираются независимо.

Зеленое ребро выбирается равновероятно из ${{V}^{k}}$ (другими словами, мы выбираем $k$ вершин с повторениями).

Красное ребро выбирается из $V_{i}^{k}$, $i = 1,2$, с вероятностью ${{n}_{i}}{\text{/}}n$ (другими словами, мы сначала выбираем пропорционально одну из частей, а затем в ней выбираем k вершин с повторениями).

Заметим, что ${{H}^{{(t)}}}(n,k,m)$ может содержать как кратные, так и неполные (менее k различных вершин) ребра. Тем не менее, ${{H}^{{(m)}}}(n,k,m)$ выглядит как классическая равномерная модель с m ребрами, а ${{H}^{{(0)}}}(n,k,m)$ выглядит как объединение двух непересекающихся меньших гиперграфов ${{H}^{{({{m}_{i}})}}}(n,k,{{m}_{i}})$, 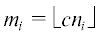, $i = 1,2$. Следующая лемма является ключевой для установления искомого предела и показывает суть метода интерполяции.

Лемма 1. Для любого $t = 1, \ldots ,m$

После доказательства леммы остается, применяя технику каплинга, аппроксимировать модели и показать, что

$\begin{gathered} \left| {{\text{E}}{{\mu }_{q}}({{H}^{{(m)}}}(n,k,m)) - {\text{E}}{{\mu }_{q}}\left( {H\left( {n,k,cn{\text{/}}\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)} \right)} \right)} \right| = \\ = O({{n}^{{1/2}}}). \\ \end{gathered} $

5. НИЖНЯЯ ОЦЕНКА В ТЕОРЕМЕ 2

При доказательстве нижней оценки мы воспользуемся идеями из работ [4–7] и будем применять жадный алгоритм набора разреза. Будем красить вершины по очереди следующим образом: присвоим вершине такой цвет i, который добавит в разрез максимальное количество ребер. На шаге t обозначим через $z(t)$ число ребер, добавленных в разрез, а через $m(t)$ – число новых образованных одноцветных ребер. Следующая лемма позволяет оценить среднее значение величины $z(t)$.

Лемма 2.

${\text{E}}z(t) \geqslant \frac{{cn}}{{\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)}} \cdot \left( {\begin{array}{*{20}{c}} t \\ {k - 1} \end{array}} \right) - $
$\begin{gathered} - \left( {\frac{{c \cdot {{{(t{\text{/}}n)}}^{{k - 1}}} \cdot k}}{{{{q}^{{k - 1}}}}} + {{r}_{q}} \cdot \sqrt {\frac{{c \cdot {{{(t{\text{/}}n)}}^{{k - 1}}} \cdot k}}{{{{q}^{{k - 1}}}}}} } \right) \times \\ \times \left( {1 + O\left( {\frac{1}{n}} \right)} \right) + o(\sqrt c ), \\ \end{gathered} $
где ${{r}_{q}} = \min \{ {{\xi }_{1}}, \ldots ,{{\xi }_{q}}\} $, ${{\xi }_{i}}$ суть независимые стандартные нормальные случайные величины.

В ходе доказательства мы сначала оцениваем среднее величины $m(t)$. Так как наихудший случай есть равномерная раскраска в q цветов, то

${\text{E}}m(t) \leqslant {\text{E}}\min \{ {{u}_{1}}, \ldots ,{{u}_{q}}\} ,$
где ${{u}_{q}}, \ldots ,{{u}_{q}}$ – это независимые случайные величины с распределением ${\text{Bin}}\left( {\left( {\begin{array}{*{20}{c}} {t{\text{/}}q} \\ {k - 1} \end{array}} \right),p} \right)$. Далее мы используем ряд предельных теорем, получая аппроксимацию нормальным распределением. На заключительном шаге мы оцениваем сумму $\sum\limits_{t = 1}^{n - 1} {{\text{E}}m(t)} $, используя выражение из леммы 2. В результате аккуратного анализа получаем искомое.

6. ВЕРХНЯЯ ОЦЕНКА В ТЕОРЕМЕ 2

Здесь мы следуем идеям из [3]. Для упрощения анализа переходим к равномерной модели $H(n,m$, k), где мы равновероятно выбираем 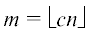k‑элементных подмножеств без повторений. Чтобы показать, что некоторая величина x является верхней оценкой максимального q-разреза, мы оцениваем число k-однородных гиперграфов на $n$ вершинах с $m$ ребрами и максимальным разрезом, большим чем x.

Для гиперграфа $H = (V,E)$ рассмотрим некоторое разбиение вершин $V = {{V}_{1}} \sqcup \ldots \sqcup {{V}_{q}}$. Обозначим через ${{E}_{i}}$ множество ребер, целиком содержащихся в ${{V}_{i}}$, а через ${{E}_{0}}$ – все оставшиеся ребра.

Обозначим $T = ({{V}_{1}}, \ldots ,{{V}_{q}},{{E}_{0}}, \ldots ,{{E}_{q}})$ и рассмотрим множество всех подобных наборов для всевозможных k-однородных гиперграфов с множеством вершин V, $m$ ребрами и ${\text{|}}{{E}_{0}}{\text{|}} \geqslant x$:

$t(n,m,k,q,x) = {\text{|}}\{ T:{\text{|}}{{E}_{0}}{\text{|}} \geqslant x\} {\text{|}} = $
$ = \sum\limits_{\substack{ {{n}_{1}}, \ldots ,{{n}_{q}} \\ {{m}_{1}}, \ldots ,{{m}_{q}} } } \left| {\left\{ {T{\text{:}}\,\,{\text{|}}{{V}_{i}}{\text{|}} = {{n}_{i}},{\text{|}}{{E}_{i}}{\text{|}} = {{m}_{i}},{\text{|}}{{E}_{0}}{\text{|}} \geqslant x} \right\}} \right|.$

Обозначим через $h(n,m,k,q,x)$ максимальное слагаемое в вышеописанной сумме. Следующая лемма характеризует предельное поведение этой величины.

Лемма 3.

$h(n,m,k,q,x) \sim \frac{{n!}}{{{{{((n{\text{/}}q)!)}}^{q}}}} \cdot {{\left( {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {n{\text{/}}q} \\ k \end{array}} \right)} \\ {\frac{{m - x}}{q}} \end{array}} \right)}^{q}} \cdot \left( {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right) - q \cdot \left( {\begin{array}{*{20}{c}} {n{\text{/}}q} \\ k \end{array}} \right)} \\ x \end{array}} \right).$

Доказательство основано на решении соответствующей оптимизационной задачи. Лемма 3 помогает оценить вероятность того, что максимальный разрез случайного гиперграфа $H(n,m,k)$ превосходит $x$. А именно, эта вероятность меньше, чем

$\frac{{h(n,m,k,q,x) \cdot {{n}^{{q - 1}}} \cdot {{{({{n}^{k}})}}^{q}}}}{{\left( {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)} \\ m \end{array}} \right)}}.$

Остается показать, что эта величина стремится к нулю при

$x = n \cdot (c \cdot (1 - {{q}^{{1 - k}}}) + \sqrt c \cdot {{A}_{{k,q}}} + o(\sqrt c )).$

Список литературы

  1. Bayati M., Gamarnik D., Tetali P. Combinatorial approach to the interpolation method and scaling limits in sparse random graphs // The Annals of Probability. 2013. V. 41. P. 4080–4115. https://doi.org/10.1214/12-AOP816

  2. Daudé H., Martinez C., Rasendrahasina V., Ravelomanana V. The max-cut of sparse random graphs // Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms. SIAM. 2012. P. 265–271. https://doi.org/10.1137/1.9781611973099.24

  3. Bertoni A., Campadelli P., Posenato R. An Upper Bound for the Maximum Cut Mean Value // Lecture Notes in Computer Science. 1997. V. 1335. P. 78–84. https://doi.org/10.1007/BFb0024489

  4. Coppersmith D., Gamarnik D., Hajiaghayi M., Sorkin G. Random maxsat, random maxcut, and their phase transitions // Random Structures and Algorithms. 2004. V. 24. P. 502–545. https://doi.org/10.1002/rsa.20015

  5. Gamarnik D., Li Q. On the max-cut over sparse random graph // Random Structures and Algorithms. 2018. V. 52. P. 219–262. https://doi.org/10.1002/rsa.20738

  6. Dembo A., Montanari A., Sen S. Extremal cuts of sparse random graphs // The Annals of Probability. 2017. V. 45. P. 1190–1217. https://doi.org/10.1214/15-AOP1084

  7. Coja-Oghlan A., Moore C., Sanwalani V. Max k-cut and approximating the chromatic number of random graphs // Random Structures and Algorithms. 2006. V. 28. P. 289–322. https://doi.org/10.1002/rsa.20096

  8. Kravtsov D.A., Krokhmal N.E., Shabanov D.A. Panchromatic 3-colorings of random hypergraphs // European Journal of Combinatorics. 2019. V. 78. P. 28–43. https://doi.org/10.1016/j.ejc.2019.01.006

  9. Ayre P., Coja-Oghlan A., Greenhill C. Hypergraph coloring up to condensation // Random Structures and Algorithms. 2019. V. 54. № 4. P. 615–652. https://doi.org/10.1002/rsa.20824

  10. Ayre P., Greenhill C. Rigid colorings of hypergraphs and contiguity. SIAM Journal on Discrete Mathematics. 2019. V. 33. P. 1575–1606.

  11. Семенов А.С. Двухцветные раскраски случайного гиперграфа // Теория вероятностей и ее применения. 2019. Т. 64. № 1. С. 75–97. https://doi.org/10.4213/tvp5165

  12. Semenov A., Shabanov D. On the weak chromatic number of random hypergraphs // Discrete Applied Mathematics. 2020. V. 276. P. 134–154. https://doi.org/10.1016/j.dam.2019.03.025

  13. Shabanov D.A. Estimating the r-colorability threshold for a random hypergraph // Discrete Applied Mathematics. 2020. V. 282. P. 168–183. https://doi.org/10.1016/j.dam.2019.10.031

  14. Balobanov A. E., Shabanov D. A. On the strong chromatic number of a random 3-uniform hypergraph // Discrete Mathematics. 2021. V. 344. № 3. P. 1–16. https://doi.org/10.1016/j.disc.2020.112231

  15. Janson S., Łuczak T., Ruciński A. Random Graphs. New York: Wiley, 2000. 335 pp.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал