Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 502, № 1, стр. 23-27

1. ВВЕДЕНИЕ

Рассматриваются связанные в цепочку осцилляторы на базе логистического уравнения с запаздыванием

Уравнение (1) играет важную роль во многих прикладных задачах биофизики, математической экологии, лазерной физики и др. [1–4]. Функция $u(t)$ неотрицательна и r > 0. Свойства уравнения (1) хорошо известны (см., например, [4–6]). Отметим, что при $0 < r < \frac{\pi }{2}$ состояние равновесия ${{u}_{0}} = 1$ асимптотически устойчиво, а при $r > \frac{\pi }{2}$ – неустойчиво и в (1) имеется устойчивый цикл.

Сначала введем в рассмотрение кольцевую систему $N$ связанных уравнений

где $j = 1, \ldots ,N$, ${{u}_{0}} \equiv {{u}_{N}}$, ${{u}_{{N + 1}}} \equiv {{u}_{1}}$. При условии d > 0 связь, определяемая последним слагаемым в правой части (2), называют диффузионной, а при d < 0 – антидиффузионной. С точки зрения приложений к математической экологии условие d < 0 в уравнении (2) смысла не имеет, поскольку не выполняется условие инвариантности области ${{u}_{j}} \geqslant 0$ $(j = 1, \ldots ,N)$. Антидиффузионная связь в несколько иной постановке характерна, например, в моделях взаимодействующих конкурирующих популяций,

Значение ${{u}_{j}}(t)$ удобно связать со значением функции двух переменных $u(t,x)$ в точке некоторой окружности с угловой координатой ${{x}_{j}} = 2\pi {{N}^{{ - 1}}}j$ $(j = 1, \ldots ,N)$. Будем предполагать, что количество N точек окружности достаточно велико, т.е.

В этой ситуации от системы (3) естественно перейти к уравнению с непрерывной пространственной переменной относительно $u(t,x)$:

с периодическими краевыми условиями

Рассмотрим уравнение со связью более общего вида. Такая связь означает, что влияние одного элемента цепочки тем меньше, чем больше расстояние между элементами. Рассмотрим краевую задачу

где $F(s,\varepsilon ) = {{F}_{ + }}(s,\varepsilon ) + {{F}_{ - }}(s,\varepsilon )$,

Отметим, что при $\sigma \to 0$ в (7) приходим к уравнению (5).

Поставим задачу исследования при малом $\varepsilon $ всех решений краевой задачи (7), (6) с начальными условиями из некоторой достаточно малой и не зависящей от $\varepsilon $ окрестности состояния равновесия ${{u}_{0}} \equiv 1$. Тем самым речь идет об изучении динамики распределенных цепочек логистических уравнений с запаздыванием. Отметим, что исследованию динамики в различных цепочках связанных систем были посвящены результаты многих авторов (см., например, [7–12]). В настоящей работе используются специальные методы локального анализа [13–15]. На их основе строятся так называемые квазинормальные формы, которые представляют собой нелинейные краевые задачи, не содержащие малых параметров. Изучение нелокальной динамики этих краевых задач позволит ответить на вопрос о структуре решений исходной системы уравнений в окрестности состояния равновесия ${{u}_{0}}$.

Приведем сначала результаты, которые вытекают непосредственно из линейного анализа краевой задачи (7), (6). Рассмотрим линеаризованную на ${{u}_{0}}$ краевую задачу

Характеристическое уравнение для (9), (10) имеет вид

В том случае, когда все корни (11) (при всех $k = 0, \pm 1, \ldots $) имеют отрицательные вещественные части и отделены от нуля при $\varepsilon \to 0$, нулевое решение (9), (10) и состояние равновесия ${{u}_{0}}$ в (7), (6) асимптотически устойчиво, причем все решения из некоторой независящей от $\varepsilon $ окрестности ${{u}_{0}}$ стремятся к ${{u}_{0}}$ при $t \to \infty $. Тем самым локальная динамика в таком случае тривиальна.

Если же (11) имеет корень с положительной и отделенной от нуля при $\varepsilon \to 0$ вещественной частью, то задача о динамике в окрестности ${{u}_{0}}$ краевой задачи (7), (6) становится нелокальной: решение ${{u}_{0}}$ неустойчиво и в некоторой достаточно малой не зависящей от $\varepsilon $ его окрестности не может быть аттракторов этой краевой задачи.

Будем рассматривать критический случай, когда среди корней (11) нет корней с положительной и отделенной от нуля при $\varepsilon \to 0$ вещественной частью, но есть корень, вещественная часть которого стремится к нулю при $\varepsilon \to 0$. Необходимым условием реализации критического случая является выполнение неравенств

Будет показано, что в критическом случае бесконечно много корней (11) стремятся к мнимой оси при $\varepsilon \to 0$, т.е. реализуется критический в задаче об устойчивости случай бесконечной размерности. Используя методику работ автора [13–15], будут построены специальные нелинейные краевые задачи, которые играют роль нормальных форм для (7), (6). Их нелокальная динамика будет определять при малых $\varepsilon $ локальное, в окрестности ${{u}_{0}}$, поведение всех решений исходной краевой задачи (7), (6). Этот результат можно интерпретировать как принцип сведения (7), (6) к наиболее простым уравнениям, которые позволяют описать структуру и найти асимптотику решений (7), (6) по решениям построенных квазинормальных форм.

2. ЛИНЕЙНЫЙ АНАЛИЗ В КРИТИЧЕСКОМ СЛУЧАЕ

Сначала определим пороговое значение $d(r)$ параметра d, при котором реализуется критический случай. Для этого обозначим $z = \varepsilon k$ и предположим, что в (11) существует чисто мнимый корень $\lambda = i\omega $, $\omega = {{\omega }_{z}} \geqslant 0$. В результате приходим к уравнению

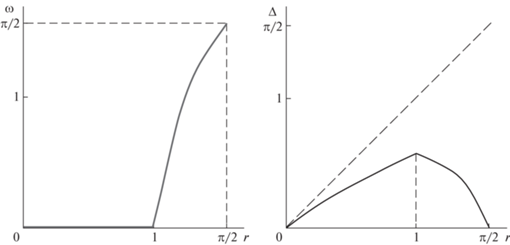
Введем несколько обозначений. Пусть $\mathop {\max }\limits_z \rho (z)$ = = ρ(z₀), т.е. ${{z}_{0}}$ – корень из интервала $\left( {\frac{\pi }{2},\pi } \right)$ уравнения tg$(z) = ( - 2{{\sigma }^{2}})z$ и $\rho {\kern 1pt} '{\kern 1pt} '({{z}_{0}}) < 0$. Через $\Delta (r)$ обозначим наименьшее неотрицательное значение параметра $\Delta $, при котором уравнение (13) имеет решение $\omega = {{\omega }_{\Delta }} \geqslant 0$. Отметим, что ${{\omega }_{\Delta }} < r$ при $0 < r < \frac{\pi }{2}$ и ${{\omega }_{\Delta }} = 0$ при $0 < r \leqslant 1$, ${{\omega }_{{\frac{\pi }{2}}}} = \frac{\pi }{2}$. При $1 < r < \frac{\pi }{2}$ выражение ${{\omega }_{\Delta }}$ является корнем на интервале $\left( {0,\frac{\pi }{2}} \right)$ уравнения ${\text{tg}}\omega = \omega {{({{r}^{2}} - {{\omega }^{2}})}^{{ - \frac{1}{2}}}}$. Положим $d(r) = {{\Delta }_{ \pm }}(r){{\rho }^{{ - 1}}}({{z}_{0}})$.

Лемма 1. Имеет место равенство

Отсюда вытекает, что при $0 < d < d(r)$ нулевое решение в (9), (10) устойчиво, а при $d > d(r)$ – неустойчиво. Критический случай реализуется при $d = d(r)$. Графики $\Delta (r)$ и $\omega (r)$ приведены на рис. 1.

Пусть ${{r}_{0}} \in \left( {0,\frac{\pi }{2}} \right]$. Фиксируем произвольно значения ${{r}_{1}}$ и ${{d}_{1}}$ и рассмотрим близкий к критическому в задаче об устойчивости решений (9), (10) случай, когда

Выпишем асимптотику всех тех корней ${{\lambda }_{m}}(\varepsilon ),{{\bar {\lambda }}_{m}}(\varepsilon )\,\,(m = 0, \pm 1, \ldots )$ уравнения (11), вещественные части которых стремятся к нулю при $\varepsilon \to 0$. Для этого понадобятся еще обозначения. Пусть $\theta = \theta (\varepsilon ) \in [0,1)$ такое значение, которое дополняет до целого выражение ${{z}_{0}}{{\varepsilon }^{{ - 1}}}$. Через ${{{v}}_{m}}(t,x,\varepsilon )$ обозначим решение (9), (10), отвечающее корню ${{\lambda }_{m}}(\varepsilon )$ уравнения (11):

Лемма 2. Пусть $0 < {{r}_{0}} \leqslant 1$. Тогда корни ${{\lambda }_{m}}(\varepsilon )$ вещественные и имеют место асимптотические равенства

Лемма 3. Пусть $1 < {{r}_{0}} \leqslant \frac{\pi }{2}$. Тогда корни ${{\lambda }_{m}}(\varepsilon )$ комплексные и имеют место асимптотические равенства

Итак, при сформулированных условиях определены значения параметров задачи, при которых реализуется критический случай и найдена асимптотика бесконечного множества таких корней характеристического уравнения, вещественные части которых стремятся к нулю при $\varepsilon \to 0$.

3. ПОСТРОЕНИЕ КВАЗИНОРМАЛЬНОЙ ФОРМЫ

Фиксируем ${{r}_{0}} \in \left( {0,\frac{\pi }{2}} \right]$. Для исследования асимптотики близких к состоянию равновесия ${{u}_{0}} = 1$ решений введем в рассмотрение формальный ряд

где $\tau = {{\varepsilon }^{2}}t$ – медленное время, $y = ({{z}_{0}}{{\varepsilon }^{{ - 1}}} + \theta )x$, $\xi (\tau ,x)$ – неизвестная комплекснозначная амплитуда, функции ${{u}_{j}}(t,\tau ,x,y)$ периодические по $t$, $x$ и $y$. Отметим, что второе слагаемое в правой части (15) основано на решении линеаризованного уравнения и имеет амплитуду $\xi (\tau ,x)$. Подставим (15) в (7) и будем последовательно приравнивать коэффициенты при одинаковых степенях $\varepsilon $. При первой степени $\varepsilon $ получаем верное равенство, а на следующем шаге находим, что

Собирая коэффициенты при ε³, получаем уравнение для ${{u}_{3}}$. Из условия его разрешимости в указанном классе функций приходим к краевой задаче относительно $\xi (\tau ,x)$:

а для ляпуновской величины δ имеет место формула

Квазинормальная форма (16) играет роль нормальной формы. Смысл этого термина раскрывает следующее утверждение. В нем через ${{\varepsilon }_{n}}({{\theta }_{0}})$ обозначается такая последовательность ${{\varepsilon }_{n}} \to 0$, что при всех $n$ имеем $\theta ({{\varepsilon }_{n}}({{\theta }_{0}})) = {{\theta }_{0}}$.

Теорема 1. Пусть ${{r}_{0}} \in \left( {0,\frac{\pi }{2}} \right]$ и ${{\theta }_{0}} \in [0,1)$. Пусть ${{\xi }_{0}}(\tau ,x)$ – ограниченное при $\tau \to \infty $, $x \in [0,2\pi ]$ решение краевой задачи (16) при $\theta = {{\theta }_{0}}$. Тогда при $\varepsilon = {{\varepsilon }_{n}}({{\theta }_{0}})$ функция

удовлетворяет краевой задаче (7), (6) с точностью до $O(\varepsilon _{n}^{3}({{\theta }_{0}}))$.

Отметим, что в том случае, когда ${{\xi }_{0}}(\tau ,x)$ – грубое периодическое по $\tau $ решение (16), можно обосновать результат о существовании точного почти периодического решения, близкого к (18), той же, что и ${{\xi }_{0}}(\tau ,x)$, устойчивости.

4. КВАЗИНОРМАЛЬНАЯ ФОРМА ПРИ $\sigma = \varepsilon {{\sigma }_{0}}$

Этот случай имеет особое значение, поскольку тогда выражение $\int\limits_{ - \infty }^\infty {F(s,\varepsilon )u(t,x + s)ds} $ в (17) близко к $u(t,x + \varepsilon ) - 2u(t,x) + u(t,x - \varepsilon )$ и для каждого z имеет место асимптотическое представление g(z) = = $1 - {\text{cos}}z \cdot (1 - {{\varepsilon }^{2}}\sigma _{0}^{2}{{z}^{2}} + o({{\varepsilon }^{4}}))$. Для $w(r)$ сохраняется выражение из раздела 2, а $d(r) = \frac{1}{2}{{({{r}^{2}} - {{\omega }^{2}}(r))}^{{\frac{1}{2}}}}$. Основное отличие здесь связано с тем, что значение ${{z}_{0}}$ определяется неоднозначно: ${{z}_{0}} = \pi + 2\pi n$, n = 0, ±1, ±2, ... Приведем итоговый результат.

Роль квазинормальной формы (16) играет краевая задача с двумя пространственными переменными для $\xi (\tau ,x,y)$:

Выражение (17) для коэффициента δ здесь упрощается, поскольку $g({{z}_{0}}) = 2$, $g{\kern 1pt} '{\kern 1pt} '({{z}_{0}}) = - 1$ и $g(2{{z}_{0}}) = 0$.

Решение $\xi (\tau ,x,y)$ связано с решением $u(t,x,\varepsilon )$ исходной краевой задачи (7), (6) формулой

$\tau = {{\varepsilon }^{2}}t$, $y = 2\pi {{\varepsilon }^{{ - 1}}}x$. Отметим, что в силу равенства (4) параметр $\theta $ в (19) отсутствует.

5. ВЫВОДЫ

Показано, что локальная динамика связанных логистических уравнений с запаздыванием при определенных условиях описывается решениями параболических уравнения типа Гинзбурга–Ландау. Получено асимптотическое представление решений при $t \in [{{t}_{0}},\infty )$, $x \in [0,2\pi ]$. Простейшие решения вида $\mathop {{\text{const}}}\nolimits_ \cdot \exp (i\omega t + ikx)$ таких уравнений оказываются неустойчивы. В ряде случаев в нормализованные уравнения входит параметр $\theta $ и при $\varepsilon \to 0$ могут происходить неограниченный процесс прямых и обратных бифуркаций. Особо отметим, что при $r < \frac{\pi }{2}$, т.е. в условии, когда в отсутствии связей нет колебаний в базовом уравнении (1), в связанной системе могут наблюдаться сложные неоднородные колебательные процессы. Особо отметим, что задача с антидиффузионной связью при сформулированных условиях редуцируется к нелинейной краевой задаче параболического типа.