1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 503, № 1, 2022

Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 503, № 1, стр. 87-90

СЛАБО СИНГУЛЯРНОЕ УСЛОВИЕ СТЕКЛОВА В МНОГОМЕРНОМ СЛУЧАЕ

А. Г. Чечкина 1, 2, *

1 Московский государственный университет имени М.В. Ломоносова
Москва, Россия

2 Институт математики с вычислительным центром УФИЦ РАН
Уфа, Башкортостан, Россия

* E-mail: chechkina@gmail.com

Поступила в редакцию 26.02.2021
После доработки 26.02.2021
Принята к публикации 08.02.2022

Полный текст (PDF)

Аннотация

В n-мерной ($n \geqslant 3$) области рассматривается задача типа Стеклова с быстро меняющимся условием (чередуются условие Стеклова и однородное условие Дирихле). При этом коэффициент в условии Стеклова является быстро осциллирующей функцией, зависящей от малого параметра $\varepsilon $, которая имеет порядок O(1) вне мелких включений в виде шаровых слоев на границе, где она имеет порядок $O({{(\varepsilon \delta )}^{{ - m}}})$. Эти включения диаметра $O(\varepsilon \delta )$ расположены на расстоянии порядка $O(\delta )$ друг от друга, где $\delta = \delta (\varepsilon ) \to 0$. В случае m < 2 (слабая сингулярность) оценена скорость сходимости решений исходной задачи при стремлении малого параметра к нулю.

Ключевые слова: слабая сингулярность, задача Стеклова, граничное усреднение

Сингулярные возмущения коэффициентов дифференциальных уравнений и краевых условий возникают при моделировании различных прикладных задач. Асимптотический анализ таких задач см., например, в работах [1–6]. Непериодические случаи рассмотрены в [7, 8]. Задачи с сингулярностями внутри области изучены в работах [9, 10] (см. также [11, 12]).

Задача типа Стеклова с быстро меняющимся типом краевых условий рассматривалась в [13], где проанализирован весь спектр предельных случаев. Задачи с быстро осциллирующими граничными условиями изучались также в статьях [14, 15].

В настоящей работе рассматривается многомерная задача усреднения типа Стеклова со слабой сингулярностью, даются в соболевских нормах оценки скорости сходимости решений и собственных значений исходных задач от решений и собственных значений, соответственно, усредненных задач при стремлении малого параметра к нулю.

ПОСТАНОВКА ЗАДАЧИ

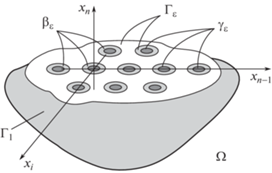
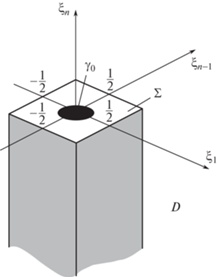
Рассмотрим область $\Omega \subset {{\mathbb{R}}^{n}}$, $n \geqslant 3$, с достаточно гладкой границей $\partial \Omega $. Мы предполагаем, что часть границы ${{\Gamma }_{2}}$ ($\partial \Omega = {{\Gamma }_{1}} \cup {{\Gamma }_{2}}$) лежит на гиперплоскости ${{x}_{n}} = 0$, при этом она состоит из трех частей ${{\alpha }_{\varepsilon }}$, ${{\beta }_{\varepsilon }}$ и ${{\gamma }_{\varepsilon }}$, где ${{\alpha }_{\varepsilon }}$ и ${{\beta }_{\varepsilon }}$ образуют единую часть, которую мы обозначаем ${{\Gamma }_{\varepsilon }}$. Здесь ${{\gamma }_{\varepsilon }} = \bigcup\limits_{i = 1}^{{{N}_{\delta }}} {\gamma _{\varepsilon }^{i}} $ – объединение (n – 1)-мерных шаров, а ${{\beta }_{\varepsilon }} = \bigcup\limits_{i = 1}^{{{N}_{\delta }}} {\beta _{\varepsilon }^{i}} $ – объединение шаровых слоев. Поясним теперь построение. Пусть γ0 – это (n – 1)-мерный шар $\{ ({{\xi }_{1}},\; \ldots ,\;{{\xi }_{n}})|\xi _{1}^{2} + \; \ldots \; + \xi _{{n - 1}}^{2} < {{\varepsilon }^{2}},\;{{\xi }_{n}} = 0\} $ и пусть β0 = = $\{ ({{\xi }_{1}},\; \ldots ,\;{{\xi }_{n}})|{{\varepsilon }^{2}} < \xi _{1}^{2} + \; \ldots \; + \xi _{{n - 1}}^{2} < 2{{\varepsilon }^{2}}$, ξn = 0} в растянутом пространстве ${{\mathbb{R}}^{n}}$, $\xi \frac{x}{\delta }$, $\gamma $ и $\beta $ – области, полученные целочисленными сдвигами множеств γ0 и ${{\beta }_{0}}$ на гиперплоскости $\{ {{\xi }_{n}} = 0\} $ с центрами в точках ${{\widetilde \xi }_{k}} = ({{k}_{1}},\; \ldots ,\;{{k}_{{n - 1}}},0)$, ${{k}_{1}},\; \ldots ,\;{{k}_{{n - 1}}} \in \mathbb{N}$. Обозначим ${{\tilde {\gamma }}_{\varepsilon }}$ – гомотетичное сжатие δγ и ${{\widetilde \beta }_{\varepsilon }}$ – гомотетичное сжатие $\delta \beta $. При этом (см. рис. 1)

${{\gamma }_{\varepsilon }} = {{\tilde {\gamma }}_{\varepsilon }} \cap \partial \Omega ,\quad {{\beta }_{\varepsilon }} = {{\widetilde \beta }_{\varepsilon }} \cap \partial \Omega \quad {{\alpha }_{\varepsilon }} = {{\Gamma }_{2}}{{\backslash }}({{\beta }_{\varepsilon }} \cup {{\gamma }_{\varepsilon }}).$
Рис. 1.

Область с микронеоднородной структурой границы.

Предполагается, что параметр δ(ε), определяющий характерное расстояние между участками $\gamma _{\varepsilon }^{i}$ и $\beta _{\varepsilon }^{i}$ на границе, стремится к нулю при $\varepsilon \to 0$. Также заметим, что количество участков $\beta _{\varepsilon }^{i}$ и соответственно участков $\gamma _{\varepsilon }^{i}$ имеет следующий порядок: ${{N}_{\delta }} = O\left( {\frac{1}{{{{\delta }^{{n - 1}}}}}} \right)$.

В области $\Omega $ рассматривается спектральная задача с быстрой сменой краевых условий и сингулярными коэффициентами

(1)
$\begin{gathered} \Delta u_{\varepsilon }^{k} = 0\quad {\text{в}}\quad \Omega , \\ u_{\varepsilon }^{k} = 0\quad {\text{на}}\quad {{\Gamma }_{1}} \cup {{\gamma }_{\varepsilon }}, \\ \frac{{\partial u_{\varepsilon }^{k}}}{{\partial {{x}_{n}}}} = \lambda _{\varepsilon }^{k}{{\rho }^{\varepsilon }}(x)u_{\varepsilon }^{k}\quad {\text{на}}\quad {{\Gamma }_{\varepsilon }}, \\ \end{gathered} $
где

(2)
${{\rho }^{\varepsilon }}(x) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{{{(\varepsilon \delta )}}^{m}}}},\quad x \in {{\beta }_{\varepsilon }},} \\ {1,\quad x \in {{\alpha }_{\varepsilon }}.} \end{array}} \right.$

В этой работе ограничимся только случаем m < 2 (слабая сингулярность).

Собственные значения $\{ \lambda _{\varepsilon }^{k}\} $ занумерованы в порядке неубывания, т.е. $\lambda _{\varepsilon }^{1} \leqslant \lambda _{\varepsilon }^{2} \leqslant \; \cdots \; \leqslant \lambda _{\varepsilon }^{k} \leqslant \; \cdots $, и повторяются с учетом кратности. При этом нормируем собственные функции следующим образом:

$\int\limits_{{{\Gamma }_{2}}} {{{\rho }^{\varepsilon }}} (\hat {x},0)u_{\varepsilon }^{k}(\hat {x},0)u_{\varepsilon }^{l}(\hat {x},0)d\hat {x} = {{\delta }_{{kl}}},$
здесь $\hat {x} = ({{x}_{1}},\; \ldots ,\;{{x}_{{n - 1}}})$.

Для формулировки теорем нам понадобится величина

$P: = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{{{\varepsilon }^{{n - 2}}}}}{{\delta (\varepsilon )}}.$

Обозначим

$D = \left\{ {\xi \in {{\mathbb{R}}^{n}}| - \frac{1}{2} < {{\xi }_{i}} < \frac{1}{2},i = 1,\; \ldots \;n - 1,{{\xi }_{n}} < 0} \right\},$
$\Sigma = \left\{ {\xi \in {{\mathbb{R}}^{n}}| - \frac{1}{2} < {{\xi }_{i}} < \frac{1}{2},i = 1,\; \ldots ,\;n - 1,{{\xi }_{n}} = 0} \right\}.$

Пусть функция Wε, периодическая по переменным ${{\xi }_{1}},\; \ldots ,\;{{\xi }_{{n - 1}}}$, является первой собственной функцией задачи типа Стеклова на ячейке периодичности

(3)
$\begin{gathered} \Delta {{W}^{\varepsilon }} = 0\quad {\text{в}}\quad D, \\ {{W}^{\varepsilon }} = 0\quad {\text{на}}\quad {{\gamma }_{0}} \\ \frac{{\partial {{W}^{\varepsilon }}}}{{\partial {{\xi }_{n}}}} = {{\theta }_{\varepsilon }}{{W}^{\varepsilon }}\quad {\text{на}}\quad \Sigma {{\backslash }}{{\gamma }_{0}}. \\ \end{gathered} $

Зададим $w_{\varepsilon }^{\delta }$ формулой

(4)
$w_{\varepsilon }^{\delta }(x) = 1 + \psi ({{x}_{n}})\left( {{{W}^{\varepsilon }}\left( {\frac{x}{\delta }} \right) - 1} \right)$
и продолжим ее периодически вдоль гиперплоскости xn = 0. Здесь $\psi (t)$ – гладкая срезающая функция одной переменной, $0 \leqslant \psi \leqslant 1$, $\psi \equiv 1$ в некоторой достаточно малой окрестности ${{\Gamma }_{2}}$. Свойства функции $w_{\varepsilon }^{\delta }$ подробно изучены в [13].

Для формулировки результатов рассмотрим краевые задачи

(5)
$\begin{gathered} \Delta {{u}^{\varepsilon }} = 0\quad {\text{в}}\quad \Omega , \\ {{u}^{\varepsilon }} = 0\quad {\text{на}}\quad {{\Gamma }_{1}} \cup {{\gamma }_{\varepsilon }}, \\ \frac{{\partial {{u}^{\varepsilon }}}}{{\partial {{x}_{n}}}} = {{\rho }^{\varepsilon }}(x)f(x)\quad {\text{на}}\quad {{\Gamma }_{\varepsilon }}. \\ \end{gathered} $
(6)
$\begin{gathered} \Delta {{u}^{0}} = 0\quad {\text{в}}\quad \Omega , \\ {{u}^{0}} = 0\quad {\text{на}}\quad \partial \Omega ,\quad (P = + \infty ), \\ \left[ \begin{gathered} \frac{{\partial {{u}^{0}}}}{{\partial {{x}_{n}}}} + P\frac{{{{\sigma }_{n}}{{c}_{{{{\gamma }_{0}}}}}}}{2}{{u}^{0}} = f(x)\quad {\text{на}}\quad {{\Gamma }_{2}} \\ {{u}^{0}} = 0\quad {\text{на}}\quad {{\Gamma }_{1}} \\ \end{gathered} \right],\quad (P < + \infty ), \\ \end{gathered} $
где ${{\sigma }_{n}}$ – площадь единичной n-мерной сферы, а ${{c}_{{{{\gamma }_{0}}}}}: = {\text{cap}}({{\gamma }_{0}})$ – гармоническая емкость (n – 1)-мерного диска γ0.

Имеет место теорема об оценке решений.

Теорема 1. Если $P < + \infty $, ${{u}^{\varepsilon }}$ и u0– обобщенные решения задач (4) и (5), соответственно, то существует такая константа ${{K}_{1}}(f,{{\gamma }_{0}},n)$, не зависящая от $\varepsilon $ и $\delta $, что для достаточно малых ε имеем

${\text{||}}{{u}^{0}}w_{\varepsilon }^{\delta } - {{u}^{\varepsilon }}{\text{|}}{{{\text{|}}}_{{{{H}^{1}}(\Omega )}}} \leqslant {{K}_{1}}\left( {{{\varepsilon }^{{\tfrac{{n - 2}}{2}}}} + \left| {\frac{{{{\varepsilon }^{{n - 2}}}}}{\delta } - P} \right| + {{\varepsilon }^{{2 - m}}}{{\delta }^{{2 - m}}}} \right).$

Если $P = + \infty $, то существует ${{K}_{2}}(f,{{\gamma }_{0}},n)$ такое, что

${{\left\| {{{u}^{\varepsilon }}} \right\|}_{{{{L}_{2}}(\Omega )}}} \leqslant {{K}_{2}}\left( {\frac{{{{\delta }^{{\tfrac{1}{2}}}}}}{{{{\varepsilon }^{{\tfrac{{n - 2}}{2}}}}}} + {{\varepsilon }^{{2 - m}}}{{\delta }^{{2 - m}}}} \right).$

Теперь сформулируем спектральную задачу

(7)
$\begin{gathered} \Delta u_{0}^{k} = 0\quad {\text{в}}\quad \Omega , \\ u_{0}^{k} = 0\quad {\text{на}}\quad \partial \Omega \quad (P = + \infty ), \\ \left[ \begin{gathered} \frac{{\partial u_{0}^{k}}}{{\partial {{x}_{n}}}} + P\frac{{{{\sigma }_{n}}{{c}_{{{{\gamma }_{0}}}}}}}{2}u_{0}^{k} = \lambda _{0}^{k}u_{0}^{k}\quad {\text{на}}\quad {{\Gamma }_{2}}, \\ u_{0}^{k} = 0\quad {\text{на}}\quad {{\Gamma }_{1}}, \\ \int\limits_{{{\Gamma }_{2}}} {u_{0}^{k}} u_{0}^{l}d\widehat x = {{\delta }_{{kl}}},\quad 0 < \lambda _{0}^{1} \leqslant \lambda _{0}^{2} \leqslant \; \cdots \\ \end{gathered} \right]\quad (P < + \infty ). \\ \end{gathered} $

Имеет место теорема о сходимости собственных значений и собственных функций.

Теорема 2. Пусть $\lambda _{0}^{k}$, $\lambda _{\varepsilon }^{k}$ являются собственными значениями задач (6) и (1) соответственно. Тогда

$\begin{gathered} \left| {\lambda _{0}^{k} - \lambda _{\varepsilon }^{k}} \right| \leqslant C_{k}^{1}\left( {{{\varepsilon }^{{\tfrac{{n - 2}}{2}}}} + \left| {\frac{{{{\varepsilon }^{{n - 2}}}}}{\delta } - P} \right| + {{\varepsilon }^{{2 - m}}}{{\delta }^{{2 - m}}}} \right), \\ {\text{если}}\quad P < \infty , \\ \end{gathered} $
$\lambda _{\varepsilon }^{k} \to + \infty \quad {\text{при}}\quad \varepsilon \to 0,\quad {\text{если}}\quad P = + \infty ,$
где постоянные $C_{k}^{1}$, $C_{k}^{2}$ не зависят от ε.

Рис. 2.

Ячейка периодичности.

Если кратность собственного значения $\lambda _{0}^{l}$ задачи (7) равна r, т.е. $\lambda _{0}^{l} = \lambda _{0}^{{l + 1}} = \; \cdots \; = \lambda _{0}^{{l + r}}$, то для любой собственной функции $u_{0}^{l}$ задачи (7), соответствующей собственному значению $\lambda _{0}^{l}$, ${{\left\| {{{u}_{0}}} \right\|}_{{{{L}_{2}}(\Omega )}}} = 1$, существует линейная комбинация ${{\bar {u}}^{\varepsilon }}$ собственных функций задачи (1), соответствующих собственному значению $\lambda _{\varepsilon }^{{l + 1}},\; \cdots \;,\lambda _{\varepsilon }^{{l + r}}$ такая, что

$\begin{gathered} {{\left\| {{{u}^{\varepsilon }} - u_{0}^{l}} \right\|}_{{{{L}_{2}}(\Omega )}}} \leqslant \\ \leqslant \;C_{l}^{1}\left( {{{\varepsilon }^{{\tfrac{{n - 2}}{2}}}} + \left| {\frac{{{{\varepsilon }^{{n - 2}}}}}{\delta } - P} \right| + {{\varepsilon }^{{2 - m}}}{{\delta }^{{2 - m}}}} \right),\quad {\text{если}}\quad P < \infty , \\ \end{gathered} $
${{\left\| {{{u}^{\varepsilon }}} \right\|}_{{{{L}_{2}}(\Omega )}}} \leqslant C_{l}^{2}\left( {\frac{{{{\delta }^{{\tfrac{1}{2}}}}}}{{{{\varepsilon }^{{\tfrac{{n - 2}}{2}}}}}} + {{\varepsilon }^{{2 - m}}}{{\delta }^{{2 - m}}}} \right),\quad {\text{если}}\quad P = + \infty ,$
где постоянные $C_{l}^{1}$, $C_{l}^{2}$ не зависят от ε и $u_{0}^{l}$.

Список литературы

  1. Головатый Ю.Д., Назаров С.А., Олейник О.А., Соболева Т.С. О собственных колебаниях струны с присоединенной массой // Сиб. мат. журнал. 1988. Т. 29. № 5. С. 71–91.

  2. Gómez D., Lobo M., Pérez E. On the Eigenfunctions Associated with the High Frequencies in Systems with a Concentrated Mass // J. Math. Pures Appl. 1999. V. 78. P. 841–865.

  3. Sanchez-Hubert J., Sanchez-Palencia É. Vibration and Coupling of Continuous System. Asymptotic methods. Berlin–Heidelberg: Springer-Verlag, 1989. 421 p.

  4. Chechkin G.A. On Vibration of Partially Fastened Membrane with Many “Light” Concentrated Masses on the Boundary // C. R. Mмanique. 2004. V. 332. № 12. P. 949–954.

  5. Чечкин Г.А. Расщепление кратного собственного значения в задаче о концентрированных массах // Успехи мат. наук. 2004. Т. 59. Вып. 4. С. 205–206.

  6. Rybalko V. Vibration of Elastic Systems with a Large Number of Tiny Heavy Inclusions // Asymptotic Analysis. 2002. V. 32. № 1. P. 27–62.

  7. Перес М.Е., Чечкин Г.А., Яблокова (Доронина) Е.И. О собственных колебаниях тела с “легкими” концентрированными массами на поверхности // Успехи мат. наук. 2002. Т. 57. Вып. 6. С. 195–196.

  8. Chechkin G.A., Chechkina T.P. Random Homogenization in a Domain with Light Concentrated Masses // Mathematics. 2020. V. 8. № 5. https://doi.org/10.3390/math8050788

  9. Chechkin G.A., Mel’nyk T.A. Asymptotics of Eigenelements to Spectral Problem in Thick Cascade Junction with Concentrated Masses // Applicable Analysis. 2012. V. 91. № 6. P. 1055–1095.

  10. Chechkin G.A., Mel’nyk T.A. Spatial–Skin Effect for Eigenvibrations of a Thick Cascade Junction with “Heavy” Concentrated Masses // Mathematical Methods in Applied Sciences (M2AS). 2014. V. 37, № 1. P. 56–74.

  11. Amirat Y., Chechkin G.A., Gadyl’shin R.R. Asymptotics of the Solution of a Dirichlet Spectral Problem in a Junction with Highly Oscillating Boundary // C. R. Mécanique. 2008. V. 336. № 9. P. 693–698.

  12. Chechkin G.A., Cioranescu D., Damlamian A., Piatnitski A.L. On Boundary Value Problem with Singular Inhomogeneity Concentrated on the Boundary // Journal de Mathématiques Pures et Appliquos. 2012. V. 98. № 2. P. 115–138.

  13. Чечкина А.Г. Усреднение спектральных задач с сингулярным возмущением условия Стеклова // Известия РАН. 2017. Т. 81. № 1. С. 203–240.

  14. Гадыльшин Р.Р., Чечкин Г.А. Краевая задача для Лапласиана с быстро меняющимся типом граничных условий в многомерной области // Сиб. мат. журнал. 1999. Т. 40. № 2. С. 271–287.

  15. Oleinik O.A., Chechkin G.A. Solutions and Eigenvalues of the Boundary Value Problems with Rapidly Alternating Boundary Conditions for the System of Elasticity // Rendiconti Lincei: Mathematica e Applicazioni. Serie 9. 1996. V. 7. № 1. P. 5–15.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал