1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 503, № 1, 2022

Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 503, № 1, стр. 59-63

О ЗАДАЧЕ СТЕФАНА ДЛЯ СИСТЕМЫ УРАВНЕНИЙ МАГНИТОГИДРОДИНАМИЧЕСКОГО ПОГРАНИЧНОГО СЛОЯ С ИНЪЕКЦИЕЙ СРЕДЫ С РЕОЛОГИЧЕСКИМ ЗАКОНОМ О. А. ЛАДЫЖЕНСКОЙ

М. А. Кисатов 1, *

1 Московский государственный университет имени М.В. Ломоносова
Москва, Россия

* E-mail: kisatov@mail.ru

Поступила в редакцию 19.10.2021
После доработки 19.10.2021
Принята к публикации 08.02.2022

Полный текст (PDF)

Аннотация

Работа посвящена теореме существования единственного классического решения задачи Стефана, возникающей при изучении магнитогидродинамического пограничного слоя в вязкой среде с инъекцией модифицированной среды с реологическим законом О.А. Ладыженской.

Ключевые слова: пограничный слой жидкости, вязкая среда, реологический закон О.А. Ладыженской, задача Стефана, задача дифракции пограничного слоя

Изучение задач в областях с подвижными границами является важным направлением в теории дифференциальных уравнений с частными производными, при этом важность изучения этих задач также подчеркивается и многочисленными приложениями. О задачах Стефана см. работы [1, 2], а также литературу в этих работах.

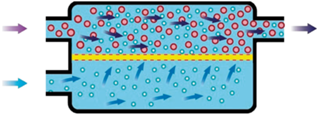
В настоящей работе рассматривается задача Стефана, возникающая в теории магнитогидродинамического пограничного слоя реологически сложных сред. Предполагается, что жидкость с определенными свойствами обтекает пористую поверхность, через которую происходит инъекция жидкости с иными электромагнитными и реологическими свойствами (см. рис. 1). При этом жидкости не смешиваются и их разделяет некоторая поверхность, на которой возникают условия сопряжения параметров, определяющих жидкости. Эта поверхность находится в движении. Обоснование актуальности подобных задач с физической точки зрения можно найти, к примеру, в работе [3]. Похожая задача магнитогидродинамического пограничного слоя с условиями дифракции для двух жидкостей с различными реологическими свойствами была рассмотрена в работе [4]. В работе [5] рассматривалась задача дифракции с инъекцией дилатантной среды в пограничный слой (о дилатантной среде см. также [6]).

Рис. 1.

Инъекция жидкости через мембрану.

Слоистые неньютоновские жидкие среды рассматривались в работах [7–9]. Неоднородные неньютоновские жидкости изучались также в [10]. Модификация О.А. Ладыженской пограничного слоя неньютоновской жидкости изучена в работе [11]. Магнитная среда с реологическим законом О.А. Ладыженской исследовалась в [12], а аналогичная дилатантная жидкость рассматривалась в [13].

1. ПОСТАНОВКА ЗАДАЧИ И ФОРМУЛИРОВКА ОСНОВНОГО РЕЗУЛЬТАТА

В области $D = \{ 0 < x < X,\;0 < y < \infty \} $, разделенной непрерывной кривой γ = {(x, y): y = = ${{y}_{*}}(x)\, > \,0,0 \leqslant x \leqslant X\} $ на области

$\begin{gathered} {{D}_{1}} = \{ 0 < x < X,\;0 < y < {{y}_{*}}(x)\} \quad {\text{и}} \\ {{D}_{2}} = \{ 0 < x < X,\;{{y}_{*}}(x) < y < \infty \} , \\ \end{gathered} $
рассматривается краевая задача для уравнений пограничного слоя. В области D1 рассматривается система уравнений
(1)
$\begin{gathered} {{u}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial x}} + {{{v}}_{1}}\frac{{\partial {{u}_{1}}}}{{\partial y}} = {{\nu }_{1}}\left( {1 + 3k{{{\left( {\frac{{\partial {{u}_{1}}}}{{\partial y}}} \right)}}^{2}}} \right)\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{y}^{2}}}} - \frac{1}{{{{\rho }_{1}}}}\frac{{dp(x)}}{{dx}} - \\ - \frac{{{{\sigma }_{1}}}}{{{{\rho }_{1}}}}B(x)({{u}_{1}}B(x) + E(x)), \\ \frac{{\partial {{u}_{1}}}}{{\partial x}} + \frac{{\partial {{{v}}_{1}}}}{{\partial y}} = 0, \\ \end{gathered} $
модифицированной электропроводной среды с реологическим законом О.А. Ладыженской, а в области D2 – система уравнений
(2)
$\begin{gathered} {{u}_{2}}\frac{{\partial {{u}_{2}}}}{{\partial x}} + {{{v}}_{2}}\frac{{\partial {{u}_{2}}}}{{\partial y}} = {{\nu }_{2}}\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{y}^{2}}}} - \frac{1}{{{{\rho }_{2}}}}\frac{{dp(x)}}{{dx}} - \\ - \frac{{{{\sigma }_{2}}}}{{{{\rho }_{2}}}}B(x)({{u}_{2}}B(x) + E(x)), \\ \frac{{\partial {{u}_{2}}}}{{\partial x}} + \frac{{\partial {{{v}}_{2}}}}{{\partial y}} = 0. \\ \end{gathered} $
ньютоновской электропроводной среды.

В уравнениях k – малая положительная постоянная, ${{\nu }_{1}} > 0$, ${{\nu }_{2}}$ – вязкость соответствующей жидкости, ${{\rho }_{1}} > 0$, ${{\rho }_{2}} > 0$ – плотность среды, ${{\sigma }_{1}}$ > 0, ${{\sigma }_{2}} > 0$ – соответствующая электропроводность, B(x) – y-компонента вектора магнитной индукции, $E(x)$ – компонента вектора напряженности электрического поля, ортогональная плоскости XOY, $p(x)$ – давление.

Соответствующие граничные условия имеют вид

(3)
$\begin{array}{*{20}{l}} \begin{gathered} {{u}_{1}}(0,y) = {{u}_{{10}}}(y)\;\;{\text{при}}\;\;0 \leqslant y \leqslant {{y}_{*}}(0); \\ {{u}_{1}}(x,0) = 0,\quad {{{v}}_{1}}(x,0) = {{{v}}_{0}}(x), \\ \end{gathered} \\ \begin{gathered} {{u}_{2}}(0,y) = {{u}_{{20}}}(y)\;\;{\text{при}}\;\;{{y}_{*}}(0) \leqslant y < \infty ; \\ {{u}_{2}}(x,y) \to U(x)\;\;{\text{при}}\;\;y \to \infty , \\ \end{gathered} \end{array}$
где значение ${{y}_{*}}(0)$ и функции ${{u}_{{10}}}(y)$, ${{u}_{{20}}}(y)$, ${{{v}}_{0}}(x)$, $U(x)$ > 0 считаются заданными, причем ${{u}_{{i0}}}(y)\, \leqslant \,U(0)$, i = 1, 2. Зададим на кривой $\gamma $ условия сопряжения:

(4)
${{u}_{1}}(x,{{y}_{*}}(x)) = {{u}_{2}}(x,{{y}_{*}}(x)),$
(5)
$\begin{gathered} {{\nu }_{1}}{{\rho }_{1}}\frac{{\partial {{u}_{1}}(x,{{y}_{*}}(x))}}{{\partial y}}\left( {1 + k{{{\left( {\frac{{\partial {{u}_{1}}(x,{{y}_{*}}(x))}}{{\partial y}}} \right)}}^{2}}} \right) = \\ = \;{{\nu }_{2}}{{\rho }_{2}}\frac{{\partial {{u}_{2}}(x,{{y}_{*}}(x))}}{{\partial y}}. \\ \end{gathered} $

Кривую γ будем считать гладкой линией тока. В силу этого выполнено

(6)
$\frac{{d{{y}_{*}}(x)}}{{dx}} = \frac{{{{{v}}_{1}}(x,{{y}_{*}}(x))}}{{{{u}_{1}}(x,{{y}_{*}}(x))}} = \frac{{{{{v}}_{2}}(x,{{y}_{*}}(x))}}{{{{u}_{2}}(x,{{y}_{*}}(x))}}.$

В задаче (1)–(6) неизвестными являются функции ${{u}_{i}}(x,y)$, ${{{v}}_{i}}(x,y)$, ${{y}_{*}}(x)$, i = 1, 2. Поскольку граница γ является неизвестной, то рассматриваемая задача является задачей типа Стефана.

Давление p(x) можно исключить из уравнений, выразив через скорость внешнего потока $U(x)$ > 0, используя соотношение

$ - \frac{{dp(x)}}{{dx}} - {{\sigma }_{2}}B(x)E(x)\, = \,{{\rho }_{2}}U(x)\frac{{dU(x)}}{{dx}}\, + \,{{\sigma }_{2}}{{B}^{2}}(x)U(x).$

Введем новые обозначения

$\begin{gathered} {{u}_{0}}(y) = \left( {\begin{array}{*{20}{c}} {{{u}_{{10}}}(y),}&{0 \leqslant y \leqslant {{y}_{*}}(0),} \\ {{{u}_{{20}}}(y),}&{{{y}_{*}}(0) < y < \infty ,} \end{array}} \right. \\ \nu (y) = \left( {\begin{array}{*{20}{c}} {{{\nu }_{1}},}&{0 < y \leqslant {{y}_{*}}(x),} \\ {{{\nu }_{2}},}&{{{y}_{*}}(x) < y < \infty ,} \end{array}} \right. \\ \end{gathered} $
$\begin{gathered} u(x,y) = \left( {\begin{array}{*{20}{c}} {{{u}_{1}}(x,y),}&{(x,y) \in {{D}_{1}},} \\ {{{u}_{2}}(x,y),}&{(x,y) \in {{D}_{2}},} \end{array}} \right. \\ {v}(x,y) = \left( {\begin{array}{*{20}{c}} {{{{v}}_{1}}(x,y),}&{(x,y) \in {{D}_{1}},} \\ {{{{v}}_{2}}(x,y),}&{(x,y) \in {{D}_{2}},} \end{array}} \right. \\ \end{gathered} $
и приведем определение обобщенного решения задачи (1)–(6).

Определение 1. Обобщенным решением задачи (1)–(6) в области D называются функции $u(x,y)$, ${v}(x,y)$, ${{y}_{*}}(x)$, $(x,y) \in D$, удовлетворяющие следующим условиям:

1) $u(x,y)$ положительна при $y > 0$, непрерывна в замкнутой области $\bar {D}$, ограничена; ${v}(x,y)$ принадлежит пространству $L_{2}^{{loc}}(D)$ и непрерывна по y при y =0;

2) существуют обобщенные производные $\frac{{\partial u}}{{\partial x}}$, $\frac{{\partial u}}{{\partial y}}$, $\frac{{\partial {v}}}{{\partial y}}$, производная $\frac{{\partial u}}{{\partial y}}$ ограничена, производные $\frac{{\partial u}}{{\partial x}}$ и $\frac{{\partial {v}}}{{\partial y}}$ принадлежат пространству $L_{2}^{{loc}}(D)$;

3) $u(0,y) = {{u}_{0}}(y)$, $u(x,0) = 0$, $u(x,y) \to U(x)$ при $y \to \infty $, ${v}(x,0) = {{{v}}_{0}}(x)$;

4) для любой непрерывной функции $\varphi (x,y)$, имеющей непрерывную производную $\frac{{\partial \varphi (x,y)}}{{\partial y}}$ и равной нулю при y = 0 и при достаточно больших y, функции $u(x,y)$ и ${v}(x,y)$ удовлетворяют интегральному тождеству

$\begin{gathered} \iint\limits_D \left[ {\left( {u\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial y}} + \frac{1}{{\rho (x,y)}}\frac{{dp(x)}}{{dx}} + } \right.} \right. \\ \left. { + \frac{{\sigma (x,y)}}{{\rho (x,y)}}B(x)(uB(x) + E(x))} \right)\varphi + \\ \end{gathered} $
$\left. { + \,\nu (y)\left( {1 + k{{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}}^{2}}} \right)\frac{{\partial u}}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}}} \right]dxdy = 0,$
где $\rho (x,y) \equiv {{\rho }_{i}}$, $\sigma (x,y) \equiv {{\sigma }_{i}}$ при $(x,y) \in {{D}_{i}}$, i = 1, 2;

5) справедливо равенство

$\frac{{d{{y}_{*}}(x)}}{{dx}} = \frac{{{v}(x,{{y}_{*}}(x))}}{{u(x,{{y}_{*}}(x))}};$

6) почти всюду в области D выполняется равенство

$\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} = 0.$

Основным результатом работы является следующее утверждение.

Теорема 1. Предположим, что функции $p{\text{'}}(x)$, ${{{v}}_{0}}(x)$, $B(x)$, $E(x)$ непрерывно дифференцируемы на отрезке $0 \leqslant x \leqslant X$, ${{u}_{{i0}}}(y)$, $u_{{i0}}^{'}(y)$, $u{{_{{i0}}^{{''}}}_{{}}}(y)$, i = 1, 2, ограничены и удовлетворяют условию Гёльдера, $u_{{10}}^{'}(0) > 0$, ${{u}_{{20}}}(y) \to U(0)$ при $y \to \infty $, ${{u}_{{i0}}}(y) \leqslant U(0)$, i = 1, 2, выполняются равенства

$\begin{gathered} {{u}_{{10}}}({{y}_{*}}(0)) = {{u}_{{20}}}({{y}_{*}}(0)), \\ {{\nu }_{1}}{{\rho }_{1}}u_{{10}}^{'}({{y}_{*}}(0))(1 + k{{(u_{{10}}^{'}({{y}_{*}}(0)))}^{2}}) = {{\nu }_{2}}{{\rho }_{2}}u_{{20}}^{'}({{y}_{*}}(0)) \\ \end{gathered} $
и условие согласования в точке (0, 0)

$\begin{gathered} {{\nu }_{1}}\left( {1 + \frac{3}{4}k{{{(u_{{10}}^{'}(y))}}^{2}}} \right)u_{{10}}^{{''}}(y) - {{{v}}_{0}}(0)u_{{10}}^{'}(y) - \\ - \frac{{p{\kern 1pt} '(0)}}{{{{\rho }_{1}}}} - \frac{{{{\sigma }_{1}}}}{{{{\rho }_{1}}}}{{B}^{2}}(0){{u}_{{10}}}(y) - \\ - \frac{{{{\sigma }_{1}}}}{{{{\rho }_{1}}}}B(0)E(0) = O({{y}^{2}})\quad при\quad y \to 0. \\ \end{gathered} $

Тогда при некотором X > 0 существует обобщенное решение задачи (1)–(6). Если, кроме того, выполняется неравенство

$\frac{{dp(x)}}{{dx}} + {{\sigma }_{i}}B(x)E(x) \leqslant - {{\beta }_{0}} < 0,$
где ${{\beta }_{0}} = {\text{const}}$, то решение существует при любом X > 0. Если же выполнены условия
$\frac{{dp(x)}}{{dx}} + {{\sigma }_{i}}B(x)E(x) \leqslant 0,\quad {{{v}}_{0}}(x) \geqslant 0,$
то решение задачи (1)–(6) единственно.

2. ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ

Для доказательства основного результата введем замену фон Мизеса

$x = x,\quad \psi = \psi (x,y),$
$\begin{gathered} \frac{{\partial \psi }}{{\partial y}} = u(x,y), \\ \frac{{\partial \psi }}{{\partial x}} = {{{v}}_{0}}(x) - {v}(x,y),\quad \psi (x,0) = 0, \\ \end{gathered} $
${{w}_{i}}(x,\psi ) = u_{i}^{2}(x,y),\quad i = 1,\;2,$
при которой системы уравнений (1), (2) преобразуются в квазилинейные уравнения
(7)
$\begin{array}{*{20}{l}} \begin{gathered} {{\nu }_{1}}\left( {1 + \frac{3}{4}k{{{\left( {\frac{{\partial {{w}_{1}}}}{{\partial \psi }}} \right)}}^{2}}} \right)\sqrt {{{w}_{1}}} \frac{{{{\partial }^{2}}{{w}_{1}}}}{{\partial {{\psi }^{2}}}} - \\ - \;\frac{{\partial {{w}_{1}}}}{{\partial x}} - {{{v}}_{0}}(x)\frac{{\partial {{w}_{1}}}}{{\partial \psi }} - \frac{{2{{\sigma }_{1}}{{B}^{2}}(x)}}{{{{\rho }_{1}}}}\sqrt {{{w}_{1}}} - \\ \end{gathered} \\ { - \;\frac{2}{{{{\rho }_{1}}}}\left( {\frac{{dp(x)}}{{dx}} + {{\sigma }_{1}}B(x)E(x)} \right) = 0} \end{array}$
в области ${{\Omega }_{1}} = \{ 0 < x < X,\;0 < \psi < {{\psi }_{*}}(x)\} $ и
(8)
$\begin{gathered} {{\nu }_{2}}\sqrt {{{w}_{2}}} \frac{{{{\partial }^{2}}{{w}_{2}}}}{{\partial {{\psi }^{2}}}} - \frac{{\partial {{w}_{2}}}}{{\partial x}} - {{{v}}_{0}}(x)\frac{{\partial {{w}_{2}}}}{{\partial \psi }} - \frac{{2{{\sigma }_{2}}{{B}^{2}}(x)}}{{{{\rho }_{2}}}}\sqrt {{{w}_{2}}} - \\ - \;\frac{2}{{{{\rho }_{2}}}}\left( {\frac{{dp(x)}}{{dx}} + {{\sigma }_{2}}B(x)E(x)} \right) = 0 \\ \end{gathered} $
в области ${{\Omega }_{2}} = \{ 0 < x < X,\;{{\psi }_{*}}(x) < \psi < \infty \} $. Граничные условия (3) переходят в условия
(9)
$\begin{gathered} {{w}_{1}}(0,\psi ) = {{w}_{{10}}}(\psi ),\quad 0 \leqslant \psi \leqslant {{\psi }_{*}}(0); \\ {{w}_{1}}(x,0) = 0,\quad {{w}_{2}}(0,\psi ) = {{w}_{{20}}}(\psi ), \\ {{\psi }_{*}}(0) \leqslant \psi < \infty , \\ {{w}_{2}}(x,\psi ) \to {{U}^{2}}(x)\quad {\text{при}}\quad \psi \to \infty , \\ \end{gathered} $
условия сопряжения (4), (5) переходят при $\psi = {{\psi }_{*}}(x)$, $0 \leqslant x \leqslant X$ в условия
(10)
$\begin{gathered} {{w}_{1}}(x,{{\psi }_{*}}(x)) = {{w}_{2}}(x,{{\psi }_{*}}(x)), \\ {{\nu }_{1}}{{\rho }_{1}}\frac{{\partial {{w}_{1}}(x,{{y}_{*}}(x))}}{{\partial \psi }}\left( {1 + \frac{k}{4}{{{\left( {\frac{{\partial {{w}_{1}}(x,{{\psi }_{*}}(x))}}{{\partial \psi }}} \right)}}^{2}}} \right) = \\ = \;{{\nu }_{2}}{{\rho }_{2}}\frac{{\partial {{w}_{2}}(x,{{\psi }_{*}}(x))}}{{\partial \psi }}, \\ \end{gathered} $
а неизвестная граница γ – в известную границу
$\Gamma = \{ (x,y){\text{:}}\;\psi = {{\psi }_{*}}(x) \equiv \psi (x,{{y}_{*}}(x)),\;0 \leqslant x \leqslant X\} ,$
где функция ${{\psi }_{*}}(x)$ находится из соотношений

$\begin{gathered} {{\psi }_{*}}(x) = {{\psi }_{*}}(0) + \int\limits_0^x {{{v}}_{0}}(s)ds, \\ {{\psi }_{*}}(0) = \int\limits_0^{{{y}_{*}}(0)} {{u}_{{10}}}(\tau )d\tau ,\quad 0 \leqslant x \leqslant X. \\ \end{gathered} $

Введем обозначения

$\begin{gathered} \rho \equiv \rho (x,\psi ) = \left( {\begin{array}{*{20}{c}} {{{\rho }_{1}},}&{0 < \psi \leqslant {{\psi }_{*}}(x),} \\ {{{\rho }_{2}},}&{{{\psi }_{*}}(x) < \psi < \infty ,} \end{array}} \right. \\ \sigma \equiv \sigma (x,\psi ) = \left( {\begin{array}{*{20}{c}} {{{\sigma }_{1}},}&{0 < \psi \leqslant {{\psi }_{*}}(x),} \\ {{{\sigma }_{2}},}&{{{\psi }_{*}}(x) < \psi < \infty .} \end{array}} \right. \\ \end{gathered} $

Далее доказываются теоремы существования и единственности решений полученной задачи (7)–(10) в следующей формулировке.

Теорема 2. Если выполнены предположения теоремы 2, то обобщенное решение $w(x,\psi )$ задачи (7)–(10) существует, причем $w(x,\psi ) \to {{U}^{2}}(x)$ при $\psi \to \infty $ равномерно на отрезке $0 \leqslant x \leqslant X$, а при $0 \leqslant \psi \leqslant {{\psi }_{1}}$ выполняется неравенство

$\left| {{{w}^{{{{\beta }_{1}} - 1}}}\frac{{\partial w}}{{\partial x}}} \right| \leqslant C,\quad 0 < {{\beta }_{1}} < \frac{1}{2},\quad C = {\text{const}}.$

Теорема 3. Если ${{{v}}_{0}}(x) \geqslant 0$ и $\frac{{dp(x)}}{{dx}}$ + + $\sigma B(x)E(x)\, \leqslant \,0$, то решение $w(x,\psi )$, полученное в теореме 2, единственно.

Полученное в теореме 2 обобщенное решение $w(x,\psi )$ при $\psi > {{\psi }_{*}}(x) + \Delta $ имеет обычные производные $\frac{{\partial w}}{{\partial x}}$, $\frac{{\partial w}}{{\partial \psi }}$, $\frac{{{{\partial }^{2}}w}}{{\partial {{\psi }^{2}}}}$, которые ограничены и удовлетворяют условию Гёльдера. Поэтому функция $w(x,\psi )$ является решением уравнения (8) в классическом смысле.

На основе теорем 2 и 3 с помощью обратной замены переменных получаем доказательство основного результата.

Замечание 1. За счет связи градиентов давления и скорости внешнего течения, неравенство $\frac{{dp(x)}}{{dx}} + \sigma B(x)E(x) \leqslant 0$ эквивалентно неравенствам ${{\rho }_{i}}\frac{{dU(x)}}{{dx}} + {{\sigma }_{i}}{{B}^{2}}(x) \geqslant 0$, i = 1, 2, которые выполняются при достаточно большом B2(x). Последнее неравенство означает, что достаточно сильное поперечное магнитное поле предотвращает отрыв пограничного слоя вязкой электропроводной среды. О предотвращении отрыва пограничного слоя см. [12] (а также [14, 15]).

Список литературы

  1. Oleinik O.A. On Stefan–type free boundary problems for parabolic equations. In: Seminary 1962–1963 di analisi, algebra, geometria e topologia, 1. Roma. 1965. P. 388–403.

  2. Oleinik O.A., Primicerio M., Radkevich E.V. Stefan-like problems // Meccanica. 1993. V. 28. P. 129–143.

  3. Ватажин А.Б. О вдувании в пограничный слой в присутствии магнитного поля электропроводной жидкости или газа // Прикл. математика и механика. 1960. Т. 24. № 5. С. 909–911.

  4. Самохин В.Н. Уравнения магнитогидродинамического пограничного слоя с условиями дифракции // Дифф. уравнения. 1997. Т. 33. № 8. С. 1106–1113.

  5. Самохин В.Н. Уравнения магнитогидродинамического пограничного слоя с инъекцией дилатантной среды // Дифф. уравнения. 2010. Т. 46. № 6. С. 846–858.

  6. Самохин В.Н. О системе уравнений стационарного пограничного слоя дилатантной среды // Тр. сем. им. И.Г. Петровского. 1989. Вып. 14. С. 89–108.

  7. Спиридонов С.В., Чечкин Г.А. Просачивание пограничного слоя ньютоновской жидкости через перфорированную преграду // Проблемы математического анализа. 2010. Т. 45. С. 93–102.

  8. Линкевич А.Ю., Спиридонов С.В., Чечкин Г.А. О пограничном слое ньютоновской жидкости, обтекающей шероховатую поверхность и проходящей через перфорированную преграду // Уфимский матем. журн. 2011. Т. 3. № 3. С. 93–104.

  9. Линкевич А.Ю., Спиридонов С.В., Чечкин Г.А. Усреднение стратифицированной дилатантной жидкости // Современная математика. Фундаментальные направления. 2013. Т. 48. С. 75–83.

  10. Chechkin G.A., Chechkina T.P., Ratiu T.S., Romanov M.S. Nematodynamics and Random Homogenization // Applicable Analysis. 2016. V. 95. № 10. P. 2243–2253.

  11. Самохин В.Н., Фадеева Г.М., Чечкин Г.А. Уравнения пограничного слоя для модифицированной системы Навье–Стокса // Тр. сем. им. И.Г. Петровского. 2011. Вып. 28. С. 329–361.

  12. Булатова Р.Р., Самохин В.Н., Чечкин Г.А. Уравнения магнитогидродинамического пограничного слоя для модифицированной несжимаемой вязкой среды. Отрыв пограничного слоя // Проблемы математического анализа. Т. 92. С. 83–100.

  13. Самохин В.Н. О системе уравнений магнитогидродинамического пограничного слоя дилатантной среды // Дифференц. уравнения. 1993. Т. 29. № 2. С. 328–336.

  14. Хуснутдинова Н.В. Об условиях существования безотрывного пограничного слоя при возрастающем давлении // ДАН СССР. 1980. Т. 253. № 5. С. 1095–1099.

  15. Хуснутдинова Н.В. Математические вопросы управления пограничным слоем с помощью отсосов // Сиб. мат. журн. 1972. Т. 13. № 2. С. 485–489.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал