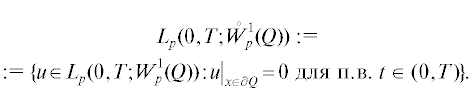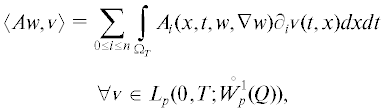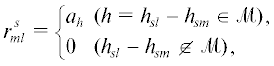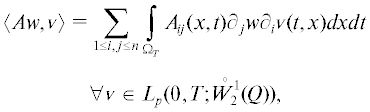Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 503, № 1, стр. 83-86

1. ВВЕДЕНИЕ

Нелокальные краевые задачи рассматриваются с 30-х годов XX века, см. работы Т. Карлемана [1]. В 50-е годы XX-го века началось рассмотрение абстрактных нелокальных задач, см. работы М.И. Вишика [2], Ф. Браудера [3] и др. Среди нелокальных параболических задач на ограниченном множестве наиболее изучены задачи с временными нелокальностями, задачи с интегральными нелокальными членами и задачи на прямоугольнике. В данной работе рассматриваются параболические уравнения с нелокальными краевыми условиями типа Бицадзе–Самарского, ср. [4]. Особенностью данных нелокальных условий является то, что они заданы с помощью сдвигов по пространственным переменным в односвязной ограниченной области. Линейные эллиптические и параболические нелокальные краевые задачи типа Бицадзе–Самарского рассматривались в работах [5–10] и др. Нелинейные эллиптические дифференциальные уравнения с нелокальными краевыми условиями изучались в [11].

2. ПОСТАНОВКА ЗАДАЧИ

Пусть $Q \subset {{\mathbb{R}}^{n}}$ – ограниченная область с границей $\partial Q$ класса C^∞ или $Q = (0,d) \times G$, где $G\, \subset \,{{\mathbb{R}}^{{n - 1}}}$ – ограниченная область (с границей $\partial G$ класса C^∞, если $n \geqslant 3$); $Q = (0,d)$ для n = 1. Определим цилиндр ${{\Omega }_{T}}: = Q \times (0,T)$. Пусть $2 \leqslant p < \infty $, $\frac{1}{p} + \frac{1}{q} = 1$, $f \in {{L}_{q}}(0,T;W_{q}^{{ - 1}}(Q))$, все функции вещественнозначные. В цилиндре ${{\Omega }_{T}}$ рассмотрим дифференциальное уравнение

c нелокальными граничными условиями где множество ${{\Gamma }^{T}} = \{ \Gamma _{{rl}}^{T}\} $ определено следующим образом.

Пусть $\mathcal{M} \subset {{\mathbb{R}}^{n}}$ – конечное множество векторов h с целочисленными (или соизмеримыми) координатами. Через M обозначим аддитивную группу, порожденную множеством $\mathcal{M}$, через Q_r – открытые связные компоненты множества $Q{{\backslash }}\left( {\bigcup\limits_{h \in M} {(\partial Q + h)} } \right)$. Множество Q_r называется подобластью. Семейство $\mathcal{R}$ всех подобластей Q_r ($r = 1,\;2,\; \ldots $) называется разбиением области Q.

Условие 1. Пусть $\mathcal{K}$ = $\bigcup\limits_{{{h}_{1}},{{h}_{2}} \in M} \{ \bar {Q} \cap (\partial Q + {{h}_{1}})$ ∩ ∩ $\overline {[(\partial Q + {{h}_{2}}){{\backslash }}(\partial Q + {{h}_{1}})]} \} $ удовлетворяет условию ${\text{me}}{{{\text{s}}}_{{n - 1}}}(\mathcal{K} \cap \partial Q) = 0$.

Обозначим через ${{\Gamma }_{\rho }}$ открытые, связные в топологии $\partial Q$ компоненты множества $\partial Q{{\backslash }}\mathcal{K}$. Если $({{\Gamma }_{\rho }} + h) \cap \bar {Q} \ne \not {0}$ для некоторого $h \in M$, то или ${{\Gamma }_{\rho }} + h \subset Q$, или существует ${{\Gamma }_{r}} \subset \partial Q{{\backslash }}\mathcal{K}$ такое, что ${{\Gamma }_{\rho }} + h = {{\Gamma }_{r}}$, см. § 7 из [7]. Множества {Γ_ρ + h: ${{\Gamma }_{\rho }} + h \subset \bar {Q},\rho = 1,2, \ldots ,h \in M\} $ могут быть разбиты на классы. ${{\Gamma }_{{{{\rho }_{1}}}}} + {{h}_{1}}$ и ${{\Gamma }_{{{{\rho }_{2}}}}} + {{h}_{2}}$ принадлежат одному классу, если

1) существует вектор $h \in M$ такой, что ${{\Gamma }_{{{{\rho }_{1}}}}}$ + + ${{h}_{1}} = {{\Gamma }_{{{{\rho }_{2}}}}} + {{h}_{2}} + h$;

2) для любых ${{\Gamma }_{{{{\rho }_{1}}}}} + {{h}_{1}},{{\Gamma }_{{{{\rho }_{2}}}}} + {{h}_{2}} \subset \partial Q$ нормали к $\partial Q$ в точках $x \in {{\Gamma }_{{{{\rho }_{1}}}}} + {{h}_{1}}$ и $x - h \in {{\Gamma }_{{{{\rho }_{2}}}}} + {{h}_{2}}$ совпа- дают.

Обозначим множество ${{\Gamma }_{\rho }} + h$ через ${{\Gamma }_{{rj}}}$, где r – номер класса, j – номер элемента в классе ($1 \leqslant j \leqslant J = J(r)$). Не нарушая общности, будем считать, что ${{\Gamma }_{{r1}}},\; \ldots ,\;{{\Gamma }_{{r{{J}_{0}}}}} \subset Q$, ${{\Gamma }_{{r,{{J}_{0}} + 1}}},\; \ldots ,\;{{\Gamma }_{{rJ}}} \subset \partial Q$ ($0 \leqslant {{J}_{0}} = {{J}_{0}}(r) < J = J(r)$). Как известно, см. ${{\S}}$ 7 из [7], для любого ${{\Gamma }_{{rj}}} \subset \partial Q$ существует подобласть ${{Q}_{{sl}}}$ такая, что ${{\Gamma }_{{rj}}} \subset \partial {{Q}_{{sl}}}$. Более того, если ${{\Gamma }_{{rj}}} \subset \partial {{Q}_{{sl}}}$, то ${{\Gamma }_{{rj}}} \cap \partial {{Q}_{{{{s}_{1}}{{l}_{1}}}}} = \not {0}$ для любых $({{s}_{1}},{{l}_{1}}) \ne (s,l)$; и для каждого $r = 1,\;2,\; \ldots $ существует единственный номер $s = s(r)$ такой, что $N(s) = J(r)$ и ${{\Gamma }_{{rl}}} \subset \partial {{Q}_{{sl}}}$ ($l = 1,\; \ldots ,\;N(s)$) (с точностью до перенумеровки). Обозначим теперь $\Gamma _{{rl}}^{T}: = {{\Gamma }_{{rl}}} \times (0,T)$.

Условие 2. Для каждой подобласти ${{Q}_{{sl}}}$ $(s = 1,\;2,\; \ldots $, $l = 1,\; \ldots ,\;N(s))$ и для любого $\varepsilon > 0$ существует  открытое множество ${{G}_{{sl}}} \subset {{Q}_{{sl}}}$ с границей  $\partial {{G}_{{sl}}} \in {{C}^{1}}$  такое,  что  ${\text{me}}{{{\text{s}}}_{n}}({{Q}_{{sl}}}{{\backslash }}{{G}_{{sl}}}) < \varepsilon $, mes_{n – 1} $(\partial {{G}_{{sl}}}\Delta \partial {{Q}_{{sl}}}) < \varepsilon $.

${{L}_{p}}(0,T;W_{p}^{1}(Q))$ – Соболевское пространство функций, интегрируемых на ${{\Omega }_{T}}$ в степени $p$ вместе с первыми производными по x_i, ${\kern 1pt} i = 1,\; \ldots ,\;n$. Обозначим

Периодические по t решения (1), (2) должны удовлетворять условию

Рассматривая производную по t как распределение, введем неограниченный оператор ${{\partial }_{t}}:\mathcal{D}({{\partial }_{t}}) \to {{L}_{q}}(0,T;W_{q}^{{ - 1}}(Q))$ c областью определения

Определим оператор A : L_p(0, T; $W_{{p,\gamma }}^{1}(Q))$ → → L_q(0, T; $W_{q}^{{ - 1}}(Q))$ по формуле

здесь и ниже ${{\partial }_{0}}w: = w$.

Определение 1. Функция w ∈ W_g := := $\mathcal{D}({{\partial }_{t}}) \cap {{L}_{p}}(0,T;W_{{p,\gamma }}^{1}(Q))$ называется обобщенным решением задачи (1)–(3), если она удовлетворяет операторному уравнению

3. РАЗНОСТНЫЙ ОПЕРАТОР И ИЗОМОРФИЗМ ПРОСТРАНСТВ

Рассмотрим набор вещественных постоянных коэффициентов $\{ {{a}_{h}}{\text{:}}\;h \in \mathcal{M}\} $. Определим разностный оператор $R{\text{:}}\;{{L}_{p}}({{\mathbb{R}}^{n}} \times (0,T)) \to {{L}_{p}}({{\mathbb{R}}^{n}} \times (0,T))$:

а также оператор ${{R}_{Q}} = {{P}_{Q}}R{{I}_{Q}}{\text{:}}\;{{L}_{p}}({{\Omega }_{T}}) \to {{L}_{2}}({{\Omega }_{T}})$, здесь ${{I}_{Q}}{\text{:}}\;{{L}_{2}}({{\Omega }_{T}}) \to {{L}_{p}}({{\mathbb{R}}^{n}} \times (0,T))$ – оператор продолжения функций из ${{L}_{2}}({{\Omega }_{T}})$ нулем в $({{\mathbb{R}}^{n}}{{\backslash }}Q)$ × × (0, T), ${{P}_{Q}}{\text{:}}\;{{L}_{p}}({{\mathbb{R}}^{n}} \times (0,T)) \to {{L}_{p}}({{\Omega }_{T}})$ – оператор сужения функций из ${{L}_{p}}({{\mathbb{R}}^{n}} \times (0,T))$ на ${{\Omega }_{T}}$. Для исследования свойств оператора R_Q введем матрицы ${{R}_{s}} = {{\{ r_{{ml}}^{s}\} }_{{1 \leqslant m,l \leqslant N(s)}}}$: где h_sm определяется условием ${{Q}_{{sm}}} = {{Q}_{{s1}}} + {{h}_{{sm}}}$. Из ограниченности области Q и формулы (8) следует, что множество различных матриц ${{R}_{s}}$ конечно.

Пусть ${{\Omega }_{{s1}}}\, = \,{{Q}_{{s1}}}\, \times \,(0,T)$. Изоморфизм U_s : L_p(Ω_s) → → $L_{p}^{N}({{\Omega }_{{s1}}})$ задан по формуле ${{({{U}_{s}}u)}_{l}}(x,t) = u(x + {{h}_{{sl}}}$, t). Оператор ${{R}_{{Qs}}}{\text{:}}\;L_{p}^{N}\left( {{{\Omega }_{{s1}}}} \right) \to L_{p}^{N}\left( {{{\Omega }_{{s1}}}} \right)$, определяемый соотношением ${{R}_{{Qs}}} = {{U}_{s}}{{R}_{Q}}U_{s}^{{ - 1}}$, является оператором умножения на матрицу R_s, при этом R_Q = = $\sum\limits_s U_{s}^{{ - 1}}{{R}_{s}}{{U}_{s}}{{P}_{s}}$, где P_s – проектор на $\bigcup\limits_l {{{Q}_{{sl}}}} \times (0,T)$, см. лемму 8.6 [7] (или лемму 2.6 [8]). Более подробно построение и свойства операторов ${{R}_{Q}}$ и ${{R}_{{Qs}}}$ см. в [7, 8, 10, 11].

Обозначим через ${{R}_{{s(r)}}}$ матрицы, полученные из ${{R}_{s}}{\kern 1pt} (s = s(r))$ путем перенумерования соответствующих столбцов и строк. Пусть $e_{j}^{r}$ ($j = 1,\; \ldots ,\;J(r)$) – $j$-я строка матрицы размерности $J \times {{J}_{0}}$, полученной путем вычеркивания последних $J - {{J}_{0}}$ столбцов из матрицы ${{R}_{{s(r)}}}$.

Определение 2. Будем говорить, что матрицы R_s соответствуют граничным условиям (2), если выполнено следующее

Условие 3. Существует набор $\{ {{a}_{h}} \in \mathbb{R}$ : : $h \in \mathcal{M}\} $ такой, что для любого $s = 1,\;2,\; \ldots $ матрицы R_s невырождены, а также для всех $r \in B$ и $s = s(r)$

Кроме того, обозначим через ${{R}_{{s0}}}$ матрицу порядка ${{J}_{0}} \times {{J}_{0}}$, полученную из матрицы ${{R}_{s}}$ вычеркиванием последних $N(s) - {{J}_{0}}$ строк и столбцов.

Теорема 1. Предположим, что выполнены условия 1–3, а соответствующие матрицы ${{R}_{s}}$ и ${{R}_{{s0}}}$ ($s = s(r)$, $r \in B$) невырождены. Tогда существует множество $\gamma = \{ \gamma _{{ml}}^{r}\} $ такое, что оператор R_Q : 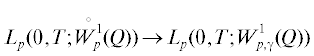 – изоморфизм.

Следствие 1. $w \in {{W}_{\gamma }}$ является обобщенным решением задачи (1)–(3) тогда и только тогда, когда существует решение операторного уравнения

где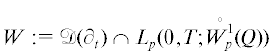 , причем $w = {{R}_{Q}}u$.

4. МАКСИМАЛЬНАЯ МОНОТОННОСТЬ ОПЕРАТОРА ${{\partial }_{t}}{{R}_{Q}}$

Определение 3. Оператор Λ: L_p(0, T; 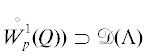$ \to {{L}_{q}}(0,T;W_{q}^{{ - 1}}(Q))$ монотонен, если $\langle \Lambda u - \Lambda {v},u - {v}\rangle \geqslant 0$ для всех $u,{v} \in \mathcal{D}(\Lambda )$. Плотно определенный, монотонный оператор $\Lambda $ максимально монотонен, если не существует нетривиального расширения данного оператора, сохраняющего монотонность.

Как известно, оператор ${{\partial }_{t}}$ с областью определения $\mathcal{D}({{\partial }_{t}}) = W$ максимально монотонен, и $\partial _{t}^{*} = - {{\partial }_{t}}$, см. [12, Гл. 3, п. 2.2].

Лемма 1. ${{\partial }_{t}}{{R}_{Q}}{\text{:}}\;W \to {{L}_{q}}(0,T;W_{q}^{{ - 1}}(Q))$ максимально монотонен.

5. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ ОБОБЩЕННОГО РЕШЕНИЯ

Обозначим через $R_{s}^{{sym}}$ симметрическую часть матрицы ${{R}_{s}}$: $R_{s}^{{sym}} = \frac{1}{2}({{R}_{s}} + R_{s}^{*})$.

Теорема 2. Пусть выполнены условия 1–3; а также $R_{s}^{{sym}} > 0$ ($s = s(r)$, $r \in B$); оператор A: ${{L}_{p}}(0,T;W_{p}^{1}(Q)) \to {{L}_{q}}(0,T;W_{q}^{{ - 1}}(Q))$ задан формулой (5), причем функции ${{A}_{i}}(x,t,\xi )$ измеримы по $(x,t) \in {{\Omega }_{T}}$, T-периодичны по t, дифференцируемы по ${{\xi }_{j}} \in \mathbb{R}$ ($j = 0,\;1,\; \ldots ,\;n$), а также справедливы оценки

где ${{A}_{{ij}}}(x,t,\xi )\,: = \,\frac{{\partial {{A}_{i}}(x,t,\xi )}}{{\partial {{\xi }_{j}}}}$, ${{g}_{0}} \in {{L}_{q}}({{\Omega }_{T}})$, g₁ ∈ ∈ ${{L}_{{p/(p - 2)}}}({{\Omega }_{T}})$, константы ${{c}_{1}},{{c}_{2}},{{c}_{3}} > 0$ не зависят от $(x,t) \in {{\Omega }_{T}}$, $\xi \in {{\mathbb{R}}^{{n + 1}}}$ и $\zeta ,\eta \in {{\mathbb{R}}^{{N(s) \times (n + 1)}}}$, ζ_m· = = $\{ {{\zeta }_{{m0}}},{{\zeta }_{{m1}}},\; \ldots ,\;{{\zeta }_{{mn}}}\} $, $m = 1, \ldots ,N(s)$.

Тогда для любого $f \in {{L}_{q}}(0,T;W_{q}^{{ - 1}}(Q))$ существует единственное обобщенное решение задачи (1)–(3). Более того, если w₁и w₂ – решения, соответствующие правым частям f₁и f₂, то

${{c}_{4}} > 0$ не зависит от ${{w}_{k}} \in {{W}_{\gamma }}$ и ${{f}_{k}}\, \in \,{{L}_{q}}(0,T;W_{q}^{{ - 1}}(Q))$.

При рассмотрении линейного оператора $A$ условия (11)–(13) упростятся.

Теорема 3. Пусть выполнены условия 1–3, а также $R_{s}^{{sym}} > 0$ ($s = s(r)$, $r \in B$); $p = 2$, оператор $A{\text{:}}\;{{L}_{2}}(0,T;W_{2}^{1}(Q)) \to {{L}_{2}}({{\Omega }_{T}})$ задан формулой

причем функции ${{A}_{{ij}}}(x,t)$ измеримы по $(x,t) \in {{\Omega }_{T}}$, M-периодичны по x, T-периодичны по $t$, ${{A}_{{ij}}} \in {{L}_{\infty }}({{\Omega }_{T}})$, а также для некоторого ${{c}_{5}} > 0$, не зависящего от $(x,t) \in {{\Omega }_{T}}$,

Тогда для любого $f \in {{L}_{2}}({{\Omega }_{T}})$ существует единственное решение операторного уравнения (10) $u \in W$. Более того, если ${{w}_{1}} = {{R}_{Q}}{{u}_{1}}$ и ${{w}_{2}} = {{R}_{Q}}{{u}_{2}}$ – решения, соответствующие правым частям f₁и f₂, то

${{c}_{6}} > 0$ не зависит от ${{w}_{k}} \in {{W}_{\gamma }}$ и ${{f}_{k}} \in {{L}_{2}}({{\Omega }_{T}})$.