Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 504, № 1, стр. 42-46
О СХОДИМОСТИ РАЗНОСТНЫХ СХЕМ СКВОЗНОГО СЧЕТА В ОБЛАСТЯХ ВЛИЯНИЯ УДАРНЫХ ВОЛН
О. А. Ковыркина 1, 2, *, В. В. Остапенко 1, 2, **, член-корреспондент РАН В. Ф. Тишкин 3, ***
1 Институт гидродинамики им. М.А. Лаврентьева Сибирского отделения Российской академии наук
Новосибирск, Россия
2 Новосибирский национальный исследовательский государственный университет
Новосибирск, Россия
3 Институт прикладной математики им. М.В. Келдыша Российской академии наук
Москва, Россия
* E-mail: olyana@ngs.ru
** E-mail: ostapenko_vv@ngs.ru
*** E-mail: v.f.tishkin@mail.ru
Поступила в редакцию 04.10.2021
После доработки 24.01.2022
Принята к публикации 28.03.2022
- EDN: AFEFJM
- DOI: 10.31857/S2686954322030043
Аннотация
Проведен сравнительный анализ точности разностных схем Русанова, CABARETM и WENO5 при расчете задачи о разрушении плотины для уравнений теории мелкой воды. Показано, что все три схемы имеют первый порядок сходимости внутри области, занимаемой центрированной волной разрежения, а в области постоянного течения между ударной волной и волной разрежения схема Русанова имеет второй порядок сходимости, в то время как в схемах CABARETM и WENO5 в этой области локальная сходимость отсутствует. Связано это с тем, что численные решения, получаемые по схемам CABARETM и WENO5, имеют незатухающие осцилляции в области влияния ударной волны, амплитуда которых не снижается при уменьшении шагов разностной сетки. В результате, с учетом теоремы Лакса-Вендрофа, численные решения, получаемые по консервативным схемам CABARETM и WENO5, лишь слабо сходятся к точному постоянному решению в области влияния ударной волны, в отличие от схемы Русанова, которая в этой области локально сходится к точному решению со вторым порядком.
1. В работе [1], широко известной в связи со схемой распада разрыва, было введено понятие монотонности разностной схемы и показано, что среди линейных двухслойных по времени схем нет монотонных схем повышенного порядка аппроксимации. Дальнейшее развитие теории разностных схем сквозного счета для гиперболических систем законов сохранения в значительной степени было направлено на преодоление этого “запрета Годунова”. В результате были разработаны различные классы разностных схем, в которых повышенный порядок аппроксимации на гладких решениях и монотонность (при аппроксимации линейной системы и скалярного закона сохранения) достигались за счет нелинейной коррекции потоков, приводящей к нелинейности этих схем даже при аппроксимации линейного уравнения переноса. Перечислим основные классы таких схем, которые будем сокращенно называть NFC (Nonlinear Flux Correction) схемами: MUSCL-схемы [2], WENO-схемы [3], DG-схемы [4] и CABARET-схемы [5]. Основное достоинство этих схем заключается в том, что они с высокой точностью локализуют ударные волны при отсутствии существенных нефизических осцилляций.
Было показано, что NFC-схемы имеют не более чем пеpвый поpядок как локальной сходимости в областях влияния удаpных волн [6, 7], так и интегральной сходимости на интервалах, одна из границ которых находится в области влияния ударной волны [8–10]. В то же время некоторые немонотонные схемы повышенной точности, имеющие аналитические функции численных потоков и, как следствие, с повышенной точностью аппроксимирующие $\varepsilon $-условия Гюгонио, сохраняют повышенный порядок сходимости в негативной норме при интегрировании по областям, содержащим сильные разрывы [8]. В результате эти немонотонные схемы, в отличие от NFC-схем, сохраняют повышенный порядок сходимости в областях влияния ударных волн, несмотря на заметные схемные осцилляции на их фронтах.
В связи с этим был предложен метод построения комбинированных разностных схем сквозного счета [11], которые сочетают достоинства как NFC-схем, так и классических немонотонных схем, а именно, с повышенной точностью локализуют фронты ударных волн и одновременно сохраняют повышенный порядок сходимости в областях их влияния. В комбинированной разностной схеме применяется базисная немонотонная схема, которая имеет повышенный порядок сходимости в областях влияния ударных волн. По базисной схеме разностное решение строится во всей расчетной области. В окрестностях больших градиентов, где это решение имеет нефизические осцилляции, оно корректируется путем численного решения внутренних начально-краевых задач по одной из NFC-схем. В [11] в качестве базисной использовалась схема Русанова [12] третьего порядка классической аппроксимации, а в качестве внутренней NFC-схемы применялась монотонная модификация схемы CABARET [5] второго порядка точности на гладких решениях. Для этой модификации схемы CABARET, изученной в [10], будем использовать аббревиатуру CABARETM.
Один из потенциальных недостатков комбинированной схемы может заключаться в том, что осцилляции, возникающие на фронте ударной волны в немонотонной базисной схеме, с течением времени могут распространяться в гладкие части рассчитываемого точного решения (прежде всего, в область влияния ударной волны), что будет приводить к постепенному расширению расчетной области для внутренней NFC-схемы и к соответствующему снижению эффективности комбинированной схемы. Однако на самом деле имеет место противоположная ситуация. В [13] было обнаружено, что при численном расчете по NFC-схеме DG-метода [4] классической задачи Шу–Ошера [14] за фронтом ударной волны, распространяющейся по энтропийному возмущению, отсутствует локальная сходимость численного решения к точному. Связано это с возникновением численных осцилляций, амплитуда которых перестает убывать при уменьшении пространственного шага сетки, начиная с некоторого его достаточно малого значения.
В настоящей работе показано, что аналогичная проблема возникает при расчете ударных волн и по другим NFC-схемам. А именно, численное решение задачи о разрушении плотины для уравнений мелкой воды, получаемое по немонотонной схеме Русанова [12], несмотря на заметные осцилляции на ударной волне, в области ее влияния монотонно сходится к точному решению со вторым порядком. В то же время численные решения этой задачи, получаемые по NFC-схемам CABARETM [10] и WENO5 [3], имеют незатухающие осцилляции в области постоянного течения между ударной волной и центрированной волной разрежения, что приводит к отсутствию локальной сходимости этих решений в области влияния ударной волны.
2. Векторная форма записи системы законов сохранения первого приближения теории мелкой воды в случае прямоугольного горизонтального русла без учета донного трения имеет вид
где(2)
${\mathbf{u}} = \left( {\begin{array}{*{20}{c}} H \\ q \end{array}} \right),\quad {\mathbf{f}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} q \\ {{{q}^{2}}{\text{/}}H + g{{H}^{2}}{\text{/}}2} \end{array}} \right),$(3)
$H(x,0) = \left\{ \begin{gathered} 5,\quad x \leqslant 0, \hfill \\ 1,\quad x > 0, \hfill \\ \end{gathered} \right.\quad q(x,0) = 0.$Решение этой задачи представляет собой ударную волну, распространяющуюся с постоянной скоростью $D = 6.64$, и центрированную волну понижения, между которыми расположена область постоянного течения. Численное решение задачи (1)–(3) будем строить на равномерной прямоугольной сетке ${{x}_{j}} = jh$, ${{t}_{n}} = n\tau (h)$, в которой временной шаг $\tau (h)$ выбирается из условия устойчивости Куранта
(4)
$\tau (h) = \frac{{zh}}{{\mathop {\max }\limits_{x,t} \max \left( {{\text{|}}{{\lambda }_{ + }}({\mathbf{u}}(x,t)){\text{|}},\;{\text{|}}{{\lambda }_{ - }}({\mathbf{u}}(x,t)){\text{|}}} \right)}},$На рис. 1 и 2 на момент времени T = 1 приведены результаты численных расчетов задачи (1)–(3) по разностным схемам Русанова [12], CABARETM [10] и WENO5 [3]. На рис. 1а показано сравнение точного решения для глубины жидкости с результатами ее численных расчетов на разностной сетке с пространственным шагом h = = 0.36. Из этого рисунка следует, что немонотонная схема Русанова имеет нефизические осцилляции на фронте ударной волны, которые отсутствуют в NFC-схемах CABARETM и WENO5. При этом схема CABARETM размазывает ударную волну и слабые разрывы на границах центрированной волны понижения существенно меньше, чем схема Русанова и схема WENO5.
Рис. 1.
Глубина жидкости (а) и локальные порядки сходимости (б) в момент времени T = 1, получаемые по схемам Русанова (крестики), CABARETM (точки) и WENO5 (кружки); на рисунке (а) сплошная линия – точное решение, пунктирная линия – начальное значение глубины жидкости.
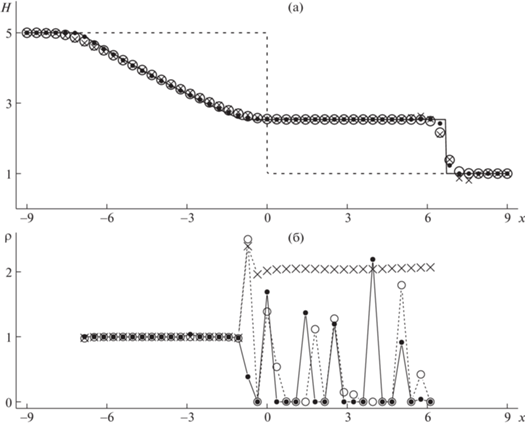
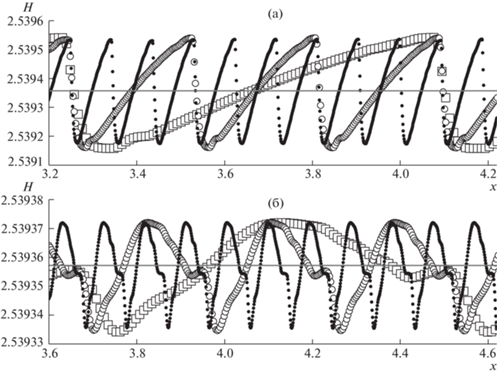
Рис. 2.
Глубина жидкости в области постоянного течения, получаемая при численном расчете по схемам CABARETM (а) и WENO5 (б) на разностных сетках с пространственными шагами $h = 0.009$ (квадратики), $h = 0.003$ (кружки) и $h = 0.001$ (точки); горизонтальная линия – точное решение.
На рис. 1б приведены порядки локальной сходимости разностных решений, которые вычисляются по формуле Рунге
(5)
${{\tilde {\rho }}_{j}} = \mathop {\log }\nolimits_{1/3} \frac{{{\text{|}}{{{\mathbf{v}}}_{{h/3}}}({{x}_{j}}(h),T) - {\mathbf{u}}({{x}_{j}}(h),T){\text{|}}}}{{{\text{|}}{{{\mathbf{v}}}_{h}}({{x}_{j}}(h),T) - {\mathbf{u}}({{x}_{j}}(h),T){\text{|}}}},$(6)
${{\rho }_{j}} = \left\{ \begin{gathered} {{{\tilde {\rho }}}_{j}},\quad 0 \leqslant {{{\tilde {\rho }}}_{j}} \leqslant 2.5, \hfill \\ 0,\quad {{{\tilde {\rho }}}_{j}} < 0, \hfill \\ 2.5,\quad {{{\tilde {\rho }}}_{j}} > 2.5, \hfill \\ \end{gathered} \right.$Для объяснения этих результатов были проведены серии тестовых расчетов на последовательности сжимающихся сеток, которые показали следующее. Разностное решение, получаемое по схеме Русанова, является монотонным (как по глубине, так и по расходу жидкости) внутри области влияния ударной волны вне некоторых окрестностей фронта ударной волны и слабого разрыва на правой границе волны понижения, где со вторым порядком сходится к точному постоянному решению. В то же время разностные решения, получаемые по NFC-схемам CABARETM и WENO5, имеют незатухающие осцилляции в области влияния ударной волны, структура которых зависит от значения параметра z, входящего в условие устойчивости (4). Из рис. 2а видно, что при $z = 0.45$ на отрезке $[3.2,4.2]$, расположенном внутри области влияния ударной волны, схема CABARETM имеет численные осцилляции, амплитуда которых приблизительно одинаковая при пространственных шагах разностной сетки ${{h}_{1}} = h$, ${{h}_{2}} = h{\text{/}}3$ и ${{h}_{3}}$ = = h/9, где $h = 0.009$, а длина волн уменьшается приблизительно в три раза при переходе от сетки с шагом hi к сетке с шагом ${{h}_{{i + 1}}}$, т.е. пропорционально отношению ${{h}_{{i + 1}}}{\text{/}}{{h}_{i}}$. Из рис. 2б подобный результат следует для численных решений схемы WENO5 на отрезке $[3.6,4.6]$. Аналогичное поведение осцилляций в области влияния ударной волны было получено в [13] при расчете DG-методом [4] задачи Шу–Ошера [14]. Из рис. 2 также следует, что амплитуда осцилляций, получаемых при расчете по схеме CABARETM, приблизительно на порядок больше, чем при расчете по схеме WENO5, в то время как длина осцилляционных волн почти одинаковая для обеих схем при фиксированном значении шага сетки hi.
Таким образом, наблюдается следующая общая тенденция: в разностных решениях, получаемых по NFC схемам, может отсутствовать локальная сходимость к точному решению в областях влияния ударных волн. В этом случае, с учетом теоремы Лакса–Вендрофа [15], предельные разрывные решения консервативных NFC схем являются лишь слабыми решениями аппроксимируемой системы законов сохранения в областях влияния ударных волн.
ИСТОЧНИКИ ФИНАНСИРОВАНИЯ
Исследование выполнено при частичной финансовой поддержке РФФИ и ГФЕН (проект № 21-51-53012), а также РНФ (проект № 21-11-00198).
Список литературы
Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики // Мат. сб. 1959. Т. 47. № 3. С. 271–306.
Van Leer B. Toward the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method // J. Comput. Phys. 1979. V. 32. № 1. P. 101–136. https://doi.org/10.1016/0021-9991(79)90145-1
Jiang G.S., Shu C.W. Efficient implementation of weighted ENO schemes // J. Comput. Phys. 1996. V. 126. P. 202–228. https://doi.org/10.1006/jcph.1996.0130
Cockburn B. An introduction to the discontinuous Galerkin method for convection-dominated problems, advanced numerical approximation of nonlinear hyperbolic equations // Lecture Notes in Mathematics. 1998. V. 1697. P. 151–268. https://doi.org/10.1007/BFb0096353
Karabasov S.A., Goloviznin V.M. Compact accurately boundary-adjusting high-resolution technique for fluid dynamics // J. Comput. Phys. 2009. V. 228. P. 7426–7451. https://doi.org/10.1016/j.jcp.2009.06.037
Остапенко В.В. О сходимости разностных схем за фронтом нестационарной ударной волны // Ж. вычисл. матем. и матем. физ. 1997. Т. 37. № 10. С. 1201–1212.
Casper J., Carpenter M.H. Computational consideration for the simulation of shock-induced sound // SIAM J. Sci. Comput. 1998. V. 19. № 1. P. 813–828.
Ковыркина О.А., Остапенко В.В. О сходимости разностных схем сквозного счета // Докл. АН. 2010. Т. 433. № 5. С. 599–603. https://doi.org/10.1134/S1064562410040265
Михайлов Н.А. О порядке сходимости разностных схем WENO за фронтом ударной волны // Матем. моделир. 2015. Т. 27. № 2. С. 129–138. https://doi.org/10.1134/S2070048215050075
Ковыркина О.А., Остапенко В.В. О монотонности и точности схемы КАБАРЕ при расчете обобщенных решений с ударными волнами // Выч. технологии. 2018. Т. 23. № 2. С. 37–54.
Зюзина Н.А., Ковыркина О.А., Остапенко В.В. Монотонная разностная схема, сохраняющая повышенную точность в областях влияния ударных волн // Докл. АН. 2018. Т. 482. № 6. С. 639–643. https://doi.org/10.1134/S1064562418060315
Русанов В.В. Разностные схемы третьего порядка точности для сквозного счета разрывных решений // Докл. АН СССР. 1968. Т. 180. № 6. С. 1303–1305.
Ладонкина М.Е., Неклюдова О.А., Тишкин В.Ф. Решение задач гидродинамики с использованием метода Галеркина с разрывными базисными функциями // Тезисы докладов международной конференции “Современные проблемы прикладной математики и информатики”. С. 20–23 / Дубна, 22–27 августа 2012 г.
Shu C.W., Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes // J. Comput. Phys. 1989. V. 83. № 1 P. 32–78.
Lax P., Wendroff B. Systems of conservation laws // Comm. Pure and Appl. Math. 1960. V. 13. P. 217–237.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


