Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 504, № 1, стр. 83-87

ВВЕДЕНИЕ

Гибкие тканевые защитные экраны активно используются во многих областях техники, в том числе они являются штатной составляющей защитных экранов космических аппаратов, обеспечивающих безопасность пилотируемых станций. Традиционная конструкция защиты на сегодня следует исходным идеям Ф. Уиппла [1] и состоит из трех слоев. Первый слой выполнен из металла и обеспечивает дробление микрометеоритов и космического мусора, превращая сосредоточенный удар крупной высокоскоростной частицы в воздействие облака мелких осколков, распределенное во времени и пространстве. Второй промежуточный слой выполнен из тканевых материалов, он поглощает часть энергии удара и этим дополнительно снижает тепловую и силовую нагрузку. Третьим слоем является непосредственно защищаемая стенка, которая должна уцелеть.

Оптимизация тканевой составляющей защитного экрана является актуальной задачей общего повышения безопасности пилотируемых космических аппаратов. Кроме того, в последнее время дополнительный интерес к тканевым экранам вызван развитием идей использования в составе крупномасштабных космических аппаратов трансформируемых модулей с гибкими стенками. Методы защиты гибких модулей от ударов микрометеоритов и космического мусора являются открытой инженерной задачей [2]. Использование традиционных конструкций защитных экранов с жесткой первой стенкой для гибких модулей малореально, что вызывает активный поиск новых идей [3].

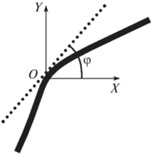
Для быстрых оценок воздействия поперечного удара на тканевые конструкции традиционно используется теория о поперечном ударе по тонкой нити, основанная на работах Рахматулина [4–6] и Смита [7, 8]. В рамках данной теории нить принимается тонкой, в ней действует только сила натяжения, процессы в поперечном сечении нити не рассматриваются. Поперечный удар по такой нити приводит к формированию в ней продольной и поперечной волн. Нить под действием такой нагрузки приобретает типичную V-образную форму, приведенную на рис. 1. Данная форма сохраняется до момента отражения волн от точек закрепления нити или до начала процессов разрушения нити.

Рис. 1.

Форма нити при ударе с постоянной скоростью. Точечный удар (слева) и удар массивным ударником (справа). Пунктирная стрелка показывает направление удара. Сплошными стрелками показаны направления распространения поперечных волн.

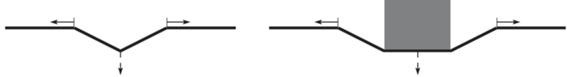
В классической теории получены важные соотношения (1–3), широко используемые в инженерной практике [9], которые связывают скорость продольной волны C_p, скорость поперечной волны C_s, скорость ударника V, деформацию в нити за продольной волной ε.

Данная простая форма записи этих соотношений справедлива только для случаев, в которых нить изначально недеформирована, в ходе всего процесса выполнено условие ${{C}_{s}} \ll {{C}_{p}}$, нить можно принять бесконечно длинной, а скорость ударника постоянной. Однако эти ограничения выполнены для большого количества практически значимых постановок.

Следует отметить, что простые соотношения классической теории не всегда позволяют описать все эффекты, наблюдаемые на практике. Так, некоторые работы сообщают, что отличия экспериментальных данных и оценок по приведенным выше формулам могут достигать 40% [10]. Это вызывает развитие моделей, вводящих учет различных факторов, таких как микроструктура нити и волокон [11, 12]. Также многие наблюдаемые эффекты, оказывается, возможно объяснить, оставаясь в рамках положений классической теории, но решая исходную систему уравнений динамики нити для конкретного случая, а не используя типовые соотношения (1–3). Этому подходу следуют, например, публикации [13, 14]. Данная работа также остается в рамках классической теории Рахматулина, но использует численное решение исходной системы уравнений.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ЧИСЛЕННЫЙ МЕТОД

В данной работе используется исходная система уравнений из [4–6]. Движение нити описывается следующими соотношениями:

Для случая удара с постоянной скоростью система уравнений принимает следующий вид [4]:

В уравнениях (4) и (5) используются следующие обозначения: ${{\rho }_{0}}$ – плотность материала нити, которая принимается постоянной, $T$ – натяжение нити, P – внешняя поперечная нагрузка, приложенная к нити, $\varepsilon $ – деформация нити, ${{s}_{0}}$ – расстояние вдоль нити, $\left( {x;y} \right)$ – пространственные координаты, $\varphi $ – угол между касательной к нити и осью OX. Введенная система координат показана на рис. 2, сплошной линией показан сегмент нити, пунктиром – касательная.

Рис. 2.

Участок нити и используемые обозначения.

Предположение о постоянной скорости удара используется в силу того, что рассматривается массивный ударник, торможением которого за время взаимодействия с одиночной нитью можно пренебречь. Для численного решения приведенной системы используется конечно-разностная схема второго порядка, описание которой приведено в [15].

Отдельно следует рассмотреть вопрос параметрического обеспечения данной модели. Для описания нити требуются ее плотность, модуль Юнга и предел прочности. Плотность не представляет сложностей, в отличие от упругих и прочностных параметров. Для материалов традиционно известны параметры, полученные из статических испытаний. Однако статические значения параметров могут сильно отличаться от динамических, которые материал проявляет при действии ударной нагрузки. Так, по данным работы [16] для Кевлара 49 модуль Юнга и предел прочности меняются более чем на 30% в относительно небольшом диапазоне скоростей деформации.

Для оценки модуля Юнга в интересующем диапазоне скоростей может быть использовано соотношение (1). На начальном этапе удара оно выполняется с хорошей точностью, что позволяет по наблюдаемой в эксперименте скорости поперечной волны и известной скорости ударника получить значение для продольной скорости звука в материале, а из него – динамический модуль Юнга. Следует отметить, что получение значения с высокой точностью таким образом затруднительно, так как модуль Юнга входит в соотношение с малым показателем степени. Тем не менее оценка таким образом может быть получена. Предел прочности может быть найден из решения коэффициентной обратной задачи при наличии достаточного количества экспериментальных данных.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Для валидации использованной модели и метода были взяты экспериментальные данные по материалам публикации [17], которые содержат результаты по воздействию ударной нагрузки на арамидные нити в диапазоне скоростей 200–510 м/с. Среди данных есть постановки как с разрушением нитей, так и с деформированием без обрыва.

Плотность нитей составляет 1440 кг/м³. Динамический модуль Юнга по данным экспериментов может быть оценен как 80 ГПа. Для предельного удлинения при разрушении было взято значение 5%.

Для валидации были использованы эксперименты со скоростями удара 197 и 497 м/с, для которых доступны подробные временные картины формы нити при ее деформировании и разрушении. На рис. 3 и 4 приведены результаты расчетов и их сравнение с экспериментами.

Рис. 3.

Сопоставление расчетов и экспериментов, скорость удара 197 м/с. Между изображениями 10 мкс. По осям пространственные координаты в миллиметрах. Черным показана расчетная форма нити, серым – аппроксимация участка нити, зафиксированного камерой. Край ударника соприкасается с нитью в точке (0; –10), ударник движется влево.

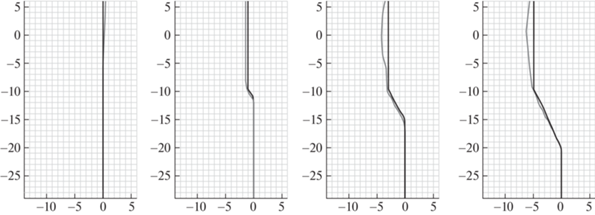
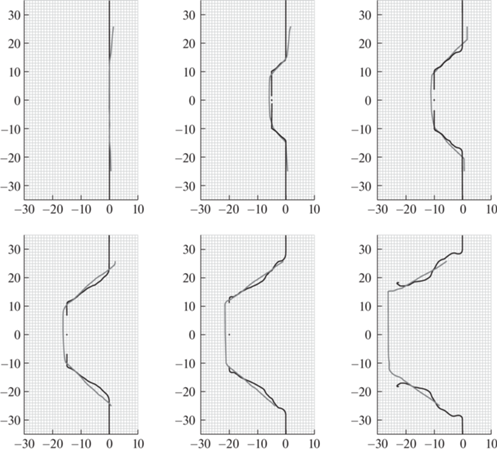
Рис. 4.

Сопоставление расчетов и экспериментов, скорость удара 497 м/с. Между изображениями 10 мкс. По осям пространственные координаты в миллиметрах. Черным показана расчетная форма нити, серым – аппроксимация участка нити, зафиксированного камерой. Край ударника соприкасается с нитью в точке (0; –10), ударник движется влево.

На рис. 3 показаны результаты для удара со скоростью 197 м/с. Исходные экспериментальные данные с покадровым представлением скоростной съемки могут быть найдены в [17]. В данной работе используется поточечно заданная аппроксимация участка нити, зафиксированного камерой. Этот участок на рисунке изображен серой линией. Черным на тех же графиках показана форма нити, полученная в результате расчета в те же моменты времени. В данном режиме разрушения нити не наблюдалось.

Получено хорошее совпадение формы нити, что говорит об адекватности использованных модели и метода. Можно отметить, что в начальный момент времени в эксперименте нить расположена не идеально вертикально, что отличается от постановки расчета. Однако этот факт не сказывается на основном процессе деформирования, в котором экспериментальная и расчетная форма нити совпадают.

Также следует отметить, что в эксперименте наблюдается заметный отскок нити вперед от ударника, который виден как отклонение формы нити от вертикальной в центральной части ударника (около нулевого значения по пространственной оси OY). Этот эффект известен, описан в [10], ожидаем в некоторых режимах деформирования и связан с процессами на толщине нити, которые не входят в модель, использованную в данной работе. Однако наличие данных эффектов не сказывается на движении основной части нити.

На рис. 4 показаны результаты для удара со скоростью 497 м/с, для которого наблюдается разрушение нити. В данном случае серым показан общий контур разрушаемой нити по данным эксперимента, который является огибающей всех ее фрагментов. Это связано с тем, что разрешение скоростной камеры не позволяет точно зафиксировать точку и момент обрыва [17].

Видно, что результаты расчета точно совпадают с данными эксперимента первые 40 мкс процесса, а на завершающей стадии возникает визуально заметное различие в форме фрагментов нити. Это обусловлено математической идеальностью закрепления концов нити в расчете, что приводит к отражению волны разгрузки, образующейся при разрыве нити, от точек закрепления. В эксперименте граничные условия неидеальны, проскальзывание в точке закрепления сглаживает форму нити. При этом общее положение нити и ее фрагментов после разрушения в расчете описаны адекватно.

ЗАКЛЮЧЕНИЕ

В данной работе проведено численное моделирование поперечного удара по арамидным нитям в диапазоне скоростей 200–510 м/с. Выполнено прямое сравнение расчетных и экспериментальных данных как для деформирования без разрушения, так и для постановок с обрывом нитей. Получено хорошее соответствие экспериментов и расчетов по форме деформированной нити (скорости поперечной волны) и по описанию разрыва нити при скорости соударения 500 м/с. Таким образом, математическая модель нити валидирована с использованием экспериментальных результатов в данном скоростном диапазоне.

В дальнейшем данная модель одиночной нити может быть использована при разработке модели гибкого тканевого защитного экрана, состоящего из дискретных нитей. При этом дополнительного исследования потребуют процессы межслойного взаимодействия элементов экрана и ударно-волновые процессы, протекающие на толщине многослойных тканевых пакетов.