Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 504, № 1, стр. 3-27
РАНДОМИЗАЦИЯ И ЭНТРОПИЯ В МАШИННОМ ОБУЧЕНИИ И ОБРАБОТКЕ ДАННЫХ
Академик РАН Ю. С. Попков 1, *
1 Федеральный исследовательский центр “Информатика
и управление” Российской академии наук
Москва, Россия
* E-mail: popkov@isa.ru
Поступила в редакцию 18.02.2022
После доработки 26.02.2022
Принята к публикации 04.03.2022
- EDN: OHYOES
- DOI: 10.31857/S2686954322030079
Аннотация
Сочетание концепции рандомизации с энтропийными критериями позволяет получать решения в условиях максимальной неопределенности, что оказывается весьма эффективным в задачах машинного обучения и обработки данных. Демонстрируется применение этого подхода для энтропийно-рандомизированного оценивания функций на основе данных, рандомизированного “жесткого” и “мягкого” машинного обучения, кластеризации объектов, редукции размерности матрицы данных. Рассматриваются некоторые приложения задачи классификации, прогнозирования электрической нагрузки энергетической системы, рандомизированной кластеризации биологических объектов.
1. ВВЕДЕНИЕ
Обработка данных и машинное обучение являются весьма тесно связанными научными и технологическими направлениями, в рамках которых получено огромное количество результатов, опубликованных в огромном количестве статей и монографий и доложенных на международных конференциях. Ссылки на наиболее цитируемые из них будут сделаны в соответствующих разделах данной работы.
Современная концепция машинного обучения базируется на моделях с обозначенными параметрами, значения которых оцениваются различными методами (в основном математической статистики) с использованием данных с определенными, но гипотетическими, свойствами, и соответствующим образом обработанными и форматированными.
Весьма существенная особенность задач машинного обучения и обработки данных состоит в том, что их решение происходит при наличии недостоверности, неполноты и ошибок в данных, а также при недостаточности знаний об обучаемом объекте, которые проявляются в неадекватности используемых моделей.
Как же преодолеть этот барьер и повысить достоверность, надежность результатов машинного обучения?!
В данной работе предлагается: во-первых, использовать рандомизированные параметризованные модели и оценивать в результате машинного обучения не значения параметров, а их функции плотности распределения вероятности (ПРВ); и во-вторых, использовать не произвольную рандомизацию, а оптимальную, гарантирующую получение наилучших функций ПРВ при максимальной неопределенности. Последнее свойство формулируется в терминах условной максимизации информационной энтропии с учетом имеющихся реальных данных.
Основу предлагаемых методов составляет энтропийно-рандомизированное оценивание функций ПРВ, относительно которого рассматриваются математическая модель, алгоритм и его асимптотическая эффективность. Этот метод оценивания используется в процедурах “жесткого” и “мягкого” рандомизированного машинного обучения и кластеризации объектов.
Одной из проблем обработки данных является редукция их размерности. Предлагается для этой цели использовать энтропийные проекции, которые реализуюся как в детерминированном, так и в рандомизированном алгоритме.
Последний раздел работы посвящен прикладным задачам и иллюстративным примерам. Рассмотрены задачи рандомизированной бинарной классификации с использованием стохастических нейронных сетей, прогнозирования суточной электрической нагрузки энергетической системы, рандомизированной кластеризации биологических объектов.
2. НЕОПРЕДЕЛЕННОСТЬ И РАНДОМИЗАЦИЯ
Подавляющее большинство задач машинного обучения и обработки данных сопровождаются неопределенностью, проявляющейся в ошибках, неполноте, пропусках в массивах данных, в не- адекватности математических моделей исследуемому объекту, в отсутствии надежных знаний о процессах, происходящих в нем, в непредсказуемости окружающей среды.
Декларирование существования неопределенности влечет за собой попытки ее моделирование, хотя бы вербальные, а затем и ее измерение. Со времен Л. Больцмана измерения связывают со статистической энтропией [1, 2] и впоследствии с ее информационной интерпретацией [3]. Известны многочисленные модификации энтропийных функций, связанные с включением в них некоторых особенностей как равновесных состояний макросистем, так и процессов их достижения. Одной из таких модификаций является энтропия Реньи [4], которая обобщает энтропийные функции больцмановского-шеннонского типа [5].
Использование энтропийных функционалов подразумевает некую вероятностную имитацию неопределенного события, т.е. неявно принимается стохастическая модель неопределенности.
Если неопределенное событие интерпретируется как непрерывная переменная, то информационная энтропия определяется через ее функцию плотности распределения вероятностей $P({\mathbf{x}})$:
(2.1)
$\mathcal{H}[P({\mathbf{x}})] = - \int\limits_\mathcal{X} {\kern 1pt} P({\mathbf{x}}){\kern 1pt} \ln P({\mathbf{x}}){\kern 1pt} d{\mathbf{x}},\quad {\mathbf{x}} \in \mathcal{X}.$Если неопределенное событие принадлежит дискретному множеству, то информационная энтропия определяется через вектор p, характеризующий дискретную функцию распределения вероятностей:
(2.2)
$H({\mathbf{p}}) = - \sum\limits_{i = 1}^n {\kern 1pt} {{p}_{i}}{\kern 1pt} \ln {\kern 1pt} {{p}_{i}}.$Поскольку энтропия есть мера неопределенности, то ее максимизация при дополнительных условиях дает наилучшую оценку принятой вероятностной характеристики при максимальной неопределенности [6–8].
Итак, принимается стохастическая концепция неопределенности. Естественным воплощением ее является рандомизированная модель, которая представляет собой генератор ансамбля случайных событий, описываемый функциональной характеристикой, максимизирующей соответствующий энтропийный функционал.
Рандомизация как метод “погружения” исследуемого события (объекта) в ансамбль случайных событий с последующим анализом его числовых характеристик использовался давно и в разных прикладных областях. Прежде всего следует указать на задачи, в которых нужно формировать представительные выборки, например, в клинических исследованиях [9], социальных опросах [10], формировании рейтингов [11] и усредненных сетевых графиков [12] и др.
Рандомизация оказывается полезной в задачах, связанных с предсказанием неких событий с указанием вероятности их наступления. При этом вероятность параметризуется, и данные используются для оценивния указанных параметров [13, 14]. Найденные оценки позволяют вычислить размеры доверительных интервалов. Если эти данные относятся к конкретному индивиду, то найденные таким способом доверительные интервалы квалифицируются как индивидуальные [15].
Идеи рандомизации оказались весьма продуктивными в задачах, где используются нейронные сети. При этом нейронная сеть стала рандомизированной, т.е. содержащей случайные параметры в слоях, в функциях активации, и в количестве слоев [16]. Для обучения такой сети применяется модифицированный алгоритм random forest.
Применение рандомизации при конструировании алгоритмов оказалось весьма эффективным для улучшения их вычислительных свойств. При выполнении некоторых операций запускались соответствующие случайные механизмы, которые при последовательном их выполнении приводили к решению поставленной задачи [17]. Довольно много работ на эту тему в области автоматического управления, где многие задачи управления сводятся к выпуклой и не выпуклой оптимизации. Применение рандомизированных алгоритмов позволяет найти либо точное их решение, либо решение с вероятностью [18–20]. И наконец, следует упомянуть пласт работ по теории игр, где переход к рандомизированным (смешанным) стратегиям позволяет получить решение минимаксной задачи [21].
В данной работе делается очередной шаг в направлении расширения области применения концепции рандомизации. Мы будем синтезировать рандомизированную модель как математическую модель со случайными параметрами. В зависимости от структуры модели случайные параметры характеризуются либо функциями ПРВ, либо функциями РВ, которые определяются с учетом реальных данных и неопределенности путем максимизации энтропийных функционалов. Энтропийно-оптимальные функции ПРВ или РВ сэмплируются, т.е. трансформируются в соответствующие последовательности случайных чисел, и генерируется реальный ансамбль выходов рандомизированной модели. Применяя стандартные методы математической статистики, вычисляются эмпирические числовые характеристики ансамбля: среднее, дисперсию, доверительные интервалы, квантили и др. В результате могут обнаружиться неожиданные свойства рандомизированной модели.
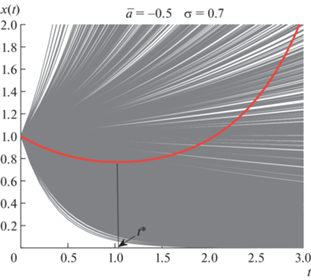
Приведем пример. Рассмотрим модель динамического объекта первого порядка.
Решение этого уравнения
В зависимости от знака a траектория либо убывает, либо возрастает при $t \to \infty $.
Рассмотрим рандомизированную модель, в которой параметр a – случайный с функцией ПРВ
Рандомизированная модель генерирует ансамбль траекторий, средняя траектория в котором имеет вид:
Отсюда следует, что при $\bar {a} \leqslant 0$ траектория имеет минимум в точке $t{\text{*}} = \bar {a}{\text{/}}{{\sigma }^{2}}$, что не реализуется в модели с неслучайным параметром a. Рисунок 1 иллюстрирует описанную ситуацию.
3. ЭНТРОПИЙНО-РАНДОМИЗИРОВАННОЕ ОЦЕНИВАНИЕ (ЭРО) ФУНКЦИЙ ПРВ
3.1. Введение
Существующие методы оценивания функций ПРВ (максимальное правдоподобие, метод моментов, метод наименьших квадратов и др.) никак не учитывают неопределенность, сопровождаемую эти задачи, и требуют задания формы функции и ее параметризацию. Кроме того, приходится принимать весьма обременительные и непроверяемые гипотезы о свойствах данных как выборки из генеральной совокупности [22, 23].
3.2. Математическая формулировка метода ЭРО
Рассмотрим скалярную аналитическую функцию $\hat {y} = \varphi (x,\theta )$ с рандомизированными параметрами $\theta = \{ {{\theta }_{1}}, \ldots ,{{\theta }_{n}}\} $ интервального типа, т.е.
Вероятностные свойства параметров характеризуются функцией плотности распределения вероятностей (ПРВ) $P(\theta )$, определенной на множестве $\mathcal{E}$.
Поскольку параметры рандомизированные, то и переменная $\hat {y}$ – рандомизирована и принимает значения в множестве $\hat {\mathcal{Y}}$, размеры которого определяются функцией $\varphi (x,\theta )$ и вероятностными свойствами параметров.
Пусть имеются r измерений $\{ {{x}_{1}}, \ldots ,{{x}_{r}}\} = {{{\mathbf{x}}}^{{(r)}}}$, и $\{ {{y}_{1}}, \ldots ,{{y}_{r}}\} = {{{\mathbf{y}}}^{{(r)}}}$. В результате имеем следующую систему уравнений:
где вектор-функция ${\mathbf{\Phi }}({{{\mathbf{x}}}^{{(r)}}},{\mathbf{\theta }})$ имеет компоненты $\varphi ({{x}_{t}},{\mathbf{\theta }}),t = \overline {1,r} $.Вектор ${\mathbf{\hat {y}}}$ (3.2) – рандомизированный. Рассмотрим в качестве его числовых характеристик r-мерный вектор с компонентами в виде нормированных моментов $s$-й степени:
(3.3)
${{{\mathbf{m}}}^{{(s)}}}[P(\theta )] = {{\left( {\int\limits_\mathcal{E} {\kern 1pt} P(\theta ){{\Phi }^{s}}({{{\mathbf{x}}}^{{(r)}}},\theta ){\kern 1pt} d{\kern 1pt} \theta } \right)}^{{\frac{1}{s}}}}.$Заметим, что (3.3) является векторным функционалом от функции ПРВ $P(\theta )$.
Измеренные данные в виде вектора ${{{\mathbf{y}}}^{{(r)}}}$, будем приравнивать векторам нормированных моментов11:
Из этих выражений следует, что совпадение моментных характеристик ансамбля рандомизированных переменных зависит от функции ПРВ $P(\theta )$.
Таким образом, задача оценивания функции ПРВ параметров формулируется следующим образом [25]:
(3.5)
$\mathcal{H}[P(\theta )] = - \int\limits_\mathcal{E} P(\theta )\ln P(\theta )d\theta \Rightarrow \mathop {\max }\limits_{P(\theta )} $– нормировки функций ПРВ
– эмпирических балансов
Задача (3.5)–(3.7) относится к классу ляпуновских [26, 27], которые характеризуются тем, что функционалы и ограничения интегрального типа и выпуклые.
3.3. Условия оптимальности
Условия оптимальности в задачах оптимизации ляпуновского типа формулируются в терминах вещественных множителей Лагранжа. При этом используются производные Гато интегральных функционалов [29].
Для задачи (3.5)–(3.7) функционал Лагранжа имеет вид:
(3.8)
$\begin{gathered} \mathcal{L}[P(\theta ),\lambda ] = \mathcal{H}[P(\theta )] + \mu \left( {1 - \int\limits_\mathcal{E} P(\theta )d\theta } \right) + \\ \, + \langle \lambda ,({{{\mathbf{y}}}^{{(r)}}} - {{{\mathbf{m}}}^{{(s)}}}[P(\theta )])\rangle . \\ \end{gathered} $Технике получения условий оптимальности в терминах производной Гато посвящено Приложение A.
Используя условия оптимальности (1.1), получим оптимальную функцию ПРВ, параметризованную множителями Лагранжа $\theta $:
(3.9)
$\begin{gathered} P{\kern 1pt} *(\theta \,{\text{|}}\,{\kern 1pt} \lambda ) = \frac{{\exp (\langle \lambda ,{{\Phi }^{s}}({{{\mathbf{x}}}^{{(r)}}},\theta )\rangle )}}{{\mathcal{P}(\lambda )}}, \\ \mathcal{P}(\lambda ) = \int\limits_\mathcal{E} \exp (\langle \lambda ,{{\Phi }^{s}}({{{\mathbf{x}}}^{{(r)}}},\theta )\rangle )d\theta . \\ \end{gathered} $Из равенств (3.9) видно, что энтропийно-оптимальная функция ПРВ параметризована множителями Лагранжа λ, которые определяются решением уравнений эмпирических балансов:
(3.10)
${{\mathcal{P}}^{{ - 1}}}(\lambda )\int\limits_\mathcal{E} \,{{\Phi }^{s}}({{{\mathbf{x}}}^{{(r)}}},\theta )\exp (\langle \lambda ,{{\Phi }^{s}}({{{\mathbf{x}}}^{{(r)}}},\theta )\rangle ) = {{{\mathbf{y}}}^{{(r)}}}.$Решение этих уравнений – неявная функция $\lambda = \lambda {\kern 1pt} *({{{\mathbf{y}}}^{{(r)}}}),{{{\mathbf{x}}}^{{(r)}}})$ зависит от измеренных данных $({{{\mathbf{y}}}^{{(r)}}}$, x(r)), по которым строятся ЭРО функции ПРВ.
Важным частным случаем ЭРО является балансирование с данными средних характеристик ансамбля (3.3):
(3.11)
${{{\mathbf{m}}}^{{(1)}}}[P(\theta )] = \int\limits_\mathcal{E} {\kern 1pt} P(\theta )\Phi ({{{\mathbf{x}}}^{{(r)}}},\theta ){\kern 1pt} d{\kern 1pt} \theta .$В этом случае в формулах (3.8)–(3.10) s = 1.
3.4. Существование неявной функции $\lambda ({{{\mathbf{y}}}^{{(r)}}},{{{\mathbf{x}}}^{{(r)}}})$
Рассмотрим балансовые уравнения для средних числовых характеристик ансамбля (3.3):
(3.12)
$\begin{gathered} \int\limits_\mathcal{E} {\kern 1pt} (\Phi ({{{\mathbf{x}}}^{{(r)}}},\theta ) - {{{\mathbf{y}}}^{{(r)}}}){\kern 1pt} \exp (\langle \lambda ,\Phi ({{{\mathbf{x}}}^{{(r)}}},\theta )\rangle ){\kern 1pt} d\theta = \\ \, = {\mathbf{W}}(\lambda \,{\text{|}}\,{{{\mathbf{x}}}^{r}},{{{\mathbf{y}}}^{r}}) = {\mathbf{0}}, \\ \end{gathered} $Якобиан функции W имеет вид:
(3.13)
${{J}_{\lambda }}(\lambda \,{\text{|}}\,{{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{{(r)}}}) = \left[ {\frac{{\partial {{W}_{t}}}}{{\partial {{\lambda }_{i}}}},\,{\text{|}}\,(t,i) = \overline {1,r} } \right],$(3.14)
$\begin{gathered} \frac{{\partial {{W}_{t}}}}{{\partial {{\lambda }_{i}}}} = \int\limits_\mathcal{E} \left( {\varphi ({{x}_{t}},\theta ) - {{y}_{t}}} \right)\varphi ({{x}_{i}},\theta ) \times \\ \, \times \sum\limits_{j = 1}^r \exp \left( { - \sum\limits_{j = 1}^r {{\lambda }_{j}}\varphi ({{x}_{j}},\theta )} \right)d\theta . \\ \end{gathered} $Теорема 1. Пусть:
• a) функция $\Phi ({{{\mathbf{x}}}^{{(r)}}},\theta )$ непрерывна по совокупности переменных;
• b) для любых $({{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{{(r)}}}) \in {{R}^{r}} \times {{R}^{r}}$ выполняются следующие условия
(3.15)
$\det {{J}_{\lambda }}(\lambda \,{\text{|}}\,{{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{{(r)}}}) \ne 0,$(3.16)
$\mathop {\lim }\limits_{\parallel \lambda \parallel \to \infty } {\mathbf{W}}({\mathbf{\lambda }}\,{\text{|}}\,{{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{{(r)}}}) = \pm \infty .$Тогда существует единственная неявная функция $\lambda ({{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{{(r)}}})$, определенная на ${{R}^{r}} \times {{R}^{r}}$.
Доказательство этой теоремы приведено в Приложении $B$.
Теорема 2. Пусть выполнены условия теоремы 1. Тогда функция $\lambda ({{{\mathbf{y}}}^{{(r)}}},{{{\mathbf{x}}}^{{(r)}}})$ – аналитическая по совокупности перменных.
Доказательство теоремы 2 приведено в Приложении B.
3.5. Асимптотика ЭРО
ЭРО дает энтропийно оптимальную ПРВ (3.10), (3.11) для наборов данных ${{{\mathbf{x}}}^{{(r)}}},\;{{{\mathbf{y}}}^{{(r)}}}$ объемами r каждый.
Далее удобнее оперировать функциями ПРВ, параметризованными экспоненциальными множителями Лагранжа ${\mathbf{z}} = \exp ( - \lambda )$. Тогда равенство (3.10) примет следующий вид:
(3.17)
$\begin{gathered} P{\text{*}}(\theta ,{\mathbf{z}}) = \frac{{\prod\limits_{j = 1}^r {{{[{{z}_{j}}]}}^{{\varphi ({{x}_{j}},\theta )}}}}}{{\mathcal{P}({\mathbf{z}})}}, \\ \mathcal{P}({\mathbf{z}}) = \int\limits_\mathcal{E} \,\prod\limits_{j = 1}^r {{[{{z}_{j}}]}^{{\varphi ({{x}_{j}},\theta )}}}{\kern 1pt} d\theta . \\ \end{gathered} $Отсюда видно, что структура функции ПРВ зависит от значений экспоненциальных множителей Лагранжа z, которые, в свою очередь, зависят от от коллекции данных ${{{\mathbf{x}}}^{{(r)}}},\;{{{\mathbf{y}}}^{{(r)}}}$.
Определение. Будем называть оценку функции ПРВ $P{\kern 1pt} {\text{*}}(\theta ,{\mathbf{z}}{\kern 1pt} *)$ асимптотически устойчивой, если
(3.18)
$\mathop {\lim }\limits_{r \to \infty } P{\kern 1pt} {\text{*}}(\theta ,{\mathbf{z}}({{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{{(r)}}})) = P{\kern 1pt} {\text{*}}(\theta ,{\mathbf{\tilde {z}}}),$(3.19)
${\mathbf{\tilde {z}}} = \mathop {\lim }\limits_{r \to \infty } {\mathbf{z}}({{{\mathbf{y}}}^{{(r)}}},{{{\mathbf{x}}}^{{(r)}}}).$Рассмотрим уравнения эмпирических балансов (3.12), перейдя в них к экспоненциальным множителям Лагранжа:
(3.20)
$\begin{gathered} {{\Theta }_{t}}({\mathbf{z}},{{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{r}})) = \\ \, = \int\limits_\mathcal{E} \,\prod\limits_{j = 1}^r {{[{{z}_{j}}({{{\mathbf{x}}}^{{(r)}}},{{{\mathbf{y}}}^{r}})]}^{{\varphi ({{x}_{j}},\theta )}}}\left( {\varphi ({{x}_{t}},\theta ) - {{y}_{t}}} \right)d\theta = 0, \\ t = \overline {1,r} . \\ \end{gathered} $В предыдущем разделе было показано, что уравнения (3.12) определяют неявную аналитическую функцию $\theta ({{{\mathbf{x}}}^{r}}),{{{\mathbf{y}}}^{{(r)}}})$.
В силу связи множителей и экспоненциальных множителей Лагранжа уравнения (3.20) определяют неявную аналитическую функцию z = ${\mathbf{z}}({{{\mathbf{x}}}^{r}})$, y(r)) для $({{{\mathbf{x}}}^{r}},{{{\mathbf{y}}}^{{(r)}}}) \in {{R}^{r}} \times {{R}^{r}}$.
Дифференцируем левую и правую часть этих уравнений по ${{{\mathbf{x}}}^{{(r)}}}$ и ${{{\mathbf{y}}}^{{(r)}}}$. Получим следующие уравнения:
(3.21)
$\frac{{\partial {\mathbf{z}}}}{{\partial {{{\mathbf{x}}}^{{(r)}}}}} = - {{\left[ {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right]}^{{ - 1}}}\frac{{\partial \Theta }}{{\partial {{{\mathbf{x}}}^{{(r)}}}}},\quad \frac{{\partial {\mathbf{z}}}}{{\partial {{{\mathbf{y}}}^{{(r)}}}}} = - {{\left[ {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right]}^{{ - 1}}}\frac{{\partial \Theta }}{{\partial {{{\mathbf{y}}}^{{(r)}}}}}.$Все матрицы в этих уравнениях квадратные, размера (r × r).
Переходя к нормам, получим следующие неравенства:
(3.22)
$\begin{gathered} 0 \leqslant \left\| {\frac{{\partial {\mathbf{z}}}}{{\partial {{{\mathbf{x}}}^{{(r)}}}}}} \right\| \leqslant \left\| {{{{\left[ {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right]}}^{{ - 1}}}} \right\|\left\| {\frac{{\partial \Theta }}{{\partial {{{\mathbf{x}}}^{{(r)}}}}}} \right\|, \\ 0 \leqslant \left\| {\frac{{\partial {\mathbf{z}}}}{{\partial {{{\mathbf{y}}}^{{(r)}}}}}} \right\| \leqslant \left\| {{{{\left[ {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right]}}^{{ - 1}}}} \right\|\left\| {\frac{{\partial \Theta }}{{\partial {{{\mathbf{y}}}^{{(r)}}}}}} \right\|. \\ \end{gathered} $В оба эти неравенства входит норма обратной матрицы $\left\| {{{{\left[ {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right]}}^{{ - 1}}}} \right\|$.
Лемма 1. Пусть квадратная матрица A – невырождена, т.е. $\det A \ne 0$. Тогда существует константа α > 1, такая, что
(3.23)
$\frac{1}{{\left\| A \right\|}} \leqslant \left\| {{{A}^{{ - 1}}}} \right\| \leqslant \frac{\alpha }{{\left\| A \right\|}}.$Доказательство леммы 1 приведено в Приложении C.
Применим неравенство (3.23) к норме обратной матрицы $\left\| {{{{\left[ {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right]}}^{{ - 1}}}} \right\|$. Получим следующее неравенство:
(3.24)
${{\left( {\left\| {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right\|} \right)}^{{ - 1}}} \leqslant \left\| {{{{\left[ {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right]}}^{{ - 1}}}} \right\| \leqslant \alpha {{\left( {\left\| {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right\|} \right)}^{{ - 1}}}.$В этих неравенствах (см. [28])
(3.25)
$\left\| {\frac{{\partial \Theta }}{{\partial {\mathbf{z}}}}} \right\| = r\mathop {\max }\limits_{t,j} \left| {\frac{{\partial {{\theta }_{t}}}}{{\partial {{z}_{j}}}}} \right| = r\theta .$Лемма 2. Пусть
(3.26)
$\left\| {\frac{{\partial \Theta }}{{\partial {{{\mathbf{x}}}^{{(r)}}}}}} \right\| \leqslant \rho < \infty ,\quad \left\| {\frac{{\partial \Theta }}{{\partial {{{\mathbf{y}}}^{{(r)}}}}}} \right\| \leqslant \omega < \infty .$Тогда оценка функции ПРВ $P{\text{*}}({\mathbf{\theta }},{\mathbf{z}}{\text{*}})$ асимптотически устойчива в смысле (3.18), (3.19)
Доказательство леммы 2 приведено в Приложении D.
4. РАНДОМИЗИРОВАННОЕ МАШИННОЕ ОБУЧЕНИЕ (РМО)
4.1. Введение
Машинное обучение является одним из трендовых направлений современной науки и технологий. Количество публикаций, посвященных машинному обучению, превышает десятки тысяч и продолжает расти. Основное их количество связано с разнообразными приложениями, особенности которых порождают и новые задачи исследовательского характера [32, 34–36]. Несмотря на разнообразие работ по машинному обучению, их фундаментальная основа строится на методах математической статистики, а точнее, на методах оценивания вещественных параметров моделей.
Рандомизированное машинное обучение использует принципиально иной подход, связанный с оцениванием функций плотности распределения вероятностей с неизвестной структурой и параметрами. Развиваются методы оценивания функций ПРВ, основанные на условной (с учетом имеющихся данных) максимизации энтропии [37].
4.2. Постановка задачи
Рассмотрим РМО-процедуру применительно к задаче восстановления зависимостей. Предполагается, что имеются данные о входе ${{{\mathbf{x}}}^{{(r)}}}[k] \in {{R}^{n}}$ и выходе ${{{\mathbf{y}}}^{{(r)}}}[k] \in {{R}^{m}}$ объекта на временном интервале $\mathcal{T} = [0,T]$, где $k = \overline {0,T} $. На интервале наблюдения формируются блочные векторы входных и выходных данных:
(4.1)
$\begin{gathered} {{{\mathbf{X}}}^{{(r)}}} = \{ {{{\mathbf{x}}}^{{(r)}}}[0], \ldots ,{{{\mathbf{x}}}^{{(r)}}}[T]\} , \\ {{{\mathbf{Y}}}^{{(r)}}} = \{ {{{\mathbf{y}}}^{{(r)}}}[0], \ldots ,{{{\mathbf{y}}}^{{(r)}}}[T]\} , \\ \end{gathered} $Они сопровождаются случайными и независимыми измерительными шумами (ошибками) с заданными областями их значений (интервалами):
(4.2)
$\begin{gathered} \eta [k] \in {{\mathcal{E}}_{k}} = [\eta {{[k]}^{ - }},{{\eta }^{ + }}[k]], \\ \xi [k] \in {{\mathcal{K}}_{k}} = [\xi {{[k]}^{ - }},{{\xi }^{ + }}[k]],\quad k = \overline {0,T} . \\ \end{gathered} $Измерительные шумы на интервале $\mathcal{T}$ будем так же характеризовать соответствующими блочными векторами:
(4.3)
$\begin{gathered} \eta \to {\mathbf{E}} = \{ \eta [0], \ldots ,\eta [T{{]\} }^{ \intercal }} - n(T + 1) - {\text{вектор}}, \\ \xi \to {\mathbf{K}} = \{ \xi [0], \ldots ,\xi [T{{]\} }^{ \intercal }} - m(T + 1) - {\text{вектор}}. \\ \end{gathered} $Согласно (4.2) области значений этих векторов имеют вид:
(4.4)
${\mathbf{E}} \in \mathcal{E} = \bigcup\limits_{k = 0}^T {{\mathcal{E}}_{k}},\quad {\mathbf{K}} \in \mathcal{K} = \bigcup\limits_{k = 0}^T {{\mathcal{K}}_{k}}.$Наблюдаемые входные ${\mathbf{\hat {x}}}[k]$ и выходные данные v[k] предположительно аддитивно связаны с измерительными шумами:
(4.5)
$\begin{gathered} {\mathbf{\hat {x}}}[k] = {{{\mathbf{x}}}^{{(r)}}}[k] + \eta [k],\quad {\mathbf{v}}[k] = {\mathbf{\hat {y}}}[k] + \xi [k], \\ k = \overline {0,T} , \\ \end{gathered} $(4.6)
${\mathbf{\hat {y}}}[k] = {\mathbf{f}}({{{\mathbf{x}}}^{{(r)}}}[k] + \eta [k]\,{\text{|}}\,{\mathbf{a}}),$На интервале наблюдения $\mathcal{T}$ будем иметь:
(4.8)
$\begin{gathered} {\mathbf{V}} = {\mathbf{\hat {Y}}} + \mathcal{K}, \\ {\mathbf{\hat {Y}}} = {\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}), \\ \end{gathered} $(4.9)
$\begin{gathered} {\mathbf{\hat {Y}}} = \{ {\mathbf{\hat {y}}}[0], \ldots ,{\mathbf{\hat {y}}}[T{{]\} }^{ \top }} - \\ \, - n(T + 1) - {\text{блочный вектор}}, \\ {\mathbf{F}} = \{ {\mathbf{f}}({{{\mathbf{x}}}^{{(r)}}}[0] + \eta 0]),...,{\mathbf{f}}({{{\mathbf{x}}}^{{(r)}}}[T] + \eta [T{{])\} }^{ \top }}. \\ \end{gathered} $Поскольку параметры и измерительные ошибки являются случайными объектами, введем для их характеризации
• совместную функцию ПРВ $W({\mathbf{a}},{\mathbf{E}})$, определенную на множестве
(4.10)
$\mathcal{W} = \mathcal{A} \cup \mathcal{E},\quad ({\mathbf{a}},{\mathbf{E}}) \in \mathcal{W},$• функцию ПРВ Q(K), определенную на множестве $\mathcal{K}$ (4.4).
Таким образом, используя наборы реальных данных ${{{\mathbf{X}}}^{{(r)}}}$ и ${{{\mathbf{Y}}}^{{(r)}}}$, определить функции ПРВ $W({\mathbf{a}}$, E) и Q(K).
4.3. Алгоритм “жесткого” РМО для восстановления функций ПРВ параметров и шумов
Алгоритм РМО для случая 1-моментных эмпирических балансов (“жесткое” РМО) имеет вид:
(4.11)
$\begin{gathered} \mathcal{H}\left[ {W({\mathbf{a}},{\mathbf{E}}),Q({\mathbf{K}})} \right] = \\ = - \int\limits_\mathcal{W} {\kern 1pt} W({\mathbf{a}},{\mathbf{E}}){\kern 1pt} \ln W({\mathbf{a}},{\mathbf{E}}){\kern 1pt} d{\mathbf{a}}{\kern 1pt} d{\kern 1pt} {\mathbf{E}} - \\ \, - \int\limits_\mathcal{K} {\kern 1pt} Q({\mathbf{K}}){\kern 1pt} \ln Q({\mathbf{K}}){\kern 1pt} d{\kern 1pt} {\mathbf{K}} \Rightarrow \max , \\ \end{gathered} $– нормировки функций ПРВ
(4.12)
$\int\limits_\mathcal{W} {\kern 1pt} W({\mathbf{a}},{\mathbf{E}}){\kern 1pt} d{\mathbf{a}}{\kern 1pt} d{\kern 1pt} {\mathbf{E}} = 1,\quad \int\limits_\mathcal{K} \,Q({\mathbf{K}}){\kern 1pt} d{\kern 1pt} {\mathbf{K}} = 1;$– эмпирических балансов 1-й степени
(4.13)
$\begin{gathered} \int\limits_\mathcal{W} {\kern 1pt} W({\mathbf{a}},{\mathbf{E}}){\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}}) \otimes d{\mathbf{a}} \otimes d{\mathbf{E}} + \\ \, + \int\limits_\mathcal{K} \,Q({\mathbf{K}}){\mathbf{K}} \otimes d{\mathbf{K}} = {{{\mathbf{Y}}}^{{(r)}}}, \\ \end{gathered} $Применяя технику формирования условий оптимальности с помощью производных Гато (см. Приложение B), получим следующие выражения для энтропийно-оптимальных функций ПРВ параметров и измерительных шумов, параметризованных множителями Лагранжа $\Lambda $ и зависящих от входных ${{{\mathbf{X}}}^{{(r)}}}$ и выходных ${{{\mathbf{Y}}}^{{(r)}}}$ данных:
(4.14)
$\begin{gathered} W{\kern 1pt} {\text{*}}({\mathbf{a}},{\mathbf{E}}\,{\text{|}}\,\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) = \\ \, = {{{\mathbf{W}}}^{{ - 1}}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) \otimes \overline {\exp } (\langle \Lambda ,{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}})\rangle ), \\ Q{\kern 1pt} {\text{*}}({\mathbf{K}}\,{\text{|}}\,\Lambda ) = {{{\mathbf{Q}}}^{{ - 1}}}(\Lambda ) \otimes \overline {\exp } \left( {\langle \Lambda ,{\mathbf{K}}\rangle } \right), \\ \end{gathered} $(4.15)
$\begin{gathered} {\mathbf{W}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}})\, = \,\int\limits_\mathcal{W} \,\overline {\exp } (\langle \Lambda ,{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}}\, + \,{\mathbf{E}}\,{\text{|}}\,{\mathbf{a}})\rangle )\, \otimes \,d{\mathbf{a}} \otimes d{\mathbf{E}}, \\ {\mathbf{Q}}(\Lambda ) = \int\limits_\mathcal{K} \,\overline {\exp } \left( {\langle \Lambda ,{\mathbf{K}}\rangle } \right) \otimes d{\mathbf{K}}. \\ \end{gathered} $В этих равенствах $\overline {\exp } $ – вектор с компонентами $\exp ( \bullet )$.
Множители Лагранжа $\Lambda $ определяются следующими уравнениями:
(4.16)
$\begin{gathered} {\mathbf{R}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) \otimes {\mathbf{Q}}(\Lambda ) + {\mathbf{G}}(\Lambda ) \otimes {\mathbf{W}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) = \\ \, = {{{\mathbf{Y}}}^{{(r)}}} \otimes {\mathbf{Q}}(\Lambda ) \otimes {\mathbf{W}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}), \\ \end{gathered} $(4.17)
$\begin{gathered} {\mathbf{R}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) = \int\limits_\mathcal{W} \,{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}}) \otimes \\ \, \otimes \overline {\exp } (\langle \Lambda ,{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}})\rangle ) \otimes d{\mathbf{a}} \otimes d{\mathbf{E}}, \\ {\mathbf{G}}(\Lambda ) = \int\limits_\mathcal{K} \,{\mathbf{K}} \otimes \overline {\exp } \left( {\langle \Lambda ,{\mathbf{K}}\rangle } \right) \otimes d{\mathbf{K}}. \\ \end{gathered} $Из приведенных выражений следует, что оценки функций ПРВ параметров и измерительных шумов, соответствующие максимальной (в единицах информационной энтропии) неопределенности, зависят не только от имеющихся данных о входе и выходе исследуемого объекта, но и от модели объекта. Причем в общем случае нелинейной модели вероятностные свойства рандомизированных параметров и измерительных шумов на входе характеризуются оптимальной оценкой совместной функции ПРВ. Последнее свидетельствует о связи вероятностных свойств энтропийно-рандомизированных параметров и входных измерительных шумов.
Если предполагается, что входные данные измеряются точно, т.е. $\eta = 0$, процедура формирования оценок функций ПРВ упрощается. В этом случае имеем:
(4.18)
${\mathbf{\hat {y}}}[k] = {\mathbf{f}}({{{\mathbf{x}}}^{{(r)}}}[k]{\kern 1pt} |{\kern 1pt} {\mathbf{a}}).$В принятых выше обозначениях функции ПРВ параметров и шумов приобретают следующий вид:
(4.19)
$\begin{gathered} W{\kern 1pt} {\text{*}}({\mathbf{a}}\,{\text{|}}\,\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) = {{{\mathbf{W}}}^{{ - 1}}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) \otimes \overline {\exp } \left( {\langle \Lambda ,{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}}\,{\text{|}}\,{\mathbf{a}})\rangle } \right), \\ Q{\kern 1pt} {\text{*}}({\mathbf{K}}\,{\text{|}}\,\Lambda ) = {{{\mathbf{Q}}}^{{ - 1}}}(\Lambda ) \otimes \overline {\exp } \left( {\langle \Lambda ,{\mathbf{K}}\rangle } \right), \\ \end{gathered} $(4.20)
$\begin{gathered} {\mathbf{W}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) = \int\limits_\mathcal{W} \,\overline {\exp } (\langle \Lambda ,{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}}\,{\text{|}}\,{\mathbf{a}})\rangle ) \otimes d{\mathbf{a}}, \\ {\mathbf{Q}}(\Lambda ) = \int\limits_\mathcal{K} \,\overline {\exp } \left( {\langle \Lambda ,{\mathbf{K}}\rangle } \right) \otimes d{\kern 1pt} {\mathbf{K}}. \\ \end{gathered} $Множители Лагранжа определяются из уравнения (4.16), где
(4.21)
$\begin{gathered} {\mathbf{R}}(\Lambda ,{{{\mathbf{X}}}^{{(r)}}}) = \\ = \int\limits_\mathcal{W} {\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}}\,{\text{|}}\,{\mathbf{a}})\, \otimes \,\overline {\exp } (\langle \Lambda ,{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}}\,{\text{|}}\,{\mathbf{a}})\rangle ) \otimes d{\mathbf{a}}, \\ {\mathbf{G}}(\Lambda ) = \int\limits_\mathcal{K} \,{\mathbf{K}} \otimes \overline {\exp } \left( {\langle \Lambda ,{\mathbf{K}}\rangle } \right) \otimes d{\mathbf{K}}. \\ \end{gathered} $4.4. Алгоритм “мягкого” РМО для восстановления функций ПРВ
В некоторых задачах РМО не требуется строгое выполнение балансов между числовыми характеристиками ансамбля выхода модели и данными. Учитывая (4.5), (4.6), воспользуемся евклидовым расстоянием между наблюдаемым выходом модели и данными в виде:
(4.22)
$\begin{gathered} \, = {\text{||}}{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}}) + {\mathbf{K}} - {{{\mathbf{Y}}}^{{(r)}}}{\text{|}}{{{\text{|}}}_{E}} \leqslant \\ \, \leqslant {\text{||}}{\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}}){\text{|}}{{{\text{|}}}_{E}} + \,{\text{||}}{\mathbf{K}} - {{{\mathbf{Y}}}^{{(r)}}}{\text{|}}{{{\text{|}}}_{E}} = \\ \end{gathered} $Из этих равенств следует, что верхняя граница расстояния $\bar {\varrho }$ является функцией случайных параметров a и измерительных шумов E, K.
Определим функционал $\mathcal{R}$, являющийся средним функции $\bar {\varrho }$:
(4.23)
$\begin{gathered} \mathcal{R}[W({\mathbf{a}},{\mathbf{E}}),Q({\mathbf{K}})] = \\ \, = \int\limits_{\mathcal{W} \times \mathcal{E}} W({\mathbf{a}},{\mathbf{E}}){\kern 1pt} {{\varrho }_{1}}({\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,|\,{\mathbf{a}}) \otimes d{\mathbf{a}} \otimes d{\mathbf{E}} + \\ \, + \int\limits_\mathcal{K} \,Q({\mathbf{K}}){{\varrho }_{2}}({\mathbf{K}} - {{{\mathbf{Y}}}^{{(r)}}}) \otimes d{\mathbf{K}}. \\ \end{gathered} $Алгоритм “мягкого” РМО имеет вид:
(4.24)
$\begin{gathered} \mathcal{J}[W({\mathbf{a}},{\mathbf{E}}),Q({\mathbf{K}})] = - \mathcal{H}[W({\mathbf{a}},{\mathbf{E}}),Q({\mathbf{K}})] - \\ \, - \mathcal{R}[W({\mathbf{a}},{\mathbf{E}}),Q({\mathbf{K}})] \Rightarrow \max , \\ \end{gathered} $(4.25)
$\int\limits_{\mathcal{W} \times \mathcal{E}} {\kern 1pt} W({\mathbf{a}},{\mathbf{E}}){\kern 1pt} d{\mathbf{a}} \otimes d{\kern 1pt} {\mathbf{E}} = 1,\quad \int\limits_\mathcal{K} \,Q({\mathbf{K}}){\kern 1pt} d{\kern 1pt} {\mathbf{K}} = 1.$Задача оптимизации (4.24), (4.25) также ляпуновского типа, и ее решение имеет вид:
(4.26)
$\begin{gathered} W{\kern 1pt} {\text{*}}({\mathbf{a}},{\mathbf{E}}) = {{\mathbb{W}}^{{ - 1}}}{\kern 1pt} \exp ({{\varrho }_{1}}({\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}})), \\ Q{\kern 1pt} {\text{*}}({\mathbf{K}}) = {{\mathbb{Q}}^{{ - 1}}}{\kern 1pt} \exp ({{\varrho }_{2}}({\mathbf{K}} - {{{\mathbf{Y}}}^{{(r)}}})), \\ \end{gathered} $(4.27)
$\begin{gathered} \mathbb{W} = \int\limits_{\mathcal{W} \times \mathcal{E}} {\kern 1pt} \exp ({{\varrho }_{1}}({\mathbf{F}}({{{\mathbf{X}}}^{{(r)}}} + {\mathbf{E}}\,{\text{|}}\,{\mathbf{a}})) \otimes d{\mathbf{a}} \otimes d{\mathbf{E}}, \\ \mathbb{Q} = \int\limits_\mathcal{K} {\kern 1pt} \exp ({{\varrho }_{2}}({\mathbf{K}} - {{{\mathbf{Y}}}^{{(r)}}})) \otimes d{\mathbf{K}}. \\ \end{gathered} $Алгоритм “мягкого” РМО позволяет получать аналитические выражения для энтропийно-оптимальных ПРВ параметров и шумов, не требующие решения балансовых уравнений. Из (4.26) следует, что эти ПРВ экспоненциального класса, но их морфология определяется не только структурой математической модели, но и принятыми векторными нормами.
5. КЛАСТЕРИЗАЦИЯ ОБЪЕКТОВ НА ОСНОВЕ ЭРО
Метод энтропийно-рандомизированного оценивания, изложенный в первом разделе, позволяет восстанавливать функции ПРВ случайных параметров. До сих пор рассматривались непрерывно-дифференцируемые функции ПРВ. Однако существует класс задач, где присутствуют дискретные рандомизированные объекты. Ансамбли таких объектов характеризуются дискретными функциями распределения вероятностей, значения которых принадлежат интервалу [0, 1], или дискретными функциональными формами распределения вероятностей, значения которых принадлежат неотрицательному интервалу $[0,\infty )$. Одними из таковых являются задачи кластеризации.
5.1. Введение
Кластеризация объектов различной природы является одним из направлений машинного обучения, в котором метки учителя заменяются какими-то внутренними характеристиками объектов или внешними характеристиками кластеров. К внутренним относятся расстояния между объектами внутри кластера [50, 51], характристики сходства объектов [52], а к внешним – расстояния между кластерами [53]. Как математическая задача, кластеризация не имеет универсальной формулировки, и поэтому алгоритмы кластеризиции носят, как правило, эвристический характер [54, 55].
Весьма развитое направление связано с кластеризацией больших массивов текстов. Ему обычно предшествуют процедуры выявления скрытых признаков, основанные на латентном семантическом анализе [56], которые затем используются для кластеризации [57, 58].
Большинство алгоритмов кластеризации используют расстояние между объектами, измеряемое в принятой метрике, и переборные алгоритмы с эвристическим управлением [59]. Результаты кластеризации существенно зависят от принятой метрики. Поэтому числовая оценка качества кластеризации оказывается весьма важной [60–62].
Предлагаемый метод кластеризации основан на рандомизированном представлении ансамбля возможных кластеров, характеризуемым функцией распределения вероятностей.
5.2. Принцип рандомизированной кластеризации
Рассмотрим n объектов, состояние каждого характеризуется вектором ${{{\mathbf{x}}}^{{(i)}}} \in {{R}^{m}}$. В указанном пространстве множество объектов отображается в облако из $n$ точек. Пусть, для начала, это множество точек нужно разделить на два подмножества – кластера ${{\mathcal{K}}_{s}}$ и ${{\mathcal{K}}_{{n - s}}}$ с заданными объемами (количеством объектов) s и $n - s$.
Поскольку количество объектов конечно и объем кластера ${{\mathcal{K}}_{s}}$ задан, то формально можно образовать конечное количество кластеров типа ${{\mathcal{K}}_{s}}$ объемом s, но с различным составом объектов. Отбор объектов в кластеры будем производить случайным образом и независимо друг от друга. Количество таких кластеров равно числу сочетаний $C_{n}^{s} = \frac{{n!}}{{s!(n - s)!}}$, но состав их образован случайным механизмом. Из оставшихся объектов образуются кластеры типа ${{\mathcal{K}}_{{n - s}}}$.
Таким образом, сформирован ансамбль рандомизированных кластеров ${{\mathcal{K}}_{s}}$, объема $C_{n}^{s}$, который характеризуется пока неизвестной дискретной функцией распределения вероятностей p(k, s), где $k \to \{ {{i}_{1}}, \ldots ,{{i}_{s}}\} $ – номер конкретного кластера в ансамбле; ${{i}_{1}}, \ldots ,{{i}_{s}}$ – номера объектов, входящих в k‑кластер.
Для определения функции p(k, s) воспользуемся методом энтропийно-рандомизированного оценивания (ЕРО). Согласно этому методу свойства оптимальности функции p(k, s) характеризуются максимумом информационной энтропии при условии, что принятый средний показатель качества ансамбля кластеров принимает заданное значение.
Тогда наиболее вероятный кластер в ансамбле определяется максимумом функции p*(k*, s) = = ${\text{ma}}{{{\text{x}}}_{k}}p{\text{*}}(k,s)$. Поскольку информационная энтропия определяется функцией распределения вероятностей, то вычисляется ее значение $H{\kern 1pt} {\text{*}}(s)$ для $p{\kern 1pt} {\text{*}}(k,s)$, и определяется $s{\kern 1pt} {\text{*}} = {{\max }_{s}}H{\kern 1pt} {\text{*}}(s)$.
5.3. Числовая характеристика множества объектов
Рассмотрим множество из $n$ объектов, каждый из которых характеризуеся вектором ${{{\mathbf{x}}}^{{(i)}}}(i = \overline {1,n} )$ из пространства ${{R}^{m}}$. Математическим образом совокупности объектов является блочный вектор следующего вида:
(5.1)
${{{\mathbf{X}}}^{{(1, \ldots ,n)}}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{x}}}^{{(1)}}}} \\ \cdots \\ {{{{\mathbf{x}}}^{{(n)}}}} \end{array}} \right)$Определим расстояние между его компонентами – векторами ${{{\mathbf{x}}}^{{(i)}}}(i = \overline {1,n} )$ в виде:
(5.2)
$\varrho ({{{\mathbf{x}}}^{{(i)}}},{{{\mathbf{x}}}^{{(j)}}}) = {\text{||}}{{{\mathbf{x}}}^{{(i)}}} - {{{\mathbf{x}}}^{{(j)}}}{\text{|}}{{{\text{|}}}_{{{{R}^{m}}}}},$(5.3)
${{D}_{{(n \times n)}}} = \left( {\begin{array}{*{20}{c}} 0&{\varrho ({{{\mathbf{x}}}^{{(1)}}},{{{\mathbf{x}}}^{{(2)}}})}& \cdots &{\varrho ({{{\mathbf{x}}}^{{(1)}}},{{{\mathbf{x}}}^{{(n)}}})} \\ {\varrho ({{{\mathbf{x}}}^{{(2)}}},{{{\mathbf{x}}}^{{(1)}}})}&0& \cdots &{\varrho ({{{\mathbf{x}}}^{{(2)}}},{{{\mathbf{x}}}^{{(n)}}})} \\ \cdots & \cdots & \cdots &{} \\ {\varrho ({{{\mathbf{x}}}^{{(n)}}},{{{\mathbf{x}}}^{{(1)}}})}&{\varrho ({{{\mathbf{x}}}^{{(n)}}},{{{\mathbf{x}}}^{{(2)}}})}& \cdots &0 \end{array}} \right).$Определим в качестве числовой характеристики вектора ${{{\mathbf{X}}}^{{(1, \ldots ,n)}}}$ среднее значение элементов матрицы расстояний ${{D}_{{(n \times n)}}}$, которое будем обозначать ${\text{dis}}{\kern 1pt} ({{{\mathbf{X}}}^{{(1, \ldots ,n)}}})$ и называть индикатором вектора ${{{\mathbf{X}}}^{{(1, \ldots ,n)}}}$:
(5.4)
${\text{dis}}{\kern 1pt} ({{{\mathbf{X}}}^{{(1, \ldots ,n)}}}) = \frac{1}{{{{n}^{2}}}}\sum\limits_{(i,j) = 1}^n {\kern 1pt} \varrho ({{{\mathbf{x}}}^{{(i)}}},{{{\mathbf{x}}}^{{(j)}}}).$Важной характеристикой вектора ${{{\mathbf{X}}}^{{(1, \ldots ,n)}}}$ являются минимальный и максимальный элементы матрицы расстояний ${{D}_{{(n \times n)}}}$:
(5.5)
$\begin{gathered} {\text{inf}}{\kern 1pt} ({{D}_{{(n \times n)}}}) = \mathop {\min }\limits_{i,j} {\kern 1pt} \varrho ({{{\mathbf{x}}}^{{(i)}}},{{{\mathbf{x}}}^{{(j)}}}), \\ {\text{sup}}{\kern 1pt} ({{D}_{{(n \times n)}}}) = \mathop {\max }\limits_{i,j} \varrho ({{{\mathbf{x}}}^{{(i)}}},{{{\mathbf{x}}}^{{(j)}}}). \\ \end{gathered} $Заметим, что элементы матриц расстояний формируемых кластеров должны принадлежать интервалу
5.4. Алгоритм рандомизированной бинарной кластеризации
Задача бинарной кластеризации состоит в распределении n объектов по двум кластерам ${{\mathcal{K}}_{{(s{\kern 1pt} *)}}}$, ${{\mathcal{K}}_{{(n - s{\kern 1pt} *)}}}$ с объемами s* и $(n - s{\kern 1pt} *)$ объектов соответственно:
(5.7)
$\begin{gathered} {{\mathcal{K}}_{{(s{\kern 1pt} *)}}} = \{ {{i}_{1}}, \ldots ,{{i}_{{s{\kern 1pt} *}}}\} ,\quad {{\mathcal{K}}_{{(n - s{\kern 1pt} *)}}} = \{ {{j}_{1}}, \ldots ,{{j}_{{(n - s{\kern 1pt} *)}}}\} ; \\ ({{i}_{1}}, \ldots ,{{i}_{s}}) \ne ({{j}_{1}}, \ldots ,{{j}_{{(n - s{\kern 1pt} *)}}}),\quad ({{i}_{\alpha }},{{j}_{\beta }}) = \overline {1,n} , \\ \alpha = \overline {1,s{\kern 1pt} *} ,\quad \beta = \overline {1,n - s{\kern 1pt} *} . \\ \end{gathered} $1. $s = \tilde {s}$ – задано. При каждом фиксированном объеме кластера, т.е. значении $\tilde {s}$, процедура его формирования состоит в выделении в векторе ${{{\mathbf{X}}}^{{(1, \ldots ,n)}}}$ подвектора
(5.8)
${{{\mathbf{x}}}_{{(\tilde {s})}}} = {\mathbf{x}}_{{(\tilde {s})}}^{{({{i}_{1}}, \ldots ,{{i}_{{\tilde {s}}}})}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{x}}}^{{({{i}_{1}})}}}} \\ \cdots \\ {{{{\mathbf{x}}}^{{({{i}_{{\tilde {s}}}})}}}} \end{array}} \right),$Если подвектор ${\mathbf{X}}_{{(\tilde {s})}}^{{({{i}_{1}}, \ldots ,{{i}_{{\tilde {s}}}})}}$ выделен, то оставшиеся компоненты образуют подвектор ${{{\mathbf{X}}}_{{(n - \tilde {s})}}} = {\mathbf{X}}_{{(n - \tilde {s})}}^{{{{j}_{1}}, \ldots ,{{j}_{{n - \tilde {s}}}}}}$, а совокупность номеров оставшихся компонент образуют кластер ${{\mathcal{K}}_{{(n - \tilde {s})}}}$.
Согласно принципу рандомизированной бинарной кластеризации вектор ${{{\mathbf{x}}}_{{(\tilde {s})}}}$ объявляется случайным. Перенумеруем набор
(5.9)
$\{ {{i}_{1}}, \ldots ,{{i}_{{\tilde {s}}}}\} \to k = \overline {1,K(\tilde {s})} ;\quad K(\tilde {s}) = C_{{\tilde {s}}}^{n}.$Таким образом, в результате рандомизации генерируется конечный ансамбль случайных векторов:
(5.10)
${{\mathcal{X}}_{{(\tilde {s})}}} = \{ {\mathbf{X}}_{{(\tilde {s})}}^{1}, \ldots ,{\mathbf{X}}_{{(\tilde {s})}}^{{K(\tilde {s})}}\} .$Поскольку векторы в этом ансамбле случайные, то существуют вероятности реализации элементов этого ансамбля, т.е. функция распределения вероятностей $p(\tilde {s},k)$, где $\tilde {s}$ – объем кластера, а k – номер его реализации:
(5.11)
${\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}\;{\text{с вероятностью}}\;p(\tilde {s},k),\quad k = \overline {1,K(\tilde {s})} .$Итак, задача рандомизированной бинарной кластеризации сводится к определению подходящей в каком-то смысле функции дискретного распределения вероятностей $p(\tilde {s},k),{\kern 1pt} {\kern 1pt} k = \overline {1,K(\tilde {s})} )$.
Рассмотрим кластер ${{\mathcal{K}}_{1}}$ объемом $\tilde {s}$ и соответствующий ему блочный вектор:
(5.12)
${\mathbf{X}}_{{(\tilde {s})}}^{{({{i}_{1}}, \ldots ,{{i}_{{\tilde {s}}}})}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{x}}}^{{({{i}_{1}})}}}} \\ \cdots \\ {{{{\mathbf{x}}}^{{({{i}_{{\tilde {s}}}})}}}} \end{array}} \right) = {\mathbf{X}}_{{(\tilde {s})}}^{{(k)}},\quad \{ {{i}_{1}}, \ldots ,{{i}_{{\tilde {s}}}}\} \to k,$(5.13)
$\begin{gathered} D_{{(\tilde {s})}}^{{({{i}_{1}}, \ldots ,{{i}_{{\tilde {s}}}})}} = \\ = \,\left( {\begin{array}{*{20}{c}} 0&{{{\varrho }^{{(k)}}}({{{\mathbf{x}}}^{{{{i}_{1}}}}},{\kern 1pt} {{{\mathbf{x}}}^{{{{i}_{2}}}}})}& \cdots &{{{\varrho }^{{(k)}}}({{{\mathbf{x}}}^{{{{i}_{1}}}}},{\kern 1pt} {{{\mathbf{x}}}^{{{{i}_{{\tilde {s}}}}}}})} \\ \cdots & \cdots & \cdots &{} \\ {{{\varrho }^{{(k)}}}({{{\mathbf{x}}}^{{{{i}_{{\tilde {s}}}}}}},{\kern 1pt} {{{\mathbf{x}}}^{{{{i}_{1}}}}})}&{{{\varrho }^{{(k)}}}({{{\mathbf{x}}}^{{{{i}_{{\tilde {s}}}}]}}},{\kern 1pt} {{{\mathbf{x}}}^{{{{i}_{2}}}}})}& \cdots &0 \end{array}} \right)\, = \,D_{{(\tilde {s})}}^{{(k)}}. \\ \end{gathered} $Воспользуемся понятием индикатора матрицы (5.4) и определим его для кластера ${{\mathcal{K}}_{s}}$ в виде:
(5.14)
${\text{dis}}{\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}) = \frac{1}{{{{{\tilde {s}}}^{2}}}}\sum\limits_{(t,h) = 1}^{\tilde {s}} {\kern 1pt} {{\varrho }^{{(k)}}}({{{\mathbf{x}}}^{{{{i}_{t}}}}},{{{\mathbf{x}}}^{{{{i}_{h}}}}}).$Поскольку векторы ${\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}$ предполагаются случайными объектами, на их ансамбле существует функция распределения $p(\tilde {s},k)$. Определим средний индикатор в виде:
(5.15)
$\mathcal{M}\{ {\text{dis}}{\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}})\} = \sum\limits_{k = 1}^{K(\tilde {s})} {\kern 1pt} p(\tilde {s},k){\kern 1pt} {\text{dis}}{\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}).$Сформулируем алгоритм бинарной кластеризации при фиксированном значении $s = \tilde {s}$ в следующем виде:
– максимизация энтропийного функционала Больцмана-Шеннона:
(5.16)
${{\mathcal{H}}_{B}}[p(\tilde {s},k){\kern 1pt} |{\kern 1pt} \tilde {s}] = - \sum\limits_{k = 1}^{K(\tilde {s})} p(\tilde {s},k){\text{ln}}p(\tilde {s},k) \Rightarrow \mathop {\max }\limits_{p(\tilde {s},k)} ,$– при ограничениях:
(5.18)
${\text{inf}}(D) \leqslant \sum\limits_{k = 1}^{K(\tilde {s})} {\kern 1pt} p(\tilde {s},k){\kern 1pt} {\text{dis}}{\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}) \leqslant {\text{sup}}(D),$Задача (5.16)–(5.18) является конечно-мерной. Ограничения (5.17) можно опустить, если в качестве целевого функционала использовать энтропию Ферми [49]. После преобразований будем иметь следующую конечно-мерную задачу энтропийно-линейного программирования [64]:
(5.19)
$\sum\limits_{k = 1}^{K(\tilde {s})} {\kern 1pt} p(\tilde {s},k){\kern 1pt} \overline {{\text{dis}}} {\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}})\, \leqslant \, - {\kern 1pt} 1,\quad \overline {{\text{dis}}} {\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}})\, = \, - {\kern 1pt} \frac{{{\text{dis}}{\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}})}}{{\inf (D)}}$Функция Лагранжа имеет вид:
(5.20)
$\begin{gathered} L[{\mathbf{p}},{{\lambda }_{1}},{{\lambda }_{2}}{\kern 1pt} |{\kern 1pt} \tilde {s}] = H({\mathbf{p}}{\kern 1pt} |{\kern 1pt} \tilde {s}) + \\ \, + {{\lambda }_{1}}{\kern 1pt} \left( { - 1 - \sum\limits_{k = 1}^{K(\tilde {s}} {\kern 1pt} p(\tilde {s},k){\kern 1pt} \overline {{\text{dis}}} {\kern 1pt} (X_{{(\tilde {s})}}^{{(k)}})} \right) + \\ \, + {{\lambda }_{2}}{\kern 1pt} \left( {1 - \sum\limits_{k = 1}^{K(\tilde {s})} {\kern 1pt} p(\tilde {s},k){\kern 1pt} \underline {{\text{dis}}} {\kern 1pt} (X_{{(\tilde {s})}}^{{(k)}})} \right). \\ \end{gathered} $Согласно теоремы Куна–Таккера [65], условия оптимальности имеют вид:
Первая группа условий аналитически разрешима относительно компонент вектора ${\mathbf{p}}$:
(5.21)
$\begin{gathered} p{\kern 1pt} {\text{*}}(\tilde {s},k\,{\text{|}}\,{{\lambda }_{1}},{{\lambda }_{2}}) = \\ \, = \frac{{\exp ( - {{\lambda }_{1}}{\kern 1pt} \overline {{\text{dis}}} {\kern 1pt} (X_{{(\tilde {s})}}^{{(k)}}) - {{\lambda }_{2}}{\kern 1pt} \underline {{\text{dis}}} {\kern 1pt} (X_{{(\tilde {s})}}^{{(k)}}))}}{{1 + \exp ( - {{\lambda }_{1}}{\kern 1pt} \overline {{\text{dis}}} {\kern 1pt} (X_{{(\tilde {s})}}^{{(k)}}) - {{\lambda }_{2}}{\kern 1pt} \underline {{\text{dis}}} {\kern 1pt} (X_{{(\tilde {s})}}^{{(k)}}))}}, \\ k = \overline {1,K(\tilde {s})} . \\ \end{gathered} $Вторая группа условий преобразуется в следующие неравенства:
(5.22)
$\begin{gathered} \, = - 1 - \sum\limits_{k = 1}^{K(\tilde {s})} {\kern 1pt} p{\kern 1pt} {\text{*}}(\tilde {s},k\,{\text{|}}\,\lambda _{1}^{*},\lambda _{2}^{*}){\kern 1pt} \overline {{\text{dis}}} {\kern 1pt} (X_{{(\tilde {s})}}^{{(k)}}) \geqslant 0, \\ {{L}_{{{{\lambda }_{2}}}}}(p{\kern 1pt} {\text{*}}(\tilde {s},k\,{\text{|}}\,\lambda _{1}^{*},\lambda _{2}^{*}) = \\ \end{gathered} $Третья группа условий сводится к следующим уравнениям:
(5.23)
$\lambda _{2}^{*}{\kern 1pt} {{L}_{{{{\lambda }_{2}}}}}(p{\kern 1pt} {\text{*}}(\tilde {s},k\,{\text{|}}\,\lambda _{1}^{*},\lambda _{2}^{*}) = 0,$Для определения неотрицательного решения указанных уравнений можно применить мультипликативный алгоритм следующего вида [49]:
(5.24)
$\begin{gathered} \lambda _{1}^{{q + 1}} = \lambda _{1}^{q}{\kern 1pt} (1 + \gamma {{L}_{{{{\lambda }_{1}}}}}(p{\kern 1pt} {\text{*}}(\tilde {s},k\,{\text{|}}\,\lambda _{1}^{q},\lambda _{2}^{q})), \\ \lambda _{2}^{{q + 1}} = \lambda _{2}^{q}{\kern 1pt} (1 + \gamma {{L}_{{{{\lambda }_{2}}}}}(p{\kern 1pt} {\text{*}}(\tilde {s},k\,{\text{|}}\,\lambda _{1}^{q},\lambda _{2}^{q})), \\ (\lambda _{1}^{0},\lambda _{2}^{0}) > 0. \\ \end{gathered} $Здесь $\gamma > 0$ – параметр, выбираемый из условий $\mathfrak{G}$-сходимости итерационного процесса (5.24).
Алгоритм (5.24) называется $\mathfrak{G}$-сходящимся, если в пространстве $R_{ + }^{2}$ существует множество $\mathfrak{G}$ и скаляры $a(\mathfrak{G})$ и γ такие, что для всех $(\lambda _{1}^{0},\lambda _{2}^{0}) \in \mathfrak{G}$ и $0 < \gamma \leqslant a(\mathfrak{G})$ он сходится к решению $\lambda _{1}^{*},\;\lambda _{2}^{*}$ уравнения (5.23), причем сходимость в окрестности $\lambda _{1}^{*},\;\lambda _{2}^{*}$ – линейная.
Теорема 3. Алгоритм (5.24) $\mathfrak{G}$-сходится к решению задачи (5.24).
Доказательство приведено в Приложении Е.
Таким образом, определена функция распределения вероятностей
(5.25)
$\begin{gathered} p{\kern 1pt} {\text{*}}(\tilde {s},k\,{\text{|}}\,\lambda _{1}^{*},\lambda _{2}^{*}) = \\ \, = \frac{{\exp ( - \lambda _{1}^{*}{\kern 1pt} \overline {{\text{dis}}} {\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}) - \lambda _{2}^{*}{\kern 1pt} \underline {{\text{dis}}} {\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}))}}{{1 + \exp ( - \lambda _{1}^{*}{\kern 1pt} \overline {{\text{dis}}} {\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}) - \lambda _{2}^{*}{\kern 1pt} \underline {{\text{dis}}} {\kern 1pt} ({\mathbf{X}}_{{(\tilde {s})}}^{{(k)}}))}}, \\ k = \overline {1,K(s)} . \\ \end{gathered} $Естественно предположить, что, согласно общему принципу статистической механики, реализуемый кластер (при фиксированном объеме $\tilde {s}$) соответствует максимуму функции распределения вероятностей, т.е.
(5.26)
${{\mathcal{K}}_{{\tilde {s},k{\kern 1pt} *}}} \Rightarrow (\tilde {s},k{\kern 1pt} *) = \mathop {\max }\limits_k p{\text{*}}(\tilde {s},k\,{\text{|}}\,\lambda _{1}^{*},\lambda _{2}^{*}).$2. $s = \overline {1,n - 1} $. Рассмотрим случай, когда объем кластера не задан, т.е $\tilde {s} = s$, которое принимает значения в интервале $[1,n - 1]$. При этом образуется последовательность максимальных значений информационной энтропии
(5.27)
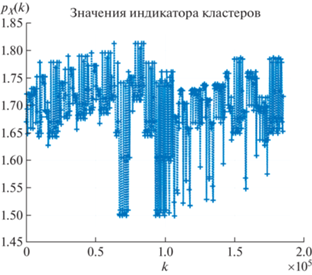
${{H}_{B}}(s) = - \sum\limits_{k = 1}^{K(s)} p{\kern 1pt} {\text{*}}(s,k{\kern 1pt} *){\text{ln}}p{\kern 1pt} {\text{*}}(s,k{\kern 1pt} *).$Оптимальное значение объема кластера определяется максимальным элементом в этой последовательности:
6. ЭНТРОПИЙНЫЕ ПРОЕКЦИИ ДЛЯ РЕДУКЦИИ РАЗМЕРНОСТИ МАТРИЦЫ ДАННЫХ
Во многих прикладных задачах обработки данных последние форматируются в виде прямоугольных матриц ${{U}_{{(m \times s)}}}$. Без ограничения общности будем считать m – количество объектов (прецендентов), s – количество признаков.
По разным причинам возникает необходимость “сжать” матрицу данных, т.е. трансформировать ее в матрицу, размерности $(m \times r)$ или $(n \times r)$, $n < m$, $r < s$.
Данная проблема вложена в более общую: приближение заданного набора многомерных точек маломерным аффинным многообразием [38]. Здесь следует отметить метод главных компонент (МГК) [39] и его робастные версии [40], а так же метод случайных проекций [41, 42].
В [43] был предложен энтропийный метод одномерного (столбцы или строки) детерминированного сжатия матрицы данных (EDR-метод), основанный на “прямом” и “обратном” проектировании. Матрицы-проекторы определяются путем минимизации кросс-энтропийного функционала.
Здесь EDR-метод развивается для параллельного сжатия матрицы данных с учетом их информационной емкости, реализуемого на базе условных энтропийных проекций с детерминированными и рандомизированными матрицами-проекторами. В последнем случае применяется принцип сохранения среднего расстояния между многомерными и маломерными точками в соответствующих пространствах.
6.1. Параллельное детерминированное проектирование с ограничениями информационной емкости (расширенный EDR-метод)
Параллельная реализация процедуры “прямого” и “обратного” проектирования, примененная к матрице данных ${{U}_{{(m \times s)}}} > 0$, приводит к следующей цепочке матричных равенств:
• “прямая” проекция
(6.1)
${{U}_{{(m \times s)}}}{{Q}_{{(s \times r)}}} = {{Y}_{{(m \times r)}}},\quad {{B}_{{(n \times m)}}}{{Y}_{{(m \times r)}}} = {{Z}_{{(n \times r)}}},$• “обратная” проекция
(6.2)
${{Z}_{{(n \times r)}}}{{W}_{{(r \times s)}}} = {{D}_{{(n \times s)}}},\quad {{E}_{{(m \times n)}}}{{D}_{{(n \times s)}}} = {{X}_{{(m \times s)}}}.$Матрицы-проекторы $Q,\;B,\;W,\;E$ – неотрицательные. Равенства (6.1) преобразуют матрицу ${{U}_{{(m \times s)}}}$ в “сжатую” матрицу ${{Z}_{{(n \times r)}}}$, где n < m, r < s. Равенство (6.2) преобразует матрицу ${{Z}_{{(n \times r)}}}$ в матрицу ${{X}_{{m \times s}}}$ той же размерности, что и исходная матрица данных ${{U}_{{(m \times s)}}}$.
Из равенств (6.1)–(6.2) имеем:
(6.3)
${{X}_{{(m \times s)}}} = {{E}_{{(m \times n)}}}\left\{ {\left[ {{{B}_{{(n \times m)}}}\left( {{{U}_{{(m \times s)}}}{{Q}_{{(s \times r)}}}} \right)} \right]{{W}_{{(r \times s)}}}} \right\} > 0.$Скобки в этом равенстве указывают на последовательность операций проектирования: $( \bullet )\, \to \,[ \bullet ]\, \to \,\{ \bullet \} $.
Элементы матрицы-проекции ${{Z}_{{(n \times s)}}}$ имеют вид:
(6.4)
${{z}_{{\mu ,\nu }}} = \sum\limits_{\beta = 1}^m {{b}_{{\mu ,\beta }}}\sum\limits_{\alpha = 1}^r {{u}_{{\beta ,\alpha }}}{\kern 1pt} {{q}_{{\alpha ,\nu }}},\quad \mu = \overline {1,n} ,{\kern 1pt} \quad \nu = \overline {1,r} .$Элементы матрицы ${{X}_{{(m \times s)}}}$ имеют вид:
(6.5)
$\begin{gathered} {{x}_{{ij}}} = \sum\limits_{\mu = 1}^n {{e}_{{i,\mu }}}\sum\limits_{\nu = 1}^r {{w}_{{\nu ,j}}}\sum\limits_{\beta = 1}^m {{b}_{{\mu ,\beta }}}\sum\limits_{\alpha = 1}^s {{u}_{{\beta ,\alpha }}}{{q}_{{\alpha ,\nu }}} > 0, \\ i = \overline {1,m} ,{\kern 1pt} \quad j = \overline {1,s} . \\ \end{gathered} $Для измерения отклонения преобразованной матрицы ${{X}_{{(m \times s)}}}$ от исходной ${{U}_{{(m \times s)}}}$ воспользуемся информационной кросс-энтропией [44]
(6.6)
$\mathcal{H}(X\,{\text{|}}\,U) = \sum\limits_{i = 1}^m \sum\limits_{j = 1}^s {{s}_{{ij}}}(X\,{\text{|}}\,U),$С учетом равенства (6.5) не трудно видеть, что информационная кросс-энтропия (6.6) есть скалярная функция от матрицы данных U > 0 и матриц-проекторов $(Q,B,W,E) \geqslant 0$, т.е.
Важным показателем качества процедуры редукции является оптимальное снижение информационной емкости редуцированной матрицы ${{Z}_{{(n \times r)}}}$ по сравнению с информационной емкостью исходной матрицы данных ${{U}_{{(m \times s)}}}$ [45].
Информационная емкость измеряется в энтропийных терминах:
(6.9)
$\begin{gathered} {{\mathcal{I}}_{Z}} = \sum\limits_{(i,j) = 1}^{n,r} {{z}_{{ij}}}(Q,B)\ln {{z}_{{ij}}}(Q,B) + {{e}^{{ - 1}}}nr, \\ {{\mathcal{I}}_{U}} = \sum\limits_{(i,j) = 1}^{m,s} {{u}_{{ij}}}\ln {{u}_{{ij}}} + {{e}^{{ - 1}}}ms. \\ \end{gathered} $Различие в указанных информационных емкостях будем характеризовать квадратичным функционалом
(6.10)
$\mathcal{J}(Q,B\,{\text{|}}\,U) = {{\left( {\sum\limits_{(i,j) = 1}^{n,r} {{z}_{{ij}}}(Q,B)\ln {{z}_{{ij}}}(Q,B) - A} \right)}^{2}},$Образуем обобщенный функционал
(6.12)
$\mathcal{F}(Q,B,W,E\,{\text{|}}\,U)\, = \,\mathcal{H}(Q,B,W,E\,{\text{|}}\,U)\, + \,\mathcal{J}(Q,B\,{\text{|}}\,U),$(6.13)
$(Q{\kern 1pt} *,B{\kern 1pt} *,W{\text{*}},E{\kern 1pt} *)\, = \,\arg \mathop {\min }\limits_{(Q,B,W,E) \geqslant 0} \mathcal{F}(Q,B,W,E\,{\text{|}}\,U).$Замечание. В задаче (6.13) условие близости информационных емкостей матрицы данных и редуцированной матрицы может быть реализовано в виду соответствующего ограничения. Тогда оптимальные значения неотрицательных элементов матриц-проекторов определяются решением следующей задачи:
(6.14)
$\begin{gathered} (Q{\kern 1pt} *,B{\kern 1pt} *,W{\kern 1pt} *,E{\kern 1pt} *)\, = \,\arg \mathop {\min }\limits_{(Q,B,W,E) \in \Omega } \mathcal{H}(Q,B,W,E\,{\text{|}}\,U), \\ \Omega = \left\{ {(Q,B,W,E):(Q,B,W,E) \geqslant 0;} \right. \\ \left. {{\kern 1pt} {{\mathcal{I}}_{Z}}(Q,B) \geqslant \delta {\kern 1pt} {{\mathcal{I}}_{U}}} \right\},\quad \delta \in (0,1). \\ \end{gathered} $Допустимый уровень снижения информационной емкости редуцированной матрицы регулируется параметром δ.
Алгоритм параллельной редукции. Задача (6.13) является задачей минимизации функционала на неотрицательном ортанте. Для ее решения применим метод проекций градиента, предварительно осуществив векторизацию соответствующих матриц [46].
Введем блочные векторы ${\mathbf{v}} = \{ q,{\mathbf{b}}\} $ и ${\mathbf{c}}\, = \,\{ w,e\} $, каждый размерности
где векторы q, b являются результатами векторизации матриц Q, B, а векторы w, e являются результатами векторизации матриц $W,\;E$ соответственно.Представим (6.13) в следующем виде:
(6.15)
$\begin{gathered} \mathcal{H}({\mathbf{v}},{\mathbf{c}}\,|\,{\mathbf{u}}) = {{\langle {\kern 1pt} {\mathbf{x}}({\mathbf{v}},{\mathbf{c}}),{\mathbf{y}}({\mathbf{v}},{\mathbf{c}}\,|\,{\mathbf{u}})\rangle }_{{{{R}^{{ms}}}}}}, \\ \mathcal{J}({\mathbf{v}}) = {{\langle {\kern 1pt} {\mathbf{z}}({\mathbf{v}}),{\mathbf{g}}({\mathbf{v}})\rangle }_{{{{R}^{{nr}}}}}}, \\ \end{gathered} $Здесь приняты следующие обозначения :
• вектор u – результат векторизации матрицы данных U, размерности (ms); и вектор x, размерности (ms), с компонентами (6.5);
• вектор y, размерности (ms) с компонентами
• вектор g, размерности (nr) с компонентами
В параллельной процедуре вектор v объединяет элементы матриц Q, B, с помощью которых производится “сжатие” матрицы данных по одному измерению. В вектор c входят элементы матриц W, E, с помощью которых производится “сжатие” по второму измерению. Такое разделение векторов удобно для применения по-координатного алгоритма.
Итерационный шаг по-координатной схемы метода проекций градиента состоит из двух последовательно реализуемых этапов: на одном осуществляется итерация по v-проекциям градиента, а на другом – по ${\mathbf{c}}$-проекциям градиента функционала $\mathcal{F}({\mathbf{v}},{\mathbf{c}}\,{\text{|}}\,{\mathbf{u}})$. Обозначим градиенты по этим векторам:
(6.18)
$\begin{gathered} {{\nabla }_{{\mathbf{v}}}}\mathcal{F} = {{\nabla }_{{\mathbf{v}}}}\mathcal{H} + {{\nabla }_{{\mathbf{v}}}}\mathcal{I}, \\ {{\nabla }_{{\mathbf{c}}}}\mathcal{F} = {{\nabla }_{{\mathbf{c}}}}\mathcal{H}. \\ \end{gathered} $Для численного решения этой задачи применим по-координатную схему метода проекций градиента. Алгоритм минимизации функционала $\mathcal{F}$ имеет следующий вид:
a) начальный шаг
б) i-й итерационный шаг
в) условие остановки
6.2. Энтропийно-рандомизированные проекции (REDR-метод)
Рандомизированное проектирование с целью снижения размерности исходной матрицы данных основано на существовании линейного преобразования, мало меняющего среднее расстояние между точками исходного и редуцированного пространств (лемма Джонсона-Линденштраусса [66, 67].
Рассмотрим снова матрицу данных ${{U}_{{(m \times s)}}}$. В пространстве Rs ее отображает множество точек $\mathfrak{A} = \{ {{{\mathbf{u}}}^{{(1)}}}, \ldots ,{{{\mathbf{u}}}^{{(m)}}}\} $. Определим, как это производилось в разделе 5, индикатор этой группы (матрицы-данных) в виде:
(6.19)
${\text{dis}}(U) = \frac{1}{{{{m}^{2}}}}\sum\limits_{(\alpha ,\beta ) = 1}^m \varrho ({{{\mathbf{u}}}^{\alpha }},{{{\mathbf{u}}}^{\beta }}).$Матрицу данных ${{U}_{{(m \times s)}}}$ трансформируем в редуцированную матрицу ${{Z}_{{(n \times r)}}}$, n < m, r < s с помощью случайных, интервальных левых ${{B}_{{(n \times m)}}}$ и правых ${{Q}_{{(s \times r)}}}$ матриц-проекторов:
(6.20)
$\begin{gathered} {{Z}_{{(n \times r)}}} = {{B}_{{(n \times m)}}}{{U}_{{(m \times s)}}}{{Q}_{{(s \times r)}}}, \\ Q \in \mathcal{Q} = [{{Q}^{ - }},{{Q}^{ + }}],\quad B \in \mathcal{B} = [{{B}^{ - }},{{B}^{ + }}]. \\ \end{gathered} $Вероятностные свойства матриц проекторов характеризуются совместной функцией ПРВ $P(Q,B)$ (ПРВ), которая определена на носителе $\mathcal{V}$:
Элементы редуцированной матрицы Z имеют вид:
(6.22)
$\begin{gathered} {{z}_{{\mu ,\nu }}}(Q,B)\, = \,\sum\limits_{\beta = 1}^m {{b}_{{\mu ,\beta }}}\sum\limits_{\alpha = 1}^r {{u}_{{\beta ,\alpha }}}{\kern 1pt} {{q}_{{\alpha ,\nu }}}, \\ \mu \, = \,\overline {1,n} ,\quad \nu \, = \,\overline {1,r} . \\ \end{gathered} $По аналогии с (6.19) определим индикатор редуцированной матрицы ${{Z}_{{(n \times s)}}}$ в виде:
(6.23)
${\text{dis}}(Z(Q,B)) = \frac{1}{{{{n}^{2}}}}\sum\limits_{(\eta ,\kappa ) = 1}^n \varrho ({{{\mathbf{z}}}^{{(\eta )}}}(Q,B),{{{\mathbf{z}}}^{{(\kappa )}}}(Q,B)).$Поскольку элементы матриц-проекторов – случайные, индикатор ${\text{dis}}(Z(Q,B))$ является функцией случайных переменных. Его математическое ожидание
(6.24)
$\begin{gathered} \mathcal{M}\{ {\text{dis}}(Z(Q,B))\} = G[P(Q,B)] = \\ \, = \int\limits_\mathcal{V} P(Q,B){\text{dis}}(Z(Q,B))dQdB. \\ \end{gathered} $Для определения функции ПРВ $P(Q,B)$ будем использовать оценку максимальной энтропии (см. раздел 1):
(6.25)
$\mathcal{H}{\text{[}}\mathcal{P}{\text{(}}\mathcal{Q}{\text{,}}\mathcal{B}{\text{)]}}\, = \, - {\kern 1pt} \int\limits_\mathcal{Z} P(Q,B){\text{ln}}P(Q,B)dQdB\, \Rightarrow \,\max ,$(6.26)
$\begin{gathered} \int\limits_\mathcal{Z} P(Q,B)dQdB = 1; \\ \int\limits_\mathcal{V} P(Q,B){\kern 1pt} {\text{dis}}(Z(Q,B))dQdB = \delta {\kern 1pt} {\text{dis}}(U),{\kern 1pt} \\ 0 < \delta < \theta < 1. \\ \end{gathered} $Задача (6.25)–(6.26) относится к классу ляпуновских задач [48], для которых условия оптимальности формулируются в терминах стационарности функционала Лагранжа
(6.27)
$\begin{gathered} \mathcal{L}[P(Q,B),\lambda ] = \\ \, = \mathcal{H}{\text{[}}\mathcal{P}{\text{(}}\mathcal{Q}{\text{,}}\mathcal{B}{\text{)]}} + \lambda \left( {\delta {\kern 1pt} {\text{dis}}(U) - G[P(Q,B)]} \right), \\ \end{gathered} $Получим энтропийно-оптимальную ПРВ
(6.28)
$P{\kern 1pt} {\text{*}}(Q,B) = \frac{{\exp \left( { - \lambda {\kern 1pt} {\text{dis}}(Z(Q,B))} \right)}}{{\mathcal{P}(\lambda )}},$(6.29)
$\mathcal{P}(\lambda ) = \int\limits_\mathcal{Z} \exp \left( { - \lambda {\kern 1pt} {\text{dis}}(Z(Q,B))} \right){\kern 1pt} dQdB.$Множитель Лагранжа λ определяется из следующего уравнения:
(6.30)
$\begin{gathered} \int\limits_\mathcal{V} \exp \left( { - \lambda {\kern 1pt} {\text{dis}}(Z(Q,B))} \right) \times \\ \, \times \left( {{\text{dis}}(Z(Q,B)) - \delta {\kern 1pt} {\text{dis}}(U))} \right){\kern 1pt} dQdB = 0. \\ \end{gathered} $Таким образом, энтропийно-оптимальная функция ПРВ $P{\kern 1pt} {\text{*}}(Q,B)$ (6.28) позволяет, путем ее сэмплирования, генерировать матрицы-проекторы Q, B, сохраняющие “в среднем” расстояние между точками (векторами ${{{\mathbf{z}}}^{{(\alpha )}}}$) редуцированной матрицы $\mathcal{Z}$.
6.3. Рандомизированные матрицы-проекторы с заданными значениями элементов
Рассмотрим матрицу данных ${{U}_{{(m \times s)}}}$, которую нужно “сжать” по переменной s до размера r:
Матрица ${{U}_{{(m \times s)}}} \geqslant 0$ и имеет нормированные элементы ($0 \leqslant {{u}_{{ij}}} \leqslant 1$). Определим индикатор редуцированной матрицы ${{Y}_{{(m \times r)}}}$ в виде:
(6.32)
${\text{dis}}(Y(Q)) = \frac{1}{{{{m}^{2}}}}\sum\limits_{(i,j) = 1}^m {\kern 1pt} \rho ({{{\mathbf{y}}}^{{(i)}}}(Q),{{{\mathbf{y}}}^{{(j)}}}(Q)).$Рассмотрим случай, когда элементы матрицы ${{Q}_{{(s \times r)}}}$ могут принимать значения 0 или 1, и размещение их в матрице – случайное. Количество различных матриц такого типа равно $N{{ = 2}^{{rs}}}$:
Полагая, что реализации – случайные, их вероятностные свойства будем характеризовать дискретной функцией распределения вероятностей (ДРВ)
Математическое ожидание индикатора (6.32)
(6.35)
$\mathcal{M}\{ {\text{dis}}(Y(Q))\} = \sum\limits_{a = 1}^N {{w}_{a}}{\text{dis}}(Y({{Q}^{a}})).$Функцию ДРВ W(a) будем искать в классе функций, максимизирующих функцию информационной энтропии Ферми [49]:
(6.36)
$\begin{gathered} {{H}_{F}}({\mathbf{w}}) = - \sum\limits_{a = 1}^N {{w}_{a}}\ln {{w}_{a}} + \\ \, + (1 - {{w}_{a}})\ln (1 - {{w}_{a}}) \Rightarrow \max , \\ \end{gathered} $(6.37)
$\sum\limits_{a = 1}^N {{w}_{a}}{\kern 1pt} {\text{dis}}(Y({{Q}^{a}})) = \delta {\kern 1pt} {\text{dis}}(U),\quad 0 < \varepsilon \leqslant \delta \leqslant 1.$Задача (6.36)–(6.37) является конечно-мерной задачей максимизации с вогнутой целевой функцией и нелинейным ограничением.
Рассмотрим функцию Лагранжа
(6.38)
$\begin{gathered} L({\mathbf{w}},\lambda ) = {{H}_{F}}({\mathbf{w}}) + \\ \, + \lambda \left( {\delta {\kern 1pt} {\text{dis}}(U) - \sum\limits_{a = 1}^N {{w}_{a}}{\text{dis}}(Y({{Q}^{a}}))} \right). \\ \end{gathered} $Условия стационарности этой функции имеют вид:
(6.39)
$\begin{gathered} \frac{{\partial L}}{{\partial {{w}_{a}}}} = - {\text{ln}}\frac{{{{w}_{a}}}}{{1 - {{w}_{a}}}}\, - \,\lambda {\text{dis}}(Y({{Q}^{a}}))\, = \,0,\quad a\, = \,\overline {1,N} ; \\ \frac{{\partial L}}{{\partial \lambda }} = \left( {\delta {\kern 1pt} {\text{dis}}(U) - \sum\limits_{a = 1}^N {{w}_{a}}{\text{dis}}(Y({{Q}^{a}}))} \right) = 0. \\ \end{gathered} $Отсюда получаем, что энтропийно-оптимальное распределение вероятностей имеет вид:
(6.40)
$w_{a}^{*} = \frac{{\exp ( - \lambda {\kern 1pt} {\text{dis}}(Y({{Q}^{a}}))))}}{{1 + \exp ( - \lambda {\kern 1pt} {\text{dis}}(Y({{Q}^{a}})))}},\quad a = \overline {1,N} ,$(6.41)
$\sum\limits_{a = 1}^N \frac{{\exp ( - \lambda {\kern 1pt} {\text{dis}}(Y({{Q}^{a}})))){\kern 1pt} {\text{dis}}(Y({{Q}^{a}}))}}{{1 + \exp ( - \lambda {\kern 1pt} {\text{dis}}(Y({{Q}^{a}})))}} = \delta {\kern 1pt} {\text{dis}}(U).$Таким образом, равенство (6.40) определяет распределение вероятностей матриц-проекторов с элементами {0, 1}. Имеет смысл выбрать матрицу-проектор
хотя возможны и другие стратегии.7. ПРИКЛАДНЫЕ ЗАДАЧИ И ИЛЛЮСТРАТИВНЫЕ ПРИМЕРЫ
7.1. Рандомизированная бинарная классификация
Проблема классификации объектов является весьма актуальной в современной теоретической и прикладной науке. При рандомизированной бинарной классификации (РБК) применяется модель решающего правила со случайными параметрами, оценки функции ПРВ которых определяются путем ЭРО-оценивания (см. раздел 3) с учетом обучающих последовательностей данных. Принципиальное отличие РБК от существующих процедур состоит в генерации эмпирической функции принадлежности классам обученной на реальных данных.
7.1.1. Процедура РБК
1. Структура обучающих данных. Пусть имеется обучающая коллекция из $n$ объектов, характеризуемых векторами $\{ {{{\mathbf{e}}}^{{(1)}}}, \ldots ,{{{\mathbf{e}}}^{{(n)}}}\} $ из признакового пространства ${{R}^{m}}$ и вектором-ответов ${\mathbf{y}} = \{ 0,1$, ..., 1}. Этот вектор размерности n, и его компоненты 0 и 1 являются метками принадлежности объекта классу 1 (“1”), или классу 2 (“0”).
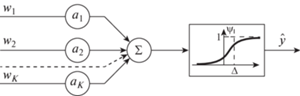
2. Модель решающего правила. Используем однослойную нейронную сеть с сигмоидной функцией активации [63]:
(7.1)
${{\hat {y}}^{{(i)}}}({\mathbf{a}}) = {\text{sigm}}{\kern 1pt} (\langle {{{\mathbf{E}}}^{{(i)}}},{\mathbf{b}}\rangle ),\quad i = \overline {1,n} ,$(7.2)
$\begin{gathered} {\text{sigm}}({{x}_{i}}) = \frac{1}{{1 + \exp [ - \alpha ({{x}_{i}} - \Delta )]}}, \\ {{x}_{i}} = (\langle {{{\mathbf{E}}}^{{(i)}}},{\mathbf{b}}\rangle ), \\ {\mathbf{a}} = \{ {\mathbf{b}},\alpha ,\Delta \} . \\ \end{gathered} $На рис. 2 показан график сигмоидной функции с параметрами “крутизны” α и “порога” $\Delta $. Значения функции ${\text{sigm}}(x)$ в интервале $\left[ {\frac{1}{2},1} \right]$ соответствуют первому классу, и значения в интервале $\left[ {0,\frac{1}{2}} \right]$ – второму классу.
В рандомизированной модели (7.1), (7.2) параметры ${\mathbf{a}} = \{ {{a}_{1}}, \ldots ,{{a}_{{(n + 2)}}}\} $ – интервального типа:
(7.3)
$\begin{gathered} {{a}_{k}} \in {{\mathcal{A}}_{k}} = [a_{k}^{ - },a_{k}^{ + }],\quad k = \overline {1,n + 2} , \\ \mathcal{A} = \bigcup\limits_{k = 1}^{n + 2} {{\mathcal{A}}_{k}}. \\ \end{gathered} $Их вероятностные свойства характеризуются PDF $P({\mathbf{a}})$, которая определена на множестве $\mathcal{A}$.
Итак, алгоритм рандомизированной бинарной классификации представляется в следующем виде:
(7.4)
$\mathcal{H}[P({\mathbf{a}})] = - \int\limits_\mathcal{A} P({\mathbf{a}}){\kern 1pt} \ln P({\mathbf{a}})d{\mathbf{a}} \Rightarrow \max ,$(7.6)
$\int\limits_\mathcal{A} P({\mathbf{a}}){\kern 1pt} {{\hat {y}}^{i}}({\mathbf{a}}){\kern 1pt} d{\mathbf{a}} = {{y}_{i}},\quad i = \overline {1,h} .$Энтропийно-оптимальная ПРВ
(7.7)
$P{\kern 1pt} {\text{*}}({\mathbf{a}}{\kern 1pt} |{\kern 1pt} \theta ) = \frac{{\exp \left[ { - \sum\limits_{i = 1}^h {{\theta }_{i}}{{{\hat {y}}}^{{(i)}}}({\mathbf{a}})\rangle } \right]}}{{\mathcal{P}(\theta )}},$(7.8)
$\mathcal{P}(\theta ) = \int\limits_\mathcal{A} \exp \left[ { - \sum\limits_{i = 1}^h {{\theta }_{i}}{{{\hat {y}}}^{{(i)}}}({\mathbf{a}})} \right].$Множители Лагранжа определяются из уравнений (7.6).
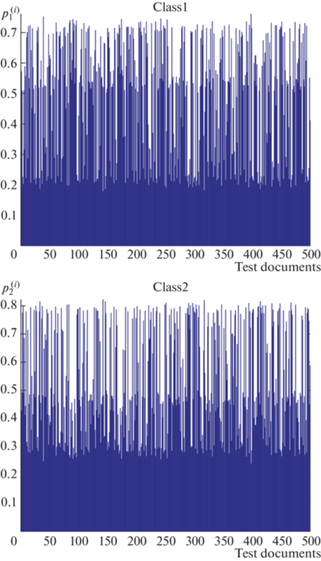
3. Реализация рандомизированной бинарной классификации. Рассмотрим коллекцию из M объектов, характеризуемых векторами t(i), $i = \overline {1,M} $ и подлежащих бинарной классификации. Воспользуемся найденной энтропийно-оптимальной функцией ПРВ $P{\kern 1pt} {\text{*}}({\mathbf{a}})$ модели решающего правила (7.1) для определения эмпирических вероятностей принадлежности объекта k классу 1 или 2. Обозначим эти вероятности $p_{1}^{{(k)}}$ и $p_{2}^{{(k)}}$ соответственно, k = $\overline {1,M} $.
Функция ПРВ $P({\mathbf{a}})$ сэмплируется, т.е. генерируется модифицированным методом Монте-Карло соответствующая последовательность случайных векторов-параметров модели ${{{\mathbf{a}}}^{{(i)}}},{\kern 1pt} i = \overline {1,N} $, где N – количество МК-испытаний. Пусть в результате этих испытаний оказалось, что первый объект N1 раз был отнесен к первому классу и $N - {{N}_{1}}$ раз – ко второму; …., k-й объект ${{N}_{k}}$ раз отнесен к первому классу и $N - {{N}_{k}}$ раз – ко второму классу, и т.д. При достаточно большом числе испытаний определяются эмпирические вероятности принадлежности
Если требуется “жесткий” вариант классификации, то необходимо задать порог δ вероятности, и считать объекты, вероятность принадлежности которых превышает порог, относящимися к соответствующему классу. В результате “жесткой” классификации возникает вектор ${\mathbf{u}} = \{ 0,1,1$, ..., 1}, номер компоненты которого соответствует номеру объекта, а 0 или 1 отображает принадлежность его классу 1 или 2.
Далее мы воспользуемся этим вектором для оценки точности “жесткой” классификации, выполненной рандомизированной бинарной процедурой.
7.1.2. Модельные примеры
1. Рандомизированная классификация четырехмерных объектов. Рассмотрим объекты, характеризуемые 4 признаками.
1.1. Обучение. Обучающая коллекция состоит из трех объектов, значения признаков которых показаны в табл. 1.
Таблица 1
| i | $e_{1}^{{(i)}}$ | $e_{2}^{{(i)}}$ | $e_{3}^{{(i)}}$ | $e_{4}^{{(i)}}$ |
|---|---|---|---|---|
| 1 | 0.11 | 0.75 | 0.08 | 0.21 |
| 2 | 0.91 | 0.65 | 0.11 | 0.81 |
| 3 | 0.57 | 0.17 | 0.31 | 0.91 |
Рандомизированная модель решающего правила (7.1), (7.2) имеет параметры: $\alpha = 1,0$ и $\Delta = 0$. Выход модели ${\mathbf{\hat {y}}} = \{ 0,18;{\kern 1pt} \,0,81;{\kern 1pt} \,0,43\} $ (${{y}_{i}} < 0,5$ соответствует классу 2, ${{y}_{i}} \geqslant 0,5$ соответствует классу 1).
Множители Лагранжа для энтропийно-оптимальной PDF (7.7) имеют следующие значения: $\bar {\theta }{\kern 1pt} * = \{ 0.2524;1.7678$; 1.6563}. Параметры ${{a}_{j}} \in [ - 10$, 10], $j = \overline {1,4} $. Энтропийно-оптимальная для данной обучающей коллекции функция PDF имеет вид:
(7.9)
$\begin{gathered} P{\kern 1pt} {\text{*}}({\mathbf{a}},\bar {\theta }) = \frac{{\exp \left( { - \sum\limits_{i = 1}^3 {{\theta }_{i}}{{y}_{i}}({\mathbf{a}})} \right)}}{{\mathcal{P}(\bar {\theta })}}, \\ {{y}_{i}}({\mathbf{a}}) = {{\left( {1 + \exp \left( { - \sum\limits_{k = 1}^4 e_{k}^{{(i)}},{{a}_{k}}} \right)} \right)}^{{( - 1)}}}. \\ \end{gathered} $На рис. 3 показано двумерное сечение PDF P*(a, $\bar {\theta }{\kern 1pt} *)$.
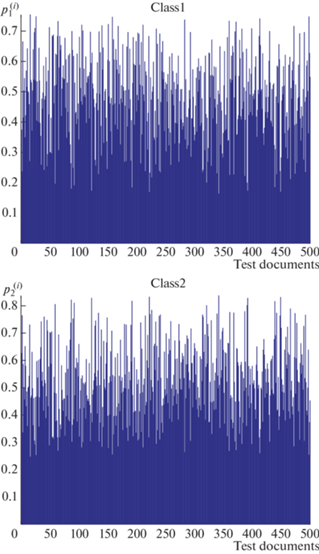
1.2. Реализация. На этом этапе используется коллекция из r модельных объектов, где каждый объект характеризуется вектором ${{{\mathbf{t}}}^{{(j)}}} \in {{R}^{{(4)}}}$. Генерируется массив (500 × 4) четырехмерных случайных, независимых векторов ${{{\mathbf{t}}}^{{(i)}}},{\kern 1pt} i = \overline {1,500} $ с независимыми компонентами, равномерно распределенными в интервалах [0, 1]. Далее применяется процедура рандомизированной бинарной классификации. На рис. 4 показаны эмпирические вероятности $p_{1}^{{(i)}},p_{2}^{{(i)}}$ принадлежности ti-объекта классу 1 и 2.
2. Рандомизированная классификация двумерных объектов. Рассмотрим объекты, характеризуемые 2 признаками.
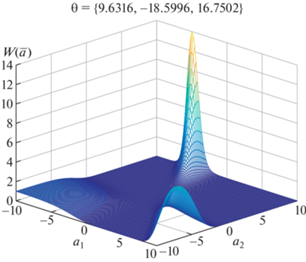
2.1. Обучение. Обучающая коллекция состоит из трех объектов, каждый из которых описывается двумя признаками, значения которых показаны в табл. 2. Значения параметров $\alpha ,\Delta $ и интервалов для случайных параметров a соответствуют примеру 1. Множители Лагранжа для энтропийно-оптимальной PDF (7.7) имеют следующие значения: $\bar {\theta }{\kern 1pt} * = \{ 9.6316; - 18.5996$; 16.7502}. Энтропийно-оптимальная для данной обучающей коллекции функция $P{\text{*}}({\mathbf{a}}{\kern 1pt} |{\kern 1pt} \bar {\theta })$ имеет вид:
(7.10)
$\begin{gathered} P{\kern 1pt} {\text{*}}({\mathbf{a}}) = \frac{{\exp \left( { - \sum\limits_{i = 1}^3 {{\theta }_{i}}{{y}_{i}}({\mathbf{a}})} \right)}}{{\mathcal{P}(\bar {\theta })}}, \\ {{y}_{i}}({\mathbf{a}}) = {{\left( {1 + \exp \left( { - \sum\limits_{k = 1}^2 e{{{(i)}}_{k}},{{a}_{k}}} \right)} \right)}^{{( - 1)}}}. \\ \end{gathered} $Таблица 2.
Матрица данных
| № | ${{x}_{1}}$ | ${{x}_{2}}$ | Вид | № | ${{x}_{1}}$ | ${{x}_{2}}$ | Вид | № | ${{x}_{1}}$ | ${{x}_{2}}$ | Вид |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.5 | 1.5 | 2 | 8 | 3.9 | 1.4 | 2 | ||||
| 2 | 4.6 | 1.5 | 2 | 9 | 4.5 | 1.3 | 2 | 15 | 1.4 | 0.2 | 1 |
| 3 | 4.7 | 1.4 | 2 | 10 | 4.6 | 1.3 | 2 | 16 | 1.5 | 0.2 | 1 |
| 4 | 1.7 | 0.4 | 1 | 11 | 1.4 | 0.2 | 1 | 17 | 1.5 | 0.1 | 1 |
| 5 | 1.3 | 0.2 | 1 | 12 | 4.7 | 1.6 | 2 | 18 | 4.9 | 1.5 | 2 |
| 6 | 1.4 | 0.3 | 1 | 13 | 4.0 | 1.3 | 2 | 19 | 3.3 | 1.0 | 2 |
| 7 | 1.5 | 0.2 | 1 | 14 | 1.4 | 0.2 | 1 | 20 | 1.4 | 0.2 | 1 |
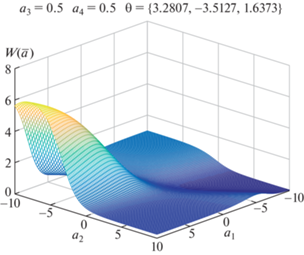
На рис. 5 показана функция $P{\kern 1pt} {\text{*}}({\mathbf{a}},\bar {\theta }{\text{*}})$.
Рис. 5.
Энтропийно-оптимальная PDF $P{\kern 1pt} {\text{*}}({\mathbf{a}},\bar {\theta }{\kern 1pt} *)$.
2.2. Реализация. Все параметры этого примера соответствуют примеру 2. На рис. 6 показаны эмпирические вероятности $p_{1}^{{(i)}},\;p_{2}^{{(i)}}$ принадлежности ti-го объекта классу 1 и 2 ($i = \overline {1,500} $).
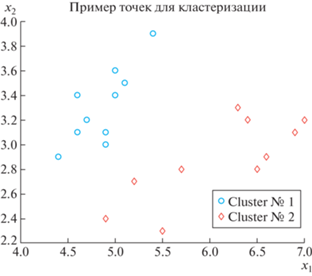
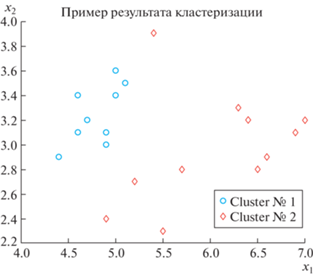
7.2. Рандомизированная кластеризация биологичеких объектов
Рассмотрим бинарную кластеризацию цветков ириса, используя базу Fisheriris (цветки ириса: ширина ${{x}_{1}}$ и длина ${{x}_{2}}$ лепестков). База содержит данные по указанным признакам трех видов цветков: “setosa” (1), “versicolor” (2), “virginica” (3), в количестве 50-ти двумерных точек на каждый вид. Далее будем рассматривать два вида (1, 2) и по 10 данным на каждый вид. В иллюстративных примерах удобнее представлять характеристики цветков в матричном виде.
Пример 1
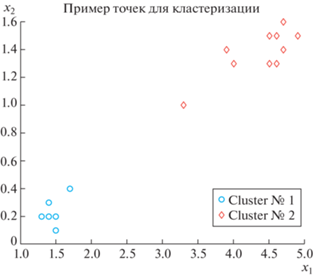
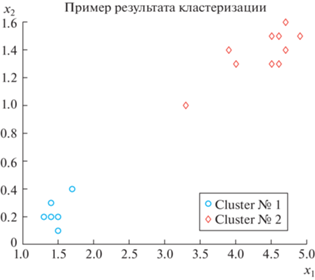
Матрица данных содержит числовые значения двух признаков для 1-го и 2-го видов и представлена в табл. 2.
На рис. 7 показано расположение объектов-точек на плоскости.
Матрица расстояний ${{D}_{{(20 \times 20)}}}$ показана в табл. 3, 4.
Таблица 3.
Матрица расстояний для матрицы данных
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.1 | 0.22 | 3.01 | 3.45 | 3.32 | 3.27 | 0.61 | 0.2 | 0.22 |
| 2 | 0.1 | 0 | 0.14 | 3.1 | 3.55 | 3.42 | 3.36 | 0.71 | 0.22 | 0.2 |
| 3 | 0.22 | 0.14 | 0 | 3.16 | 3.61 | 3.48 | 3.42 | 0.8 | 0.22 | 0.14 |
| 4 | 3.01 | 3.1 | 3.16 | 0 | 0.45 | 0.32 | 0.28 | 2.42 | 2.94 | 3.04 |
| 5 | 3.45 | 3.55 | 3.61 | 0.45 | 0 | 0.14 | 0.2 | 2.86 | 3.38 | 3.48 |
| 6 | 3.32 | 3.42 | 3.48 | 0.32 | 0.14 | 0 | 0.14 | 2.73 | 3.26 | 3.35 |
| 7 | 3.27 | 3.36 | 3.42 | 0.28 | 0.2 | 0.14 | 0 | 2.68 | 3.2 | 3.29 |
| 8 | 0.61 | 0.71 | 0.8 | 2.42 | 2.86 | 2.73 | 2.68 | 0 | 0.61 | 0.71 |
| 9 | 0.2 | 0.22 | 0.22 | 2.94 | 3.38 | 3.26 | 3.2 | 0.61 | 0 | 0.1 |
| 10 | 0.22 | 0.2 | 0.14 | 3.04 | 3.48 | 3.35 | 3.29 | 0.71 | 0.1 | 0 |
| 11 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
| 12 | 0.22 | 0.14 | 0.2 | 3.23 | 3.68 | 3.55 | 3.49 | 0.82 | 0.36 | 0.32 |
| 13 | 0.54 | 0.63 | 0.71 | 2.47 | 2.92 | 2.79 | 2.73 | 0.14 | 0.5 | 0.6 |
| 14 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
| 15 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
| 16 | 3.27 | 3.36 | 3.42 | 0.28 | 0.2 | 0.14 | 0 | 2.68 | 3.2 | 3.29 |
| 17 | 3.31 | 3.4 | 3.45 | 0.36 | 0.22 | 0.22 | 0.1 | 2.73 | 3.23 | 3.32 |
| 18 | 0.4 | 0.3 | 0.22 | 3.38 | 3.83 | 3.7 | 3.64 | 1 | 0.45 | 0.36 |
| 19 | 1.3 | 1.39 | 1.46 | 1.71 | 2.15 | 2.02 | 1.97 | 0.72 | 1.24 | 1.33 |
| 20 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
Таблица 4.
Матрица расстояний для матрицы данных (продолжение)
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.1 | 0.22 | 3.01 | 3.45 | 3.32 | 3.27 | 0.61 | 0.2 | 0.22 |
| 2 | 0.1 | 0 | 0.14 | 3.1 | 3.55 | 3.42 | 3.36 | 0.71 | 0.22 | 0.2 |
| 3 | 0.22 | 0.14 | 0 | 3.16 | 3.61 | 3.48 | 3.42 | 0.8 | 0.22 | 0.14 |
| 4 | 3.01 | 3.1 | 3.16 | 0 | 0.45 | 0.32 | 0.28 | 2.42 | 2.94 | 3.04 |
| 5 | 3.45 | 3.55 | 3.61 | 0.45 | 0 | 0.14 | 0.2 | 2.86 | 3.38 | 3.48 |
| 6 | 3.32 | 3.42 | 3.48 | 0.32 | 0.14 | 0 | 0.14 | 2.73 | 3.26 | 3.35 |
| 7 | 3.27 | 3.36 | 3.42 | 0.28 | 0.2 | 0.14 | 0 | 2.68 | 3.2 | 3.29 |
| 8 | 0.61 | 0.71 | 0.8 | 2.42 | 2.86 | 2.73 | 2.68 | 0 | 0.61 | 0.71 |
| 9 | 0.2 | 0.22 | 0.22 | 2.94 | 3.38 | 3.26 | 3.2 | 0.61 | 0 | 0.1 |
| 10 | 0.22 | 0.2 | 0.14 | 3.04 | 3.48 | 3.35 | 3.29 | 0.71 | 0.1 | 0 |
| 11 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
| 12 | 0.22 | 0.14 | 0.2 | 3.23 | 3.68 | 3.55 | 3.49 | 0.82 | 0.36 | 0.32 |
| 13 | 0.54 | 0.63 | 0.71 | 2.47 | 2.92 | 2.79 | 2.73 | 0.14 | 0.5 | 0.6 |
| 14 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
| 15 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
| 16 | 3.27 | 3.36 | 3.42 | 0.28 | 0.2 | 0.14 | 0 | 2.68 | 3.2 | 3.29 |
| 17 | 3.31 | 3.4 | 3.45 | 0.36 | 0.22 | 0.22 | 0.1 | 2.73 | 3.23 | 3.32 |
| 18 | 0.4 | 0.3 | 0.22 | 3.38 | 3.83 | 3.7 | 3.64 | 1 | 0.45 | 0.36 |
| 19 | 1.3 | 1.39 | 1.46 | 1.71 | 2.15 | 2.02 | 1.97 | 0.72 | 1.24 | 1.33 |
| 20 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 2.77 | 3.29 | 3.38 |
Минимальный и максимальный элементы:
Ансамбль возможных кластеров имеет объем $K(10)$ = 184 786. Кластер с номером $k = 256,{{i}_{1}} = 1$, i2 = 2, i3 = 3, i4 = 4, i5 = 5, i6 = 6, ${{i}_{7}} = 7,{{i}_{8}} = 14$, i9 = 15, i10 = 20. Матрица расстояний $D_{{(10)}}^{{(256)}}$ приведена в табл. 5.
Таблица 5.
Матрица расстояний для кластера $\mathcal{K}(256)$
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.1 | 0.22 | 3.01 | 3.45 | 3.32 | 3.27 | 3.36 | 3.36 | 3.36 |
| 2 | 0.1 | 0 | 0.14 | 3.1 | 3.55 | 3.42 | 3.36 | 3.45 | 3.45 | 3.45 |
| 3 | 0.22 | 0.14 | 0 | 3.16 | 3.61 | 3.48 | 3.42 | 3.51 | 3.51 | 3.51 |
| 4 | 3.01 | 3.1 | 3.16 | 0 | 0.45 | 0.32 | 0.28 | 0.36 | 0.36 | 0.36 |
| 5 | 3.45 | 3.55 | 3.61 | 0.45 | 0 | 0.14 | 0.2 | 0.1 | 0.1 | 0.1 |
| 6 | 3.32 | 3.42 | 3.48 | 0.32 | 0.14 | 0 | 0.14 | 0.1 | 0.1 | 0.1 |
| 7 | 3.27 | 3.36 | 3.42 | 0.28 | 0.2 | 0.14 | 0 | 0.1 | 0.1 | 0.1 |
| 8 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 |
| 9 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 |
| 10 | 3.36 | 3.45 | 3.51 | 0.36 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 |
Таблица 6.
Матрица данных
| № | ${{x}_{1}}$ | ${{x}_{2}}$ | Вид | № | ${{x}_{1}}$ | ${{x}_{2}}$ | Вид | № | ${{x}_{1}}$ | ${{x}_{2}}$ | Вид |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.4 | 3.2 | 2 | 8 | 5.2 | 2.7 | 2 | ||||
| 2 | 6.5 | 2.8 | 2 | 9 | 5.7 | 2.8 | 2 | 15 | 4.9 | 3.0 | 1 |
| 3 | 7.0 | 3.2 | 2 | 10 | 6.6 | 2.9 | 2 | 16 | 5.0 | 3.4 | 1 |
| 4 | 5.4 | 3.9 | 1 | 11 | 5.1 | 3.5 | 1 | 17 | 4.9 | 3.1 | 1 |
| 5 | 4.7 | 3.2 | 1 | 12 | 6.3 | 3.3 | 2 | 18 | 6.9 | 3.1 | 2 |
| 6 | 4.6 | 3.4 | 1 | 13 | 5.5 | 2.3 | 2 | 19 | 4.9 | 2.4 | 2 |
| 7 | 4.6 | 3.1 | 1 | 14 | 4.4 | 2.9 | 1 | 20 | 5.0 | 3.6 | 1 |
Индикатор матрицы $X_{{(10)}}^{{(256)}}$, соответствующей кластеру $\mathcal{K}_{{(10)}}^{{(256)}}$,
Значения индикаторов для кластеров от k = 1 до $k = 184786$ показаны на рис. 8.
Энтропийно-оптимальная функция распределения вероятностей для s = 10 имеет вид:
(7.13)
$\begin{gathered} p{\kern 1pt} {\text{*}}(k\,{\text{|}}\,10) = \frac{{\exp ( - \lambda {\kern 1pt} {\text{*dis}}(X_{{(10)}}^{{(k)}}))}}{{1 + \exp ( - \lambda {\kern 1pt} {\text{*dis}}(X_{{(10)}}^{{(k)}}))}}, \\ \lambda {\kern 1pt} {\text{*}} = 12.1153. \\ \end{gathered} $Кластер ${{\mathcal{K}}_{1}}$ с максимальной вероятностью имеет номер
(7.14)
$\begin{gathered} k{\kern 1pt} * = 166922, \\ {{\mathcal{K}}_{1}} = \{ 4,5,6,7,11,14,15,16,17,20\} , \\ {\kern 1pt} {\text{dis}}{\kern 1pt} {{\mathcal{K}}_{1}} = 0.1354. \\ \end{gathered} $Кластер ${{\mathcal{K}}_{2}}$ образует следующие объекты-точки: $\{ 1,2,3,8,9,10,12,13,18,19\} $.
Расположение кластеров ${{\mathcal{K}}_{1}}$ и ${{\mathcal{K}}_{2}}$ показано на рис. 9.
Сравнивая с рис. 7, видно, что совпадение 10/10, т.е. ошибка кластеризации равна нулю.
Пример 2
Рассмотрим другую матрицу данных из той же базы. Расположение объектов-точек показано на рис. 10.
Построим матрицу расстояний ${{D}_{{(20 \times 20)}}}$ и определим минимальны и максимальный элементы:
Ансамбль возможных кластеров имеет объем $K(10) = 184\,786$. Значения индикаторов для кластеров от k = 1 до $k = 184\,786$ показаны на рис. 11.
Энтропийно-оптимальная функция распределения вероятностей для s = 10 имеет вид:
(7.16)
$p{\kern 1pt} {\text{*}}(k\,{\text{|}}\,10) = \frac{{\exp ( - \lambda {\kern 1pt} {\text{*dis}}(X_{{(10)}}^{{(k)}}))}}{{1 + \exp ( - \lambda {\kern 1pt} {\text{*dis}}(X_{{(10)}}^{{(k)}}))}},\quad \lambda {\kern 1pt} * = 100.$Кластер ${{\mathcal{K}}_{1}}$ с максимальной вероятностью имеет номер
(7.17)
$\begin{gathered} k{\kern 1pt} * = 177\,570, \\ {{\mathcal{K}}_{1}} = \{ 5,6,7,8,11,14,15,16,17,20\} , \\ {\text{dis}}{\kern 1pt} {{\mathcal{K}}_{1}} = 0.4420. \\ \end{gathered} $Его образуют следующие объекты-точки: 5, 6, 7, $8,11,14,15$, 16, 17, 20. Кластер ${{\mathcal{K}}_{2}}$ образуют следующие объекты-точки: $1,2,3,4,9,10,12,13,18,19$.
Расположение кластеров ${{\mathcal{K}}_{1}}$ и ${{\mathcal{K}}_{2}}$ показано на рис. 12. Сравнивая с рис. 7, видно, что совпадение 8/10.
Список литературы
Boltzmann L. Vorlesungen uber Gastheory. Leipzig, 1896. V. 1, J.A. Barth; 1898. V. 2, J.A. Barth.
Jaynes E.T. Gibbs vs Boltzmann entropy. American Journal of Physics. 1965. V. 33. P. 391–398.
Shannon C.E. Mathematical Theory of Communication. 1948, The Bell System Technical Journal. V. 27. P. 373–423, 623–656, July, Oct.
Renyi A. Probability Theiry, North Holland, Amsterdam, 1970.
Bashkirov A.G. Renyi-entropy is statistical entropy for a large scale systems, Theoretical and Mathematicol Physics., 2006. V. 149. № 2. P. 299–317.
Jaynes E.T. Information theory and statistical Mechanics. Physical Review, 1957. V. 104(4). P. 620–630.
Rosenkrantz R.D., Jaynes E.T. Paper on Probability, Statistics,and Statistical Physics. Kluwer Academic Pablishers, 1989.
Jaynes E.T. Probability theory: the logic of science. Cambridge Uni. Press, 2003.
Schulz K.F., Grimes D.A. Generation of allocation sequences in randomized trials. The Lancet, 2002, Feb. 09. https://doi.org/10.1016/S0140-6736(02)07683-3
Maravelakis P. The use of Statistics in Social Sciences. Journal of Humanities and Applied Social Sciences. 2019. V. 1. № 2. P. 87–97.https://doi.org/10.1108/JHASS-08-2019-0038
Bonaccorsi A., Cicero T., Ferraro A., Malgarini M. Journal raiting as predictors of articles quality in Arts, Humanities and Social Sciences: an analysis based on the Italian Research Evaluation Exercise. F1000. 2015, 4:196. P. 1–12.
Gauvin L., Genois M., Karsal M., Kivela M., Takaguchi T., Valdano E., Vesterguard C.L. Randomized reference models for temporal network. 2020, arXiv: 1806.04032v3[physics.soc-ph], 11 Feb.
Vovk V., Shafer G. Good randomized sequential probability forecasting is always possible. Journal of Royal Statistical Society B. 2005. V. 65. Pt. 5. P. 747–763.
Vyugin V. On calibration error of randomized forecasting algorithm. theoretical Computer Science. 2009. V. 410. P. 1781–1795.
Zhao S., Ma T., Ermon S. Indsividual Calibration with Randomized Forecasting. 2020, arXiv:2006.10288v3 [stat.ML]9 Sept 2020.
Mancini T., Calvo-Pardo H., Olmo J. Extremly randomized neural networks for constructing prediction interval. Neural Networks. 2021. V. 144. P. 113–128.
Motwani R., Raghaven P. Randomized Algorithms. Cambridge Uni. Press, NY, 1995.
Vidyasagar M. Randomized Algorithms for robust controller synthesis using statistical learning theory. Automatica. 2001. V. 37(10). P. 1515–1528.
Tempo R., Calafiory G., Dabbene F. Randomized Algorithms for Analysis and Control of Uncertain Systems, Springer, 2013.
Granichin O., Volkovich Z., Toledano-Kitai D. Randomized Algorithms in Automatic Control and Data Mining. Springer, 2015.
Osborn M.J., Rubinstein A. A Course in Game Theory. 1994, Cambridge, MA, MIT Press.
Borovkov A.A. Mathematical Statistics. CTC Press, 1999.
Larsen R.J., Marx M.L. An Introduction to Mathematical Statistics. 2012, Prentice Hall.
Avellaneda M. Minimum relative-entropy calibration of asset-pricing model. Journal of theoretical and applied finance. 1998. V. 1(04). P. 447–472.
Popkov A.Yu., Popkov Yu.S. New Methods of Entropy-Robust Estimation for Randomized Models under Limited Data // Entropy. 2014. № 16. P. 675–698. https://doi.org/10.3390/e16020675
Ioffe A.D., Tikhomirov V.M. Theory of extremal problems. Elsevier North Holland. 1979. P. 456.
Alexeev V.M., Tikhomirov V.M., Fomin S.V. Optimal Control. Springer-Verlag, Boston, MA. 1987. P. 277.
Voevodin V.V., Kuznetzov Yu.A. Matrices and Computing. Nauka, Moscow, 1984.
Kaashoek M.A., van der Mee Cornelis Recent Advances in Operator Theory and Its Applications, Springer Science & Business Media, 2006. V. 160.
Parr R.G., Yang W. Density-functional Theory of Atoms and Molecules. NY, Oxford Uni Press. 1989.
Coulson T. et al. Estimating the functional form for the density dependence from life history data. Ecology. 2008. V. 89(6). P. 1661–1674.
Beckman M. On the distribution of urban rent and residential density. Journal of Economic Theory, 1969. V. 1. P. 60–67.
Abrams P.A. Determining the functional form of density Dependence: Deduction Approaches for Cosumer-Resource Systems. American Naturalist. 2009. V. 179. № 3. P. 321–330.
Hyvarinen A. Estimation of unnormalized statistical models by score matching. Journal of Machine Learning Research. 2005. V. 6. P. 695–709.
Gutman M.U., Hyvarinen A. Noise-constrastive estimation of unnormalized statistical models? with applications to natural image statistics. Journal of Machine Learning Research. 2012. V. 13. P. 307–361.
Matsuda T., Uehara M., Hyvarinen A. Information criteria for non-normalized models. Journal of Machine Learning Research. 2021. V. 22. P. 1–33.
Vapnik V.N. Statistical Learning Theory. Wiley, 1998. 768 p.
Witten I.H., Eibe F. Data Mining: Practical machine learning tools and tehniques. Morgan Kaufmann, 2005.
Bishop C.M. Pattern Recognition and Machine Learning. Springer, Series: Information Theory and Statistics, 2006.
Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. Springer Series in Statistics, Berlin, 2009. 698 p.
Воронцов К.В. Математические методы обучения по прецендентам. Курс лекций МФТИ. 2013.
Попков Ю.С., Попков А.Ю., Дубнов Ю.А. Рандомизированное машинное обучение при ограниченных объемах данных. УРРС, 2018.
Bruckstein A.M., Donoho D.L., Elad M. From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM review. 2009. V. 51 (1). P. 34–81.
Jolliffe I. Principal component analysis. New York: Springer. 2011. https://doi.org/10.1007/b98835
Поляк Б.Т., Хлебников М.В. Метод главных компонент: робастные версии. Автоматика и телемеханика. 2017. V. 3. P. 130–148.
Bingham E., Mannila H. Random projection in dimensionality reduction: applications to image and text data. Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining. 2001. P. 245–250.
Vempala S.S. The random projection method. American Mathematical Soc. 2005. V. 65.
Popkov Y.S., Dubnov Y.A., Popkov A.Y. Entropy Dimension Reduction Method for Randomized Machine Learning Problems. Automation and Remote Control. 2018. V. 79(11). P. 2038–2051. https://doi.org/10.1134/S0005117918110085
Kullback S., Leibler R.A. On information and sufficiency. The annals of mathematical statistics. 1951. V. 22(1). P. 79–86.
Попков Ю.С., Попков А.Ю. Кросс-энтропийная оптимальная редукция размерности матрицы данных с ограничением информационной емкости. Доклады академии наук. 2019. V. 488. P. 21–23. https://doi.org/10.31857/S0869-5652488121-23
Magnus J.R., Neudecker H. Matrix differential calculus with applications in statistics and econometrics. Wiley. 1988.
Попков Ю.С. Оценки максимальной энтропии непрерывных функций и их асимптотическая эффективность. Доклады Академии наук в печати.
Иоффе А.Д.,Тихомиров В.М. Теория экстремальных задач. М.: Наука. 1974.
Popkov Yu.S. Macrosystems theory and its applications (Lecture notes in control and information sciences) 203. Springer. 1995.
Goldberger A.S. A Course in Econometrics. Harvard University Press, 1991. 437 p.
Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. М., Юнити, 1998.
Лагутин М.Б. Наглядная математическая статистика. М., БИНОМ, Лаборатория знаний, 2013.
Rousses G. A Course of the Mathematical Statistics. Academic Press Inc. 2015. 600 p.
Golan A., Judge G.G., Miller D. Maximum Entropy Econometrics: Robust Estimation with Limited Data. John Wiley and Sons Ltd., Chichester, UK, 1996.
Мандель И.Д. Кластерный анализ. М., Финансы и Статистика, 1988.
Загоруйко Н.Г. Когнитивный анализ данных. Академическое издательство “ГЕО”, 2012. 203 с.
Загоруйко Н.Г., Барахнин В.Б., Борисова И.А., Ткачев Д.А. Кластеризация текстовых документов из электронной базы публикаций алгоритмом FRiS-Tax. Вычислительные технологии. 2013. Т. 6. № 18. С. 62–74.
Jain A., Murty M., Flynn P. Data clastering: a review. ACM Computing surveys. 1990. V. 31. № 3. P. 264–323.
Воронцов К.В. Лекции по алгоритмам кластеризации имногомерному шкалированию. http: // www.ccas.ru/voron/download/Clastering.pdf
Lescovec J., Rajaraman A., Ullman J. Mining of Massive Datasets. Cambridge University Press, 2014. 511 p.
Deerwester S., Dumias S.T., Furnas G.W., Landauer T.K., Harshman R. Indexing by Latent Semantic Analysis. Journal of the American Society for Information Science, 1999. V. 41. P. 391–407.
Zamir O.E. Clastering Web Documents: A Phrase-Based Methods for Grouping Search Engine Results. Uni. of Washington, USA, 1999. P. 65–117.
Cao G., Song D., Bruza P. Suffix-Tree Clastering on Post-retrieval Documents Information. The Uni. of Queensland, 2003.
Jain A., Dubs R. Clastering Methods and Algorithms. Prentice-Hall Inc. 1988.
Pal N.R., Biswas J. Claster validation using graph theoretic consept. Pattern Recognition. 1997. V. 30(6). P. 847–857.
Halkidi M., Batistakis Y., Vazirgiannis M. On clastering validation techniques. Journal of Intelligent Information Systems. 2001. V. 17(2-3). P. 107–145.
Han J., Kamber M., Pei J. Data Mining Consept and Techniques. Third Edition, Morgan Kaufmann Publishers, 2012, 703 p.
Popkov Yu.S. Macrosystem theory and application. Springer, LNIS, 1995.
Aggarval A. Neural Networks and Deap Learning. Springer International Publishing AG, part os Springer Nature, 2018.
Popkov Yu.S. New class of multiplicative algorithms for solving of entropy-linear programs. European Journal of Operation Research. 2006. № 174. P. 1368–1379.
Polyak B.T. Introduction to Optimization, Optimization Software, 1987.
Johnson W.B., Lindenstrauss J. Extensions of Lipshitz mapping into Hilbert Space. Modern Analysis and Probability. 1984. V. 26. P. 189–206.
Achlioptas D. Database-friendly random projections. Amer. Math. Soc., 2001, PODS’01. P. 274–281.
Malout R. A comparison of algorithms for maximum entropy parameters estimation. Proc. of the 6th conference on Natural Language learning, 2002. V. 20. P. 1–7.
Borwein J., Choksi R., Marechal P. Probability Distribution of Assets Inferred from Option Prices via Principle Maximum Entropy. SIAM Journal of Optimization, 2003. V. 14. № 2. P. 464–478.
Golan A. Information andentropy econometrics – a review and synthesis. Foundations and trends in econometrics. 2008. V. 2(1-2). P. 1–145.
Csiszar I., Matus F. On minimization of entropy functionals under moment constraints. IEEE International Symposium on Information Theory, 2008.
Loubes J-M., Rochet Approximate maximum entropy on the mean for instrumental variable regression. Statistics and Probability Letters, 2012. V. 82. Issue 5. P. 972–978.
Borwein J.M., Lewis A.S. Partially-Finite Programming in ${{L}_{1}}$ and Existance of Maximum Entropy Estimates. SIAM Journal of Optimisation, 1993. V. 3. № 2. P. 248–267.
Burg J.P. The relationship between maximum entropy spectra and maximum likelyhood spectra. Geophysics. 1972. V. 37. P. 375–376.
Christakos G. A Bayesian/maximum entropy viewto the spatial estimation problem. Mathematical Geology, 1990. V. 22. P. 763–777.
Singh V.P., Guo H. Parameter estimation for 3-parameter generalized Pareto distribution by the principle maximum entropy. Hydrological Sciences Journal, 1994. P. 165–181.
Popkov Yu.S., Dubnov Yu.A., Popkov A.Yu. Randomized machine learning: Statement, solution, applications // IEEE 8th International Conference on Intelligent Systems (IS) (2016). https://doi.org/10.1109/IS.2016.7737456.
Kolmogorov A.N., Fomin S.V. Elemets of the Theory of Functions and Functional Analysis. Dover Publication, 1999.
Krasnosel’skii M.A., Zabreiko P.P. Geometrical Methods of Nonlinear Analysis. A Series of Comprehensive Studies in Mathematics, 263, Springer-Verlag, 1984, Berlin – Heldenberg – NY, 490 p.
Riordan B., Verbula D., McGruire A.D. Shrinking ponds in subarctic Alaska based on 1950-2002 remotely sensed images. Journal of Geophysic Researches. 2006. V. 111, G04002.
Kirpotin S., Polishchuk Y., Bruksina N. Abrupt changes of thermokarst lakes in Western Siberia: impacts of climatic warming on permafrost melting. International Journal of Environmental Studies. 2009. V. 66. № 4. P. 423–431.
Электронный ресурс: https://cloud.uriit.ru/index.php/s/0DOrxL9RmGqXsV0.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления