Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 506, № 1, стр. 16-19
БИНАРНЫЕ ПРОСТРАНСТВА ОРЛИЧА
1 Самарский национальный исследовательский университет им. академика С.П. Королёва
Самара, Россия
* E-mail: astash56@mail.ru
Поступила в редакцию 13.05.2022
После доработки 02.08.2022
Принята к публикации 10.08.2022
- EDN: VAPORZ
- DOI: 10.31857/S2686954322050034
Аннотация
Подпространство H перестановочно-инвариантного пространства X сильно вложено в X, если на H сходимость в X-норме и по мере эквивалентны. Получены необходимые и достаточные условия на функцию Орлича M, при которых единичный шар любого подпространства, сильно вложенного в пространство Орлича ${{L}_{M}}$, имеет равностепенно непрерывные нормы в ${{L}_{M}}$.
§ 1. Банахово пространство E измеримых на [0, 1] функций называется перестановочно-инвариантным (кратко r.i.), или симметричным, если 1) из того, что x измерима, ${\text{|}}x(t){\text{|}} \leqslant {\text{|}}y(t){\text{|}}$ для всех $t \in [0,1]$ и $y \in E$, следует $x \in E$ и ${\text{||}}x{\text{|}}{{{\text{|}}}_{E}} \leqslant {\text{||}}y{\text{|}}{{{\text{|}}}_{E}}$; 2) из равноизмеримости функций x и y (это означает, что
Самый известный пример r.i. пространств – пространства ${{L}^{p}}$, $1 \leqslant p \leqslant \infty $. Их естественным обобщением являются пространства Орлича [4, 5]. Пусть M – непрерывная выпуклая возрастающая функция на $[0,\infty )$, $M(0) = 0$. Пространство Орлича ${{L}_{M}}$ состоит из всех измеримых на [0, 1] функций, для которых конечна норма Люксембурга
Если $M(u) = {{u}^{p}}$, то ${{L}_{M}} = {{L}^{p}}$ изометрически. Пространство LM сепарабельно тогда и только тогда, когда M удовлетворяет ${{\Delta }_{2}}$-условию в бесконечности ($M \in \Delta _{2}^{\infty }$), т.е. $M(2u) \leqslant CM(u)$ для некоторого C > 0 и всех достаточно больших u.
Для каждой функции Орлича M определим следующие непустые компактные подмножества пространства $C[0,1]$:
Множество $C_{M}^{\infty }$ определяет структуру подпространств, порожденных последовательностями попарно дизъюнктных функций в пространстве LM [6] (измеримые функции $x$ и $y$ дизъюнктны, если ${\text{mes}}(\{ t{\kern 1pt} :\;x(t) \ne 0\} \cap \{ t{\kern 1pt} :\;y(t) \ne 0\} )$ = 0). Легко проверить, что $1 \leqslant \alpha _{M}^{\infty } \leqslant \beta _{M}^{\infty } \leqslant \infty $.
Аналогично, если $\psi $ – функция Орлича, то пространство Орлича последовательностей ${{\ell }_{\psi }}$ состоит из всех последовательностей $({{a}_{k}})_{{k = 1}}^{\infty }$, для которых
Если $1 \leqslant p < \infty $, $\varphi $ – непрерывная возрастающая вогнутая на [0, 1] функция, $\varphi (0) = 0$, то пространство Лоренца ${{\Lambda }_{p}}(\varphi )$ состоит из всех измеримых на [0, 1] функций, для которых ${\text{||}}x{\text{|}}{{{\text{|}}}_{{{{\Lambda }_{p}}(\varphi )}}}$ := := ${{\left( {\int\limits_0^1 {x{\kern 1pt} {\text{*}}{{{(t)}}^{p}}{\kern 1pt} d\varphi (t)} } \right)}^{{1/p}}}$ < ∞.
Говорят, что (замкнутое линейное) подпространство H r.i. пространства X сильно вложено в X, если сходимость в X-норме и по мере на H эквивалентны. В частности, в силу неравенства Хинчина [7, глава V, теорема 8.4] функции Радемахера ${{r}_{k}}(t) = {\text{sign}}(\sin {{2}^{k}}\pi t)$, $k \in N$, $t \in [0,1]$, порождают сильно вложенное подпространство в Lp для каждого $1 \leqslant p < \infty .$
Множество $K \subset X$ имеет равностепенно непрерывные нормы в r.i. пространстве X, если $\mathop {\lim }\nolimits_{\delta \to 0} \mathop {\sup }\nolimits_{m(E) < \delta } \mathop {\sup }\nolimits_{x \in K} {\text{||}}x{{\chi }_{E}}{\text{|}}{{{\text{|}}}_{X}}$ = 0. Нетрудно показать, что подпространство H сильно вложено в X, если его единичный шар ${{B}_{H}}: = \{ x \in X{\kern 1pt} :\;{\text{||}}x{\text{|}}{{{\text{|}}}_{X}} \leqslant 1\} $ имеет равностепенно непрерывные нормы в X.
Введенные понятия тесно связаны со свойствами величины
Ясно, что всегда $0 \leqslant {{\eta }_{X}}(K) \leqslant 1$. Если H – подпространство r.i. пространства X и ${{\eta }_{X}}(H) < 1$, то H сильно вложено в X. Кроме того, ${{\eta }_{X}}(H) = 0$ тогда и только тогда, когда единичный шар ${{B}_{H}}$ имеет равностепенно непрерывные нормы в X.
Вслед за [11] назовем r.i. пространство X бинарным, если ${{\eta }_{X}}(H)$ принимает на его подпространствах H только два значения: 0 и 1. Как легко видеть, r.i. пространство $X$ бинарно, если единичный шар ${{B}_{H}}$ всякого сильно вложенного в X подпространства $H$ имеет равностепенно непрерывные нормы в X.
Согласно известной теореме Х.П. Розенталя [12, теорема 13] пространство ${{L}^{p}}$ бинарно, если $1 \leqslant p < 2$ (нетрудно показать, что последнее условие необходимо). В [11] (см. также [10]) этот результат (при таком же условии на p) был распространен на пространства Лоренца ${{\Lambda }_{p}}(\varphi )$.
Будучи тесно связанной со свойствами подпространств, величина ${{\eta }_{X}}(K)$ является важной геометрической характеристикой r.i. пространства X. Как выяснено в настоящей работе, вопрос о бинарности r.i. пространства X определяется структурой подпространств X, порождаемых последовательностями попарно дизъюнктных функций в нем. Если в пространствах Лоренца ${{\Lambda }_{p}}(\varphi )$ она достаточно проста (всякая такая нормированная последовательность содержит подпоследовательность, эквивалентную стандартному базису в lp [13]), то в пространствах Орлича она гораздо сложнее. В работе получены необходимые и достаточные условия бинарности пространств Орлича.
§ 2. Всюду далее функция Орлича M удовлетворяет условию: $1 < \alpha _{M}^{\infty } \leqslant \beta _{M}^{\infty } < 2$.
В доказательстве следующего ключевого утверждения используются конструкции из работы [14].
Предложение 1. Если в пространстве Орлича ${{L}_{M}}$ существует сильно вложенное подпространство, единичный шар которого имеет не равностепенно непрерывные нормы в ${{L}_{M}}$, то для некоторой $\psi \in C_{M}^{\infty }$ выполнено: $1{\text{/}}{{\psi }^{{ - 1}}} \in {{L}_{M}}$.
Применяя предложение 1 вместе с результатами работ [6] и [15], получаем
Теорема 1. Предположим, что 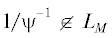 для всякой функции $\psi \in C_{M}^{\infty }$. Тогда, если H – подпространство ${{L}_{M}}$, то следующие условия эквивалентны:
для всякой функции $\psi \in C_{M}^{\infty }$. Тогда, если H – подпространство ${{L}_{M}}$, то следующие условия эквивалентны:
(i) H не содержит бесконечномерных подпространств, изоморфных подпространствам, порожденным в ${{L}_{M}}$ попарно дизъюнктными функциями;
(ii) H сильно вложено в ${{L}_{M}}$;
(iii) единичный шар ${{B}_{H}}$ имеет равностепенно непрерывные нормы в ${{L}_{M}}$.
Следующее утверждение содержит легко проверяемые достаточные условия на функцию M, при которых 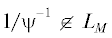 для каждой $\psi \in C_{M}^{\infty }$.
для каждой $\psi \in C_{M}^{\infty }$.
Предложение 2. Пусть M – функция Орлича, $1 < \alpha _{M}^{\infty } \leqslant \beta _{M}^{\infty } < 2$. Предположим, что выполнено хотя бы одно из следующих условий:
(a) $M(uv) \leqslant {{C}_{1}}M(u)M(v)$ для некоторого ${{C}_{1}} > 0$ и всех $u,v \geqslant 1$;
(b) 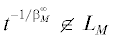 и для некоторого ${{C}_{2}} > 0$
и для некоторого ${{C}_{2}} > 0$
Тогда 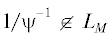 для каждой функции $\psi \in C_{M}^{\infty }$.
для каждой функции $\psi \in C_{M}^{\infty }$.
Как следствие, получаем вариант упоминавшейся теоремы Х.П. Розенталя о структуре подпространств ${{L}^{p}}$-пространств для пространств Орлича: если функция Орлича M удовлетворяет хотя бы одному из условий (a) или (b) предложения 2 и H – подпространство пространства Орлича LM, то условия (i), (ii) и (iii) эквивалентны. Таким образом (см. § 1), в этом случае пространство LM бинарно.
Напомним, что функция Орлича M, $M \in \Delta _{2}^{\infty }$, называется правильно меняющейся на бесконечности порядка p, если ${{\lim }_{{t \to \infty }}}M(tu){\text{/}}M(t)$ = up. Примером является функция M(u) = = ${{u}^{p}}{{(\ln u)}^{{{{q}_{1}}}}}{{(\ln \,\ln \,u)}^{{{{q}_{2}}}}} \ldots {{(\ln \ldots \ln \,u)}^{{{{q}_{n}}}}},$ где $p \in (1,\infty )$, а вещественные числа ${{q}_{1}}, \ldots ,{{q}_{n}}$ произвольны. Если M – правильно меняющаяся на бесконечности функция порядка p, то $C_{M}^{\infty } = \{ {{t}^{p}}\} $. Поэтому в силу предложения 2 построенное по такой функции пространство Орлича LM бинарно.
В следующей теореме приведено необходимое условие бинарности пространства Орлича, которое зачастую также и достаточно.
Теорема 2. Если пространство Орлича ${{L}_{M}}$ бинарно, то 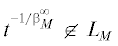 . Если дополнительно выполнено (1), то верно также обратное: из того, что
. Если дополнительно выполнено (1), то верно также обратное: из того, что 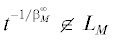 , вытекает бинарность LM.
, вытекает бинарность LM.
Для подпространств, изоморфных пространствам Орлича последовательностей, получен более точный результат.
Теорема 3. Для того, чтобы единичный шар ${{B}_{H}}$ произвольного сильно вложенного подпространства H пространства Орлича LM, изоморфного некоторому пространству Орлича последовательностей, имел в LM равностепенно непрерывные нормы, необходимо и достаточно, чтобы 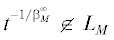 .
.
Список литературы
Lindenstrauss J., Tzafriri L. Classical Banach spaces II. Function spaces. V. 97. B.: Springer-Verlag, 1979. 246 p.
Крейн С.Г., Петунин Ю.И., Семенов Е.М. Интерполяция линейных операторов. М.: Наука, 1978. 400 с.
Bennett C., Sharpley R. Interpolation of operators. London: Academic Press, 1988. 469 p.
Красносельский М.А., Рутицкий Я.Б. Выпуклые функции и пространства Орлича. М.: Физматгиз, 1958. 271 с.
Rao M.M., Ren Z.D. Theory of Orlicz spaces, Monographs and Textbooks in Pure and Applied Mathematics. V. 146. N.Y.: Marcel Dekker Inc., 1991. 445 p.
Lindenstrauss J., Tzafriri L. On Orlicz sequence spaces. III // Israel J. Math. 1973. V. 14. P. 368–389.
Зигмунд А. Тригонометрические ряды. Т. I. М.: Мир, 1965. 615 с. [перевод с английского Zygmund A. Trigonometric series. V.I. Cambridge Univ. Press, Cambridge, UK, 1959.]
Токарев Е.В. О подпространствах некоторых симметричных пространств // В сб. “Теория функций, функциональный анализ и их приложения”, вып. 24, Харьков, 1975, С. 156–161.
Kadec M.I., Pełczyński A. Bases, lacunary sequences and complemented subspaces in the spaces ${{L}_{p}}$ // Studia Math. 1962. V. 21. P. 161–176.
Новиков С.Я., Семенов Е.М., Токарев Е.В. Структура подпространств пространств ${{\Lambda }_{p}}$ // Докл. АН СССР. 1979. Т. 243. № 3. С. 252–254.
Новиков С.Я., Семенов Е.М., Токарев Е.В. О структуре подпространств пространств ${{\Lambda }_{p}}(\mu )$ // В сб. “Теория функций, функциональный анализ и их приложения”, вып. 42, Харьков, 1984. С. 91–97.
Rosenthal H.P. On subspaces of ${{L}^{p}}$ // Annals of Math. 1973. V. 97. P. 344–373.
Figiel T., Johnson W. B., Tzafriri L. On Banach lattices and spaces having local unconditional structure with applications to Lorentz function spaces // J. Approx. Theory. 1975. V. 13. P. 395–412.
Astashkin S.V. $\Lambda (p)$-spaces // J. Funct. Anal. 2014. V. 266. P. 5174–5198.
Astashkin S.V. On symmetric spaces containing isomorphic copies of Orlicz sequence spaces // Comment. Math. 2016. V. 56. № 1. P. 29–44.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


