Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 506, № 1, стр. 30-36

О СТАБИЛИЗАЦИИ ЯВНОЙ СХЕМЫ РЕШЕНИЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА

Академик РАН Б. Н. Четверушкин¹, О. Г. Ольховская^1, *, В. А. Гасилов¹

¹ Институт прикладной математики им. М.В. Келдыша Российской академии наук
Москва, Россия

Поступила в редакцию 10.06.2022
После доработки 12.07.2022
Принята к публикации 25.07.2022

EDN: PXXSHA
DOI: 10.31857/S268695432205006X

Аннотация

Разработан метод численного решения нелинейного уравнения, описывающего диффузионный перенос энергии излучения. Метод основан на введении в параболическое уравнение второй производной по времени с малым параметром и явной разностной схеме. Явная аппроксимация исходного уравнения позволяет реализовать на ее основе алгоритм, эффективно адаптированный к архитектуре высокопроизводительных вычислительных систем. Новая схема обеспечивает разрешение нелинейности со вторым порядком по времени с приемлемым временным шагом. Предложен эвристический алгоритм выбора параметров трехслойной разностной схемы. Перспективной областью приложений метода могут быть задачи астрофизики, например, такие, как расчет выхода сильноизлучающей ударной волны к поверхности звезды в стадии ее эволюции, известной как “вспышка сверхновой”.

Ключевые слова: лучистый теплообмен, модель диффузии излучения, нелинейное параболическое уравнение, явная разностная схема, высокопроизводительные вычисления

1. ВВЕДЕНИЕ

Численное моделирование является одним из важнейших методов теоретической астрофизики, а моделирование процессов переноса излучения, механизмов излучения электромагнитных волн и его взаимодействия с веществом образует самостоятельное направление в круге вычислительных астрофизических задач. Результаты расчетов процессов взаимодействия излучения с веществом при сопоставлении с информацией, поступающей от звезд и галактик в виде электромагнитного излучения, позволяют определить температуру и химический состав звездных атмосфер, размеры и массы звезд. Тем самым создается основа для предсказаний эволюции астрофизических объектов и вселенной в целом.

В астрофизических исследованиях находят применение различные модели переноса энергии излучением. Задача расчета поля излучения, распространяющегося в космосе, весьма сложна. В общем виде она решается в многогрупповой по спектру модели радиационной плазмодинамики и включает учет релятивистских факторов – охлаждения электронной компоненты плазмы за счет обратного комптон-эффекта, влияния эффекта Допплера, аберрации и т.д. [1, 2]. В тех случаях, когда можно использовать приближение оптически толстой среды, лучистый поток энергии можно рассчитывать по упрощенным моделям – диффузии излучения либо лучистой теплопроводности. В таких моделях можно выделить задачу для параболического уравнения с коэффициентом, нелинейно зависящим от температуры (энергии) излучения. Часто необходимо также учитывать нелинейные граничные условия, например, условия на поверхности излучающего тела (задачи с внешней нелинейностью).

Для постановок задач радиационной гидродинамики, возникающих при анализе взрывов сверхновых, характерна существенная пространственно-временная разномасштабность. Пространственные сетки для аппроксимации таких задач в трехмерной постановке могут состоять из десятков миллиардов узлов. Для решения этих задач за приемлемое время необходимо использовать вычислительные мощности современных суперкомпьютеров с большим числом независимых вычислителей (процессоров, ядер, тредов).

Моделирование на вычислительных системах высокой и сверхвысокой производительности требует разработки эффективных и надежных численных методов и алгоритмов, масштабируемых на современные и перспективные компьютерные архитектуры. Неявные схемы для уравнений диффузионного типа обладают абсолютной устойчивостью и позволяют вести расчет на подробных пространственных сетках с приемлемым шагом по времени. Однако для нахождения решения на их основе необходимо прибегать к тем или иным итерационным процессам, которые связаны с логическими процедурами и плохо адаптируются на архитектуру систем с экстрамассивным параллелизмом. Эффективность параллельной обработки падает при одновременном использовании большого числа вычислителей. Особенно чувствительны оказываются перспективные гетерогенные системы, использующие в качестве ускорителей графические платы (GP GPU). В нелинейных задачах итерационные процедуры усложняются, что приводит к резкому увеличению объема вычислений. Использование локально-адаптивных сеток, в частности сеток древовидной структуры с дроблением/слиянием ячеек позволяет аккуратно воспроизводить тонкие пространственные структуры. Однако при этом ухудшается обусловленность системы линейных уравнений на верхнем слое, тем самым также увеличивая число итераций. Вычислительные затраты такого рода можно сократить, заметно уменьшив шаг по времени. Тем самым теряется преимущество неявных схем – возможность вести расчеты с “гидродинамическим” шагом по времени.

Явные схемы идеальны для параллельной обработки. Однако для их устойчивости требуется жесткое ограничение на шаг по времени τ: τ ≤ ≤ h²/2κ (h – характерный размер пространственной сетки, κ – эффективный коэффициент диффузии). Как правило, величина κ резко возрастает с ростом температуры, что еще больше ограничивает τ.

Таким образом, численное решение нелинейного параболического уравнения на подробных пространственных сетках, для которого собственно и нужны высокопроизводительные системы с экстрамассивным параллелизмом, реально затруднено. Ранее нами была предложена гиперболическая модель для лучистой теплопроводности [3], позволяющая применять для расчетов на многопроцессорных системах явную схему с более мягким условием устойчивости. Подобный подход представляется эффективным и для других задач, описываемых нелинейным параболическим уравнением, в частности для моделирования переноса излучения.

2. НЕЛИНЕЙНОЕ ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ С РЕГУЛЯРИЗАЦИЕЙ

Рассмотрим квазилинейное параболическое уравнение

(1)

$C(t,u)\frac{{\partial u}}{{\partial t}} = {\text{div}}\left( {\kappa (t,u) \cdot {\text{grad}}\,u} \right) + Q(t,u)$

Например, для лучистой теплопроводности $\kappa = \frac{{16\sigma \,{{T}^{3}}l\left( {T,\,\rho } \right)}}{3}$ (T – температура среды, ρ – плотность, σ – постоянная Стефана-Больцмана, l – длина свободного пробега фотона, осредненная по Росселанду), при этом для многих сред $l\,\sim \,{{T}^{\gamma }}$. Для электронной теплопроводности в горячей плазме $\kappa \sim {{T}^{{5/2}}}$. При расчетах необходимо учитывать особенности поверхностного излучения для твердых тел и объемного излучения для излучающих и поглощающих газов. Граничное условие на излучающей поверхности (закон Стефана-Больцмана) есть $\frac{{\partial T}}{{\partial n}}\, = \varepsilon \cdot \sigma \cdot {{T}^{4}}$, где 0 < ε ≤ 1 – степень черноты (0 – излучение отсутствует, 1 – излучение абсолютно черного тела).

По аналогии с гиперболической моделью теплопроводности [3] вместо уравнения (1) предлагается рассматривать уравнение (2) с малым параметром ω:

(2)

$C\frac{{\partial u}}{{\partial t}} + \omega \frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} = {\text{div}}(\kappa \cdot {\text{grad}}\,u) + Q$

Трехслойная разностная схема уравнения (2) для сеточной функции {U_n} c постоянным шагом по времени Δt строится следующим образом:

(3)

$\begin{gathered} \frac{{\partial U}}{{\partial t}} \to \frac{{\mathop U\nolimits_n^{m + 1} - \mathop U\nolimits_n^{m - 1} }}{{2\tau }}, \\ \omega \frac{{{{\partial }^{2}}U}}{{\partial {{t}^{2}}}} \to \omega \frac{{\mathop U\nolimits_n^{m + 1} - 2\mathop U\nolimits_n^m + U_{n}^{{m - 1}}}}{{{{\tau }^{2}}}}, \\ \nabla \left( {\kappa \nabla U} \right) \to \left\langle {\nabla \left( {\kappa \nabla U} \right)} \right\rangle _{n}^{m},\quad Q \to Q(\mathop U\nolimits_n^m ) \\ \end{gathered} $

Здесь n – обобщенный индекс пространственной ячейки, m – номер шага по времени. Пространственный член, включающий нелинейный по температуре коэффициент, аппроксимируется на на m-м слое по времени с использованием известного значения U^m. Итерации не нужны, в этом преимущество предложенной схемы. Схема (3) обеспечивает второй порядок точности по времени.

Гиперболизированное уравнение может использоваться также и в лагранжевых схемах.

Рассмотрим уравнение в форме:

(4)

$C\frac{{\partial u}}{{\partial t}} + \omega \frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} + {{w}_{i}}\frac{{\partial u}}{{\partial {{x}_{i}}}} = {\text{div}}\,\kappa grad\,U$

В лагранжевых координатах реализуется уравнение (4) без второй производной по времени

(5)

$C\frac{{\partial u}}{{\partial t}} + {{w}_{i}}\frac{{\partial u}}{{\partial {{x}_{i}}}} = {\text{div}}\,\kappa grad\,u$

Как вписать в лагранжеву схему член $\omega \frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}$? Его исходная разностная аппроксимация в эйлеровых координатах приведена в формуле (3):

$\omega \,\frac{{\mathop U\nolimits_n^{m + 1} - \mathop {2U}\nolimits_n^m + \mathop U\nolimits_n^{m - 1} }}{{{{\tau }^{2}}\,}}$

В лагранжевых координатах аппроксимация будет иметь вид:

(6)

$\omega \frac{{\mathop U\nolimits_{n{\kern 1pt} '}^{m + 1} - \mathop {2U}\nolimits_n^m + \mathop U\nolimits_{n{\kern 1pt} '{\kern 1pt} '}^{m - 1} }}{{{{\tau }^{2}}}}$

Здесь точки n' и n'' смещены за счет газодинамического переноса.

Определим с учетом этого переноса величины U_n' и U_n''.

(7)

$\begin{gathered} \mathop U\nolimits_{n'}^{m + 1} = \mathop U\nolimits_n^{m + 1} + {{w}_{i}} \cdot \tau \cdot \frac{{\partial {{U}^{m}}}}{{\partial {{x}_{i}}}} + \frac{{\mathop {\mathbf{w}}\nolimits^2 \cdot \mathop \tau \nolimits^2 }}{2} \cdot \Delta \mathop U\nolimits^m \\ \mathop U\nolimits_{n'}^{m - 1} = \mathop U\nolimits_n^{m - 1} - {{w}_{i}} \cdot \tau \cdot \frac{{\partial {{U}^{m}}}}{{\partial {{x}_{i}}}} + \frac{{\mathop {\mathbf{w}}\nolimits^2 \cdot \mathop \tau \nolimits^2 }}{2} \cdot \Delta \mathop U\nolimits^m \\ \end{gathered} $

С учетом (7) выражение (6) для лагранжевой аппроксимации второй производной по времени можно представить в виде:

(8)

$\omega \cdot \frac{{\mathop U\nolimits_n^{m + 1} - \mathop {2U}\nolimits_n^m + \mathop U\nolimits_n^{m - 1} }}{{{{\tau }^{2}}}} + \omega \cdot {{{\mathbf{w}}}^{2}}\Delta {{U}^{m}}$

Таким образом, лагранжева аппроксимация (6) отличается от исходной эйлеровой аппроксимации (3) дополнительным членом $\omega \cdot {{{\mathbf{w}}}^{2}}\Delta {{U}^{m}}$, который надо вычесть из члена $\nabla \,(\kappa \,\nabla \,U)$ в уравнении (4):

(9)

$\nabla \,(\kappa \,\nabla \,U) - \omega \cdot {{{\mathbf{w}}}^{2}}\mathop {\Delta U}\nolimits^m $

Ввиду малости ω ($\omega \leqslant {h \mathord{\left/ {\vphantom {h {\left| {\mathop V\nolimits_{хар} } \right|}}} \right. \kern-0em} {\left| {\mathop V\nolimits_{хар} } \right|}}$, V_хар – характерная скорость процесса, см. [4]) и большого коэффициента теплопроводности κ в выражении (9) последним членом $\omega \cdot {{{\mathbf{w}}}^{2}}\Delta {{U}^{m}}$, имеющим ту же функциональную структуру, что и член $\nabla \,(\kappa \,\nabla \,U)$, можно пренебречь.

Поэтому для уравнения (4) можно использовать лагранжеву аппроксимацию (5) с добавлением регуляризатора в той же форме, как и в схеме (3)

$\omega \frac{{\mathop U\nolimits_n^{m + 1} - \mathop {2U}\nolimits_n^m + \mathop U\nolimits_n^{m - 1} }}{{{{\tau }^{2}}}},$

где $\mathop U\nolimits_n^{m + 1} $ и $\mathop U\nolimits_n^{m - 1} $ заменяют сдвинутые за счет газодинамического движения значения $\mathop U\nolimits_{n{\kern 1pt} '}^{m + 1} $ и $\mathop U\nolimits_{n{\kern 1pt} '{\kern 1pt} '}^{m - 1} $.

Такой подход может быть полезен для астрофизических расчетов, где вещество движется с огромными скоростями и решение уравнений переноса излучения осуществляется в лабораторной системе отсчета [5].

3. ВЫБОР ПАРАМЕТРОВ ТРЕХСЛОЙНОЙ РАЗНОСТНОЙ СХЕМЫ

В ряде работ [4, 6–9], выполненных в ИПМ РАН, был проведен анализ гиперболического уравнения теплопроводности и трехслойной разностной схемы для его численного решения. Оценки, полученные из математической теории, включая разницу между решениями уравнения (1) и уравнения (2), ограничение величины малого параметра ω и ограничение шага по времени для явной схемы (3) , относятся в основном к линейному уравнению и одномерной по пространству разностной схеме. В работе [10] представлены результаты тестовых расчетов задачи о мгновенном источнике тепла в линейной постановке, на которой в полной мере проявляется отличие гиперболизованной теплопроводности от классической. Вычислительные эксперименты [3, 11] показали применимость этих оценок для нелинейного уравнения со степенной зависимостью коэффициента теплопроводности от температуры и для разностных схем на трехмерных сетках регулярной и нерегулярной структуры. На основании этих исследований предложен эвристический алгоритм выбора параметров разностной схемы.

3.1. Диссипация и дисперсия сеточного решения

Рассмотрим одномерное линейное гиперболическое уравнение теплопроводности:

(10)

$\frac{{\partial U}}{{\partial t}} + \omega \frac{{{{\partial }^{2}}U}}{{\partial {{t}^{2}}}} = \frac{\partial }{{\partial x}}\left( {\kappa \frac{{\partial U}}{{\partial x}}} \right)$

Здесь κ – коэффициент температуропроводности, ω – малый параметр, имеющий размерность времени и много меньший характерного времени процесса.

Трехслойная потоковая схема, аппроксимирующая уравнение (10) на равномерной пространственной сетке с постоянным шагом по времени:

(11)

$\begin{gathered} \frac{{\mathop U\nolimits_m^{n + 1} - \mathop U\nolimits_m^{n - 1} }}{{2\tau }} + \omega \frac{{\mathop U\nolimits_m^{n + 1} - 2U_{m}^{n} + U_{m}^{{n - 1}}}}{{{{\tau }^{2}}}} = \\ \, = \frac{1}{{{{h}^{2}}}}\left( {{{\kappa }^{ + }}(\mathop U\nolimits_{m + 1}^n - \mathop U\nolimits_m^n ) - {{\kappa }^{ - }}(\mathop U\nolimits_m^n - \mathop U\nolimits_{m - 1}^n )} \right) \\ \end{gathered} $

Здесь τ – шаг интегрирования по времени, n – номер шага по времени, h – шаг пространственной сетки, m – номер узла пространственной сетки, κ⁺ = κ_m_{+ 1/2} относится к точке х_m _{+ 1/2}= h · m + + h/2, κ^– = κ_m_{– 1/2} – к точке х_m _{– 1/2} = h · m – h/2.

Подставляя в схему (11) решение в виде

$U_{m}^{n} = {{U}_{0}}\exp \left( {i(\nu \tau n - khm)} \right),$

где i² = –1, построим дисперсионное соотношение:

(12)

$\begin{gathered} \frac{1}{\tau }i\sin (\nu \tau ) - \frac{{4\omega }}{{{{\tau }^{2}}}}{{\sin }^{2}}\left( {\frac{{\nu \tau }}{2}} \right) = \\ \, = - \frac{1}{{{{h}^{2}}}}2({{\kappa }^{ + }} + {{\kappa }^{ - }}){{\sin }^{2}}\left( {\frac{{kh}}{2}} \right) - \frac{1}{{{{h}^{2}}}}({{\kappa }^{ + }} - {{\kappa }^{ - }})i\sin (kh) \\ \end{gathered} $

Анализ дисперсионного уравнения (12) показывает, что дисперсия в схеме присутствует при всех ω > 0, однако при $\omega < \frac{{2h}}{{({{\kappa }^{ + }} + {{\kappa }^{ - }})k}}$ флуктуации затухают. Здесь $\frac{{({{\kappa }^{ + }} + {{\kappa }^{ - }})}}{2}k$ соответствует скорости распространения волны с волновым числом k.

Величину флуктуаций можно оценить как разницу решений параболического и гиперболического уравнений, поскольку для классического параболического уравнения дисперсия отсутствует. Оценка этой разницы δ была выполнена в работе [6].

В интегральной норме:

(13)

${{\left\| {\delta (\bar {x},t)} \right\|}_{{{{L}_{2}}(D \times (0,T))}}} \leqslant \omega {{T}^{2}}{{\left\| {\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}} \right\|}_{{{{L}_{2}}(D \times (0,T))}}}$

Здесь D – расчетная область, Т – полное время решения.

В равномерной норме для одномерного уравнения теплопроводности с постоянными коэффициентами:

(14)

$\begin{gathered} \left| {\delta (\tilde {x},t)} \right| \leqslant M\omega \left( {1 + \frac{2}{{\sqrt \pi }}} \right)\left( {8\sqrt 2 \omega + \frac{{\sqrt[4]{{2{{\pi }^{2}}}}}}{2}T} \right), \\ M = \max \left| {\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}(\xi ,\theta )} \right|\quad 0 \leqslant \theta \leqslant t \\ x - (t - \theta ){\text{/}}\sqrt \omega \leqslant \xi \leqslant x + (t - \theta ){\text{/}}\sqrt \omega \\ \end{gathered} $

Здесь также Т – полное время решения.

Аналогичные оценки для разностных схем были получены в работе [7]. Из этих оценок следует, что, поскольку в разностной задаче вариации по времени связаны с коротковолновыми изменениями по пространству, всегда ограниченными размером ячейки сетки, возмущение, которое вносит малый параметр в численное решение, можно считать регулярным.

3.2. Условие устойчивости и выбор малого параметра ω

Анализ устойчивости трехслойной схемы для линейного уравнения был проведен в статье [5]. В этой работе показано, что при ω = h/V для обеспечения устойчивости трехслойной схемы (3) необходимо выполнение условия

(15)

$\tau \leqslant a{{h}^{{3/2}}};\quad a \sim \frac{1}{{\sqrt {V\kappa } }}.$

Здесь h – шаг пространственной сетки; V – характерная скорость процесса, описываемого уравнением (10), например, скорость света в случае распространения излучения в вакууме или скорость волны в среде; κ – коэффициент диффузии.

В практических задачах характерная скорость распространения тепловой волны часто бывает заранее неизвестна.

В книге [12] предлагается следующая оценка скорости распространения тепла для нелинейной теплопроводности вида ${{C}_{v}}\rho \frac{{\partial T}}{{\partial t}} = {\text{div}}\,(\alpha {{T}^{n}}){\text{grad}}\,T$:

Координата фронта волны ${{x}_{0}} \sim {{\left( {\frac{Q}{{{{C}_{v}}\rho }}} \right)}^{{\frac{n}{{n + 2}}}}}{{(\alpha t)}^{{\frac{1}{{n + 2}}}}}$

Скорость перемещения границы х₀

(16)

${{v}_{0}} \sim \frac{{{{x}_{0}}}}{t} \sim {{\left( {\frac{Q}{{{{C}_{v}}\rho }}} \right)}^{{\frac{n}{{n + 2}}}}}{{(\alpha )}^{{\frac{1}{{n + 2}}}}}{{t}^{{ - \frac{{n + 1}}{{n + 2}}}}}$

Здесь Q [Дж/м²] – количество теплоты, выделяемое источником на границе х = 0.

В задаче о нагреве лазерной мишени, описанной в статье [11], оценка скорости тепловой волны при лучистой теплопроводности была сделана на основании предварительного одномерного расчета.

При нарушении критерия

(17)

$\omega \leqslant h{\text{/}}V$

из-за сеточной дисперсии на фронте температурной волны развиваются незатухающие нефизические осцилляции.

3.3. Алгоритм выбора параметров схемы

Таким образом, предлагается следующий подход к выбору параметров трехслойной разностной схемы (3) для гиперболизированного нелинейного уравнения (2).

1) Построить пространственную разностную сетку, исходя из необходимой точности решения и имеющихся вычислительных мощностей, оценить характерный линейный размер сетки h.

2) Оценить характерную скорость процесса V, исходя из размерностной оценки (16), на основании физических данных или с помощью предварительного одномерного расчета.

3) Задать малый параметр в соответствии с критерием (17): ω = qh/V, 0 < q < 1.

4) Оценить допустимый шаг интегрирования по времени τ из условия устойчивости (15): $\tau \leqslant \sqrt {\frac{\omega }{\kappa }} h$ = $\frac{{{{h}^{{3/2}}}}}{{\sqrt {V\kappa } }}.$

4. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ТРЕХСЛОЙНОЙ РАЗНОСТНОЙ СХЕМЫ

С целью численной проверки алгоритма 3.3 решалось одномерное нелинейное уравнение теплопроводности в форме

(18)

$\frac{{\partial T}}{{\partial t}} + \omega \frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}} = \frac{\partial }{{\partial x}}\left( {{{T}^{\alpha }}\frac{{\partial T}}{{\partial x}}} \right)$

со следующими параметрами: α = 3,0; начальные условия T(t = 0, x) = 10^–4; граничное условие T(x = 0, t) = 0.1; время решения t_max = 100.

В этом случае максимальное значение коэффициента теплопроводности κ_max = 10^–3. Оценка скорости распространения тепловой волны была получена в результате численного решения параболического уравнения теплопроводности по классической схеме, V = 2.75 × 10^–4. Для расчетов использовалась равномерная пространственная сетка из 200 узлов, h = 0.002. Таким образом, максимальное допустимое значение параметра ω: ω_max = h/V = 7.27.

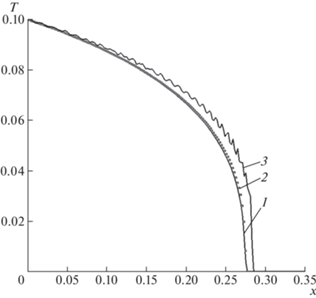
Численное решение уравнения (18) на момент времени t = t_max = 100 представлено на рис. 1.

Рис. 1.

Решение нелинейного уравнения теплопроводности.

Кривая 1 – решение параболического уравнения, ω = 0 в (18). Двухслойная явная схема, расчет с максимальным допустимым шагом по времени τ = h²/(2κ) = 0.002.

Кривая 2 (серые точки) – решение гиперболического уравнения (18) с ω = 1 < ω_max. Трехслойная явная схема. Найденный максимально допустимый шаг по времени τ = 0.038 в 19 раз больше, чем для параболического уравнения. Оценка шага по времени, полученная из линейной теории: $\tau \leqslant \sqrt {\frac{\omega }{\kappa }} h = 0.0632$, немного выше фактически достигнутого значения.

Кривая 3 – решение гиперболического уравнения (18) при нарушении критерия ω ≤ h/V. Трехслойная явная схема, ω =10 > ω_max. Численная дисперсия приводит к нефизическим осцилляциям даже при очень маленьком шаге по времени τ = 0.001 (меньше, чем для параболического уравнения).

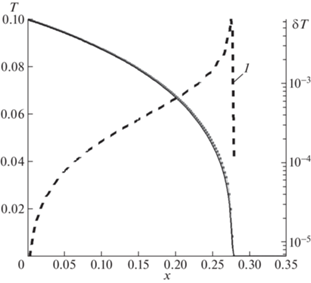
На рис. 2 сплошная кривая и точки соответствуют тем же численным решениям параболического и гиперболического уравнений теплопроводности, а кривая 1 (штриховая) показывает их разность δТ = |Т_пар – Т_гип|. Относительная разница решений в норме L² составила 1.66 × 10^–5.

Рис. 2.

Разность решений параболического и гиперболического уравнений теплопроводности.

Таким образом, показано, что при выборе малого параметра и шага по времени в соответствии с предложенным алгоритмом 3.3 трехслойная разностная схема (3) аппроксимирует нелинейное уравнение (1) и позволяет вести расчет с шагом по времени, существенно большим, чем допускается для явной схемы без регуляризации.

5. ЗАКЛЮЧЕНИЕ

Регуляризация нелинейного параболического уравнения введением второй производной по времени с малым параметром ω является полезным инструментом численного решения таких уравнений с использованием явной по времени разностной схемы. Эти преимущества особенно ярко проявляются по сравнению с параболической моделью, когда использование подробных пространственных сеток поддерживается высокопроизводительными системами с гибридной архитектурой. Одной из перспективных областей приложения разработанной численной методики является моделирование переноса излучения в актуальных задачах астрофизики.

Явная трехслойная схема позволяет точно моделировать быстрые процессы с сильно нелинейным коэффициентом диффузии. Предложен и протестирован эвристический алгоритм выбора параметров схемы, основанный на априорной оценке скорости распространения тепла. Показано, что выполнение критерия ω ≤ h/V обеспечивает как близость к классическому параболическому решению, так и заметную вычислительную эффективность при использовании явных схем.

Явные схемы хорошо вписываются в архитектуру высокопроизводительных вычислительных систем, включая многоуровневый параллелизм с использованием MPI/OpenMP/Cuda для кластеров CPU-GPU. Нами уже накоплен богатый опыт пространственной аппроксимации диффузионных операторов на разного рода неструктурированных пространственных сетках и сетках типа “восьмеричное дерево” с локальной адаптацией. В этих случаях неявная схема приводит к системе линейных алгебраических уравнений с распределенной разреженной матрицей сложной структуры. Итерационная процедура решения такой системы требует дополнительных обменов данными, и ее сходимость не всегда может быть очевидной. Сильная нелинейность, характерная для астрофизических моделей, в свою очередь требует очень мелкого шага интегрирования по времени или дополнительных итераций. Поэтому предложенная явная схема предпочтительнее, особенно для численного исследования тонких структур и/или быстрых процессов.

Созданные алгоритмы и программное обеспечение предназначаются для вычислительных экспериментов в астрофизике и лабораторной астрофизике [13], для моделирования технологических процессов, связанных с использованием плотной лазерной плазмы, для исследований в области управляемого термоядерного синтеза.

Список литературы

Mihalas D., Mihalas B.W. Foundations of Radiation Hydrodynamics. Oxford Univ. Press, New York, 1984. 741 p.
Tolstov A.G., Blinnikov S.I., Nadyozhin D.K. Coupling of matter and radiation at supernova shock breakout // Monthly Notices of the Royal Astronomical Society. 2013. V. 429. Issue 4. P. 3181–3199. https://doi.org/10.1093/mnras/sts577
Четверушкин Б.Н., Ольховская О.Г. Моделирование процесса лучистой теплопроводности на высокопроизводительных вычислительных системах // Доклады Российской академии наук. Математика, информатика, процессы управления. 2020. Т. 491. № 1. С. 111–114. Chetverushkin B.N. and Olkhovskaya O.G. Modeling of Radiative Heat Conduction on High-Performance Computing Systems // Doklady Mathematics, 2020. V. 101. № 2, P. 172–175. https://doi.org/10.1134/S106456242002008810.1134/S1064562420020088https://doi.org/10.31857/S2686954320020083
Четверушкин Б.Н., Гулин А.В. Явные схемы и моделирование на вычислительных системах сверхвысокой производительности // Доклады Академии наук. 2012. Т. 446. № 5. С. 501–503. Chetverushkin B.N. and Gulin A.V. Explicit schemes and numerical simulation using ultrahigh-performance computer systems // Doklady Mathematics 2012. V. 86. № 2. P. 681–683. https://doi.org/10.1134/S1064562412050213
Mihalas D., Auer L. On laboratory-frame radiation hydrodynamics // Journal of Quantitative Spectroscopy and Radiative Transfer. 2001, V. 71. № 1. P. 61–97. https://doi.org/10.1016/S0022-4073(01)00013-9
Мышецкая Е.Е., Тишкин В.Ф. Оценки влияния гиперболизации для уравнения теплопроводности // Журнал вычислительной математики и математической физики. 2015. Т. 55. № 8. С. 1299. Myshets-kaya E.E., Tishkin V.F. Estimates of the hyperbolization effect on the heat equation // Computational Mathematics and Mathematical Physics. 2015. V. 55. P. 1270–1275. https://doi.org/10.1134/S096554251508013810.1134/S0965542515080138https://doi.org/10.7868/S004446691508013X
Репин С.И., Четверушкин Б.Н. Оценки разности приближенных решений задач Коши для параболического диффузионного уравнения и гиперболического уравнения с малым параметром // Доклады Академии наук. 2013. Т. 451. № 3. С. 255. Repin S.I. and Chetverushkin B.N. Estimates of the difference between approximate solutions of the cauchy problems for the parabolic diffusion equation and a hyperbolic equation with a small parameter // Doklady Mathematics. 2013. V. 88. № 1. P. 417–420. https://doi.org/10.1134/S106456241304015710.1134/S1064562413040157https://doi.org/10.7868/S0869565213210056
Сурначёв М.Д., Тишкин В.Ф., Четверушкин Б.Н. О законах сохранения для гиперболизированных уравнений // Дифференциальные уравнения. 2016. Т. 52. № 7. С. 859. Surnachev M.D., Tishkin V.F., Chetverushkin B.N. On conservation laws for hyperbolized equations // Differential Equations, 2016, V. 52. P. 817–823. https://doi.org/10.1134/S001226611607001610.1134/S0012266116070016https://doi.org/10.1134/S0374064116070013
Chetverushkin B.N. and Zlotnik A.A. On a hyperbolic perturbation of a parabolic initial–boundary value problem // Applied Mathematics Letters. 2018. V. 83. P. 116–122. https://doi.org/10.1016/j.aml.2018.03.027
Chetverushkin B.N., Olkhovskaya O.G., Tsigvintsev I.P. Numerical solution of high-temperature gas dynamics problems on high-performance computing systems // Journal of Computational and Applied Mathematics. 2021. V. 390. P. 113374https://doi.org/10.1016/j.cam.2020.113374
Глотов В.Ю., Головизнин В.М., Четверушкин Б.Н. Балансно-характеристические разностные схемы для уравнений параболического типа // Математическое моделирование. 2020. Т. 32. № 4. С. 94–106. Glotov V.Y., Goloviznin V.M. and Chetverushkin B.N. Balance and Characteristic Finite Difference Schemes for Equations of the Parabolic Type // Mathematical Models and Computer Simulations. 2020. V. 12. P. 981–989. https://doi.org/10.1134/S2070048220060095
Крайнов В.П. Качественные методы в физической кинетике и гидрогазодинамике. М.: Высшая школа, 1989. 224 с. Krainov V.P. Qualitative Methods in Physical Kinetics and Hydrodynamics. American Institute of Physics, 1992. 203 p.
Lebedev S.V., Frank A., Ryutov D.D. Exploring astrophysics-relevant magneto-hydrodynamics with pulsed-power laboratory facilities // Reviews of Modern Physics. 2019. V. 91 (2). 025002(46).https://doi.org/10.1103/RevModPhys.91.025002

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал