Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 506, № 1, стр. 41-44

ОБ ЭКВИВАЛЕНТНОСТИ ВЫРОЖДЕННЫХ И НЕКОРРЕКТНЫХ ЗАДАЧ. P-ФАКТОР МЕТОД РЕГУЛЯРИЗАЦИИ

Академик РАН Ю. Г. Евтушенко^1, 2, *, Е. Беднарчук⁴, А. Прусинска³, А. А. Третьяков^{1, 3, 4, **}

¹ Федеральный исследовательский центр “Информатика и управление” Российской академии наук
Москва, Россия

² Московский физико-технический институт
г. Долгопрудный, Московская область, Россия

³ Siedlce University, Faculty of Sciences
Siedlce, Poland

⁴ System Res. Inst., Polish Acad. Sciences
Warsaw, Poland

^* E-mail: yuri-evtushenko@yandex.ru
^** E-mail: prof.tretyakov@gmail.com

Поступила в редакцию 25.05.2022
После доработки 18.08.2022
Принята к публикации 20.08.2022

EDN: ZWBHCB
DOI: 10.31857/S2686954322050095

Полный текст (PDF)

Аннотация

В статье показывается локальная эквивалентность вырожденных и некорректных задач в классе достаточно гладких отображений, что обосновывает целесообразность применения так называемого p-фактор метода регуляризации для их решения. Описываются основные конструкции теории p-регулярности, необходимые для устойчивого решения приближенных задач и доказываются теоремы об оценках для регуляризирующих алгоритмов.

Ключевые слова: вырожденные и некорректные задачи, p-фактор метод

Рассмотрим задачу (уравнение)

(1)

$F(x) = 0,$

где $F:X \to Y$, $X$, $Y$ – банаховы пространства, F – достаточно гладкое отображение, ${{X}_{*}}$ = = $\{ x{\kern 1pt} *\, \in \,X\,{\text{|}}\,F(x{\kern 1pt} *)$ = 0} – множество решений уравнения (1). Наряду с (1) будем рассматривать приближенное уравнение

(2)

${{F}_{\varepsilon }}(x) = 0,$

где ${{F}_{\varepsilon }}(x) \to F(x)$ при $\varepsilon \to 0$, т.е. ${{F}_{\varepsilon }}$ – приближение отображения F. Пусть $U(x{\kern 1pt} *)$ – некоторая окрестность точки x*, а ${{F}_{0}}(x) \triangleq F(x)$. Введем

Опpеделение 1. Будем говорить, что задача (1) некорректна в точке x*, если существуют отображения ${{F}_{\varepsilon }}(x) \in {{C}^{1}}(X)$ такие, что для $\varepsilon > 0$ достаточно малых будет

(3)

$\begin{gathered} {\text{||}}{{F}_{\varepsilon }}(x) - F(x){\text{||}} \to 0,\quad {\text{||}}F_{\varepsilon }^{'}(x) - F{\kern 1pt} '(x){\text{||}} \to 0, \\ при\quad \varepsilon \to 0,\quad x \in U(x{\kern 1pt} *) \\ \end{gathered} $

– так называемое условие аппроксимации, но для множеств X(ε) = $\{ x(\varepsilon ) \in X\,{\text{|}}\,{{F}_{\varepsilon }}(x(\varepsilon )) = 0\} $ решений уравнения (2) существует последовательность $\{ {{\varepsilon }_{k}}\} $, ${{\varepsilon }_{k}} \to 0$ при $k \to \infty $ такая, что либо

$U(x{\kern 1pt} *) \cap X({{\varepsilon }_{k}}) = \emptyset ,$

либо

$\rho (X({{\varepsilon }_{k}}),{{X}_{*}}) \geqslant \Delta > 0,\quad при\quad k \to \infty .$

Задачу (1) мы будем называть идеальной, а задачу (2) ε-возмущенной (или ε-приближенной). Отображением F аналогично называем идеальным, а отображение ${{F}_{\varepsilon }}$ – $\varepsilon $-возмущенным (или ε-приближенным) отображением.

Опpеделение 2. Будем говорить, что задача (1) вырождена в точке x*, если $F{\kern 1pt} '(x{\kern 1pt} *)$ – вырождена, т.е. ${\text{Im}}\,F{\kern 1pt} '(x{\kern 1pt} *) \ne Y$.

Наряду с определением 1 введем понятие слабо некорректной задачи (1).

Опpеделение 3. Будем говорить, что задача (1) является слабо некорректной в точке x*, если существует отображение $\bar {F}(x) \in {{C}^{1}}(X)$ такое, что

(4)

${\text{|||}}F(x) - \bar {F}(x){\text{|}} = o({\text{||}}x - x{\kern 1pt} *{\text{||}})$

и задача $\bar {F}(x) = 0$ – некорректна.

Очевидно, что определению 3 удовлетворяет существенно более широкий класс отображений, чем определению 1. Отметим, что определение 1 некорректности фактически совпадает с классическим определением некорректности (см., например, [7]), за исключением добавленного здесь условия гладкости отображений и условия аппроксимации на производные $F_{\varepsilon }^{'}(x)$ и $F{\kern 1pt} '(x)$. Также рассматриваемый в статье класс задач существенно шире классического класса условно-корректных задач [7].

В реальной ситуации отображение F часто не известно, но известна его аппроксимация ${{F}_{\varepsilon }}$, поэтому такие проблемы мы называем обратными. Однако подразумевается, что идеальное отображение F существует (иначе нельзя говорить о решаемой задаче). Взаимосвязь между приближенными и вырожденными задачами в классе достаточно гладких отображений устанавливает следующий результат.

Теоpема 1. Пусть $F \in {{C}^{2}}(X)$ и $F(x{\kern 1pt} *) = 0$. Тогда задача (1) слабо некорректна в точке x* тогда и только тогда, когда задача (1) вырождена в точке x*.

Доказательство. Пусть задача (1) некорректна. Покажем, что отображение $F( \cdot )$ вырождено в точке x*. Действительно, если $F{\kern 1pt} '(x{\kern 1pt} *)$ не вырождена, то по теореме о неявной функции [1] применительно к отображениям $F(x,\varepsilon ) \triangleq {{F}_{\varepsilon }}(x)$, получаем существование $x(\varepsilon ) \in U(x{\kern 1pt} *)$ такого, что $F(x(\varepsilon ),\varepsilon )$ = 0 и $\rho (x(\varepsilon ),x{\kern 1pt} *) \leqslant K{\text{||}}F(x{\kern 1pt} *,\varepsilon ){\text{||}}$ → 0 при $\varepsilon \to 0$ равномерно по всем ${{F}_{\varepsilon }}(x)$, удовлетворяющих условию аппроксимации (3). Это, в свою очередь, означает корректность задачи (1).

Предположим теперь, что $F{\kern 1pt} '(x{\kern 1pt} *)$ вырождена. Тогда существует $\xi \in Y$ и 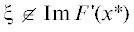, ${\text{||}}\xi {\text{||}} = 1$. Покажем, что задача (1) слабо некорректна. Рассмотрим отображения $\bar {F}(x) = F(x{\kern 1pt} *) + F{\kern 1pt} '(x{\kern 1pt} *)$(x – x*) и ${{\bar {F}}_{\varepsilon }}(x) = \bar {F}(x) + \varepsilon \xi $. Очевидно, что ${\text{||}}F(x) - \bar {F}(x){\text{||}}$ = = o(||x – x*||), но уравнение (2) ${{\bar {F}}_{\varepsilon }}(x) = 0$ не имеет решения при $x \in U(x{\text{*}})$, так как 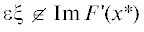, а $F{\kern 1pt} '(x{\kern 1pt} *)(x - x{\kern 1pt} *) \in {\text{Im}}\,F{\kern 1pt} '(x{\kern 1pt} *)$. То есть задача $\bar {F}(x) = 0$ не корректна, что означает слабую некорректность исходной задачи (1).

Следствие 1. Пусть F – линейное отображение $F \in {{C}^{1}}(X)$. Тогда задача (1) некорректна в точке $x{\kern 1pt} *$ тогда и только тогда, когда задача (1) вырождена в точке $x{\kern 1pt} *$.

Причем, если отображение F некорректно в точке x*, то $F{\kern 1pt} '(x{\kern 1pt} *)$ – вырожденно, а линейность нужна только при обратной импликации.

Таким образом, при решении приближенных задач целесообразно использовать методы, адаптированные для вырожденных задач, описание и основные конструкции которых предложены в теории p-регулярности (см., например, [2–4]).

1. ЭЛЕМЕНТЫ ТЕОРИИ p-РЕГУЛЯРНОСТИ

Будем рассматривать уравнение (1), причем отображение F вырождено в точке решения x*.

Пусть

(5)

$Y = {{Y}_{1}} \oplus \ldots \oplus {{Y}_{p}},$

где ${{Y}_{1}} = {\text{Cl}}({\text{Im}}\,F{\kern 1pt} '(x{\kern 1pt} *))$ и ${{Z}_{1}} = Y$. Через ${{Z}_{2}}$ обозначим замкнутое дополнение ${{Y}_{1}}$ до $Y$ (если такое существует) и ${{P}_{{{{Z}_{2}}}}}:Y \to {{Z}_{2}}$ – оператор проектирования на ${{Z}_{2}}$ параллельно ${{Y}_{1}}$. Тогда ${{Y}_{2}}$ – замыкание линейной оболочки образа квадратичной формы ${{P}_{{{{Z}_{2}}}}}F{\kern 1pt} '{\kern 1pt} '(x{\kern 1pt} *)[\, \cdot \,{{]}^{2}}$. И далее индуктивно

$\begin{gathered} {{Y}_{i}} = {\text{Cl}}({\text{span}}\,{\kern 1pt} {\text{Im}}\,{{P}_{{{{Z}_{i}}}}}{{F}^{{(i)}}}(x{\kern 1pt} *)[\, \cdot \,{{]}^{i}}) \subset {{Z}_{i}}, \\ i = 2, \ldots ,p - 1, \\ \end{gathered} $

где Z_i – замкнутое дополнение ${{Y}_{1}} \oplus \ldots \oplus {{Y}_{{i - 1}}}$ до Y и ${{P}_{{Z - i}}}:Y \to {{Z}_{i}}$ – операторы проектирования на Z_i параллельно ${{Y}_{1}} \oplus \ldots \oplus {{Y}_{{i - 1}}}$, $i = 1, \ldots ,p$. Окончательно, ${{Y}_{p}} = {{Z}_{p}}$. При этом порядок p выбирается как минимальное число (если такое существует), для которого выполнено представление (5).

Определим следующие отображения:

(6)

${{F}_{i}}:X \to {{Y}_{i}},\quad {{F}_{i}}(x) = {{P}_{{{{Y}_{i}}}}}F(x),\quad i = 1, \ldots ,p,$

где ${{P}_{{{{Y}_{i}}}}}:Y \to {{Y}_{i}}$ оператор проектирования на ${{Y}_{i}}$ параллельно ${{Y}_{1}} \oplus \ldots \oplus {{Y}_{{i - 1}}} \oplus {{Y}_{{i + 1}}} \oplus \ldots \oplus {{Y}_{p}}$. Тогда отображение F может быть представлено как

$F(x) = {{F}_{1}}(x) + \ldots + {{F}_{p}}(x)$

или в векторном виде

$F(x) = \left( {{{F}_{1}}(x), \ldots ,{{F}_{p}}(x)} \right).$

Опpеделение 4. Линейный оператор Ψ_p = = ${{\Psi }_{p}}(h):X \to Y$

(7)

${{\Psi }_{p}}(h) = F_{1}^{'}(x{\kern 1pt} *) + F_{2}^{{''}}(x{\kern 1pt} *)[h] + \ldots + F_{p}^{{(p)}}(x{\kern 1pt} *)[h{{]}^{{p - 1}}}$

называется p-фактор оператором, определенным элементом h, или просто p-фактор оператором, если это ясно из контекста.

Введем в рассмотрение нелинейный оператор ${{\Psi }_{p}}{{[ \cdot ]}^{p}}$ так, что

${{\Psi }_{p}}{{[x]}^{p}} = F_{1}^{'}(x{\kern 1pt} *)[x] + F_{2}^{{''}}(x{\kern 1pt} *)[x{{]}^{2}} + \ldots + F_{p}^{{(p)}}(x{\kern 1pt} *)[x{{]}^{p}}.$

Заметим, что ${{\Psi }_{p}}{{[x]}^{p}} = {{\Psi }_{p}}(x)[x]$.

Опpеделение 5. $p$-ядро оператора ${{\Psi }_{p}}$ есть множество

$\begin{gathered} {{H}_{p}}(x{\kern 1pt} *) = {\text{Ke}}{{{\text{r}}}^{p}}{{\Psi }_{p}} = \{ z \in X\,{\text{|}}\,F_{1}^{'}(x{\kern 1pt} *)[z] + \\ \, + F_{2}^{{''}}(x{\kern 1pt} *)[z{{]}^{2}} + \ldots + F_{p}^{{(p)}}(x{\kern 1pt} *)[z{{]}^{p}} = 0\} . \\ \end{gathered} $

Заметим, что ${\text{Ker}}{{{\kern 1pt} }^{p}}{{\Psi }_{p}} = \cap _{{k = 1}}^{p}{\text{Ker}}{{{\kern 1pt} }^{k}}F_{k}^{{(k)}}(x{\kern 1pt} *)$, где ${\text{Ker}}{{{\kern 1pt} }^{k}}F_{k}^{{(k)}}( \cdot ) = \{ z \in X\,{\text{|}}\,{{F}^{{(k)}}}( \cdot )[z{{]}^{k}} = 0\} $ – k-ядро отображения ${{F}^{{(k)}}}( \cdot )[ \cdot {{]}^{k}}$.

Опpеделение 6. Отображение F называется p-регулярным в точке x* на элементе h, если ${\text{Im}}\,{{\Psi }_{p}}(h) = Y$.

Опpеделение 7. Отображение F называется p-регулярным в точке x*, если оно p-регулярно на каждом элементе $h \in {{H}_{p}}(x{\kern 1pt} *){{\backslash }}\{ 0\} $ или ${{H}_{p}}(x{\kern 1pt} *) = \{ 0\} $.

2. p-ФАКТОР МЕТОД РЕШЕНИЯ ВЫРОЖДЕННЫХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Рассмотрим уравнение (1) при $X = {{\mathbb{R}}^{n}}$ и Y = ${{\mathbb{R}}^{n}}$ в случае вырождения $F{\kern 1pt} '(x{\kern 1pt} *)$ в решении x*. Тогда принципиальная схема p-фактор метода будет следующая:

${{x}_{{k + 1}}} = {{x}_{k}} - $

(8)

$\begin{gathered} \, - {{\{ F{\kern 1pt} '({{x}_{k}}) + {{P}_{2}}F{\kern 1pt} '{\kern 1pt} '({{x}_{k}})h + \ldots + {{P}_{p}}{{F}^{p}}({{x}_{k}}){{h}^{{p - 1}}}\} }^{{ - 1}}} \cdot \\ \, \cdot (F({{x}_{k}}) + {{P}_{2}}F{\kern 1pt} '({{x}_{k}})h + \ldots + {{P}_{p}}{{F}^{{(p - 1)}}}({{x}_{k}}){{h}^{{p - 1}}}), \\ \end{gathered} $

$k = 0,1,2, \ldots ,$

где ${{P}_{i}} = {{P}_{{{{Y}_{i}}}}}$, $i = 1, \ldots ,p$ и элемент h, ${\text{||}}h{\text{||}} = 1$ выбирается таким образом, что p-фактор оператор ${{\Psi }_{p}}(h)\, = \,F{\kern 1pt} '(x{\kern 1pt} *)$ + ${{P}_{2}}F{\kern 1pt} '{\kern 1pt} '(x{\kern 1pt} *)h + \ldots + {{P}_{p}}{{F}^{{(p)}}}(x{\kern 1pt} *){{h}^{{p - 1}}}$ был невырожденным, что означает p-регулярность отображения F в точке x* на элементе h.

Для p-фактор метода (8) будет справедлива следующая

Теоpема 2. Пусть $F \in {{C}^{{p + 1}}}({{\mathbb{R}}^{n}})$ и существует элемент h, ${\text{||}}h{\text{||}} = 1$ такой, что p-фактор оператор ${{\Psi }_{p}}(h)$ не вырожден. Тогда для ${{x}_{0}} \in {{U}_{\varepsilon }}(x{\kern 1pt} *)$ ($\varepsilon > 0$ – достаточно малое), последовательность $\{ {{x}_{k}}\} $, определенная схемой (8) , сходится к решению x* и верна оценка скорости сходимости

(9)

${\text{||}}{{x}_{{k + 1}}} - x{\kern 1pt} *{\text{||}} \leqslant C{\text{||}}{{x}_{k}} - x{\kern 1pt} *{\text{|}}{{{\text{|}}}^{2}},\quad k = 0,1,2, \ldots ,$

где $C > 0$ – независимая константа.

3. $p$-ФАКТОР МЕТОД РЕГУЛЯРИЗАЦИИ ($p$-ФАКТОР РЕГУЛЯРИЗАЦИЯ)

Пусть x* является решением идеальной задачи (уравнения) (1). При этом регулярность (не вырожденность) F в точке x* не предполагается. Одновременно рассматриваем приближенное уравнение

(10)

$\widetilde F(x) = 0,$

${\text{||}}\widetilde F(x) - F(x){\text{||}} \leqslant \varepsilon $, где $\varepsilon > 0$ – достаточно малое и $x \in U(x{\kern 1pt} *)$. При этом считаем $\widetilde F \in {{C}^{{p + 1}}}(X)$. Основная идея p-фактор регуляризации состоит в следующем. Нужно заменить уравнение (1) другим уравнением, которое гарантированно имело бы x* своим решением и было бы невырождено в точке x*. Здесь предлагается реализация данной идеи, основанной на конструкции p-регулярности. Базовым результатом является

Теоpема 3. Пусть $X$, $Y$ – банаховы пространства, $F$, $\widetilde F \in {{C}^{{p + 1}}}(X,Y)$, $F(x{\kern 1pt} *) = 0$ и $F$ – p-регулярно на элементе $h \in X$, $h \ne 0$, причем

${\text{||}}{{\widetilde F}^{{(k)}}}(x) - {{F}^{{(k)}}}(x){\text{||}} \leqslant \varepsilon ,\quad k = 0,1, \ldots ,p + 1,$

$\forall x \in U(x{\kern 1pt} *)$, где $\varepsilon > 0$ – достаточно малое, а $U(x{\kern 1pt} *)$ – некоторая окрестность точки x*.

Тогда отображение ${{\Phi }_{{\widetilde F}}}(x)$

${{\Phi }_{{\widetilde F}}}(x) = \widetilde F(x) + {{P}_{2}}\widetilde F'(x)h + \ldots + {{P}_{p}}{{\widetilde F}^{{(p - 1)}}}(x){{h}^{{p - 1}}}$

является p-фактор регуляризующим для приближенного уравнения (10), т.е.

(11)

$\Phi _{{\widetilde F}}^{{ - 1}}(0) \ne \emptyset $

(12)

$\begin{gathered} \rho (x{\kern 1pt} *,\Phi _{{\widetilde F}}^{{ - 1}}(0)) \leqslant \\ \, \leqslant {\text{||}}\widetilde F(x{\kern 1pt} *) + {{P}_{2}}\widetilde F'(x{\kern 1pt} *)h + \ldots + {{P}_{p}}{{\widetilde F}^{{(p - 1)}}}(x{\kern 1pt} *){{h}^{{p - 1}}}{\text{||}} \leqslant \\ \, \leqslant C \cdot \varepsilon . \\ \end{gathered} $

Здесь через $\Phi _{{\widetilde F}}^{{ - 1}}(0)$ обозначим прообраз точки $y = 0$ для отображения ${{\Phi }_{{\widetilde F}}}(x)$, т.е. $\Phi _{{\widetilde F}}^{{ - 1}}(0)$ = = $\{ x \in X\,{\text{|}}\,{{\Phi }_{{\widetilde F}}}(x)$ = 0}.

Замечание 1. Если p-фактор оператор $F{\kern 1pt} '(x{\kern 1pt} *) + {{P}_{2}}F{\kern 1pt} '{\kern 1pt} '(x{\kern 1pt} *)h + \ldots + {{P}_{p}}{{F}^{{(p)}}}(x{\kern 1pt} *){{h}^{{p - 1}}}$ биективен, то существует локально единственное решение уравнения (10): $\widetilde F(x) = 0$ в окрестности $U(x{\kern 1pt} *)$, которое мы обозначим через $\tilde {x}$. Тогда основной результат выглядит следующим образом

(13)

${{\Phi }_{{\widetilde F}}}(\tilde {x}) = 0$

(14)

$\rho (x{\kern 1pt} *,\tilde {x}) \leqslant C \cdot \varepsilon .$

Например, условие биекции заведомо будем выполнено, если X, Y – конечномерные евклидовы пространства одинаковой размерности.

Доказательство. Обозначим $\Phi (\widetilde F,x)$ = = ${{\Phi }_{{\widetilde F}}}(x)$. Тогда, применяя классическую теорему о неявной функции [1] к отображению $\Phi (\widetilde F,x)$ в точке $\widetilde F = F$ и $x = x{\kern 1pt} *$, получаем, что оператор $\Phi _{x}^{'}(F,x{\kern 1pt} *)$ не вырожден в этой точке $(F,x{\kern 1pt} *)$ и, следовательно, существует функция $x = x(\widetilde F)$, которая является локальным решением уравнения $\Phi (\widetilde F,x(\widetilde F))) = {{\Phi }_{{\widetilde F}}}(x(\widetilde F)) = 0$ и справедливы оценки (12) и (14), т.к. ${\text{||}}x(\widetilde F) - x{\kern 1pt} *{\text{||}} \leqslant C{\text{||}}\Phi (\widetilde F,x{\kern 1pt} *){\text{||}}$ для $C > 0$ – независимой констранты.

Использование в конструкции отображения $\Phi ( \cdot )$ точных операторов P_k, $k = 1, \ldots ,p - 1$ сделано заведемо специально, так как этот аспект не является главным в идеологии предложенного подхода, а скорее техническим в практической реализации метода. Тем более, что уже существуют способы построения операторов P_k, $k = 1, \ldots ,p - 1$ на основе приближенной информации (см., например, [5, 6]). В общем случае построение операторов P_k или их приближений с нужными свойствами требует использования специфики рассматриваемой задачи (см. [2]).

Список литературы

Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М.: Наука, 1979.
Измаилов А.Ф., Третьяков А.А. 2-регулярные решения нелинейных задач. Теория и численные методы. М.: Физико-математическая литература, 1999.
Измаилов A.Ф., Третьяков А.А. Фактор-анализ нелинейных отображений. М.: Наука, 1994.
Tret’yakov A., Marsden J.E. Factor analysis of nonlinear mappings: p-regularity theory //Communications on Pure & Applied Analysis. 2003. V. 2. № 4. P. 425–445.
Брежнева О.А., Третьяков А.А. Методы решения существенно нелинейных задач. М.: ВЦ РАН, 2000.
Szczepanik E., Tret’yakov A. Teoria P-regularności i metody rorwiązywania nieliniowych problemów optymalizacji. Siedlce: Uniwersytet Przyrodniczo Humanistyczny w Siedlcach, 2020. (на польском языке)
Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Из-во СО РАН, 2018.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал