Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 506, № 1, стр. 62-67

О СОВМЕСТНОМ МОДЕЛИРОВАНИИ ВОЛНОВЫХ ЯВЛЕНИЙ СЕТОЧНО-ХАРАКТЕРИСТИЧЕСКИМ МЕТОДОМ И РАЗРЫВНЫМ МЕТОДОМ ГАЛЕРКИНА

Член-корреспондент РАН И. Б. Петров^1, *, А. В. Фаворская^1, **

¹ Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

^* E-mail: petrov@mipt.ru
^** E-mail: favorskaya@phystech.edu

Поступила в редакцию 23.09.2021
После доработки 13.07.2022
Принята к публикации 03.08.2022

EDN: JVFUUD
DOI: 10.31857/S2686954322050150

Полный текст (PDF)

Аннотация

Целью работы являлась разработка гибридного численного метода, объединяющего сеточно-характеристический метод на структурированных регулярных сетках с разрывным методом Галеркина на неструктурированных тетраэдральных сетках. Предложенный метод позволяет описывать сложную форму границ и контактных границ области интегрирования, в том числе, выполнять расчет сейсмических полей с учетом топографии поверхности Земли, и при этом экономить вычислительные ресурсы. Данная модификация численных методов в трехмерной постановке впервые предложена в данной работе. Приведены примеры использования разработанного метода для расчета возникающих при сейсмической разведке упругих волновых явлений. Для тестирования было проведено сравнение с расчетом сеточно-характеристическим методом на структурированных криволинейных сетках. Предложенный гибридный численный метод может применяться не только для задач сейсмической разведки, но и для расчета волновых явлений в других объектах сложной формы.

Ключевые слова: математическое моделирование, сеточно-характеристический метод, разрывный метод Галеркина, сейсморазведка, тетраэдральные сетки, комбинирование численных методов, учет топографии поверхности, криволинейные структурированные сетки

В наши дни поиск и уточнение запасов углеводородов требуют применения вычислительных методов для обработки данных сейсмической разведки [1, 2]. В том числе необходима разработка высокоточных методов прямого численного моделирования волновых явлений в геологических средах.

Наиболее часто употребимыми современными методами моделирования распространения упругих волн являются различные модификации конечно-разностных методов [3, 4], метод спектральных элементов [5, 6] и разрывный метод Галеркина [7, 8]. Сеточно-характеристический метод также успешно применим для моделирования упругих волн в геологических породах [9, 10]. Кроме того, разрабатывают и гибридные подходы [11–13].

В данной работе предложено использовать сеточно-характеристический метод на структурированных расчетных сетках с постоянными шагами интегрирования по координатам [10] совместно с разрывным методом Галеркина на тетраэдральных сетках. Где это возможно, используются структурированные расчетные сетки и сеточно-характеристический метод, а рядом с границами и контактными границами криволинейной формы применяется тетраэдральная сетка и используется разрывный метод Галеркина.

Для моделирования распространения сейсмических волн в геологических породах ищется решение следующей начально-краевой задачи упругого волнового уравнения:

(1)

${{\rho }}\frac{\partial }{{\partial t}}{\mathbf{v}}\left( {{\mathbf{r}},t} \right) = {{\left( {\nabla \cdot {\mathbf{\sigma }}\left( {{\mathbf{r}},t} \right)} \right)}^{{\text{T}}}},$

(2)

$\begin{gathered} \frac{\partial }{{\partial t}}{\mathbf{\sigma }}\left( {{\mathbf{r}},t} \right) = ({{\rho }}c_{{\text{P}}}^{{\text{2}}} - 2{{\rho }}c_{{\text{S}}}^{{\text{2}}})\left( {\nabla \cdot {\mathbf{v}}\left( {{\mathbf{r}},t} \right)} \right)I + \\ \, + {{\rho }}c_{{\text{S}}}^{{\text{2}}}(\nabla \otimes {\mathbf{v}}\left( {{\mathbf{r}},t} \right) + {{\left( {\nabla \otimes {\mathbf{v}}\left( {{\mathbf{r}},t} \right)} \right)}^{{\text{T}}}}). \\ \end{gathered} $

Здесь ${\mathbf{v}}\left( {{\mathbf{r}},t} \right)$ − скорость (производная смещения), ${\mathbf{\sigma }}\left( {{\mathbf{r}},t} \right)$ − симметричный тензор напряжений Коши, ${\mathbf{r}}$ − радиус-вектор, $t$ − время, $\nabla $ − вектор-градиент, ${{\rho }}$ − плотность, ${{c}_{{\text{P}}}}$, ${{c}_{{\text{S}}}}$ − скорости продольных и поперечных волн соответственно, $I$ − единичный тензор второго ранга, $ \otimes $ − тензорное произведение векторов, ${{\left( {{\mathbf{a}} \otimes {\mathbf{b}}} \right)}_{{ij}}} = {{a}_{i}}{{b}_{j}}$.

На поверхности Земли ставилось условие свободной границы, на всех остальных внешних границах области интегрирования – неотражающие граничные условия. В качестве источника сейсмических волн рассматривались точечный источник и импульс Риккера с частотой 20 Гц.

Рассмотрим подробнее расчет решения системы (1), (2) в точках между на границах между подобластями, в которых используются сеточно-характеристический метод и разрывный метод Галеркина.

При использовании сеточно-характеристического метода вначале выполняется расщепление по пространственным координатам. Затем выполняют переход к инвариантам Римана каждой из трех полученных одномерных гиперболических систем уравнений, используя следующие выражения:

${{\omega }_{{1,2}}} = {{{\mathbf{n}}}_{0}} \cdot {\mathbf{v}} \mp \frac{1}{{{{c}_{{\text{P}}}}\rho }}{{{\mathbf{N}}}_{{00}}} \div {\mathbf{\sigma }}$

${{\omega }_{{3,4}}} = {{{\mathbf{n}}}_{1}} \cdot {\mathbf{v}} \mp \frac{1}{{{{c}_{{\text{S}}}}\rho }}{{{\mathbf{N}}}_{{01}}} \div {\mathbf{\sigma }}$

${{\omega }_{{5,6}}} = {{{\mathbf{n}}}_{2}} \cdot {\mathbf{v}} \mp \frac{1}{{{{c}_{{\text{S}}}}\rho }}{{{\mathbf{N}}}_{{02}}} \div {\mathbf{\sigma }}$

${{\omega }_{7}} = {{{\mathbf{N}}}_{{12}}} \div {\mathbf{\sigma }}$

${{\omega }_{8}} = \left( {{{{\mathbf{N}}}_{{11}}} - {{{\mathbf{N}}}_{{22}}}} \right) \div {\mathbf{\sigma }}$

${{\omega }_{9}} = \left( {{{{\mathbf{N}}}_{{11}}} + {{{\mathbf{N}}}_{{22}}} - 2\left( {1 - 2\frac{{c_{{\text{S}}}^{2}}}{{c_{{\text{P}}}^{2}}}} \right){{{\mathbf{N}}}_{{00}}}} \right) \div {\mathbf{\sigma }}.$

Здесь n₀ – единичный вектор, направленный вдоль рассматриваемой оси координат, n₁, n₂ образуют с ним правый базис, N_ij = $\frac{1}{2}({{{\mathbf{n}}}_{i}}\, \otimes \,{{{\mathbf{n}}}_{j}}\, + \,{{{\mathbf{n}}}_{j}}\, \otimes \,{{{\mathbf{n}}}_{i}})$, ${{\left( {{\mathbf{A}} \div {\mathbf{B}}} \right)}_{{ij}}}$ = $\sum\limits_{p,q} {{{A}_{{ip}}}{{B}_{{qj}}}} $.

Затем решают полученные уравнения переноса с набором коэффициентов $\{ {{с}_{{\text{P}}}}, - {{с}_{{\text{P}}}},{{с}_{{\text{S}}}}, - {{с}_{{\text{S}}}},{{с}_{{\text{S}}}}, - {{с}_{{\text{S}}}}$, 0, 0, 0} с использованием их характеристических свойств, и выполняют обратный переход к неизвестным функциям ${\mathbf{v}}\left( {{\mathbf{r}},t} \right)$ и ${\mathbf{\sigma }}\left( {{\mathbf{r}},t} \right)$, используя следующие выражения:

${\mathbf{v}} = \frac{1}{2}\left( {\left( {{{\omega }_{1}} + {{\omega }_{2}}} \right){{{\mathbf{n}}}_{0}} + \left( {{{\omega }_{3}} + {{\omega }_{4}}} \right){{{\mathbf{n}}}_{1}} + \left( {{{\omega }_{5}} + {{\omega }_{6}}} \right){{{\mathbf{n}}}_{2}}} \right)$

$\begin{gathered} {\mathbf{\sigma }} = \frac{1}{2}\left\{ {{{с}_{{\text{P}}}}\rho \left( {{{\omega }_{2}} - {{\omega }_{1}}} \right)\left( {2\frac{{c_{{\text{S}}}^{2}}}{{c_{{\text{P}}}^{2}}}{{{\mathbf{N}}}_{{00}}} + \left( {1 - 2\frac{{c_{{\text{S}}}^{2}}}{{c_{{\text{P}}}^{2}}}} \right){\mathbf{I}}} \right) + } \right. \\ \, + 2{{с}_{{\text{S}}}}\rho \left( {{{\omega }_{4}} - {{\omega }_{3}}} \right){{{\mathbf{N}}}_{{01}}} + 2{{с}_{{\text{S}}}}\rho \left( {{{\omega }_{6}} - {{\omega }_{5}}} \right){{{\mathbf{N}}}_{{02}}} + \\ \left. {\, + 4{{\omega }_{7}}{{{\mathbf{N}}}_{{12}}} + {{\omega }_{8}}\left( {{{{\mathbf{N}}}_{{11}}} - {{{\mathbf{N}}}_{{22}}}} \right) + \omega _{9}^{{^{{^{{^{{}}}}}}}}\left( {{\mathbf{I}} - {{{\mathbf{N}}}_{{00}}}} \right)} \right\} \\ \end{gathered} $

При использовании разрывного метода Галеркина функции неизвестных раскладывают по выбранному базису ортогональных функций ${{\Phi }_{i}}(\xi ,\eta ,\varsigma )$ в единичном тетраэдре ${{T}_{{\text{E}}}}$

(3)

$\begin{gathered} u_{k}^{m}\left( {x,y,z,t} \right) = \\ \, = \sum\limits_{l = 1}^{10} {u_{{kl}}^{m}\left( t \right) \cdot {{\Phi }_{l}}({{{{\xi }}}^{m}}\left( {x,y,z} \right),{{{{\eta }}}^{m}}\left( {x,y,z} \right),{{{{\varsigma }}}^{m}}\left( {x,y,z} \right))} \\ \end{gathered} $

и получают полудискретную форму записи системы (1), (2):

$\begin{gathered} \frac{{\partial u_{{pl}}^{{\left( m \right)}}}}{{\partial t}}\left| J \right|\int\limits_{{{T}_{{\text{E}}}}} {{{\Phi }_{l}}{{\Phi }_{k}}d\Omega } + \sum\limits_{j = 1}^4 {F_{{pl}}^{{h,j, - }}\left| {{{S}_{j}}} \right|} \int\limits_{{{{\left( {\partial {{T}_{{\text{E}}}}} \right)}}_{j}}} {{{\Phi }_{l}}{{\Phi }_{k}}ds} + \\ \, + \sum\limits_{j = 1}^4 {F_{{pl}}^{{h,j, + }}\left| {{{S}_{j}}} \right|} \int\limits_{{{{\left( {\partial {{T}_{{\text{E}}}}} \right)}}_{j}}} {{{\Phi }_{l}}{{\Phi }_{k}}ds} - \\ \end{gathered} $

(4)

$\, - A_{{pq}}^{*}u_{{pl}}^{{\left( m \right)}}\left| J \right|\int\limits_{{{T}_{{\text{E}}}}} {{{\Phi }_{l}}\frac{{\partial {{\Phi }_{k}}}}{{\partial \xi }}d\Omega } - $

$\begin{gathered} \, - B_{{pq}}^{*}u_{{pl}}^{{\left( m \right)}}\left| J \right|\int\limits_{{{T}_{{\text{E}}}}} {{{\Phi }_{l}}\frac{{\partial {{\Phi }_{k}}}}{{\partial \eta }}d\Omega } - \\ \, - C_{{pq}}^{*}u_{{pl}}^{{\left( m \right)}}\left| J \right|\int\limits_{{{T}_{{\text{E}}}}} {{{\Phi }_{l}}\frac{{\partial {{\Phi }_{k}}}}{{\partial \varsigma }}d\Omega } = 0. \\ \end{gathered} $

Здесь $u_{{pl}}^{{\left( m \right)}}$ – коэффициенты в разложении решения по базису ортогональных функций в тетраэдре m, причем первый индекс соответствует компоненте вектора неизвестных, $\left| J \right|$ – якобиан из координат узлов рассматриваемого тетраэдра, $F_{{pl}}^{{h,j, - }}$ и $F_{{pl}}^{{h,j, + }}$ – выходящий и входящий потоки, $\left| {{{S}_{j}}} \right|$ – площадь j-й грани тетраэдра ${{\left( {\partial {{T}_{E}}} \right)}_{j}}$, матрицы $A_{{pq}}^{*}$, $B_{{pq}}^{*}$ и $C_{{pq}}^{*}$ выражаются через коэффициенты решаемой гиперболической системы уравнений (1), (2) и координаты рассматриваемого тетраэдра. В уравнении (4) интегралы вычисляются аналитически и заранее, так как набор ортогональных базисных функций известен, а итоговую систему решают итерационным методом по времени, например, методами Рунге–Кутты.

Ниже приведем метод вычисления решения вблизи границы между подобластями, в которых используются разрывный метод Галеркина на тетраэдральных сетках и сеточно-характеристический метод на регулярных сетках.

В предположении об одинаковой ориентации тетраэдров вдоль данной границы с регулярной сеткой можно получить следующее упрощенное выражение для входящих потоков граничных тетраэдров:

$\begin{gathered} F_{{pl}}^{{h,1, + }}\left| {{{S}_{1}}} \right|\int\limits_{{{{\left( {\partial {{T}_{{\text{E}}}}} \right)}}_{1}}} {{{\Phi }_{l}}{{\Phi }_{k}}ds} = \\ \, = \left| {{{S}_{1}}} \right|G_{{pa}}^{{1, + }}{{\left( {{{{\mathbf{u}}}_{{{{d}_{{\text{X}}}},{{d}_{{\text{Y}}}}}}}} \right)}_{a}}\int\limits_0^1 {d\xi \int\limits_0^{1 - \xi } {{{\Phi }_{k}}\left( {\xi ,\eta ,0} \right)} } d\eta \pm \\ \, \pm \left| {{{S}_{1}}} \right|G_{{pa}}^{{1, + }}\left( {{{{\left( {{{{\mathbf{u}}}_{{{{d}_{{\text{X}}}} \pm 1,{{d}_{{\text{Y}}}}}}}} \right)}}_{a}} - {{{\left( {{{{\mathbf{u}}}_{{{{d}_{{\text{X}}}},{{d}_{{\text{Y}}}}}}}} \right)}}_{a}}} \right) \times \\ \end{gathered} $

$\begin{gathered} \, \times \int\limits_0^1 {\xi d\xi \int\limits_0^{1 - \xi } {{{\Phi }_{k}}\left( {\xi ,\eta ,0} \right)} } d\eta \pm \\ \, \pm \left| {{{S}_{1}}} \right|G_{{pa}}^{{1, + }}\left( {{{{\left( {{{{\mathbf{u}}}_{{{{d}_{{\text{X}}}},{{d}_{{\text{Y}}}} \pm 1}}}} \right)}}_{a}} - {{{\left( {{{{\mathbf{u}}}_{{{{d}_{{\text{X}}}},{{d}_{{\text{Y}}}}}}}} \right)}}_{a}}} \right) \times \\ \, \times \int\limits_0^1 {\eta d\eta \int\limits_0^{1 - \eta } {{{\Phi }_{k}}\left( {\xi ,\eta ,0} \right)d\xi } } \\ \end{gathered} $

$G_{{pa}}^{{1, + }} = T_{{pq}}^{{{{m}_{1}}}}\frac{1}{2}{{R}_{{qb}}}({{\Lambda }_{{br}}} - \,{\text{|}}{{\Lambda }_{{br}}}{\text{|}})R_{{rs}}^{{ - 1}}{{(T_{{sa}}^{{{{m}_{1}}}})}^{{ - 1}}}$

Здесь $T_{{pq}}^{{{{m}_{j}}}}$ – матрица поворота j-й грани, ${{R}_{{qb}}}$ – матрица, составленная из собственных векторов рассматриваемой гиперболической системы (1), (2), ${{\Lambda }_{{br}}}\, = \,{\text{diag}}\left\{ { - {{с}_{{\text{P}}}}, - {{с}_{{\text{S}}}}, - {{с}_{{\text{S}}}},0,0,0,{{с}_{{\text{S}}}},{{с}_{{\text{S}}}},{{с}_{{\text{P}}}}} \right\}$, ${{({{{\mathbf{u}}}_{{{{d}_{{\text{X}}}},{{d}_{{\text{Y}}}}}}})}_{a}}$ – a-я компонента вектора неизвестных ${\mathbf{u}}$ в точке регулярной сетки с индексами ${{d}_{{\text{X}}}}$, ${{d}_{{\text{Y}}}}$ по осям OX, OY соответственно. Причем точки $\left\{ {{{d}_{{\text{X}}}},{{d}_{{\text{Y}}}}} \right\}$, $\left\{ {{{d}_{{\text{X}}}} \pm 1,{{d}_{{\text{Y}}}}} \right\}$, $\left\{ {{{d}_{{\text{X}}}},{{d}_{{\text{Y}}}} \pm 1} \right\}$ совпадают с точками горизонтальной грани тетраэдра.

А для расчета неизвестных функций ${\mathbf{v}}\left( {{\mathbf{r}},t} \right)$ и ${\mathbf{\sigma }}\left( {{\mathbf{r}},t} \right)$ сеточно-характеристическим методом необходимо знать их значения вдоль характеристик, попадающих в зону тетраэдральной сетки. Эти значения вдоль характеристик восстанавливаются по формуле (3) в граничном тетраэдре, в который попадает рассматриваемая характеристика.

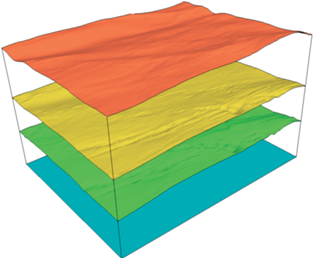
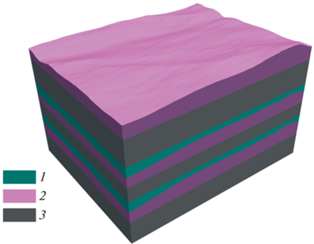
Далее мы приводим результаты тестовых расчетов. На рис. 1, 2 изображена трехмерная геологическая модель, с использованием которой проводились тестовые расчеты. На рис. 1 изображены границы раздела геологических пород, а на рис. 2 приведено распределение скорости продольных волн. Соответствующие распределения остальных упругих параметров можно найти в табл. 1.

Рис. 1.

Геологическая модель, границы раздела геологических пород.

Рис. 2.

Геологическая модель, распределение скорости продольных волн.

Таблица 1.

Отдельные расчетные сетки, типы рассматриваемых сред, упругие параметры каждого слоя геологической породы

Слой	Скорость продольных волн, м/c	Скорость поперечных волн, м/c	Плотность, кг/м³
1	2000	1000	2000
2	2700	1300	2200
3	3600	1700	2500

Таблица 2.

Результаты исследования сходимости сеточно-характеристического метода на криволинейных структурированных расчетных сетках [9]

Шаг по координате, м	Ошибка по норме L₁	Ошибка по норме L_∞	Порядок сходимости по норме L₁	Порядок сходимости по норме L_∞
25	4927	0.249	–	–
12.5	1460	0.076	1.755	1.720
6.25	440	0.023	1.730	1.713
3.125	132	0.007	1.733	1.712

Таблица 3.

Результаты исследования сходимости предложенного в работе комбинированного метода

Шаг по координате, м	Ошибка по норме L₁	Ошибка по норме L_∞	Порядок сходимости по норме L₁	Порядок сходимости по норме L_∞
25	5145	0.280	–	–
12.5	1258	0.067	2.032	2.070
6.25	339	0.019	1.890	1.807
3.125	92	0.005	1.879	1.809

На рис. 3 изображены тетраэдральные расчетные сетки, прилегающие к поверхности Земли и криволинейным границам раздела геологических пород, и регулярные расчетные сетки. Шаг сетки вдоль направлений OX и OY брался равным 12.5 м, вдоль OZ – 10 м в регулярных сетках и приблизительно 10 м в криволинейных структурированных сетках. Шаг по времени брался равным 0.4 мс, было выполнено 2800 шагов по времени в обоих расчетах.

Рис. 3.

Тетраэдральные (1, 2) и структурированные регулярные (3) расчетные сетки при использовании комбинированного метода.

На рис. 4, 5 представлен результат визуализации волновых полей модуля скорости (волновые картины [14]). Результаты на рис. 4 получены с помощью комбинированного метода, а результаты на рис. 5 – с помощью сеточно-характеристического метода на криволинейных структурированных сетках [9].

Рис. 4.

Волновая картина модуля скорости, расчет с помощью совместного использования сеточно-характеристического метода на регулярных сетках и разрывного метода Галеркина на тетраэдральных сетках.

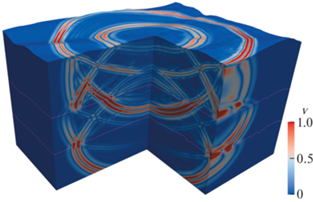
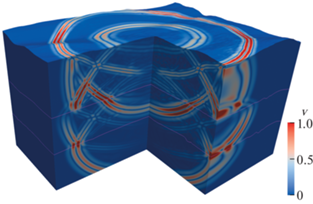
Рис. 5.

Волновая картина модуля скорости, расчет с помощью сеточно-характеристического метода на криволинейных структурированных сетках.

В табл. 2, 3 приведены результаты исследования на сходимость предложенного в настоящей работе комбинированного метода и сеточно-характеристического метода на криволинейных структурированных расчетных сетках, а в табл. 4 – соответствующие затраты оперативной памяти и времени на вычисления. Под шагом по координате мы понимали шаг в регулярных расчетных сетках для комбинированного метода и шаг вдоль осей OX и OY для метода на криволинейных структурированных сетках (так как в рассматриваемой постановке задачи он брался фиксированным). Тестирование проводилось для числа Куранта 0.4. Можно видеть, что при достаточно крупном шаге интегрирования предложенный комбинированный метод еще не дает выигрыша по затратам вычислительных ресурсов, но при дальнейшем измельчении расчетной сетки доля объема вблизи криволинейных границ, разбиваемого на тетраэдры, уменьшается, и затраты становятся меньше. Также предложенный комбинированный метод обладает более высоким порядком сходимости по обеим нормам.

Таблица 4.

Сравнение затрат вычислительных ресурсов

Шаг по координате, м	Сеточно-характеристический метод на структурированных криволинейных сетках [9]		Предложенный в работе комбинированный метод
Шаг по координате, м	Затраты оперативной памяти, Гб	Затраты времени на вычисления	Затраты оперативной памяти, Гб	Затраты времени на вычисления
25	0.56	11 мин	1.808	41 мин
12.5	4.16	2 ч 43 мин	7.616	5 ч
6.25	33.8	1 день 19 ч	27.9	1 день 11 ч
3.125	241.7	30 дней 6 ч	170.5	20 дней 15 ч

Полученные результаты численных экспериментов позволяют сделать вывод о перспективах применения разработанного численного метода для высокоточного решения трехмерных задач сейсмической разведки углеводородов и других полезных ископаемых. Разработанный гибридный метод позволяет одновременно описывать границы сложной формы за счет построения тетраэдральных сеток вблизи них и использования разрывного метода Галеркина, и экономить вычислительные ресурсы за счет применения сеточно-характеристического метода на структурированных регулярных сетках в остальной подобласти интегрирования. Также заметим, что предложенный в работе гибридный метод применим для моделирования волновых явлений в других объектах сложной формы.

Список литературы

Fang J., Chen H., Zhou H., Rao Y., Sun P., Zhang J. Elastic full-waveform inversion based on GPU accelerated temporal fourth-order finite-difference approximation. Computers & Geosciences. 2020. Т. 135. Номер статьи 104381. https://doi.org/10.1016/j.cageo.2019.104381
Решетова Г.В., Роменский Е.И. Моделирование волновых полей в пористых средах диффузно-интерфейсным подходом. Доклады Российской академии наук. Науки о Земле. 2021. Т. 497. № 2. С. 161–164. https://doi.org/10.31857/S2686739721040137
Takekawa J., Mikada H. A mesh-free finite-difference method for elastic wave propagation in the frequency-domain. Computers & Geosciences. 2018. T. 118. C. 65–78. https://doi.org/10.1016/j.cageo.2018.05.011
Liu J., Yong W. A., Liu J., Guo Z. Stable finite-difference methods for elastic wave modeling with characteristic boundary conditions. Mathematics. 2020. Т. 8. № 6. Номер статьи 1039. https://doi.org/10.3390/math8061039
Li Y., Brossier R., Métivier L. D frequency-domain elastic wave modeling with the spectral element method using a massively parallel direct solver. Geophysics. 2020. T. 85. № 2. C. T71–T88. https://doi.org/10.1190/GEO2019-0172.1
Ponomarenko R., Sabitov D., Charara M. Spectral element simulation of elastic wave propagation through fractures using linear slip model: microfracture detection for CO2 storage. 2020. Geophysical Journal International. T. 223. № 3. C. 1794–1804. https://doi.org/10.1093/gji/ggaa399
Duru K., Rannabauer L., Gabriel A. A., Igel H. A new discontinuous Galerkin method for elastic waves with physically motivated numerical fluxes. Journal of Scientific Computing. 2021. T. 88. № 3. C. 1–32. https://doi.org/10.1007/s10915-021-01565-1
Ладонкина М.Е., Неклюдова О.А., Остапенко В.В., Тишкин В.Ф. Комбинированная схема разрывного метода Галёркина, сохраняющая повышенную точность в областях влияния ударных волн. 2019. Доклады Академии наук. Т. 489. № 2. С. 119–124. https://doi.org/10.31857/S0869-56524892119-124
Khokhlov N., Favorskaya A., Stetsyuk V., Mitskovets I. Grid-characteristic method using Chimera meshes for simulation of elastic waves scattering on geological fractured zones. 2021. Journal of Computational Physics. Т. 446. Номер статьи 110637. https://doi.org/10.1016/j.jcp.2021.110637
Фаворская А.В., Петров И.Б. О численном моделировании пространственных динамических волновых эффектов в скальных массивах. Доклады Академии наук. 2017. Т. 474. № 4. С. 418–422. https://doi.org/10.7868/S0869565217040041
Gao L., Keyes D. Combining finite element and finite difference methods for isotropic elastic wave simulations in an energy-conserving manner. Journal of Computational Physics. 2019. T. 378. C. 665–685. https://doi.org/10.1016/j.jcp.2018.11.031
Lisitsa V., Tcheverda V., Botter C. Combination of the discontinuous Galerkin method with finite differences for simulation of seismic wave propagation. Journal of Computational Physics. 2016. T. 311. C. 142–157. https://doi.org/10.1016/j.jcp.2016.02.005
Петров И.Б., Фаворская А.В., Шевцов А.В., Васю-ков А.В., Потапов А.П., Ермаков А.С. О комбинированном методе для численного решения динамических пространственных упругопластических задач. Доклады Академии наук. 2015. Т. 460. № 4. С. 389. https://doi.org/10.7868/S0869565215040052
Favorskaya A., Petrov I. A novel method for investigation of acoustic and elastic wave phenomena using numerical experiments. Theoretical and Applied Mechanics Letters. 2020. T. 10. № 5. C. 307–314. https://doi.org/10.1016/j.taml.2020.01.040

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал