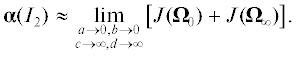Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 506, № 1, стр. 68-72

ОБ ОГРАНИЧЕННОСТИ И КОМПАКТНОСТИ ДВУМЕРНОГО ПРЯМОУГОЛЬНОГО ОПЕРАТОРА ХАРДИ

Член-корреспондент РАН В. Д. Степанов^1, *, Е. П. Ушакова^2, **

¹ Вычислительный Центр Дальневосточного отделения Российской академии наук
Хабаровск, Россия

² Институт проблем управления им. В.А. Трапезникова Российской академии наук
Москва, Россия

^* E-mail: stepanov@mi-ras.ru
^** E-mail: elenau@inbox.ru

Поступила в редакцию 13.05.2022
После доработки 12.08.2022
Принята к публикации 15.08.2022

EDN: WSKMID
DOI: 10.31857/S2686954322050162

Полный текст (PDF)

Аннотация

В терминах весовых функций $v$ и w на $\mathbb{R}_{ + }^{2}$ получены критерии ограниченности и компактности двумерного прямоугольного оператора интегрирования, действующего из весового пространства Лебега $L_{v}^{p}(\mathbb{R}_{ + }^{2})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{2})$, когда $1 < p,$ $q < \infty $. При $p < q$ критерий ограниченности значительно усиливает классический результат Е. Сойера (см. введение) для $p \leqslant q$. Случай $q < p$ также рассмотрен.

Ключевые слова: весовое пространство Лебега, неравенство Харди, двумерный прямоугольный оператор интегрирования, ограниченность, компактность

ВВЕДЕНИЕ

Пусть $n \in \mathbb{N}$. Для измеримых по Лебегу на $\mathbb{R}_{ + }^{n}: = (0,\infty {{)}^{n}}$ функций $f({{y}_{1}}, \ldots ,{{y}_{n}})$ n-мерный прямоугольный оператор интегрирования I_n задан формулой

(1)

$\begin{gathered} {{I}_{n}}f({{x}_{1}}, \ldots ,{{x}_{n}}): = \int\limits_0^{{{x}_{1}}} \ldots \int\limits_0^{{{x}_{n}}} f({{y}_{1}}, \ldots ,{{y}_{n}}){\kern 1pt} d{{y}_{1}} \ldots d{{y}_{n}} \\ ({{x}_{1}}, \ldots ,{{x}_{n}} > 0). \\ \end{gathered} $

Двойственное к I_n преобразование $I_{n}^{*}$ имеет вид

$\begin{gathered} I_{n}^{*}f({{x}_{1}}, \ldots ,{{x}_{n}}): = \int\limits_{{{x}_{1}}}^\infty \ldots \int\limits_{{{x}_{n}}}^\infty f({{y}_{1}}, \ldots ,{{y}_{n}}){\kern 1pt} d{{y}_{1}} \ldots d{{y}_{n}} \\ ({{x}_{1}}, \ldots ,{{x}_{n}} > 0). \\ \end{gathered} $

Пусть $1 < p,$ $q < \infty $ и $v,w \geqslant 0$ весовые функции на $\mathbb{R}_{ + }^{n}$. Весовое пространство Лебега $L_{v}^{p}(\mathbb{R}_{ + }^{n})$ состоит из всех измеримых на $\mathbb{R}_{ + }^{n}$ функций f таких, что ${\text{||}}f{\text{||}}_{{p,v}}^{p}: = \int\limits_{\mathbb{R}_{ + }^{n}} {\text{|}}f{{{\text{|}}}^{p}}v < \infty $. Далее будем иметь дело с интегральным неравенством Харди

(2)

${\text{||}}{{I}_{n}}f{\text{|}}{{{\text{|}}}_{{q,w}}} \leqslant {{C}_{n}}{\text{||}}f{\text{|}}{{{\text{|}}}_{{p,v}}}$

на конусе неотрицательных функций f из $L_{v}^{p}(\mathbb{R}_{ + }^{n})$. Константа ${{C}_{n}} > 0$ в (2) предполагается наименьшей из возможных и не зависит от f.

Задача характеризации неравенства (2) хорошо известна. Она равносильна нахождению критериев ограниченности I_n из $L_{v}^{p}(\mathbb{R}_{ + }^{n})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{n})$ и рассматривалась многими авторами (см. [1–4] и ссылки на литературу там же). Одномерный случай этого неравенства полностью изучен (см. [5–7]). Однако при $n > 1$ возникают трудности, препятствующие характеризации (2) без дополнительных ограничений на $v$ и w. Тем не менее хорошо известен результат Е. Сойера для произвольных $v$ и w в случае $1 < p \leqslant q < \infty $. Обозначим $p{\kern 1pt} ': = p$/(p – 1) и $\sigma : = {{v}^{{1 - p{\kern 1pt} '}}}$.

Теорема 1 [1, Theorem 1A]. Пусть $n = 2$ и $1 < p \leqslant q < \infty .$ Неравенство (2) выполнено для всех неотрицательных f на $\mathbb{R}_{ + }^{2}$ тогда и только тогда, когда одновременно выполнены три условия

(3)

$\begin{gathered} {{A}_{1}}: = \mathop {\sup }\limits_{(s,t) \in \mathbb{R}_{ + }^{2}} {{A}_{1}}[(s,t);\sigma ,w]: = \\ \,: = \mathop {\sup }\limits_{(s,t) \in \mathbb{R}_{ + }^{2}} {{[I_{2}^{*}w(s,t)]}^{{\frac{1}{q}}}}{{[{{I}_{2}}\sigma (s,t)]}^{{\frac{1}{{p{\kern 1pt} '}}}}} < \infty , \\ \end{gathered} $

(4)

$\begin{gathered} {{A}_{2}}: = \mathop {\sup }\limits_{(s,t) \in \mathbb{R}_{ + }^{2}} {{A}_{2}}[(s,t);\sigma ,w]: = \\ \,: = \mathop {\sup }\limits_{(s,t) \in \mathbb{R}_{ + }^{2}} {{\left( {\int\limits_0^s {\int\limits_0^t {{{{({{I}_{2}}\sigma )}}^{q}}w} } } \right)}^{{\frac{1}{q}}}}{{[{{I}_{2}}\sigma (s,t)]}^{{ - \frac{1}{p}}}} < \infty , \\ \end{gathered} $

(5)

$\begin{gathered} {{A}_{3}}: = \mathop {\sup }\limits_{(s,t) \in \mathbb{R}_{ + }^{2}} {{A}_{3}}[(s,t);\sigma ,w]: = \\ \,: = \mathop {\sup }\limits_{(s,t) \in \mathbb{R}_{ + }^{2}} {{\left( {\int\limits_s^\infty {\int\limits_t^\infty {{{{(I_{2}^{*}w)}}^{{p{\kern 1pt} '}}}\sigma } } } \right)}^{{\frac{1}{{p{\kern 1pt} '}}}}}{{[I_{2}^{*}w(s,t)]}^{{ - \frac{1}{{q{\kern 1pt} '}}}}} < \infty , \\ \end{gathered} $

причем ${{C}_{2}} \approx {{A}_{1}} + {{A}_{2}} + {{A}_{3}}$ с константами эквивалентности, зависящими только от параметров p и q.

Отметим, что в одномерном случае аналоги условий (3)–(5) эквивалентны друг другу [8]. При n = 2 это, вообще говоря, неверно. Более того, как показано в [1, § 4] для $p = q = 2$, никакие два условия из (3)–(5) не гарантируют выполнение (2). Однако конструкция второго контрпримера из [1, § 4] не переносится на случай $p < q.$

Цель настоящей работы – получить новые критерии выполнения неравенства Харди (2) при n = 2 и $1 < p \ne q < \infty $, а также исследовать компактность ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ для всех $p,q > 1$. Решение первой задачи содержится в теоремах 2 и 3 (см. ${{\S}}$ 1). В теореме 4 найдены альтернативные достаточные условия на $v$ и w для выполнения (2) в случае $n = 2$ и $1 < q < p < \infty $. Напомним, что критерий Е. Сойера ограниченности I₂ из $L_{v}^{p}(\mathbb{R}_{ + }^{2})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{2})$ при $1 < p \leqslant q < \infty $ выражается конечностью трех независимых функционалов (см. теорему 1). В теореме 2 показано, что при $p < q$ неравенство (2) характеризуется конечностью только одного функционала. С некоторым ограничением на $v$ и w аналогичное утверждение получено и для $q < p$ (см. теорему 3). В ${{\S}}$ 2 представлены условия компактности оператора I₂ из $L_{v}^{p}(\mathbb{R}_{ + }^{2})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{2})$, а также характеризуется мера некомпактности ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ в случае $1 < p \leqslant q < \infty $.

Аналоги теорем 2 и 3 также справедливы для двойственного оператора $I_{2}^{*}$ и смешанных операторов Харди, относительно деталей см. [1, Remark 1].

Билинейные весовые неравенства с прямоугольными операторами интегрирования изучены в [9]. Также некоторые аспекты многомерных неравенств рассматривались в работах [10–13].

На протяжении всей работы запись вида $\Phi \lesssim \Psi $ означает $\Phi \leqslant c\Psi $ с некоторой константой $c > 0$, зависящей только от параметров суммирования p и q. Мы пишем $\Phi \approx \Psi $ в случае $\Phi \lesssim \Psi \lesssim \Phi $. Символ ${{\chi }_{E}}$ обозначает характеристическую функцию множества $E.$ Значки $: = $ и $ = :$ применяются для определения новых величин.

1. УСЛОВИЯ ОГРАНИЧЕННОСТИ

Обозначим

$\alpha (p,q): = \frac{{{{p}^{2}}(q - 1)}}{{q - p}},\quad p < q;$

$\begin{gathered} \beta (p,q,c): = 3\max \left\{ {\frac{{{{3}^{{3q + 1}}}}}{4},\,\,\frac{{{{3}^{{\frac{q}{p} + 2q}}}}}{{{{2}^{{\frac{q}{p}}}}}},} \right. \\ \left. {\frac{{{{3}^{{2q - \frac{q}{p} + 2 - c}}}}}{{4c}}\left[ {\frac{{2 \cdot {{3}^{{3c}}}}}{{1 - c}} - {{3}^{{c - 2}}}} \right]} \right\},\quad q < p, \\ \end{gathered} $

где $1{\text{/}}r: = 1{\text{/}}q - 1{\text{/}}p$ и $0 < q{\text{/}}p \leqslant c < 1$. Положим $\sigma : = {{v}^{{1 - p'}}}$ и

$\begin{gathered} B: = {{\left( {\int\limits_{\mathbb{R}_{ + }^{2}} {{d}_{y}}{{{[{{I}_{2}}\sigma (x,y)]}}^{{\frac{r}{{p{\kern 1pt} '}}}}}{\kern 1pt} {{d}_{x}}( - {{{[I_{2}^{*}w(x,y)]}}^{{\frac{r}{q}}}})} \right)}^{{\frac{1}{r}}}} = \\ \, = {{\left( {\int\limits_{\mathbb{R}_{ + }^{2}} {{{[{{I}_{2}}\sigma (x,y)]}}^{{\frac{r}{{p{\kern 1pt} '}}}}}{\kern 1pt} {{d}_{x}}{\kern 1pt} {{d}_{y}}{{{[I_{2}^{ * }w(x,y)]}}^{{\frac{r}{q}}}}} \right)}^{{\frac{1}{r}}}} = \\ \, = {{\left( {\int\limits_{\mathbb{R}_{ + }^{2}} {{{[I_{2}^{*}w(x,y)]}}^{{\frac{r}{q}}}}{\kern 1pt} {{d}_{x}}{\kern 1pt} {{d}_{y}}{{{[{{I}_{2}}\sigma (x,y)]}}^{{\frac{r}{{p{\kern 1pt} '}}}}}} \right)}^{{\frac{1}{r}}}}, \\ \end{gathered} $

где последние два равенства получаются интегрированием по частям.

Введем обозначения

$\begin{gathered} {{\mathbb{C}}_{{t,s}}}{{: = 3}^{{3q}}}\left[ {4{{{\left( {\frac{2}{3}} \right)}}^{q}}\max \left\{ {t,2q{{{(q{\kern 1pt} ')}}^{{\frac{q}{{p{\kern 1pt} '}}}}}} \right\}{{{\left( {\frac{{{{2}^{{p - 1}}}}}{{{{2}^{{p - 1}}} - 1}}} \right)}}^{{\frac{q}{p}}}}} \right. + \\ \, + \left. {{{3}^{{\frac{1}{p}}}}{{s}^{{\frac{1}{{p{\kern 1pt} '}}}}}{{{\left( {\frac{{{{3}^{{q - 1}}}}}{{{{3}^{{q - 1}}} - 1}}} \right)}}^{{\frac{1}{{q{\kern 1pt} '}}}}}} \right], \\ \end{gathered} $

$\begin{gathered} {{{\mathbf{C}}}_{{t,s}}}{{: = 3}^{{3q}}}\left[ {{{2}^{q}}{{3}^{{ - q}}}\max \left\{ {t,2q{{{(p{\kern 1pt} ')}}^{{q - 1}}}{{{\left( {\frac{q}{r}} \right)}}^{{\frac{q}{r}}}}} \right\}{{{\left( {\frac{{{{2}^{{p - 1}}}}}{{{{2}^{{p - 1}}} - 1}}} \right)}}^{{\frac{q}{p}}}}} \right. + \\ \, + \left. {3{\kern 1pt} {{s}^{{\frac{1}{{p{\kern 1pt} '}}}}}{{{\left( {\frac{{{{3}^{{q - 1}}}}}{{{{3}^{{q - 1}}} - 1}}} \right)}}^{{\frac{1}{{q{\kern 1pt} '}}}}}} \right]. \\ \end{gathered} $

Усилением теоремы 1 для $p < q$ является следующее утверждение.

Теорема 2 [14]. Пусть $1 < p < q < \infty $. Неравенство

(6)

${{\left( {\int\limits_{\mathbb{R}_{ + }^{2}} {{{({{I}_{2}}f)}}^{q}}w} \right)}^{{\frac{1}{q}}}} \leqslant {{C}_{2}}{{\left( {\int\limits_{\mathbb{R}_{ + }^{2}} {{f}^{p}}v} \right)}^{{\frac{1}{p}}}}$

выполнено тогда и только тогда, когда ${{A}_{1}} < \infty $, при этом

${{A}_{1}} \leqslant {{C}_{2}} \leqslant {{\mathbb{C}}_{{\alpha ,\alpha {\kern 1pt} *}}}{\kern 1pt} {{A}_{1}},$

где $\alpha : = \alpha (p,q)$ и $\alpha {\kern 1pt} *: = \alpha (q{\kern 1pt} ',p{\kern 1pt} ')$.

Напомним, что в случае $p \leqslant q$ наилучшая константа C₂ двумерного неравенства (6) эквивалентна $\sum\nolimits_{i = 1}^3 {{A}_{i}}$ (см. теорему 1). Однако для $p < q$ имеют место неравенства

(7)

$\begin{gathered} {{A}_{1}} \leqslant {{C}_{2}} \leqslant {{\mathbb{C}}_{{1,1}}}[{{A}_{1}} + {{A}_{2}} + {{A}_{3}}] \leqslant \\ \, \leqslant {{\mathbb{C}}_{{1,1}}}[1 + \alpha {{(p,q)}^{{\frac{1}{q}}}} + \alpha {{(q{\kern 1pt} ',p{\kern 1pt} ')}^{{\frac{1}{{p{\kern 1pt} '}}}}}]{{A}_{1}}. \\ \end{gathered} $

При этом ${{\lim }_{{p \to q - 0}}}[\alpha (p,q) + \alpha (q{\kern 1pt} ',p{\kern 1pt} ')] = \infty $. Таким образом, правое неравенство в (7) и оценка сверху в теореме 2 при $p \to q - 0$ имеют blow-up эффект.

Новый результат в случае $q < p$ формулирует следующее утверждение.

Теорема 3. Пусть $1 < q < p < \infty $. Предположим, что весовая функция ${v}$ удовлетворяет условию:

(8)

$\begin{gathered} существует\;\gamma \in [q{\text{/}}p,1) \\ такое,{\text{ }}что\;\frac{{{{\partial }^{2}}([{{I}_{2}}\sigma (x,y{{{)]}}^{\gamma }})}}{{\partial x\partial y}} \geqslant 0 \\ для{\text{ }}п.в.\;(x,y) \in \mathbb{R}_{ + }^{2}. \\ \end{gathered} $

Кроме этого, для веса w выполнено условие:

(9)

$\begin{gathered} существует\;\gamma {\kern 1pt} * \in [p{\kern 1pt} '{\text{/}}q{\kern 1pt} ',1) \\ такое,что\;\frac{{{{\partial }^{2}}([I_{2}^{*}w(x,y{{{)]}}^{{\gamma {\kern 1pt} *}}})}}{{\partial x\partial y}} \geqslant 0 \\ для\;п.в.\;(x,y) \in \mathbb{R}_{ + }^{2}. \\ \end{gathered} $

Тогда неравенство (6) выполнено тогда и только тогда, когда $B < \infty $, при этом

(10)

${{2}^{{ - \frac{1}{{p{\kern 1pt} '}}}}}{{\left( {\frac{q}{r}} \right)}^{{\frac{1}{q}}}}{{\left( {\frac{{p{\kern 1pt} '}}{r}} \right)}^{{\frac{1}{{p{\kern 1pt} '}}}}}B \leqslant {{C}_{2}} \leqslant {{{\mathbf{C}}}_{{\beta ,\beta {\kern 1pt} *}}}{\kern 1pt} B,$

где $\beta : = \beta (p,q,\gamma )$ и $\beta {\kern 1pt} *: = \beta (q{\kern 1pt} ',p{\kern 1pt} ',\gamma {\kern 1pt} *)$.

Замечание 1. Оценка снизу в (10) справедлива без требований (8) и (9) на весовые функции $v$ и w. В качестве весов, удовлетворяющих (8) и (9), подходят, к примеру, $\sigma (x,y) = (x + y{{)}^{\tau }}$, $\tau > 0$, и w(x, y) = ${{(x + y)}^{{ - \rho }}}$, $\rho > 2$.

В завершение параграфа представим альтернативные достаточные условия выполнения неравенства (6) без дополнительных ограничений на $v$ и w.

Теорема 4. Пусть $1 < q < p < \infty $. Неравенство (6) выполнено, если

(11)

${{B}_{v}}: = {{\left( {\int\limits_{\mathbb{R}_{ + }^{2}} \sigma (u,z){{{\left( {\int\limits_u^\infty \int\limits_z^\infty {{{({{I}_{2}}\sigma )}}^{{q - 1}}}w} \right)}}^{{\frac{r}{q}}}}{\kern 1pt} du{\kern 1pt} dz} \right)}^{{\frac{1}{r}}}} < \infty ,$

причем ${{C}_{2}} \lesssim {{B}_{v}}$.

Верна также двойственная формулировка последней теоремы с функционалом

${{B}_{w}}: = {{\left( {\int\limits_{\mathbb{R}_{ + }^{2}} w(u,z){{{\left( {\int\limits_0^u \int\limits_0^z {{{(I_{2}^{*}w)}}^{{p{\kern 1pt} ' - 1}}}\sigma } \right)}}^{{\frac{r}{{p{\kern 1pt} '}}}}}{\kern 1pt} du{\kern 1pt} dz} \right)}^{{\frac{1}{r}}}}$

вместо ${{B}_{v}}$.

Замечание 2. Если веса $v$ и w факторизуемы, т.е. представляются в виде произведения одномерных функций, то условие ${{B}_{v}} < \infty $ (или ${{B}_{w}} < \infty $) необходимо и достаточно для выполнения (6) в случае $1 < q < p < \infty $, при этом ${{C}_{2}} \approx {{B}_{v}} \approx {{B}_{w}}$ [4].

2. КОМПАКТНОСТЬ И МЕРА НЕКОМПАКТНОСТИ

Предположим, что $1 < p,$ $q < \infty $ и оператор I₂ ограничен из $L_{v}^{p}(\mathbb{R}_{ + }^{2})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{2})$.

Пусть $a,b,c,d \in (0,\infty )$ такие, что $a < c$ и $b < d$. Обозначим

${{\Omega }_{0}}: = {{\Omega }_{0}}(a,b): = \{ (0,a) \times (0,\infty )\} \cup \{ [a,\infty ) \times (0,b)\} ,$

$\begin{gathered} {{\Omega }_{\infty }}: = {{\Omega }_{\infty }}(a,b,c,d): = \\ \,: = \{ [a,\infty ) \times (d,\infty )\} \cup \{ (c,\infty ) \times [b,d]\} . \\ \end{gathered} $

Для формулировки критерия компактности ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ в случае $p \leqslant q$ нам понадобятся следующие условия:

(12)

$\begin{gathered} \mathop {\lim }\limits_{\substack{ a \to 0,{\kern 1pt} b \to 0 \\ c \to \infty ,{\kern 1pt} d \to \infty } } \left[ {\mathop {\sup }\limits_{(u,z) \in {{\Omega }_{0}}} {{A}_{1}}[(u,z);\sigma ,w] + } \right. \\ \, + \left. {\mathop {\sup }\limits_{(u,z) \in {{\Omega }_{\infty }}} {{A}_{1}}[(u,z);\sigma ,w]} \right] = 0, \\ \end{gathered} $

(13)

$\begin{gathered} \mathop {\lim }\limits_{\substack{ a \to 0,{\kern 1pt} b \to 0 \\ c \to \infty ,{\kern 1pt} d \to \infty } } \left[ {\mathop {\sup }\limits_{(u,z) \in {{\Omega }_{0}}} {{A}_{2}}[(u,z);\sigma ,w] + } \right. \\ \, + \left. {\mathop {\sup }\limits_{(u,z) \in {{\Omega }_{\infty }}} {{A}_{2}}[(u,z);\sigma {{\chi }_{{{{\Omega }_{\infty }}}}},w{{\chi }_{{{{\Omega }_{\infty }}}}}]} \right] = 0, \\ \end{gathered} $

(14)

$\begin{gathered} \mathop {\lim }\limits_{\substack{ a \to 0,{\kern 1pt} b \to 0 \\ c \to \infty ,{\kern 1pt} d \to \infty } } \left[ {\mathop {\sup }\limits_{(u,z) \in {{\Omega }_{0}}} {{A}_{3}}[(u,z);\sigma {{\chi }_{{{{\Omega }_{0}}}}},w{{\chi }_{{{{\Omega }_{0}}}}}] + } \right. \\ \, + \left. {\mathop {\sup }\limits_{(u,z) \in {{\Omega }_{\infty }}} {{A}_{3}}[(u,z);\sigma ,w]} \right] = 0. \\ \end{gathered} $

Теорема 5. Пусть $1 < p \leqslant q < \infty $. Если p < q, то ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ компактен тогда и только тогда, когда ${{A}_{1}} < \infty $ и выполнено (12).

В случае p = q оператор ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{p}(\mathbb{R}_{ + }^{2})$ компактен, если и только если $\sum\nolimits_{i = 1,2,3} {{A}_{i}} < \infty $ и выполнены условия (12)–(14).

Для q < p достаточное условие и необходимое условие компактности ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ представлены в следующей теореме.

Теорема 6. Пусть $1 < q < p < \infty $. Оператор ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ компактен, если выполнено (11). Если ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ компактен, то $B < \infty $.

Замечание 3. С условиями (8) и (9) на весовые функции $v$ и $w$, соответственно, оператор ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ компактен, если и только если $B < \infty $.

Далее, определим

$\alpha (T): = \inf {\text{||}}T - P{\text{||}},$

где инфимум берется по всем ограниченным линейным отображениям $P:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ конечного ранга. Величина $\alpha (T)$ совпадает с так называемым множеством меры некомпактности оператора T, действующего ограниченно из $L_{v}^{p}(\mathbb{R}_{ + }^{2})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{2})$ (см. [15, § 2] и [16, Proposition 3.1]).

Так как для $1 < q < p$ оператор I₂ из $L_{v}^{p}(\mathbb{R}_{ + }^{2})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{2})$ компактен тогда и только тогда, когда он ограничен (см. [17, 18, § 5.3]), то в таком случае $\alpha ({{I}_{2}}) = 0$. Это следует из аппроксимационного свойства пространства $L_{w}^{q}(\mathbb{R}_{ + }^{2})$ [19, § 10.2.3/1]. Для пространств Y, обладающих таким свойством, известно, что $\alpha (T) = 0$ тогда и только тогда, когда $T:X \to Y$ компактен [19, § 10.1.3].

Рассмотрим ситуацию, когда $1 < p \leqslant q < \infty $. Положим

$\begin{gathered} {{A}_{1}}({{\Omega }_{0}}): = \mathop {\sup }\limits_{(u,z) \in {{\Omega }_{0}}} {{A}_{1}}[(u,z);\sigma ,w], \\ {{A}_{1}}({{\Omega }_{\infty }}): = \mathop {\sup }\limits_{(u,z) \in {{\Omega }_{\infty }}} {{A}_{1}}[(u,z);\sigma ,w]; \\ \end{gathered} $

$\begin{gathered} {{A}_{2}}({{\Omega }_{0}}): = \mathop {\sup }\limits_{(u,z) \in {{\Omega }_{0}}} {{A}_{2}}[(u,z);\sigma ,w], \\ {{A}_{2}}({{\Omega }_{\infty }}): = \mathop {\sup }\limits_{(u,z) \in {{\Omega }_{\infty }}} {{A}_{2}}[(u,z);\sigma {{\chi }_{{{{\Omega }_{\infty }}}}},w{{\chi }_{{{{\Omega }_{\infty }}}}}]; \\ \end{gathered} $

$\begin{gathered} {{A}_{3}}({{\Omega }_{0}}): = \mathop {\sup }\limits_{(u,z) \in {{\Omega }_{0}}} {{A}_{3}}[(u,z);\sigma {{\chi }_{{{{\Omega }_{0}}}}},w{{\chi }_{{{{\Omega }_{0}}}}}], \\ {{A}_{3}}({{\Omega }_{\infty }}): = \mathop {\sup }\limits_{(u,z) \in {{\Omega }_{\infty }}} {{A}_{3}}[(u,z);\sigma ,w]. \\ \end{gathered} $

Пусть

(15)

$J({{\Omega }_{0}}): = {{A}_{1}}({{\Omega }_{0}})\quad {\text{и}}\quad J({{\Omega }_{\infty }}): = {{A}_{1}}({{\Omega }_{\infty }})$

в случае $1 < p < q < \infty $; для p = q мы полагаем

(16)

$J({{\Omega }_{0}}): = \sum\limits_{i = 1}^3 {{A}_{i}}({{\Omega }_{0}})\quad {\text{и}}\quad J({{\Omega }_{\infty }}): = \sum\limits_{i = 1}^3 {{A}_{i}}({{\Omega }_{\infty }}).$

Для $1 < p \leqslant q < \infty $ мера некомпактности ${{I}_{2}}:L_{v}^{p}(\mathbb{R}_{ + }^{2}) \to L_{w}^{q}(\mathbb{R}_{ + }^{2})$ охарактеризована в следующем утверждении.

Теорема 7. Пусть $1 < p \leqslant q < \infty $ и I₂ограничен из $L_{v}^{p}(\mathbb{R}_{ + }^{2})$ в $L_{w}^{q}(\mathbb{R}_{ + }^{2})$. Тогда

Список литературы

Sawyer E. Weighted inequalities for two-dimensional Hardy operator // Studia Math. 1985. V. 82. № 1. P. 1–16.
Kokilashvili V., Meskhi A., Persson L.-E. Weighted norm inequalities for integral transforms with product kernels // New-York: Nova Science Publishers, 2009. 342 pp.
Meskhi A. A note on two-weight inequalities for multiple Hardy-type operators // J. Funct. Spaces Appl. 2005. V. 3. № 3. P. 223–237.
Persson L.-E., Ushakova E.P. Some multi-dimensional Hardy type integral inequalities // J. Math. Inequal. 2007. V. 1. № 3. 301–319.
Bradley J.S. Hardy inequalities with mixed norms // Canad. Math. Bull. 1978. V. 21. № 4. P. 405–408.
Прохоров В.Д., Степанов В.Д., Ушакова Е.П. Интегральные операторы Харди-Стеклова // Совр. пробл. матем. 2016. Т. 22. 186 с.
Sinnamon G., Stepanov V.D. The weighted Hardy inequality: new proofs and the case p = 1 // J. London Math. Soc. 1992. V. 2. № 2. P. 232–242.
Gogatishvili A., Kufner A., Persson L.-E., Wedestig A. An equivalence theorem for integral conditions related to Hardy’s inequality // Real Anal. Exchange. 2003/04. V. 29. № 2. P. 867–880.
Степанов В.Д., Шамбилова Г.Э. О двумерных билинейных неравенствах с прямоугольными операторами Харди в весовых пространствах Лебега // Труды МИАН. 2021. Т. 312. С. 251–258.
Wedestig A. Weighted inequalities for the Sawyer two-dimensional Hardy operator and its limiting geometric mean operator // J. Inequal. Appl. 2005. V. 4. P. 387–394.
Barza S., Kamińska A., Persson L.-E., Soria J. Mixed norm and multidimensional Lorentz spaces // Positivity. 2006. V. 10. № 3. P. 539–554.
Forzani L., Martń-Reyes F.J., Ombrosi S. Weighted inequalities for the two-dimensional one-sided Hardy–Littlewood maximal function // Trans. Amer. Math. Soc. 2011. V. 363. № 4. P. 1699–1719.
Kumar S. A Hardy-type inequality in two dimensions // Indag. Math. (N.S.) 2009. V. 20. № 2. P. 247–260.
Stepanov V.D., Ushakova E.P. On weighted Hardy inequality with two-dimensional rectangular operator – extension of the E. Saywer theorem // Math. Ineq. & Appl. 2021. V. 24. № 3. P. 617–634.
Edmunds D.E., Stepanov V.D. The measure of non–compactness and approximation numbers of certain Volterra integral operators // Math. Ann. 1994. V. 298. P. 41–66.
Canavati J.A., Galaz-Fontes F. Compactness of imbeddings between Banach spaces and applications to Sobolev spaces // J. Lond. Math. Soc., II Ser. 1990. V. 41. № 2. P. 511–525.
Ando T. On compactness of integral operators // Indag. Math. (New Series). 1962. V. 24. P. 235–239.
Красносельский М.А., Забрейко П.П., Пустыльник Е.И., Соболевский П.Е. Интегральные операторы в пространствах суммируемых функций // М.: Наука, 1966. 500 с.
Пич А. Операторные идеалы. М.: Мир, 1982. 536 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал