Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 508, № 1, стр. 79-87

1. ВВЕДЕНИЕ

Высокие темпы индустриализации в современном мире способствуют повышению объемов перевозок. Данная проблема особенно остро стоит в области железнодорожных перевозок, т.к. изменение ее инфраструктуры достаточно трудозатратно и возникает задача оптимального использования уже имеющихся ресурсов. Увеличивается плотность перевозок как в грузовом, так и в пассажирском движениях. Вследствие этого повышаются требования к исполнению запланированного плана движения, и любое отклонение от него может привести к значительным неустойкам, например, увеличению задержки поездов, их отмене [1]. Поэтому разработка систем управления для данной области является актуальным и перспективным направлением. В данной сфере существуют высокие требования к безопасности движения, которые приводят к дополнительным трудностям и ограничениям. Вследствие этого задача эффективного управления железнодорожным трафиком становится крайне сложной. С данной проблемой сталкиваются все транспортные и логистические компании по всему миру.

Одними из тех, кто задался целью создать в этой области наиболее эффективное решение, которое будет основано на применении новейших подходов, в том числе и искусственного интеллекта, стали Швейцарские федеральные железные дороги и Deutsche Bahn AG. Для этой цели они организовали соревнования Flatland на платформе AICrowd. В данном соревновании участникам предоставляется симулятор, моделирующий процессы движения поездов и работу железнодорожной инфраструктуры, для проведения экспериментов по апробации реализованных алгоритмов. В данном соревновании есть два трека – один для решений, основанных на использовании классических алгоритмов, другой – основанных на использовании мультиагентного обучения с подкреплением [1].

В третьей версии симулятора, предназначенного для Flatland версии 3 (конкурс 2019 г.) был добавлен функционал, который также проверяет пунктуальность и точность следования заданному графику [2]. Для каждого поезда существует заданное расписание с конкретными временами прибытия и отправления на станциях, а также окно времени, в течение которого они должны стартовать и добраться до места назначения. Расписание составлено таким образом, чтобы у каждого поезда было больше времени, чем теоретически необходимо, для прибытия в пункт назначения. Поэтому необходимо использовать этот запас времени таким образом, чтобы все поезда прибывали с минимальной задержкой, например, пропуская другие поезда или уступая дорогу.

Цель соревнования состоит в том, чтобы реализовать алгоритм построения расписания движения поездов, в котором все поезда прибудут в пункт назначения с минимальной задержкой по отношению к требуемому времени прибытия.

Проблема построения эффективных расписаний является одной из самых сложных проблем в области планирования и управления железнодорожным транспортом. При ее решении необходимо учитывать различные аспекты организации перевозочного процесса [3]. Эта задача может быть сформулирована как классическая задача исследования операций (operation research; OR) и как задача обучения с подкреплением. Решение, представленное в данной статье, было предложено для участия в конкурсе Flatland 3 в треке Reinforcement Learning, где заняло первое место [4].

Поиск решения в данной области связан с проблемой принятия решений при появлении других агентов на пути, стохастического характера поломок и реакцией на разреженную функцию вознаграждения, заданную в симуляторе. Данная проблема связана с особенностями мультиагентного обучения и основным инструментом ее решения является использование методов обучения с подкреплением с централизованным критиком [5]. Однако введенная новая концепция расписаний создает особые трудности при обучении и придает чувствительность конструированию функции вознаграждения. В связи с этим реализованный подход основан на технике структурирования вознаграждения, а также специально разработанной стратегии обучения по расписанию. Распространенный способ адаптации к новым особенностям задачи заключается в преобразовании новых знаний предметной области в дополнительные вознаграждения и обучении агентов с помощью комбинации оригинальных и новых вознаграждений [6, 7]. В данном случае была разработана дополнительная компонента, отражавшая степень отставания поезда от его расписания.

Результаты показали, что разработанная стратегия обучения по расписанию способна вовремя справляться с каждым уровнем сложности, что дало возможность обучить модель в более сложных средах. Предложенная гибридная структура вознаграждения отвечала новым аспектам задачи и позволила эффективно преодолеть трудности нового издания конкурса Flatland 3.

2. ОСОБЕННОСТИ СИМУЛЯТОРА

Рассмотрим особенности среды Flatland 3 для управления в сфере транспортных коммуникаций [8].

Среда

Flatland – это симулятор, моделирующий динамику движения поездов, а также железнодорожную инфраструктуру. Данный симулятор генерирует уровни, которые представляют собой двумерную сетку, где каждая клетка имеет свой тип: поворот, дорога, развилка или недоступная местность. Каждый поезд занимает одну клетку на сетке и имеет цель и направление. Как и в реальных железнодорожных сетях поезда не движутся с одинаковой скоростью, а имеют разную заданную скорость передвижения в соответствии с типом поезда. Например, грузовой поезд будет двигаться медленнее, чем пассажирский поезд и в связи с этим необходимо избегать планирования быстрого поезда за медленным. Также каждый поезд имеет свое временное окно, в течение которого он должен стартовать и прибыть в пункт назначения. В случае столкновения поездов возникает пробка.

Наблюдения

Со стороны агента Flatland предоставляет доступ практически ко всей информации о текущем состоянии среды, на основе которой можно построить свой вид наблюдений. В симуляторе уже реализованы 3 вида наблюдений [8]:

– глобальное наблюдение – самое простое. В этом случае каждому агенту предоставляется глобальный обзор всей среды;

– наблюдение по локальной сетке – похоже на глобальное, однако размеры наблюдаемого окружения ограничены;

– “Tree observation” – основано на том факте, что сеть железных дорог является графом, и поэтому наблюдение строится только вдоль разрешенных переходов в графе. Наблюдение создается путем охвата 4-х разветвленного дерева от текущей позиции агента. Каждая ветвь следует разрешенным переходам (обратная ветвь разрешена только в тупиках) до тех пор, пока не будет достигнута ячейка с несколькими разрешенными переходами. Здесь информация, собранная по ветке, сохраняется в виде узла в дереве.

Действия

Симуляция происходит пошагово. Каждый агент поезда на каждом шаге должен определить, какое действие ему совершить. Поезда во Flatland имеют весьма ограниченный набор действий, как и следовало ожидать от симулятора железной дороги. Это означает, что допустимы только несколько действий, а именно: повернуть налево, повернуть направо, двигаться вперед, продолжать предыдущее действие или остановиться.

К этому стоит добавить то, что с заданной частотой симулятор имитирует поломки. Непредвиденные события часто встречаются на железнодорожных сетях. Первоначальный план необходимо перепланировать в реальном времени, поскольку незначительные события, такие как задержка отправления с железнодорожных станций, поломки поездов или инфраструктуры, или даже проблемы с погодой, приводят к опозданию поездов. Механизм возникновения поломок реализован с использованием процесса Пуассона, а именно задержка имитируется путем остановки агентов в случайное время на случайные промежутки времени. Поезд с такой неисправностью не может двигаться в течение некоторого количества шагов симуляции, в результате чего он блокирует следующие за ними поезда, что часто приводит к пробкам.

Метрика поведения агента

Во Flatland 3 отклик вознаграждения предусматривается только в конце эпизода, что делает заданную по умолчанию функцию вознаграждения разреженной. Решения оцениваются по суммарному отклонению поездов от графика.

Эпизод заканчивается, когда все поезда достигают своей цели или при достижении максимального количества временных шагов. В конце эпизода для каждого поезда могут быть следующие варианты:

1. Поезд приехал в пункт назначения:

o 0 – если приехал вовремя или раньше;

o –min(${{t}_{l}}$ – ${{t}_{a}}$, 0) – если опоздал, где ${{t}_{l}}$ указывает шаг моделирования до или на котором ожидается, что агент достигнет пункта назначения, а ${{t}_{a}}$ – реальное время прибытия агента.

2. Поезд не достиг своей цели. Если поезд вообще не прибывает к месту назначения, то в соответствии с общими принципами работы железных дорог учитываются дополнительные штрафы. Тогда вознаграждение отрицательное и пропорционально опозданию поезда, а также расчетному количеству времени, необходимому для достижения цели агента с его текущей позиции по кратчайшему пути (${{t}_{{sp}}}$):

3. Поезд так и не тронулся. В данном случае поезд считается отмененным, и предоставляется следующее вознаграждение:

(–1)* cancellation_factor * (${{t}_{{sp}}}$ + cancellation_time_buffer),

где cancellation_factor и cancellation_time_buffer – специальные параметры, настраиваемые организаторами конкурса.

Данная структура вознаграждения создает особые трудности при обучении. Рассмотрим их и методы их преодоления подробнее.

3. ЗАДАЧА И ЕЕ ОСОБЕННОСТИ

Задача соревнования состоит в наборе максимального количества очков по двум критериям. Во-первых, основываясь на суммарной функции вознаграждения, набранной всеми агентами. Во-вторых, показав наилучший процент агентов, благополучно доехавших до станции назначения. При этом оценка решения устроена так, что с каждым успешно завешенным уровнем структура следующего уровня железнодорожной сети усложняется и число поездов увеличивается, поэтому агентам приходится решать задачи все большего масштаба. С каждым раундом сложность первоначальной среды также увеличивался, а кроме этого, добавляется новое дополнительное требование, например, скоростной режим. И главная задача третьего издания конкурса состоит в том, чтобы составить наилучшее расписание, при котором все поезда прибывают в пункт назначения с минимальной задержкой.

Задачу также усложняют непредсказуемые задержки при сбоях в работе поездов. Поломки заставляют агентов оперативно изменять свои планы, что может привести к негативным последствиям, что в свою очередь отражается на сложности обучения модели RL.

Рассмотрим последствия, к которым приводят упомянутые трудности задачи.

Основной проблемой являются пробки – плохо обученная модель не справляется с многоагентной маршрутизацией поездов. Однако и более успешные модели могут не решить проблему пробок из-за сопутствующих факторов, например, поломки или большого количества одновременно стартующих поездов.

Другой проблемой является тенденция скорых поездов следовать за более медленными по удобной им дороге, ухудшая таким образом оптимальность конечного решения.

Наконец, самой глобальной и сложной проблемой оказалась уже упомянутая структура функции вознаграждения, которая во многих аспектах мешала обучению. Она могла привести, например, к потере ориентира, проезда мимо цели или намеренному попаданию в пробку.

Рассмотрим предложенную модель решения поставленной задачи и ее сопутствующих.

4. АРХИТЕКТУРА МОДЕЛИ

Базовая архитектура предложенной модели представляет собой полносвязную сеть с обучением по типу Proximal Policy Optimization (PPO) [9]. В режиме выполнения это обеспечивает быстроту принятия решения агентом. При этом во время обучения в дополнение к первой используется другая, более сложная сеть, которая дает свой вклад в градиенты для обучения сети агента. Этому агенту, называемому “центральным критиком”, предоставляется более целостное представление о состоянии среды, с помощью которого он аппроксимирует адекватный отклик на то или иное действие агента в текущей ситуации.

Существует множество вариаций метода централизованного критика [5, 10, 11]. Реализованный вариант не использует глобальные наблюдения, но объединяет наблюдения обучаемого агента с наблюдениями других агентов. Такой подход был выбран для того, чтобы создать решение, легко расширяемое для масштабных сред. Еще одним дополнением в мультиагентный алгоритм PPO с централизованным критиком является то, что в архитектуру критика добавлен трансформер, который позволяет критику эффективно объединять представления своих и чужих наблюдений [12]. Это позволяет работать с разреженными наблюдениями и неоднородностью данных, а также с возможной инвариантностью перестановок в случае изменения подмножества агентов, включенных в наблюдение [8].

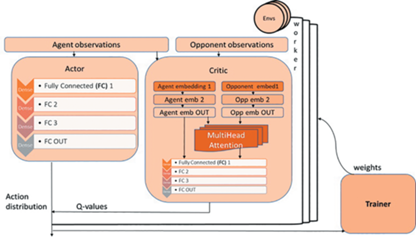
На рис. 1 представлена архитектура модели, состоящей из Актора, который прогнозирует политику агента, т.е. вероятностное распределение действий в данном состоянии, и Критика, который выдает аппроксимацию вознаграждения среды на то или иное действие агента (Q-value). Далее модель обучается, чтобы улучшить выгоду (Advantage) от данного действия. Для обеспечения устойчивости модели использовалось сразу несколько параллельных потоков, которые одновременно собирали опыт для объекта Trainer’а, при этом каждый взаимодействовал сразу с несколькими средами.

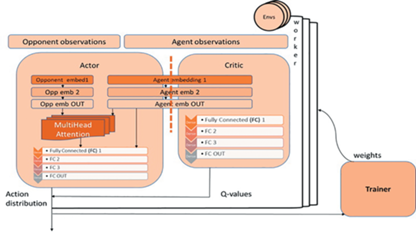
В ходе экспериментов была также реализована альтернативная модель с трансформатором, перемещенным в Aктора. Здесь основное наполнение было помещено в Aктора. Он получал информацию о наблюдениях ближайших соседей агента и, преобразуя их в векторные представления (embeddings) вместе с собственными представлениями агента передавал в слой Multi Head Attention. Cлой представлений агента был сконструирован таким образом, что его можно было сделать как разделенным для Критика и Актора, так и общим.

К сожалению, для настройки данной модели не было достаточно времени, поэтому она дала более слабые результаты и не была использована в окончательном решении. К тому же такой нагруженный Актор в режиме выполнения может достаточно долго проводить вычисления. В дальнейшем планируется исследование потенциала данной альтернативной архитектуры модели.

5. ОБЩАЯ СТРАТЕГИЯ РЕШЕНИЯ

Разработанные наблюдения

Для более результативного использования информации, получаемой от окружающей среды, предложенная симулятором система наблюдений “Tree observation” [8] была модифицирована. Основным нововведением стал учет особенностей работы с расписаниями движения поездов. Информация, хранящаяся в узле, была расширена – помимо основной информации о маршруте поезда, его скорости, инфраструктуре сети и других поездах, встречающихся на пути, была добавлена информация о временном отклонении от графика, сравнение индекса с другими поездами на пути, а также о потенциальных конфликтах на рассматриваемой ветке движения.

Структурирование вознаграждений

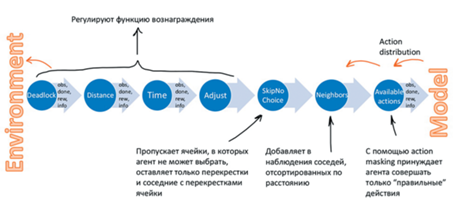
Для повышения эффективности разработанного алгоритма, а также для борьбы с описанными выше трудностями был изменен процесс взаимодействия агента с симулятором. Большинство оберток над средой (рис. 3) были разработаны для настройки функции вознаграждения, но некоторые из них также были призваны облегчить процесс обучения. Так, одним из таких значимых изменений была фильтрация обучаемых данных с акцентом на положения агента на или вблизи перекрестков. Также была применена техника “action masking”, помогающая избавляться от недопустимых действий при обучении [8].

Рассмотрим последние 4 обертки, разработанные для регулировки функции вознаграждения. Она претерпела значительные изменения. Были разработаны дополнительные компоненты, которые позволяли справиться с последствиями ее разреженной структуры, стимулировали агента, достигшего цели, и наказывали в обратной ситуации.

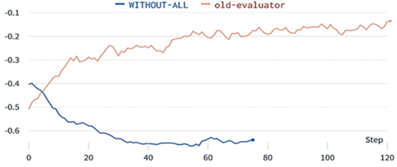
В предыдущих версиях соревнования функция вознаграждения не была разреженной, т.е. на каждом шаге агент получал пенальти за то, что он еще не доехал цели, кроме этого, на концах также давалось награда за общее положение дел. В этот раз организаторы усложнили задание главным образом для того, чтобы ввести концепцию расписания в общую постановку задачи. Поэтому модель не обучалась в исходном виде (WITHOUT-ALL). Тогда как для предыдущей структуры вознаграждения (old-evaluator) та же самая модель давала неплохие результаты (рис. 4).

Поэтому структура функции вознаграждения была сильно модифицирована. В общем виде формулу вознаграждения можно представить в виде

где r – исходная функция вознаграждения, F – формирующая функция вознаграждения, r' – модифицированная функция вознаграждения.

В базовых решениях к конкурсу предлагался терминальный вариант формирующей функции F_DR, нацеленный на обнаружение и борьбу с пробками. Предлагаемая компонента добавляла в функцию награды “штраф” за поведение, вызвавшее блокировку пути (рис. 3 Deadlock wrapper). Эта обертка идентифицирует агента в пробке, дает ему за это штраф и заканчивает для него эпизод. Но в сочетании с новой структурой вознаграждений она приводила к тому, что агенты вместо того, чтобы сторониться пробок, наоборот, стремились попасть в них. Это поведение агентов можно объяснить тем, что при больших наказаниях за опоздания легче всего было закончить эпизод пораньше и получить прибыль из-за того, что эпизод закончился раньше времени прибытия.

Поэтому данная идея была преобразована в более общий вид, а именно использовалась F_AR (рис. 3 Adjust wrapper), которая может быть представлена следующим образом:

где F_AR – терминальный корректирующий компонент функции формирования вознаграждения F, ${{r}_{{fin}}}$ – настраиваемое вознаграждение за завершение эпизода в нужном пункте назначения, ${{r}_{{notfin}}}$ – настраиваемый штраф за завершение эпизода не на станции назначения агента.

Данная компонента в любом случае дожидалась конца эпизода и давала пенальти за пробку или неприбытие и дополнительное поощрение за достижение цели. Также она нормализовала пошаговое вознаграждение, на котором стоит остановиться более подробно.

Чтобы уменьшить последствия разреженной функции вознаграждения, заданной в симуляторе, дополнительно была введена пошаговая награда, отражающая степень отставания поезда от графика движения (рис. 3 Time wrapper). В общем виде она может быть представлена следующими формулами:

где F_TR – временная составляющая функции формирования вознаграждения, ${{d}_{{max}}}$ – это заданная максимально возможная задержка агента по его расписанию; P_max – настраиваемый максимальный штраф; ${{t}_{r}}$ – оставшееся время до прибытия по расписанию.

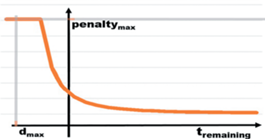
С одной стороны, этот компонент функции формирования вознаграждения соответствует новым требованиям учета расписания поезда. С другой – это напоминает пошаговое наказание из старой структуры вознаграждения Flatland за каждый временной шаг, сделанный в среде, пока есть достаточно времени до последнего прибытия агента. Когда время до последнего заезда истекает, штраф сильно возрастает. Смысл ее отражает график на рис. 5.

Такая модификация структуры функции вознаграждения радикально преобразовала характер обучения модели в лучшую сторону. Она стимулировала агента находиться в пути не слишком долго и в то же время следовать заданному графику движения.

Для лучшего ориентира к цели была разработана компонента F_DR (рис. 3 Distance wrapper), которая добавляла награду за приближение агента к пункту назначения и наказывала в случае простоя:

где F_DR – путевая компонента формирующей функции вознаграждения, σ – коэффициент для нормализации путевой компоненты вознаграждения, Δd – дельта расстояния, пройденного агентом на текущем шаге, ${{N}_{i}}$ – количество последних шагов простоя агента (в случае простоя), ${{P}_{i}}$ – штраф за простой. Штраф за простой увеличивался с увеличением времени простоя. Этот вроде бы полезный Wrapper имеет один неприятный нюанс. Его нужно дозировать в минимальном количестве, чтобы у агентов не появилось нездоровое желание совсем не заканчивать эпизод, а как можно дольше “двигаться к цели”.

Таким образом, суммарная функция награды была сформирована следующим образом:

где a, b, c – коэффициенты для настройки совместного поведения, R – общая функция вознаграждения, r – исходная функция вознаграждения.

Стратегия обучения

Для постепенного обучения на более сложных уровнях симуляции была разработана стратегия обучения по расписанию (curriculum learning). Был сконструирован ряд сред с различным уровнем сложности. Каждый уровень добавлял в среду новую особенность задачи, будь то увеличение количества поломок, скоростные режимы или более сложное соотношение городов и агентов. Обучение начиналось с очень маленькой среды из 2 агентов и 2 городов, затем постепенно усложнялось в соответствии с правилом: если текущая среда не доросла до следующего уровня сложности, увеличивалось только соотношение агентов и городов, в противном случае производился переход на следующую по сложности среду.

Событие перехода на новую среду было основано на достижении следующих условий в отношении обучаемого процесса:

– с момента последнего переключения среды было произведено достаточное количество шагов обучения;

– производная линии регрессии вознаграждений не превышает заданного значения;

– текущая оценка решения и процент выполнения превышают указанные пороговые значения.

Данная стратегия вместе с предложенными условиями перехода позволили процессу обучения вовремя справляться с каждым уровнем сложности и постепенно приспосабливаться к новым особенностям среды.

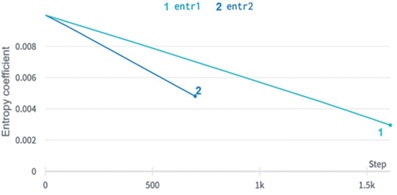
Также для регуляризации и предотвращения преждевременной сходимости был установлен график плавного спада энтропии. График энтропии оказался очень значимым фактором в обучении по расписанию. Настроив ее плавный спад, мы смогли обучить модель на более сложных уровнях среды.

6. РЕЗУЛЬТАТЫ

Для оценки результатов работы предложенных методов был проведен анализ графиков обучения по ряду характеристик, включая средний счет в эпизоде (episode score mean) и процент успешных агентов (percentage done).

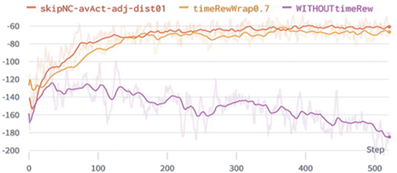
На рис. 6 проиллюстрирован эффект применения техники структурирования вознаграждений, а именно обучение без и с дополнительной временной компонентой (WITHOUTtimeRew и timeRewWrap0.7). Как видно из графика, добавление к структуре функции награды разработанной добавочной функции F_TR дает существенный вклад в успешность всего процесса обучения. В дополнение к этому, применение “action masking” и формирующих функций F_DR и F_AR дало небольшое улучшение в счете и скорости сходимости (skipNC-avAct-adj-dist01).

На рис. 7 представлен episode score mean для обучения модели по разработанному расписанию.

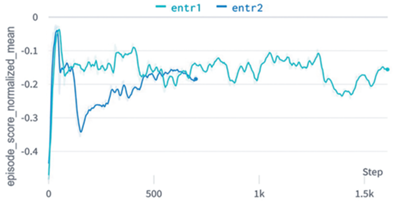
На рис. 8 показано обучение по двум различным режимам, на темно-синем энтропия спадает более резко, а на голубом – медленно. Можно заметить, что темно синий, хоть и быстро достиг вначале приемлемого значения показателей, но при дальнейшем обучении на новой среде не смог перейти на новый уровень сложности, т.к. начал преждевременно сходиться к локальному максимуму.

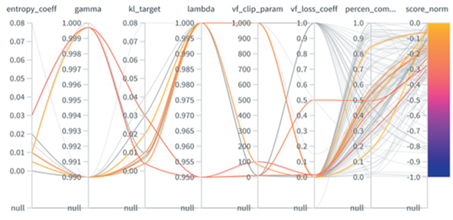
Настройка параметров данной модели проиллюстрирована на рис. 9. Больше информации об этом можно найти в [13].

Расширенный механизм наблюдений агента показал немного лучшие результаты, чем базовое наблюдение “Tree observation”, иллюстрируя особую чувствительность агентов к компонентам наблюдений.

7. ВЫВОДЫ

В данной работе предлагается стратегия решения задачи мультиагентного планирования железнодорожных перевозок. Описанное решение, основанное на обучении с подкреплением, заняло первое место в треке RL соревнования Flatland 3. В статье раскрывается задача, поставленная перед участниками соревнования, описываются ее основные сложности и предлагаются методы по их решению. Для решения поставленной задачи был разработан новый подход к проблеме планирования поездов на основе специальной техники структурирования вознаграждения, которая стимулировала агента следовать заданному графику движения. Данная методика вместе с дальнейшей настройкой параметров внесли наибольший вклад в производительность модели.

Кроме того, была разработана стратегия обучения по расписанию, которая позволила процессу обучения вовремя справляться с каждым уровнем сложности и дала возможность обучить модель в более сложных условиях с повышенным уровнем поломок. Полученные результаты показали эффективность разработанных методов. Тем не менее остается большая область для дальнейшего совершенствования и проведения научных исследований в области повышения быстродействия и эффективности алгоритма.