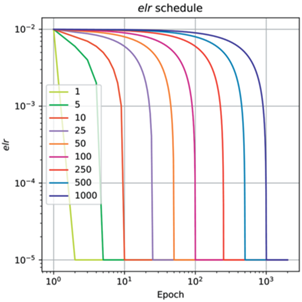
Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 508, № 1, стр. 50-69
ДИНАМИКА И ЛАНДШАФТ ФУНКЦИИ ПОТЕРЬ ДЛЯ ГЛУБОКИХ НЕЙРОННЫХ СЕТЕЙ ПРИ ОБУЧЕНИИ С КВАДРАТИЧНОЙ ФУНКЦИЕЙ ПОТЕРЬ
М. С. Находнов 1, М. С. Кодрян 2, Е. М. Лобачева 2, Д. С. Ветров 1, 2, *
1 Институт искусственного интеллекта AIRI
Москва, Россия
2 Национальный исследовательский университет “Высшая школа экономики”
Москва, Россия
* E-mail: dvetrov@hse.ru
Поступила в редакцию 28.10.2022
После доработки 28.10.2022
Принята к публикации 01.11.2022
- EDN: TUHJHE
- DOI: 10.31857/S2686954322070189
Аннотация
Знание свойств геометрии функции потерь позволяет успешно объяснять поведение нейронных сетей, динамику их обучения, взаимосвязь получаемых решений и гиперпараметров, таких как способ регуляризации, архитектура нейронной сети или расписание темпа обучения. В данной работе изучаются динамика обучения и поверхность стандартной кросс-энтропийной и популярной в последнее время квадратичной функций потерь для масштабно инвариантных сетей с нормализацией. Для устранения симметрий был произведен переход к оптимизации на сфере, который позволил обнаружить три фазы обучения в зависимости от размера шага обучения на сфере, обладающие принципиально разными свойствами, – фазу сходимости, фазу хаотического равновесия и фазу дестабилизированного обучения. Данные фазы наблюдаются для обеих исследованных функций потерь, однако при обучении с квадратичной функцией потерь нужны бо́льшие сети и более долгое обучение для перехода в фазу сходимости.
1. ВВЕДЕНИЕ
Одной из основных задач, успешно решаемых с помощью глубоких нейронных сетей, является многоклассовая классификация. Важной составляющей решения задачи является правильный выбор функции потерь. В большинстве случаев, в задаче классификации ограничиваются использованием кросс-энтропийной функции потерь. При этом данный выбор не является единственно возможным и есть свидетельства, что альтернативные варианты функции потерь могут приводить к качеству не хуже на большом классе задач и архитектур [1].
С другой стороны, решения современных задач в машинном обучении широко используют эмпирические приемы для получения наилучших результатов. Например, выбор оптимизатора или расписания темпа обучения долгое время основывался на эмпирических результатах для конкретных архитектур [2]. Исследование ландшафта функции потерь позволило как обосновать такие инженерные техники, как батч-нормализация [3], соединения быстрого доступа (Residual Connections) [4], так и предложить новые способы улучшения генерализации моделей [5].
Известно, что ширина оптимума имеет сильную корреляцию генерализацией модели [6]. Поэтому при анализе ландшафта функции потерь ширина в текущей точке и динамика ее изменения в процессе обучения вызывают основной интерес.
Исследование поверхности функции потерь затруднено, так как оптимизация происходит в многомерном пространстве, а функция, задаваемая глубокой нейронной сетью, является невыпуклой. Наличие в сетях слоев нормализации еще сильнее усложняет анализ за счет появления масштабно инвариантных симметрий. Переход к оптимизации на сфере позволил избавиться от таких симметрий. При варьировании разрешающей способности на сфере было обнаружено три режима обучения нейронной сети, отвечающих различным областям поверхности функции потерь. В данной работе был проведен анализ этих фаз с точки зрения генерализации моделей и ширины получаемых решений. Также было произведено сравнение различных функций потерь с точки зрения влияния на обнаруженные фазы и динамику обучения.
2. ДИЗАЙН ЭКСПЕРИМЕНТОВ
2.1. Симметрии в нейронных сетях
Исследование нейронных сетей осложняется значительным уровнем избыточности параметров [7] и наличием внутренних симметрий. Простейшими примерами таких симметрий являются согласованная перестановка нейронов в последовательных слоях и согласованное масштабирование весов в сетях с функцией активации ReLU [8]. Такие преобразования обычно оставляют сеть функционально неизменной, хотя в пространстве весов модель может существенно измениться. Другой важной симметрией является масштабная инвариантность в сетях с батч-нормализацией. Использование батч-нормализации после сверточного слоя приводит к тому, что умножение весов, предшествующих слою нормализации, не меняет сеть, как функцию от своего входа. Рассмотрим нейронную сеть $f\left( {{\theta }} \right)$ с весами ${{\theta }} \in {{R}^{d}}$. Параметры, умножение которых на произвольный положительный коэффициент α не меняет функциональный вид сети, будем называть масштабно инвариантными (Scale-Invariant, SI). В таком случае, для SI параметров верно:
(1)
$\begin{array}{*{20}{c}} {f\left( {\alpha \theta } \right) = f\left( \theta \right),\,\,\forall \,\,\theta ,\alpha > 0} \end{array},$(2)
$\begin{array}{*{20}{c}} {\nabla f\left( {\alpha \theta } \right) = \frac{1}{\alpha }\nabla f\left( \theta \right)} \end{array}.$Наличие SI параметров в сети приводит к неоднозначности в определении ширины оптимума, так как в зависимости от нормировки весов функционально одинаковые модели будут иметь различные градиенты и вторые производные в соответствии с уравнением (2). Для того, чтобы избавиться от инвариантности, предлагается рассматривать сети, состоящие только из масштабно инвариантных параметров на сфере фиксированного радиуса. Для определенности будем по умолчанию считать, что сеть задана на единичной сфере, т.е. $\theta \in B{\text{\_}}\left\{ 1 \right\} = \{ \theta {\text{|}}~\,\left| {\left| \theta \right|} \right| = 1\} $. Темп обучения сети с полностью масштабно инвариантными параметрами (Fully Scale-Invariant, FSI) на сфере единичного радиуса будем называть эффективным темпом обучения (effective learning rate, elt). Обучение такой модели градиентными методами может приводить к тому, что после очередного шага норма весов станет отличной от $1$. В таком случае предлагается применять нормировку весов на очередном шаге. Отличие данного подхода от Римановой оптимизации на сфере приведено в Приложении 3 .
Стоит отметить, что фиксация общей нормы параметров устраняет только часть симметрии в нейронной сети – отдельные фильтры сверхточных слоев остаются инвариантными к перенормировке.
Для исследования эффектов, связанных с динамикой оптимизации, вдоль поверхности функции потерь необходимо выбрать такую постановку эксперимента, где особенности обучения будут изолированы от сторонних эффектов, таких как переобучение, симметрии внутри нейронной сети. Для этого предлагается рассматривать следующие контролируемые, но в тоже время приближенные к реальным, условия для обучения. Во-первых, в качестве обучающей выборки будет рассматриваться набор данных CIFAR10 без использования аугментации. Во-вторых, в качестве архитектуры нейронной сети используется сверточная нейронная сеть ConvNet с батч-нормализацией из полностью масштабно инвариантных параметров. Переход к FSI архитектуре производится путем фиксации аффинных слоев батч-нормализации и фиксации последнего линейного слоя сети. Подробное описание архитектуры находится в Приложении 1 . Известно, что такие ограничения на параметры не влияют на итоговое качество модели на тестовой выборке. В-третьих, обучение происходит с помощью стохастического градиентного спуска (Stochastic gradient descent, SGD) без использования инерции и $L_{2}$ регуляризации. Все модели обучаются из одного и того же начального приближения с одинаковым порядком батчей в процессе оптимизации.
В качестве функции потерь рассматриваются две альтернативы. Стандартным выбором для оптимизируемой ошибки для задачи $C$-классовой классификации является кросс-энтропия:
(3)
$\begin{array}{*{20}{c}} {L\left( {\hat {y},y} \right) = - \log \frac{{\exp \widehat {{{y}_{y}}}}}{{\mathop \sum \nolimits_{i = 1}^C \exp \widehat {{{y}_{i}}}}}} \end{array},$В качестве альтернативы можно рассмотреть квадратичную функцию потерь:
(4)
$\begin{array}{*{20}{c}} {L\left( {\hat {y},y} \right) = \mathop \sum \limits_{i = 1}^C {{{(\widehat {{{y}_{i}}} - 1\left[ {y = i} \right])}}^{2}}} \end{array}.$Существующие работы не дают четкого ответа о том, какая из этих функций предпочтительнее. С одной стороны, долгое время считалось, что квадратичная функция потерь медленнее сходится и приводит к худшему качеству на тестовой выборке при использовании стохастического градиентного спуска [9, 10].
Однако более новые работы показывают противоположную ситуацию – подробный анализ [1] на широком классе архитектур и задач показал паритет по качеству при незначительно более медленной скорости сходимости квадратичной функции потерь.
С теоретической точки зрения также нет окончательного ответа. При большой степени перепараметризации, которая свойственна нейронным сетям, и достаточно строгих условиях было показано, что функционально решения с использованием кросс-энтропийной функции потерь и квадратичной функции потерь в точности совпадают [11]. Однако существующие работы не дают ответа на то, можно ли расширить результаты на современные архитектуры глубоких нейронных сетей.
В качестве основных объектов исследования были выбраны среднее значение функции потерь на обучающей выборке ${{L}_{T}}$, доля неверно классифицированных объектов на обучающей и тестовой выборках ${{E}_{T}},{{E}_{t}}$ и метрика кривизны $GM = {{E}_{b}}\left| {\left| {\nabla {{L}_{b}}\left( {{\theta }} \right)} \right|} \right|$.
2.2. Метрики кривизны
В качестве основной метрики ширины предлагается использовать среднюю норму градиентов по отдельным батчам обучающей выборки $GM$. Интуитивно данная метрика показывает, насколько велик разброс градиентов по отдельным объектам в точке пространства весов. В плоских, широких областях данная метрика должна быть мала, в узких – велика.
На практике такая метрика хорошо коррелирует с метриками кривизны второго порядка, такими как след матрицы Фишера или максимальное собственное значение матрицы Гессе. Теоретический анализ также подтверждает высокую корреляцию между данными метриками [12]. При этом вычисление $GM$ требует только одного обратного прохода, в отличие от двух обратных проходов при вычислении оценок на статистики Гессиана и матрицы Фишера. Более того, за счет усреднения по батчам, а не по отдельным объектам получается существенно ускорить вычисление оценки кривизны, не теряя в качестве приближения. Сравнение данных метрик приведено в Приложении 2 .
3. ОБУЧЕНИЕ С КРОСС-ЭНТРОПИЙНОЙ ФУНКЦИЕЙ ПОТЕРЬ
Для анализа динамики обучения нейронных сетей были обучены FSI модели с различными значениями elr для кросс-энтропийной функции потерь.
На рис. 1 видно, что модели разделились на три условных группы. В первой группе модели сходятся в область с широкими минимумами и низким значением функции потерь. Во второй – модели лосс и кривизна колеблются около некоторого значения, как видно на верхних графиках рис. 2. В последней группе модели с наибольшей кривизной.
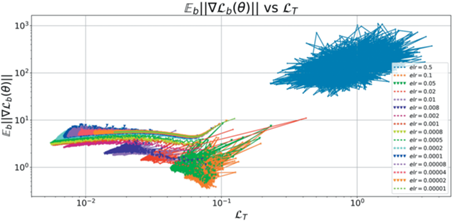
Рис. 1.
Фазовая диаграмма для кривизны и кросс-энтропийной функции потерь для различных elr для сети ConvNet. Наблюдается три принципиальных режима поведения траекторий.
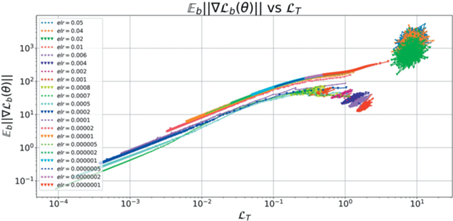
Рис. 2.
Основные метрики для различных elr. Крайняя правая диаграмма демонстрирует скачкообразные переходы между фазами при изменении elr.
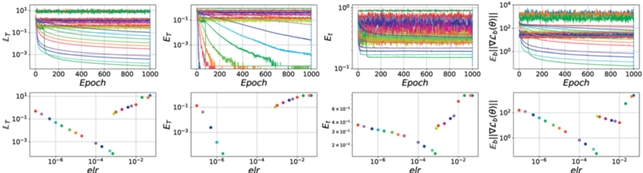
Проанализируем каждую группу по отдельности.
3.1. Первая фаза
К первой фазе отнесем модели, для которых $elr \leqslant 7 \times {{10}^{{ - 4}}}$. Данные модели выделяются тем, что с увеличением elr происходит согласованное уменьшение всех метрик в конце обучения. Верхняя граница фазы определяется резким изменением всех метрик (нижние графики рис. 2), что свидетельствует о качественном изменении поведения при переходе через указанную границу. При этом первую фазу можно условно разбить на две подфазы – модели, которые достигают нулевой ошибки на обучающей выборке к концу обучения (сошедшаяся первая фаза) и все остальные модели с меньшими elr (не сошедшаяся первая фаза).
Для анализа первой фазы исследуем линейную связность моделей (mode connectivity). Для этого рассмотрим две модели $f\left( {{\theta }} \right)$, параметризованные весами θ1, θ2. Под mode connectivity будем подразумевать значения метрик для моделей на отрезке между парой исходных точек $f({{\alpha }}{{{{\theta }}}_{1}}\, + \,(1\, - \,{{\alpha }}){{{{\theta }}}_{2}})$, α ∈ [0, 1]. Будем называть модели линейно связными или лежащими в одной области, если на графике mode connectivity отсутствуют ярко выраженные экстремумы в промежуточных точках ${{\alpha }} \in \left( {0,1} \right)$. Иначе, будем называть модели линейно несвязными.
Модели, которые не достигают нулевой ошибки ввиду маленького темпа обучения, сходятся в одну линейно связную область. При больших темпах обучения модели успевают разойтись в разные оптимумы, что приводит к наличию пика у значения функции потерь на Графике mode connectivity 3. Стоит отметит, что точная граница между подфазами проходит не по нулевой ошибке на обучении, но по ошибке порядка 10–15 объектов.
Таким образом, при $elr \leqslant 8 \times {{10}^{{ - 7}}}$ модели сходятся в одну и ту же область, но с разной скоростью, что также подтверждается совпадением их траекторий на фазовой диаграмме 1.
По достижении достаточно низкой ошибки на обучении модели начинают сходиться вдоль различных траекторий. При этом увеличение темпа обучения приводит к монотонному росту генерализации. Это хорошо согласуется с тем, что при больших elr разрешающая способность сети уменьшается, что приводит к сходимости во все более и более широкие, плоские области, которые в свою очередь и определяют лучшее качество на тестовой выборке. Дальнейший рост elr приводит к тому, что сеть резко перестает сходиться к нулевой ошибке на обучении и качественно меняет свое поведение. Таким образом, данный эксперимент подтверждает утверждение, что лучшая генерализация достигается в самом широком оптимуме, при условии сходимости сети.
Также отсутствие линейной связности в первой фазе при достаточно больших elr показывает, что модели сходятся в разные области пространства весов. Покажем, что внутри каждой из этих областей нет минимумов меньшей ширины. Для этого дообучим модели в течение $5000$ итераций, резко уменьшив темп обучения в $2$ и в $10$ раз.
На диаграмме 4 видно, что уменьшение elr не меняет динамику обучения моделей. Это косвенно подтверждает, что глобальные свойства оптимума остаются стабильными и внутри оптимума заданной ширины нет минимума с меньшей шириной.
Mode connectivity на рис. 5 также подтверждает, что уменьшение elr не приводит к сходимости в линейно несвязные оптимумы.
Рис. 3.
Mode connectivity для разных моделей из первой фазы. Слева – модели из не сошедшейся первой фазы. Справа – сошедшаяся первая фаза. После достижения сходимости области оптимумов для разных elr оказываются линейно несвязными.
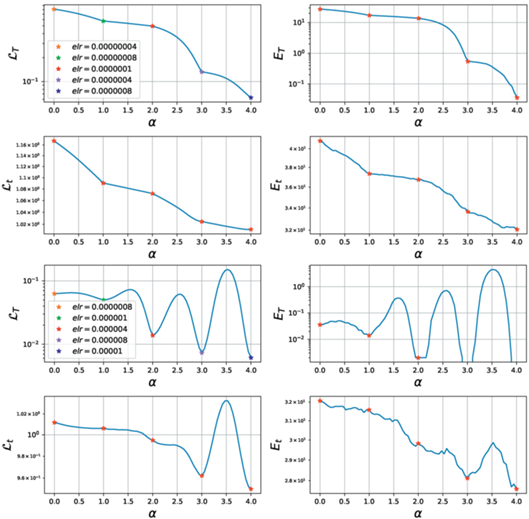
Рис. 4.
Фазовая диаграмма при уменьшении elr для ConvNet. Итоговый elr обозначен как $\widehat {elr}$. Траектории продолжают исходный тренд, что говорит о “застревании” в фиксированной области в окрестности локального минимума.
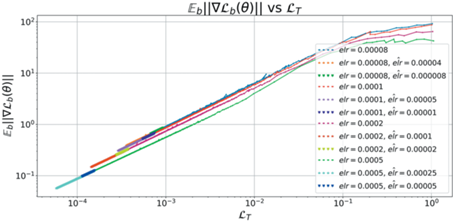
Рис. 5.
Mode connectivity для моделей с уменьшенным elr. Так как модели достигли нулевой ошибки на обучении, то соответствующие точки на графиках для ET не отображаются. Модели остаются линейносвязными.
Теперь рассмотрим поведение сетей при увеличении elr. В зависимости от величины итогового elr возможны несколько принципиальных ситуаций. При небольших коэффициентах увеличения динамика сети меняется слабо. Как видно из рис. 6, 7, модель остается в том же оптимуме с точки зрения генерализации и метрики кривизны.
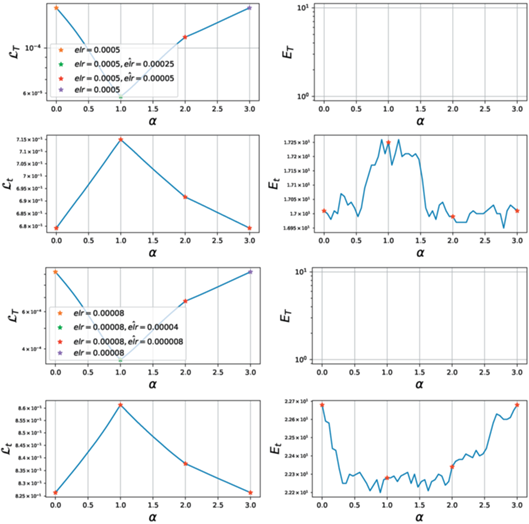
Рис. 6.
Mode connectivity для elr = 0.0001 при дообучении с большим темпом. При малых увеличениях (левая панель) точки остаются линейно связными. Более сильное увеличение $\widehat {elr}$ приводит к переходу в окрестность другого оптимума (правая панель). Модели, достигшие нулевой ошибки на обучении, на отображаются на графиках для ET.
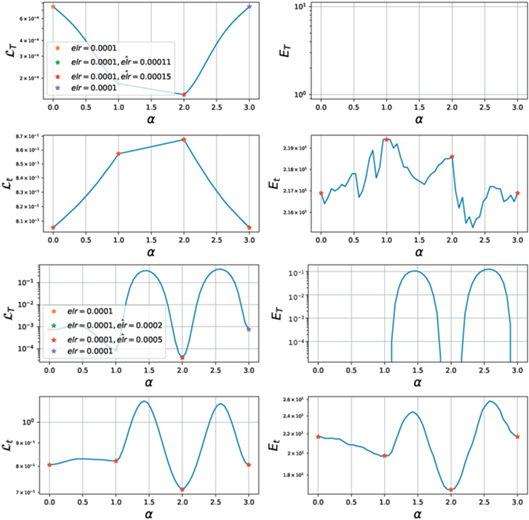
Рис. 7.
Фазовые диаграммы для elr = 0.0001 при дообучении с бо́льшим темпом. Малые увеличения elr не выводят модель из исходного оптимума.
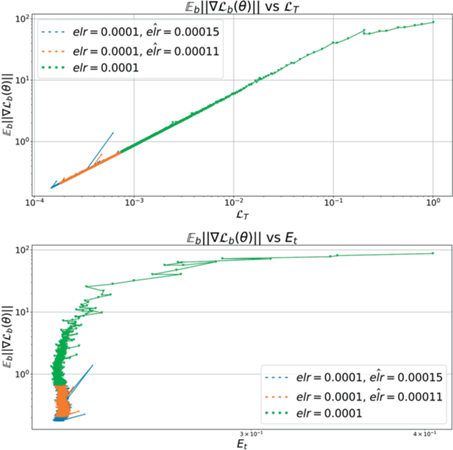
При дальнейшем увеличении итогового elr сеть начинает обучаться менее стабильно и в какой-то момент наблюдается “скачок” и переход на новую траекторию. Значения ${{E}_{t}}$ показывают, что модель может сойтись в незначительно отличающиеся по качеству минимумы. Результаты демонстрируют, что при наличии скачков во время дообучения предыстория обучения влияет слабо, т.е. модель после выхода из региона нестабильности возвращается на траекторию, которая соответствует изначальному обучению с итоговым $\widehat {elr}$.
Наконец, если итоговый elr превосходит верхнюю границу первой фазы, то модель быстро расходится и переходит в область, которая соответствует обучению с нуля с темпом обучения во второй фазе.
3.2. Вторая фаза
При увеличении темпа обучения до $8 \times {{10}^{{ - 4}}}$ происходит переход в следующую зону: все метрики быстро, в течение первых 5–10 итераций, выходят на фиксированный средний уровень и не меняются в процессе обучения. Переход в новую фазу сопровождается резким скачком всех метрик. При этом во второй фазе модель сходится не к случайным предсказаниям, а к значительно лучшему качеству на обучающей выборке. С увеличением elr модель сходится все хуже и хуже до тех пор, пока она не перейдет в третью фазу. Интересно, что в данной фазе увеличение $elr$ приводит к уменьшению кривизны.
Можно предположить, что различие между первой и второй фазой вызвано наличием в пространстве весов области с высокой кривизной, которую необходимо преодолеть для достижения низкого значения функции потерь. На фазовой диаграмме можно видеть характерный загиб на траекториях моделей из первой фазы в области ${{L}_{T}} \sim {{10}^{{ - 1}}} - 2 \times {{10}^{0}}$, при прохождении которой наблюдается локальный пик кривизны.
Во второй фазе веса сети не сходятся и на соседних итерациях вектора весов менее коррелированы, чем в первой фазе и с ростом elr корреляция падает, что видно из рис. 10.
Рис. 8.
Фазовые диаграммы для elr = 0.0001 при дообучении с большим темпом. На обеих диаграммах виден ступенчатый переход с одной траектории на другую при переходе в другой, более плоский оптимум.
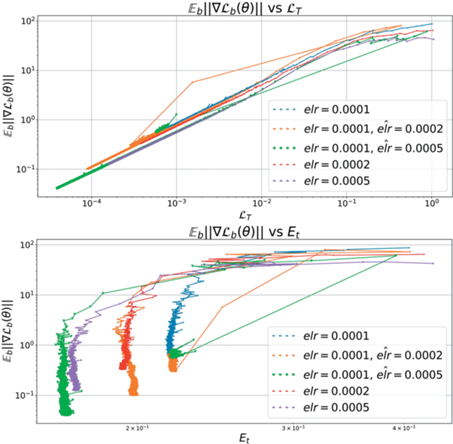
Рис. 9.
Фазовые диаграммы для elr = 0.0001 при дообучении с большим темпом. При этом происходит мгновенный переход в хаотический режим.
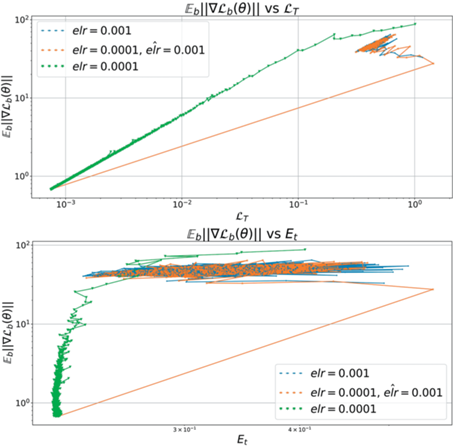
Рис. 10.
Распределение косинусных расстояний между всеми соседними эпохами для различных темпов обучения показывает разделение фаз обучения между собой.
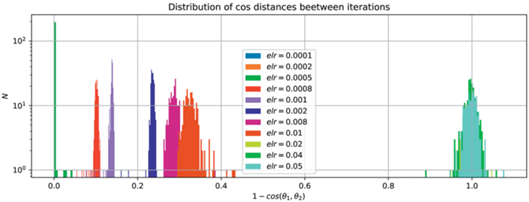
Дальнейшее увеличение elr приводит к тому, что веса на соседних итерациях не коррелируют друг с другом, что соответствует переходу в третью фазу.
Исследуем свойства моделей во второй фазе. В течение всей 1000 итераций не наблюдается значительных изменений средних значений метрик. Модели из-за большого темпа обучения “застревают” на фиксированном уровне и могут уменьшить значения метрик только при условии перехода через “бутылочное горлышко” кривизны. Однако, так как в данной зоне градиенты слишком велики, такой переход возможен только при уменьшении шага SGD. Поэтому рассмотрим эксперимент с дообучением модели из второй фазы с резко уменьшенным elr.
Из рис. 11 видно, что при запуске из небольшого elr второй фазы модели ведут себя на фазовой диаграмме подобно тому, как происходил переход из первой фазы в первую на графике 4 – траектория продолжает тренд точек из второй фазы, сходясь в окрестность линии, соответствующей наибольшему темпу обучения первой фазы ($elr = 7 \times {{10}^{{ - 4}}}$), вне зависимости от итогового elr. При этом генерализация таких моделей превосходит лучшую генерализацию среди всех сетей, полученных в первой фазе. Некоррелированность $GM$ и ${{E}_{t}}$ в данном примере еще раз подчеркивает недостаток локальных метрик кривизны при использовании их как прокси для генерализации.
Рис. 11.
Фазовые диаграммы для $elr = {{10}^{{ - 3}}}$ при дообучении из второй фазы с меньшим темпом. Модели сходятся к самому широкому оптимуму.

Запуск дообучения из большего $elr = {{10}^{{ - 2}}}$ приводит к противоположным результатам. Во-первых, в соответствии с правым рис. 12 траектории таких моделей сходятся к тем же кривым, которые соответствуют моделям, обучавшимся с заданным elr изначально. Левый график показывает, что улучшение итогового качества наблюдается только при маленьких итоговых темпах обучения ($elr \leqslant {{10}^{{ - 4}}}$).
Рис. 12.
Фазовые диаграммы для $elr = {{10}^{{ - 2}}}$ при дообучении из второй фазы с меньшим темпом. Модели сходятся к оптимумам различной ширины.
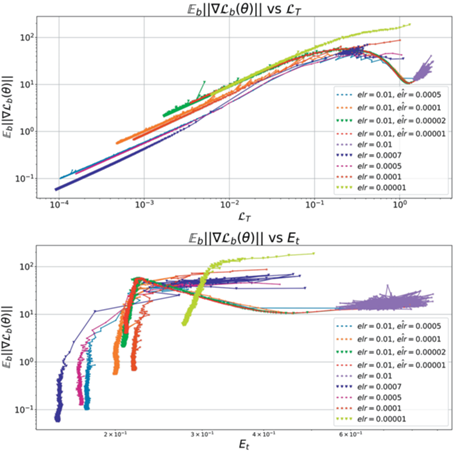
Сравнение результатов для большого и маленького elr второй фазы показывает, что пред-обучение во второй фазе тем больше влияет на итоговое тестовое качество ${{E}_{t}}$, чем меньше стартовый elr.
Также независимость итогового качества и траектории при дообучении из маленького elr второй фазы позволяет выдвинуть гипотезу, что выбор оптимума в первой фазе осуществляется в момент перехода из второй фазы в первую в самом начале обучения. Для проверки этого утверждения поставим следующий эксперимент: зафиксируем стартовый $elr = {{10}^{{ - 2}}}$ и запустим дообучение с кусочно-линейным расписанием темпа обучения 13.
Из рис. 14 видно, что, изменяя скорость уменьшения elr, можно получить спектр траекторий, где на одном конце сходимость вдоль линии, соответствующей наибольшему elr$elr$ первой фазы, а на другом, при самом быстром изменении elr – траектория модели для $\widehat {elr}$ без предобучения. Медленное уменьшение elr из второй фазы приводит к тому, что модель будет постепенно переходить на траектории, соответствующие меньшим elr второй фазы, до тех пор, пока модель не выскочит в область с меньшей кривизной.
Рис. 14.
Фазовые диаграммы для $elr = {{10}^{{ - 2}}}$ при дообучении в $\widehat {elr} = {{10}^{{ - 5}}}$ с различными расписаниями. Δ – длительность перехода.
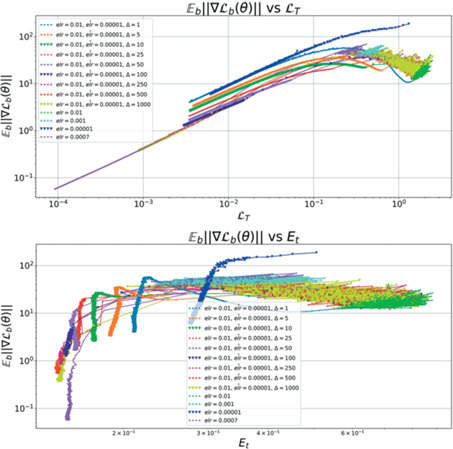
Величина прироста качества на тестовой выборке ${{E}_{t}}$ также плавно зависит от скорости уменьшения elr. Таким образом, можно предположить, что оптимальной стратегией для расписания elr является как можно дольше находиться в точках второй фазы, прежде чем перейти в первую, так как в момент перехода модель “фиксирует” минимум, в который она будет сходиться. Изменить минимум в первой фазе можно, только существенно увеличив elr и добившись нестабильности в обучении, которая позволит “перескочить” в область с другими функциональными характеристиками.
3.3. Третья фаза
Рассмотрим оставшиеся модели, соответствующие $elr \geqslant ~2 \times {{10}^{{ - 2}}}$. При дальнейшем увеличении elr во второй фазе снова происходит качественное изменение поведения – градиенты у модели резко увеличиваются, ошибка на обучении становится равной случайному гаданию (90% в случае 10 классов). Переход в эту зону соответствует переходу к случайному предсказанию. Для проверки этого утверждения было выполнено обучение модели, в которой каждый шаг градиентного спуска заменялся на шаг вдоль случайного направления той же магнитуды. Также, для сравнения, был поставлен эксперимент, где в качестве очередного шага вместо антиградиента используется градиент. Полученные результаты показывают, что случайное блуждание и движение по градиенту позволяют ограничить наблюдаемое поведение кривизны в третьей фазе снизу и сверху.
4. ОБУЧЕНИЕ С КВАДРАТИЧНОЙ ФУНКЦИЕЙ ПОТЕРЬ
Теперь сравним поведение на фазовых диаграммах для квадратичной функции потерь (Mean Squared Error, MSE). Известно, что решение задачи регрессии сложнее, чем решение задачи классификации [11], следовательно, обучение с квадратичной функцией потерь требует большего числа итераций до сходимости. Поэтому в экспериментах с MSE все модели будем обучать 6000 итераций.
Анализ фазовой диаграммы 16 позволяет четко отделить третью фазу ($elr=0.5$) и не сошедшуюся часть первой фазы ($elr~ \lesssim 0.0001$). Остальные модели визуально напоминают как первую, так и вторую фазу для кросс-энтропии. Для более точного анализа рассмотрим распределение косинусных расстояний для последовательных моделей вдоль траектории обучения. Из рис. 17 видно, что модели c $elr~ \gtrsim 0.02$ можно отнести ко второй фазе. Остальные – отнесем к первой фазе.
Рис. 15.
Основные метрики в третьей фазе. Синяя линия – случайное блуждание, оранжевая линия – движение по градиенту. Обучение в третьей фазе схоже со случайным блужданием.

Рис. 17.
Распределение косинусных расстояний между соседними эпохами для различных темпов обучения при обучении с квадратичной функцией потерь.
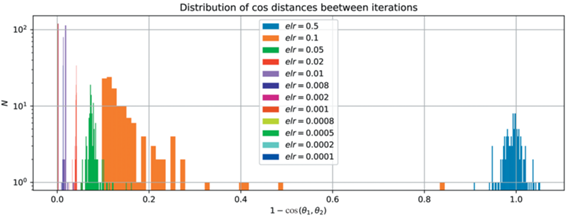
Теперь соотнесем такое разделение на фазы с поведением метрик на рис. 18. Видно, что ни одна из моделей не сошлась к нулевой ошибке на обучающей выборке, что еще раз подтверждает, что модели с квадратичным лоссом сходятся медленнее моделей с кроссэнтропийной функцией потерь. Другим отличием является тот факт, что граница между первой и второй фазами более размытая. Действительно, модели с $elr \sim 0.008{\kern 1pt} - {\kern 1pt} 0.02$ монотонно уменьшают число неправильно классифицированных объектов, при этом оставаясь в области с фиксированой шириной. Это контрастирует с первой фазой кросс-энтропии, где лосс и кривизна убывали согласовано вдоль всей траектории.
Рис. 18.
Основные метрики для различных elr для ConvNet с квадратичной функцией потерь. График ошибки на тесте указывает на наличие двух фаз обучения.
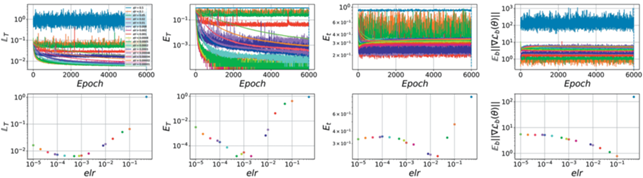
Так как на всей выборке из 50 000 объектов модели с MSE лоссом не достигают сходимости, обучим сети на подвыборке объемом 10%.
В таком случае метрики 20 и фазовая диаграмма 19 становятся похожими на случай кроссэнтропии. По фазовой диаграмме можно четко выделить все три фазы обучения, а также две подфазы в первой фазе. Оптимальный elr с точки зрения ошибки на тестовой выборке соответствует наибольшему темпу обучения в первой фазе. В той же точке достигается минимальная кривизна.
По аналогии с кроссэнтропийной функцией потерь рассмотрим эксперимент с дообучением с различными elr.
Анализ результатов показывает, что уменьшение elr из траекторий, относящихся к первой фазе, приводит к поведению, с одной стороны, согласованному с кроссэнтропией – траектории продолжают двигаться вдоль того же тренда, что был и до уменьшения темпа. При этом функция потерь убывает. Однако, в отличие от кроссэнтропии, где кривизна монотонно убывала, для квадратичного лосса $GM$ или стабилизируется ($elr \approx {{10}^{{ - 2}}}$, граница между первой и второй фазами), или даже начинает возрастать (меньшие elr). Такое поведение свидетельствует о начале переобучения, что более четко видно на правом графике 21 – сначала ${{E}_{t}}$ убывает, но затем начинает резко расти.
5. ВЫВОДЫ
Проведенные исследования показали наличие нескольких фаз обучения полностью масштаб инвариантных сетей на сфере в зависимости от темпа обучения.
При этом первая фаза обучения соответствует сходимости весов в оптимум фиксированной ширины.
Вторая фаза определяется хаотическим равновесием, при котором метрики для сети стабилизируются около некоторого уровня. При этом область, в которой стабилизируется нейронная сеть, во второй фазе оказывает решающее влияние на итоговое качество модели.
Третья фаза характеризуется переходом к блужданию по сфере, корреляция между различными моделями на соседних итерациях отсутствует.
Выявленные фазы проявляются для разных функций потерь, как для квадратичного лосса, так и для кросс-энтропии. Исследование в Приложении 4 показывает, что выводы воспроизводятся в том числе и на сетях с не масштабно инвариантными параметрами и с регуляризацией.
Также результаты дополнительно подтверждают гипотезу о том, что для MSE требуется большее число итерации или большее число параметров у сети для сходимости к схожему качеству по сравнению с кросс-энтропией.
Список литературы
Hui L., Belkin M. Evaluation of Neural Architectures Trained with Square Loss vs Cross-Entropy in Classification Tasks, 2021.
Smith L.N. Cyclical Learning Rates for Training Neural Networks, arXiv, 2015.
Santurkar S., Tsipras D., Ilyas A., Madry A. How Does Batch Normalization Help Optimization?, arXiv, 2018.
He F., Liu T., Tao D. Why ResNet Works? Residuals Generalize, arXiv, 2019.
Foret P., Kleiner A., Mobahi H., Neyshabur B. Sharpness-Aware Minimization for Efficiently Improving Generalization, arXiv, 2020.
Jiang Y., Neyshabur B., Mobahi H., Krishnan D., Bengio S. Fantastic Generalization Measures and Where to Find Them, arXiv, 2019.
Allen-Zhu Z., Li Y., Liang Y. Learning and Generalization in Overparameterized Neural Networks, Going Beyond Two Layers, arXiv, 2018.
Badrinarayanan V., Mishra B., Cipolla R. Understanding symmetries in deep networks, arXiv, 2015.
Bosman A.S., Engelbrecht A., Helbig M. Visualising Basins of Attraction for the Cross-Entropy and the Squared Error Neural Network Loss Functions, 2019.
Demirkaya A., Chen J., Oymak S. Exploring the Role of Loss Functions in Multiclass Classification, 2020 54th Annual Conference on Information Sciences and Systems (CISS), 2020.
Muthukumar V., Narang A., Subramanian V., Belkin M., Hsu D., Sahai A. Classification vs regression in overparameterized regimes: Does the loss function matter?, 2021.
Thomas V., Pedregosa F., van Merriënboer B., Manza-gol P.-A., Bengio Y., Roux N.L. On the interplay between noise and curvature and its effect on optimization and generalization,” ConferenceProceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics, 2020.
Lobacheva E., Kodryan M., Chirkova N., Malinin A., Vetrov D. On the Periodic Behavior of Neural Network Training with Batch Normalization and Weight Decay, 2021.
Simonyan K., Zisserman A. Very Deep Convolutional Networks for Large-Scale Image Recognition, arXiv, 2014.
Nakkiran P., Kaplun G., Bansal Y., Yang T., Barak B., Sutskever I. Deep Double Descent: Where Bigger Models and More Data Hurt, arXiv, 2019.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления