Доклады Российской академии наук. Науки о Земле, 2020, T. 493, № 1, стр. 58-62

ВВЕДЕНИЕ

Интерпретация геофизических аномалий представляет собой процедуры извлечения информации из данных наблюденных физических полей, в которых в скрытом виде содержится большой объем геологической информации. Основываясь на данных геофизики можно формально описать распределение физических свойств. При этом моделей, генерирующих наблюденное поле, может быть бесчисленное множество. Поэтому для выполнения содержательной интерпретации необходима вся имеющаяся априорная геолого-геофизическая информация по изучаемому объекту.

Одним из основных методов решения обратных задач геофизики является метод регуляризации. В 1960–1980-е гг. в трудах А.Н. Тихонова, В.К. Иванова, М.М. Лаврентьева, а также в работах их многочисленных учеников была создана классическая теория регуляризации систем линейных алгебраических уравнений (СЛАУ). Однако впоследствии В.Р. Страхов показал, что классическая теория регуляризации СЛАУ условиям и потребностям гравиметрии, магнитометрии, геодезии и геоинформатики не адекватна [1].

Предлагается новый подход, который позволяет описать множество решений, удовлетворяющих поставленной задаче, и затем найти среди этих эквивалентных решений то решение, которое наилучшим образом удовлетворяет имеющейся априорной информации о распределении свойств модели.

Конструктивное описание многообразия решений $\Phi (A,b)$ линейной системы $Ax = b$ в n-мерном евклидовом пространстве $E$ позволяет учесть априорную информацию о свойствах искомого решения ${{x}^{f}}$ путем его поиска на многообразии $\Phi (A,b)$.

Технически это выглядит следующим образом: точка зрения на искомое решение ${{x}^{f}}$ формализуется неотрицательным функционалом $F$ на $\Phi (A,b)$, и решение ${{x}^{f}}$ его минимизирует. Если точек зрения на ${{x}^{f}}$ несколько и за них отвечает система функционалов $\Phi = ({{F}_{1}}, \ldots ,{{F}_{k}})$, то поиск ${{x}^{f}}$ сводится к многокритериальному выбору $B(\Phi ,\Phi (A,b))$ относительно $\Phi $ на $\Phi (A,b)$.

Сказанное выше графически передает схема

• Первый переход полностью относится к линейной алгебре и состоит в эффективном построении ортогонального дополнения к любому подпространству в $E$.

• Второй переход формализует априорную информацию об искомом решении ${{x}^{f}}$ в систему функционалов $\Phi $ на многообразии $\Phi (A,b)$ и потому требует широкого спектра методов (нечеткая математика, машинное обучение и т.д.).

• Третий переход представляет собой в широком смысле оптимизацию $\Phi $ на $\Phi (A,b)$, включающую в себя как классические непрерывные методы (градиент, штрафные функции и т.д.), так и дискретные (теория выбора, нейронные сети и т.д.).

Конструктивное описание $\Phi (A,b)$ также получается в рамках теории ABS-алгоритмов [2], но, к сожалению, его компьютерная реализация неустойчива (несмотря на наличие управляющих параметров, шаг пересчета решения может быть очень большим). Поэтому в первой части работы мы предлагаем более простую и устойчивую на практике параметризацию $\Phi (A,b)$.

Предметом обсуждения во второй части являются возможности конструктивного описания многообразия решений $\Phi (A,b)$ линейной системы $Ax = b$, которые дает проекционный метод. Рассмотрены две формализации априорной информации вида “искомое решение ${{x}^{f}}$ похоже на известный вектор $\mu \in E$”.

В третьей части приведены два примера, демонстрирующие преимущества подхода, описанного во второй части, над методом регуляризации Тихонова [3] при решении двумерной задачи гравиразведки с использованием априорной информации.

ТЕОРИЯ

Исходное  пространство  $E$  предполагается $n$-мерным евклидовым относительно скалярного произведения (,), 1 – единичный оператор на $E$.

В линейной системе $Ax = b$ ($({{a}_{i}},x) = {{b}_{i}}$), i = 1, ..., m, $x \in E$ под $A$ одновременно понимается как совокупность векторов ${{a}_{i}}$ из $E$, так и матрица размера $m \times n$ с ${{a}_{i}}$ в качестве строк, $b = ({{b}_{i}}{\text{|}}_{1}^{m})$.

Для однородной системы $Ax = 0$ пространство решений $\Phi (A,0)$ в точности совпадает с ортогональным дополнением в $E$ к подпространству $L(A)$, порожденному $A$: $\Phi (A,0) = L{{(A)}^{ \bot }}$. Поэтому для решения системы $Ax = 0$ нужно конструктивно по $A$ построить ортопроектор $H(A)$: $E \to L{{(A)}^{ \bot }}$. В простейшем случае $A = (a)$ его явный вид дается следующей конструкцией:

Определение. Для $a \in E$ положим

По системе векторов $\{ {{a}_{i}}{\text{|}}_{1}^{m}\} $ построим в $E$ итеративно систему векторов $\{ {{\theta }_{i}}{\text{|}}_{1}^{m}\} $ и проекторов $\{ {{H}_{i}}{\text{|}}_{1}^{m}\} $ по следующей схеме:

Утверждение. Произведение ${{H}_{1}}{{H}_{2}} \ldots {{H}_{m}}$ является ортопроектором на $L{{({{a}_{1}}, \ldots ,{{a}_{m}})}^{ \bot }}$.

Таким образом, это произведение зависит только от $A$: ${{H}_{1}}{{H}_{2}} \ldots {{H}_{m}} = H(A)$ и осуществляет эффективную по $A$ параметризацию пространства решений $\Phi (A,0)$ однородной системы $Ax = 0$: для любого $s \in E$ образ $H(A)s \in \Phi (A,0)$.

Произвольное решение неоднородной системы $Ax = b$ есть сумма частного $x{\text{*}}$ и однородного, так что $\Phi (A,b) = x{\text{*}} + \Phi (A,0)$. Чтобы найти $x{\text{*}}$, выберем в $E$ ортобазис ${{e}_{1}}, \ldots ,{{e}_{n}}$ и запишем систему в координатном виде:

Введем дополнительную переменную ${{x}_{{n + 1}}}$ и свяжем с неоднородной системой $Ax = b$ расширенную однородную систему

Обозначим ее через $\{ A, - b\} {{x}_{e}} = 0$; x_e = (x₁, ..., x_n, ${{x}_{{n + 1}}})$. Если $x_{e}^{*}$ – решение расширенной системы и ${{x}_{{n + 1}}} = 1$, то $(x_{1}^{*}, \ldots ,x_{n}^{*})$ ∈ $\Phi (A,b)$. Следовательно, нужно найти параметр $s_{e}^{*} \in {{{\text{P}}}^{{n + 1}}}$, при котором решение $H(\{ A, - b\} )s_{e}^{*}$ системы $\{ A, - b\} {{x}_{e}} = 0$ в последней координате равно 1. В качестве $s_{e}^{*}$ можно взять вектор Мура-Пенроуза последней строки проектора $H(\{ A, - b\} )$: если $({{h}_{{ij}}})$, $i,j = 1, \ldots ,n + 1$ – координатное представление $H(\{ A, - b\} )$ и h_n + 1 = = $({{h}_{{n + 1j}}})$, $j = 1, \ldots ,n + 1$ – его последняя строка, то

Подведем итог: конструкция $H(A)$ полностью описывает многообразие $\Phi (A,b)$ решений неоднородной линейной системы $Ax = b$.

ВОЗМОЖНОСТИ ПРОЕКЦИОННОГО МЕТОДА

С математической точки зрения проекционный метод полностью и конструктивно решает линейные системы, но в реальности уравнение $Ax = b$ – это только часть целого комплекса условий, которым должно удовлетворять решение ${{x}^{f}}$. Если получится в координатах $x$ выразить какие-либо из оставшихся условий, то поиск искомого решения может быть продолжен на многообразии $\Phi (A,b)$ путем, например, оптимизации системы функционалов $\Phi = ({{F}_{1}}, \ldots ,{{F}_{k}})$, формализующих эти условия.

Предметом нашего рассмотрения будет дополнительное условие “искомое решение ${{x}^{f}}$ похоже на известный вектор $\mu \in E$”. Приведем две его возможные формализации.

1) Первая формализация: “${{x}^{f}}$ – ближайшая к $\mu $ точка на многообразии $\Phi (A,b)$”.

Если $x{\text{*}} + Hs$ – проекционная параметризация $\Phi (A,b)$, то поиск решения ${{x}^{f}}$ сводится к безусловной минимизации по $s$ на $E$ квадрата нормы ${{\left\| {x{\text{*}} + H - \mu } \right\|}^{2}}$, что, в свою очередь, приведет к линейной системе на искомый параметр ${{s}^{f}}$:

2) Вторая формализация более инвариантна относительно $\mu $ и в известной степени полукорреляционна: “${{x}^{f}}$ – ближайшая точка на $\Phi (A,b)$ к прямой $L(\mu )$, порожденной вектором $\mu $”.

В данном случае поиск ${{x}^{f}}$ сводится к безусловной минимизации по $s$ и $t$ на произведении $E \times {\text{R}}$ квадрата нормы ${{\left\| {x{\text{*}} + H - \mu t} \right\|}^{2}}$. Нужная пара параметров $({{s}^{f}},{{t}^{f}})$ получается как решение линейной системы

ПРИМЕРЫ

Будут рассмотрены два примера, в которых, в соответствие со схемами (4) и (5) формализации близости искомого решения ${{x}^{f}}$ к известному вектору $\mu $, сравниваются с классической тихоновской регуляризацией [2] относительно стабилизатора ${{\left\| {x - \mu } \right\|}^{2}}$.

Первая система выглядит так

В качестве $\mu $ берется нулевой вектор, так что в этом случае задача сводится к сравнению минимальных   по норме решений, найден-ных проекционным методом и методом Тихонова.

1) Проекционный метод (схема (4)):

2) Метод регуляризации Тихонова ($\alpha = 0.001$):

Видно, что полученные ответы не сильно отличаются по норме, но ${{x}^{f}}$ с большим правом является решением заданной системы.

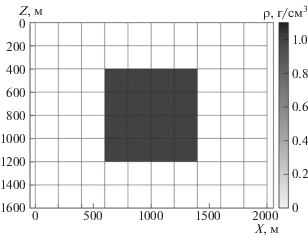
Второй пример связан с обратной задачей гравиразведки на двумерной модели с заданной сеткой плотностей $\rho $ (рис. 1).

Рис. 1.

Cетка плотностей.

В этом случае ${{x}_{j}}$ – неизвестная плотность в $j$-ой прямоугольной ячейке с вершинами $\sigma _{\nu }^{j}$, $\nu $ = 1, 2, 3, 4; ${{b}_{i}}$ – значение наблюденного поля в точке ${{s}_{i}}$ на поверхности; ${{a}_{{ij}}}$ – поле, порождаемое $j$-ой ячейкой в $i$-ой точке наблюдения. Имеем:

Для расчета решения прямой задачи гравиметрии в данной статье применяется теория функции комплексной переменной. Для расчета поля, порождаемого каждой ячейкой, использовалась формулы для многоугольника с постоянной плотностью [4].

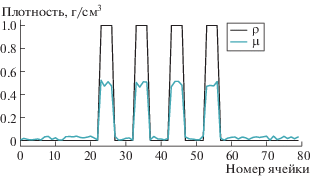
На рис. 2 показаны заданное распределение плотности $\rho $ и априорная информация $\mu $, которая равна немного зашумленной половине плотности.

Рис. 2.

Плотность исходной модели и априорная информация. Графическое представление показывает значение плотности в ячейке. Нумерация начинается в левом верхнем углу модели и идет непрерывно слева направо и сверху вниз.

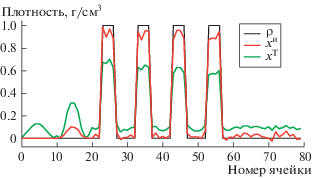
На рис. 3 показаны распределения плотностей ${{x}^{f}}$ и ${{x}^{t}}$, найденные соответственно с помощью проекционного метода (5) и метода регуляризации Тихонова с $\alpha = 0.03$. Выбор оптимального значения регуляризующего параметра был произведен итерационным методом “L-кривой”. Метод основан на выборе параметра регуляризации, представляющего хороший баланс между погрешностью и сложностью модели [5]. Видно, что, в то время как метод регуляризации Тихонова добавляет к априорной модели неинформативные фоновые значения, исследуемый метод использует априорную информацию с целью найти подобное решение на многообразии. Таким образом получается, что основная информация сконцентрирована там, где хотел бы ее видеть интерпретатор.

Рис. 3.

Сравнение решений с исходной моделью.

1) Оценка решения проекционным методом (схема (4)):

2) Оценка решения методом регуляризации Тихонова ($\alpha = 0.03$):

ЗАКЛЮЧЕНИЕ

Авторы предполагают дальнейшее применение проекционного метода для комплексирования геолого-геофизических данных в обратных задачах геофизики. На сегодняшний день результаты такого комплексирования являются, как правило, квазирешениями. Представляется, что проекционный метод позволит перейти от них к более точным решениям.