Доклады Российской академии наук. Науки о Земле, 2020, T. 493, № 1, стр. 103-106

Изучение процессов, протекающих в толще водной среды, по наблюдаемым на ее поверхности возмущениям представляет собой важную задачу, имеющую существенные практические приложения. При этом обратные задачи восстановления глубинных процессов по данным о вызываемых ими возмущениях морской поверхности, как правило, относятся к классу некорректно поставленных, их решение чувствительно к малым изменениям исходных данных [1]. Например, при обтекании точечного источника дебета Q, локализованного в точке (0, 0, –h), потоком идеальной жидкости, имеющим скорость V в положительном направлении оси Ox, на его свободной поверхности возникает волна [2]

где S = S(x, y) –отклонение свободной поверхности жидкости от ее равновесного положения z = 0, g – ускорение свободного падения. Даже в модельной постановке, при которой точно известно, что обтекается ровно один источник, восстановление его координат и дебета по известному полю отклонений свободной поверхности жидкости от ее равновесного положения S = S(x, y) на основе приведенных равенств представляет собой сложную задачу. Трудности существенно возрастают при обтекании тела реальной жидкостью, поскольку эквивалентная ему система гидродинамических особенностей заранее не известна. По этой причине подход к решению, даже плоской, обратной задачи генерации поверхностных волн [3] не дал удовлетворительных результатов при использовании данных лабораторных экспериментов [4] по измерению углов наклона поверхности воды, возмущаемой поперечно движущимися цилиндром и крыловым профилем.

Принципиально другое решение этой задачи, предложенное в [5], основано на методах машинного обучения [6–13]. При восстановлении параметров движущейся в толще воды модели по данным экспериментов [4] в качестве обучающей выборки использовались наборы измеренных значений тангенса угла наклона свободной поверхности жидкости в различных точках оси движения модели. Применение методов спектрального и статистического анализа, а также метода стохастического градиентного спуска позволило получить результаты в пределах погрешности 5%. Таким образом, методы машинного обучения показали свою эффективность при решении плоской задачи, поскольку данные опыта относились к поперечному обтеканию цилиндра и крылового профиля.

В настоящей работе методы машинного обучения применены к пространственной задаче восстановления параметров движущейся модели по измеренным возмущениям свободной поверхности жидкости. Обрабатывались данные опытов, которые проводились на экспериментальной установке, представляющей собой канал 300 × 50 × × 50 см, заполняемый водой [14]. В опытах наблюдались поверхностные волны, возникающие при горизонтальном движении в толще воды эллипсоида с длинами большой и малой осей, соответственно, 120 и 35 мм. Тангенс угла наклона возмущенной свободной поверхности воды к горизонту измерялся в вертикальной плоскости, проходящей через продольную ось симметрии модели в различных точках этой оси. Получены данные для 14 различных режимов движения эллипсоида на глубинах 66, 96 и 126 мм со скоростями от 265 до 838 мм/с.

Приведенные в таблицах [14] последовательности значений тангенса угла наклона поверхности жидкости для каждого режима движения были использованы в качестве обучающих выборок для определения глубины и скорости модели. Применялось обучение с учителем, то есть для каждого обучающего входного вектора имелся обучающий выходной вектор. Для этого была использована сеть прямого распространения сигнала типа многослойный персептрон, обучаемый алгоритмами, основанными на методе обратного распространения ошибки [6, 7]. В нашем случае обучающим множеством являлась последовательность значений тангенсов углов наклона свободной поверхности жидкости, измеренных в различных точках. Для выбора основных признаков такого множества, характеризующих изучаемые процессы, применяют сети глубокого обучения [11], но для этого, кроме большого объема исходной информации, требуются значительные вычислительные ресурсы или длительное время процесса обучения, что неприемлемо в реальных условиях и не отвечает требованиям оперативной обработки информации при определении параметров источника возмущения жидкости. Поэтому для выявления характерных признаков наблюдаемого процесса к выборкам данных, полученным в ходе эксперимента, а именно, к последовательности тангенсов углов наклона поверхности жидкости, измеренных в различных точках, было применено дискретное преобразование Фурье.

Известно, что спектр наблюдаемого сигнала инвариантен относительно смещения вдоль пространственной координаты. Это свойство позволило перейти от всей последовательности наблюдаемых координат обучающего вектора к нескольким линиям спектра, что значительно сократило размер нейронной сети и длительность процесса ее обучения. Более того, спектральный анализ с выделением главных компонент спектра устойчив к погрешностям наблюдений, а последующая аппроксимация их нейронной сетью, в соответствии с теоремой Колмогорова о представлении многомерных функций, устойчива, поскольку базируется на гладких монотонных функциях, что позволяет решить проблему корректности и устойчивости поставленной задачи.

На рис. 1 в качестве примеров приведены полученные с помощью дискретного преобразования Фурье и пакета Wolfram Mathematica спектры последовательностей тангенсов угла наклона поверхности воды, умноженных на 10⁴, для двух режимов движения эллипсоида. По горизонтальным осям отложены номера гармоник n, по вертикальным – модули их комплексных амплитуд s. Для большей наглядности точки графиков соединены отрезками прямых. Первый режим (верхний график) соответствует глубине H = 96 мм и скорости V = 450 мм/ с, второй (нижний график) – H = 66 мм, V = 424 мм/с.

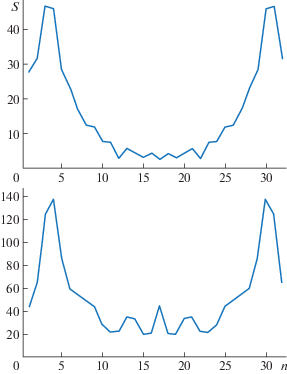
Как видно, в результате спектрального анализа полученных экспериментальным путем последовательностей значений тангенсов углов наклона поверхности воды выделены две основные частоты спектра, различные по амплитуде для всех серий проводившихся лабораторных экспериментов. Статистический анализ выборки этих амплитуд линий спектра выявил сильную корреляцию между ними и характеристиками источников возмущений. Поэтому для обучения нейронной сети были использованы вычисленные параметры обучающего вектора с двумя координатами, имеющими значения основных амплитуд спектра.

После проведения достаточного количества численных экспериментов была выбрана архитектура нейронной сети. Во входном слое имеется 2 нейрона (вершины), на которые в процессе обучения и применения подаются значения амплитуд выбранных спектральных линий. В первом (скрытом) слое имеется некоторое количество (от 20 до 70 в зависимости от эксперимента) нейронов с активационной функцией гиперболический тангенс, каждый из которых соединен синапсом (ребром) с каждым нейроном из входного слоя и с каждым из двух нейронов выходного слоя. Такую сеть принято представлять следующим образом: 2–50–2. Это означает, что сеть имеет 2 входных, 50 скрытых и 2 выходных нейрона.

Для исключения переобучения сети и придания ей свойства обобщения из исходных данных была сформирована выборка большего объема путем 5%-го зашумления с плотностью равномерного распределения. Наилучший интервал зашумления был выявлен в результате вычислительного эксперимента. Для обучения нейронной сети по вариативности факторов проведено нормирование данных, то есть, приведение к относительным единицам в интервале (0, 1) путем деления каждого параметра на максимальное значение. Обучение нейронной сети проводилось путем минимизации функции ошибки и корректировки весовых коэффициентов синаптических связей между нейронами по среднеквадратичной ошибке между расчетными и наблюдаемыми данными.

Классический метод градиентного спуска основан на выборе величины весов связей между нейронами для достижения минимальной ошибки аппроксимации целевой функции за минимальное число шагов обучения. Недостаток данного метода состоит в том, что в некоторых случаях процесс минимизации не сходится к глобальному значению, т.е. “застревает” в локальном минимуме. Эта проблема решена путем использования метода стохастического градиентного спуска [12, 13]. Особенности такого подхода состоят в том, что он помогает избежать “застревания” модели в точке локального минимума, проще и эффективнее в вычислениях. Численные эксперименты с нейронной сетью подтвердили совпадение их результатов с данными лабораторных экспериментов с погрешностью в пределах 7%.

Методы машинного обучения показали свою эффективность при решении как плоской, так и пространственной задачи определения параметров движущихся в жидкости моделей по создаваемым ими возмущениям свободной поверхности жидкости. Применение описанных подходов к другим некорректно поставленным задачам механики жидкости и геофизики представляет собой практически значимую задачу и требует дальнейшего изучения.