Доклады Российской академии наук. Науки о Земле, 2021, T. 497, № 2, стр. 189-192

Адекватная информация о текущем и ожидаемом качестве воды необходима для повышения эффективности использования водных ресурсов. Трудности ее получения связаны с тем, что процессы загрязнения и самоочищения индивидуальны для каждого водного объекта и его отдельных створов. Однако существуют некоторые общие динамические закономерности формирования состава и свойств воды, на что указывает их пространственно-временная вариабельность, наблюдаемая во всех случаях. Это неочевидно при “линейном подходе” [3] к формированию случайных по своей природе показателей, так как природные гидросистемы отличаются существенной нелинейностью [8].

Для демонстрации этого удобно перейти к оценке безразмерной (относительной) концентрации загрязнения $u$, принимая эту величину равной 1 и 0, соответственно, при максимальном и минимальном значениях достаточно представительного временного ряда. Средний квадрат случайного смещения концентрации в течение n шагов продолжительности Δt есть $\overline {u_{{n\Delta t}}^{2}} $ = = $\overline {{{{(\sum\nolimits_{i = 1}^n {{{x}_{{i\Delta t}}}} )}}^{2}}} $ = $\sum\nolimits_{i = 1}^n {\overline {x_{{i\Delta t}}^{2}} } $ + 2$\sum\nolimits_{j > i}^n {\overline {{{x}_{{j\Delta t}}}{{x}_{{i\Delta t}}}} } $ (i, j – номер шага), поскольку осредненное значение произведения независимых случайных величин равно произведению средних, при этом сумма перекрестных членов обращается в нуль вследствие симметричности и независимости шагов в рядах $i \ne j$: $\sum\nolimits_{j > i}^n {\overline {{{x}_{j}}{{x}_{i}}} } $ = $\sum\nolimits_{j > i}^n {{{{\bar {x}}}_{j}}{{{\bar {x}}}_{i}}} $ = 0, а квадрат единичного смещения за интервал времени от t до t + Δt равен $\overline {x_{t}^{2}} $ = 0.5(+1)² + 0.5(–1)² = 1. Отсюда: $\overline {u_{{n\Delta t}}^{2}} $ = = $\sum\nolimits_{i = 1}^n {\overline {x_{{i\Delta t}}^{2}} } $ = n, т.е. смещение концентрации возрастает по параболическому закону.

Этот вывод распространяется на широкий класс случайных процессов, однако здесь требует уточнения, так как “блуждание” концентрации отличается от блуждания броуновских частиц. В последнем случае при $n \to \infty $ также и $u_{{n\Delta t}}^{2} \to \infty $, в то время как “поток” концентрации через их максимальное и минимальное значение (здесь, соответственно, 1 и 0) равен нулю, т.е. ${{u}_{{n{{\Delta }}t}}}$ = = $\sum\nolimits_{i = 1}^n {\Delta {{x}_{{i{{\Delta }}t}}}} $ = 0. Поэтому неверно принимать, что ${{u}_{{t + \Delta t}}}$ зависит исключительно от $u_{t}^{2}$. Вместо этого нами сформирована суперпозиция нелинейного и линейного законов движения так, чтобы полная функция ${{u}_{{t + \Delta t}}}$ = $f(u_{t}^{2},~{{u}_{t}})$ была параболой, пересекающей ось абсцисс при ${{u}_{t}} = 1$ и ${{u}_{t}} = 0$. Такова нелинейная логистическая зависимость ${{u}_{{t + {{\Delta }}t}}}$ = = ${{\mu }}{{u}_{t}}\left( {1 - {{u}_{t}}} \right)$, где параметр пропорциональности µ характеризует интенсивность динамики переноса загрязняющих веществ.

Полученное выражение позволяет проследить изменение концентрации загрязнителя от ее измеренного в момент t значения u_t неограниченно долго путем выполнения необходимого числа шагов.

Влияние качества воды на коэффициент μ проиллюстрируем анализом результатов измерений концентрации меди и взвешенных веществ в р. Исети, створ г. Екатеринбург в 2008–2010 гг. На основе экспериментальных данных на рис. 1 приведена функция ${{u}_{{t + \left( {i + 1} \right){{\Delta }}t}}}$ = $f\left( {{{u}_{{t + i{{\Delta }}t}}}} \right)$ при i = 0, …, 3 и при полученных из эксперимента среднеарифметических значениях коэффициентов μ = = 1.7 для меди и 2.3 для взвешенных веществ.

Рис. 1.

Увеличенные в 25 раз верхние части логистического отображения динамики концентрации меди (а, слева) и взвешенных веществ (б, справа) в воде после 1-го (пунктирная линия), 2-го (штриховая), 3-го (штрих-пунктирная) и 4-го (сплошная) шагов.

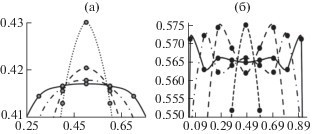
Выяснилось, что при достаточном числе шагов концентрация, какой бы она ни оказалась в момент t проведения наблюдений, в обоих рассмотренных случаях приближается к некоторому устойчивому (равновесному) значению. Впрочем, заметны отличия поведения концентрации выбранных веществ в зависимости от значения µ: из рис. 1а следует, что концентрация меди последовательно стремится к своему устойчивому состоянию. Например, при ее начальной концентрации в воде 0.5 она снижается в ряду: 0.430; 0.420; 0.418; 0,417. В противоположность этому на рис. 1б концентрация взвешенного вещества испытывает небольшие циклические колебания; например, при начальной концентрации 0.5: 0.575; 0.562; 0.566; 0.565. При этом амплитуда колебаний сокращается в ряду: +0.013; –0.004; +0.001… Затухание колебаний происходит резче при начальной концентрации вещества 0.3 или 0.7, где после перечисленных шагов концентрация уже составляет 0.483; 0.574; 0.562; 0.566 соответственно, а амплитуда колебаний +0.91; –0.12; +0.04…

В рассмотренных примерах значение величины Δt зависит от того, как быстро перестраиваются частицы растворенного в воде вещества, т.е. от скорости их броуновского блуждания. Обычно коэффициент диффузии здесь D ~ 10^–6 см²/с, поэтому при низких концентрациях, когда межчастичные расстояния достигают h = 0.1 см, такое время по формуле Эйнштейна $t\sim \frac{{{{h}^{2}}}}{D}\sim 3$ ч. В реальных условиях величина h и время стабилизации концентрации значительно меньше, а потому пользователи, скорее всего, могут оценить лишь устойчивое значение концентраций, формирующееся практически немедленно. Впрочем, ниже показано, что последнее заключение справедливо не всегда, а только в случае сравнительно низких значений µ, использованных в примерах.

Значения коэффициента µ, как и концентрация загрязнений воды, характеризуются большим разбросом. В вышеприведенном случае рассчитанные среднеквадратические отклонения µ составляют 2.5 для меди и 2.3 для взвешенных веществ. Поэтому целесообразно рассмотреть качество воды не только при его среднеарифметических значениях µ, но и в случае ${{\mu }} \in \left[ {0,~~4} \right]$.

В соответствии с логистическим уравнением $~{{u}_{{t + \left( {i + 1} \right) \cdot {{\Delta }}t}}} = f\left( {{{u}_{{t + i \cdot {{\Delta }}t}}}} \right)$ при μ ≤ 1 с течением времени происходит постепенное понижение показателей качества воды, т.е. самоочищение преобладает над загрязнением при любых начальных значениях u. Если ${{\mu }} \in [1,2]$, то формируется равновесный уровень качества воды, например, для μ = 2 при u = 0.5. Наиболее интересные эффекты нелинейности возникают при µ > 2. Здесь уровень загрязнения воды начинает испытывать циклические колебания, что заметно уже на рис. 1б. Анализ показывает, что при 2 < µ < 3 колебания являются затухающими, при µ = 3 они становятся постоянными, а при µ > 3 амплитуда колебаний возрастает на каждом последующем шагу (рис. 2). Так нелинейная система реагирует на возрастание загрязнения.

Рис. 2.

Логистические отображения динамики качества воды при μ = 3 (а) и при μ = 4 (б): функция u_iΔt при i = 0, …, 3, расшифровка линий как на рис. 1.

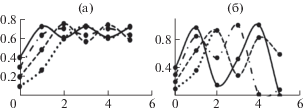
Анализ приведенной ранее логистической функции ${{u}_{{t + \left( {i + 1} \right){{\Delta }}t}}}$ = $f\left( {{{u}_{{t + i{{\Delta }}t}}}} \right)$ также свидетельствует о том, что при µ = 3 в системе происходит раздвоение (бифуркация [8]) устойчивых значений концентрации загрязнения, и дополнительное раздвоение – при µ = 4. Если же µ > 4, то возникают все новые бифуркации. Каскад следующих друг за другом бифуркаций вводит систему в непредсказуемый режим вплоть до формирования абсолютно хаотичного изменения качества воды.

Эффекты циклического и хаотического изменения показателей состава воды весьма распространены, они упоминаются даже в официальных отчетах [1, 2, 4]. Так, в [1] отмечено, что загрязнение подземных вод мышьяком, бериллием и ртутью “порой носит периодический характер”. В [4] то же установлено для поверхностных вод Куйбышевского и Саратовского водохранилищ. В [2] записано: “…Молдова, Румыния и Украина сталкиваются с большими непрогнозируемыми деструктивными явлениями на наших реках”, это указывает на хаотическое изменение качества воды в условиях ее интенсивного загрязнения. Что же касается собственно эффектов нелинейности, то явным доказательством их существования является расслоение примеси [7], а также фрактальность временных рядов состава воды [6].

Приведенные результаты позволяют судить о динамике формирования состава и свойств воды путем оценки µ. Так, если вариабельность концентрации невелика, то μ = $\frac{{{{u}_{{t + \Delta t}}}}}{{{{u}_{t}}\left( {1 - {{u}_{t}}} \right)}}$ < 2, а устойчивое значение концентрации u_t < 0.5. В отличие от этого при высокой вариабельности, например, когда через каждый интервал Δt качество воды колеблется между 0.1 и 0.9, имеем μ = $\frac{1}{2}\left( {\frac{{0.9}}{{0.1\left( {1 - 0.1} \right)}}} \right.$ + + $\left. {\frac{{0.1}}{{0.9\left( {1 - 0.9} \right)}}} \right)$ ≈ 5.5, и наступает хаос. Последней ситуации следует по возможности избегать, например, предотвращая залповые сбросы загрязняющих веществ предприятиями.

Если обнаружится, что какие-то эффекты циклического или хаотического изменения состава природной воды плохо отображаются предложенным уравнением ${{u}_{{t + \left( {i + 1} \right){{\Delta }}t}}}$ = $f\left( {{{u}_{{t + i{{\Delta }}t}}}} \right)$, то следует искать другую логистическую функцию, пригодную для такого описания, – известен широкий класс таких функций (как правило, с квадратичным максимумом в интервале [0, 1]). В частности, периодические циклы, бифуркации и переходы к абсолютному хаосу описываются функциями ${{x}_{{i + 1}}}$ = ${{\mu }}{{x}_{i}}\exp \left( { - {{x}_{i}}} \right)$, ${{x}_{{i + 1}}}$ = ${{\mu }}{{x}_{i}}{\text{/(}}1 + x_{i}^{3}{\text{)}}$, ${{x}_{{i + 1}}}$ = ${{\mu }}{{x}_{i}}{\text{/}}(1 + x_{i}^{4})$.

Отметим, что в рамках общенаучных представлений влияющими факторами нелинейности природных вод выступают флуктуации параметров порядка, определяющие сингулярные вклады в контролируемые динамические характеристики [5]. Таковы эффекты, показывающие, что вопреки действию закона возрастания энтропии природа демонстрирует заметную степень организованности.