Доклады Российской академии наук. Науки о Земле, 2021, T. 500, № 1, стр. 53-57

О неустойчивых изостатических стратификациях тяжелых геомассивов

Е. И. Рыжак^1, *, С. В. Синюхина¹

¹ Институт физики Земли им. О.Ю. Шмидта Российской академии наук
Москва, Россия

Поступила в редакцию 28.05.2021
После доработки 29.05.2021
Принята к публикации 31.05.2021

DOI: 10.31857/S2686739721090164

Аннотация

В работе аналитически исследуются условия возникновения неустойчивости стратифицированных тяжелых геомассивов. Считается, что геоматериал, образующий геомассив, является упругим и обладает как объемной, так и сдвиговой жесткостью. Невозмущенное равновесное состояние геомассива является изостатическим, т.е. характеризуется гидростатическим полем напряжений. Стратификация плотности и упругих свойств геоматериала по глубине считается непрерывной. Получены характеристики таких стратификаций упругих и плотностных параметров, которые заведомо приводят к возникновению неустойчивости. Полученные достаточные условия неустойчивости сопоставлены с полученными ранее авторами достаточными условиями устойчивости. Рассмотрены возможные геофизические приложения результатов.

Ключевые слова: тяжелые стратифицированные геомассивы, изостатическое равновесное состояние, упругие геоматериалы, устойчивость, неустойчивость

1. ВВЕДЕНИЕ

При исследовании вопросов устойчивости тяжелых стратифицированных геомассивов существенным упрощающим предположением является предположение об объемной упругости (и, следовательно, нулевой сдвиговой жесткости) геоматериала, образующего геомассив. В рамках этого достаточно традиционного предположения Е.И. Рыжаком с соавторами ранее [1–3] был получен исчерпывающий результат в виде необходимого и достаточного условия устойчивости, устанавливающего критическую (положительную) скорость нарастания плотности с глубиной, зависящую от сжимаемости геоматериала. Однако реальные геоматериалы не являются объемно-упругими: они обладают значительной сдвиговой жесткостью, что проявляется, в частности, в существовании не только продольных, но и поперечных сейсмических волн. Очевидно, что ненулевая сдвиговая жесткость увеличивает устойчивость геомассива по сравнению со случаем чисто объемной упругости. Выяснение степени влияния сдвиговой жесткости на устойчивость стратифицированных геомассивов представляет интерес как с чисто теоретической, так и с прикладной точки зрения.

Наличие сдвиговой жесткости существенно усложняет анализ устойчивости, и получение идеального результата в виде необходимого и достаточного условия устойчивости пока не представляется возможным. В этой связи становится актуальным получение отличных друг от друга достаточного и необходимого условий устойчивости. В работе Е.И. Рыжака и С.В. Синюхиной [4] при некоторых дополнительных предположениях о характере плотностной стратификации было получено достаточное условие устойчивости, не являющееся необходимым.

Целью настоящей работы является получение необходимого условия устойчивости, что эквивалентно получению достаточного условия неустойчивости (в силу того, что последнее есть не что иное, как нарушение первого). С прикладной точки зрения знание условий заведомого возникновения неустойчивости не менее важно, чем знание условий заведомой устойчивости.

Важной и неотъемлемой частью работы является сопоставление упомянутых условий друг с другом и с полученными ранее условиями для объемно-упругих геоматериалов, что создает единую картину явления и позволяет судить о поведении геосистем в зависимости от изменения их параметров в ходе тех или иных геопроцессов. В частности, выявляется стабилизирующее влияние сдвиговых жесткостей, а также появляется возможность предсказания потери устойчивости (которая может иметь катастрофические последствия) при их уменьшении. Помимо этого, появляется возможность оценки достоверности существующих представлений о характере плотностной и жесткостной стратификации реальных геомассивов с точки зрения соответствия этих представлений условиям устойчивости.

2. ИССЛЕДУЕМЫЙ КЛАСС ГЕОМАССИВОВ

В данной работе рассматривается тот же класс тяжелых стратифицированных геомассивов, что и в работе [4] (но при этом сформулированная во введении цель работы – иная). Опишем этот класс.

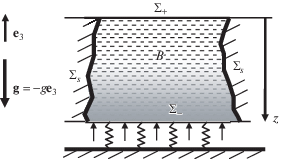
Зададим ортонормированный базис $\left( {{{{\mathbf{e}}}_{1}},\,{{{\mathbf{e}}}_{2}},\,{{{\mathbf{e}}}_{3}}} \right)$, причем орт ${{{\mathbf{e}}}_{3}}$ направлен вертикально вверх (рис. 1). Будем считать, что изучаемый геомассив находится в однородном поле силы тяжести, направленном вертикально вниз (${\mathbf{g}} = - g{{{\mathbf{e}}}_{3}}$) и состоит из непрерывно стратифицированного по глубине твердого упругого геоматериала, занимающего в исследуемом на устойчивость равновесном состоянии область $B$, представляющую собой некоторую ограниченную подобласть горизонтального плоского слоя. Верхняя граница области ${{\Sigma }_{ + }}$ (находящаяся на верхней граничной плоскости слоя) предполагается свободной, а боковые границы ${{\Sigma }_{s}}$ (расположенные в толще слоя) считаются жестко закрепленными. На нижней границе области ${{\Sigma }_{ - }}$ (расположенной на нижней граничной плоскости слоя) ставится силовое граничное условие, а именно: предполагается, что граничные усилия представляют собой комбинацию постоянного давления (равного равновесному давлению в нижней части слоя) и усилия, порождаемого упругой заделкой некоторой конечной жесткости (рис. 1). Силовое граничное условие на нижней границе призвано моделировать реакцию подстилающих слоев. Дополнительно введем вертикальную координату $z$ (отсчетную глубину), нулевое значение которой соответствует свободной поверхности ${{\Sigma }_{ + }}$ (рис. 1).

Рис. 1.

Исследуемый геомассив.

Несмотря на то что геоматериал считается твердым (т.е. имеющим ненулевую сдвиговую жесткость), невозмущенное равновесное поле напряжений предполагается гидростатическим (иными словами, имеет место изостазия). Данное предположение не противоречит тому, что инкрементальный отклик материала характеризуется ненулевыми модулями сдвига. По сути, это предположение о процессах, в результате которых сформировалось то состояние, устойчивость которого исследуется. Геоматериал в процессе формирования равновесного состояния мог иметь совершенно другие свойства (например, это мог быть расплав, в дальнейшем застывший и превратившийся в твердый упругий материал). Заметим, что в геофизике предположение об изостазии, т.е. гидростатичности равновесного поля напряжений, является традиционным.

3. КРИТЕРИИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ. ВЫВОД ДОСТАТОЧНОГО УСЛОВИЯ НЕУСТОЙЧИВОСТИ

Исследование устойчивости и неустойчивости в малом будет основано на известных энергетических критериях [5–7].

Критерием устойчивости является неотрицательность квадратичного функционала второй вариации полной потенциальной энергии (ППЭ) на кинематически допустимых полях малых смещений по отношению к исследуемому на устойчивость равновесному состоянию системы [5–7]. Критерием неустойчивости является существование таких кинематически допустимых полей малых смещений, на которых вторая вариация ППЭ отрицательна.

При анализе устойчивости будет использоваться отсчетное описание сплошной среды, причем исследуемое на устойчивость равновесное состояние принимается за отсчетную конфигурацию. Обозначения механических величин близки к обозначениям книг [8, 9], но с использованием системы Гиббса безындексных обозначений тензорных величин.

Пусть ${\mathbf{x}}$ – радиус-вектор материальной точки в отсчетной конфигурации. Запишем радиус-вектор ${\mathbf{r}}$ ее текущего положения в следующем виде: ${\mathbf{r}} = {\mathbf{r}}({\mathbf{x}})$.

В силу гидростатичности невозмущенного отсчетного равновесного состояния плотность и давление в этом состоянии стратифицированы по глубине $z$:

(3.1)

${{\rho }_{\kappa }} = {{\rho }_{\kappa }}(z),\quad {{p}_{\kappa }} = {{p}_{\kappa }}(z),\quad \frac{{d{{p}_{\kappa }}}}{{dz}} = {{\rho }_{\kappa }}(z)g.$

Предполагается, что упругие модули геоматериала (задающие инкрементальное определяющее соотношение) также стратифицированы по глубине.

Инкрементальный упругий закон для напряжений Пиолы относительно гидростатического исходного состояния [8, 9], имеет следующий вид:

(3.2)

$\begin{gathered} \delta {{{\mathbf{T}}}_{\kappa }}({\mathbf{x}}) = {\mathbf{L}}(z):\delta {\mathbf{\varepsilon }} - {{p}_{\kappa }}(z){\mathbf{I}}({\mathbf{I}}:{{\nabla }_{\kappa }} \otimes \delta {\mathbf{r}}) + \\ + \;{{p}_{\kappa }}(z){{\nabla }_{\kappa }} \otimes \delta {{{\mathbf{r}}}^{T}}, \\ \delta {\mathbf{r}}({\mathbf{x}},t) \equiv {\mathbf{r}}({\mathbf{x}},t) - {\mathbf{x}}, \\ \delta {\mathbf{\varepsilon }} = \frac{1}{2}({{\nabla }_{\kappa }} \otimes \delta {\mathbf{r}} + {{\nabla }_{\kappa }} \otimes \delta {{{\mathbf{r}}}^{T}}), \\ \end{gathered} $

где ${\mathbf{I}}$ – единичный тензор второго ранга (ТР(2)). Инкрементальное соотношение для напряжений Коши (выражающее жесткостные свойства материала) задает тензор упругих модулей ${\mathbf{L}}(z)$ (являющийся тензором четвертого ранга (ТР(4)); он симметричен в силу существования упругого потенциала и гидростатичности начальных напряжений. Дополнительно предполагается, что ${\mathbf{L}}(z)$ таков, что чисто объемные инкрементальные деформации порождают гидростатические инкрементальные напряжения Коши. Из этого вытекает, что девиаторные инкрементальные деформации порождают девиаторные инкрементальные напряжения Коши и, в силу спектральной теоремы, ${\mathbf{L}}(z)$ имеет следующий вид [10]:

(3.3)

$\begin{gathered} {\mathbf{L}}(z) = \sum\limits_{i = 1}^5 {2{{G}_{i}}(z){{{\mathbf{\Gamma }}}_{i}}(z)} \otimes {{{\mathbf{\Gamma }}}_{i}}(z) + K(z){\mathbf{I}} \otimes {\mathbf{I}}, \\ {{{\mathbf{\Gamma }}}_{i}}(z):{\mathbf{I}} = 0,\quad {{{\mathbf{\Gamma }}}_{i}}(z):{{{\mathbf{\Gamma }}}_{j}}(z) = {{\delta }_{{ij}}}, \\ \end{gathered} $

где $K(z)$ – модуль объемного сжатия, ${{G}_{i}}(z)$ – модули, соответствующие девиаторным деформациям, ${{{\mathbf{\Gamma }}}_{i}}(z)$ – нормированные собственные девиаторы.

Пусть симметричный положительно определенный ТР(2) ${\mathbf{S}}$ задает жесткость упругой заделки на ${{\Sigma }_{ - }}$. Вторая вариация ППЭ $R\left\{ {\delta {\mathbf{r}}} \right\}$ принимает следующий вид, вытекающий из результатов работ [2, 3]:

(3.4)

$\begin{gathered} R\left\{ {\delta {\mathbf{r}}} \right\} = \left\langle {\mathop {\delta {\mathbf{\varepsilon }}:{\mathbf{L}}:\delta {\mathbf{\varepsilon }} - 2{{\rho }_{\kappa }}g({{\nabla }_{\kappa }} \cdot \delta {\mathbf{r}})(\delta {\mathbf{r}} \cdot {{{\mathbf{e}}}_{3}}) + }\limits_{} } \right. \\ + \;{{\left. {\frac{{d{{\rho }_{\kappa }}}}{{dz}}g{{{(\delta {\mathbf{r}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{B}} + {{\left\langle {{{\rho }_{\kappa }}g{{{(\delta {\mathbf{r}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{{{{\Sigma }_{ + }}}}} - \\ - \;{{\left\langle {{{\rho }_{\kappa }}g{{{(\delta {\mathbf{r}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{{{{\Sigma }_{ - }}}}} + {{\left\langle {\delta {\mathbf{r}} \cdot {\mathbf{S}} \cdot \delta {\mathbf{r}}} \right\rangle }_{{{{\Sigma }_{ - }}}}}, \\ \end{gathered} $

где угловые скобки обозначают интегрирование по отсчетному множеству, указанному справа внизу.

Выведем неравенство, выражающее необходимое условие устойчивости. Пусть поле $\delta {{{\mathbf{r}}}_{*}}({\mathbf{x}})$ является некоторым кинематически допустимым полем инкрементальных смещений, и пусть функционал $\bar {R}\left\{ {\delta {\mathbf{r}}} \right\}$ таков, что

$\bar {R}\left\{ {\delta {{{\mathbf{r}}}_{*}}} \right\} \geqslant R\left\{ {\delta {{{\mathbf{r}}}_{*}}} \right\}.$

Тогда неравенство

(3.5)

$\bar {R}\left\{ {\delta {{{\mathbf{r}}}_{*}}} \right\} \geqslant 0$

является необходимым условием устойчивости.

Конкретизируем величины, входящие в сформулированное условие. Построим функционал $\bar {R}\left\{ {\delta {\mathbf{r}}} \right\}$. Пусть $\Omega \subset B$ и ${{\left. {\delta {{{\mathbf{r}}}_{*}}} \right|}_{{B\backslash \Omega }}} \equiv 0$. Определим $\bar {G}$ равенством

(3.6)

$\bar {G} = \mathop {\max }\limits_\Omega (\mathop {\max }\limits_i ({{G}_{i}}(z))).$

Тогда, вводя ТР(4) ${{{\mathbf{1}}}^{{{\text{dev}}}}}$ (ортогональный проектор на подпространство симметричных девиаторов), получим следующее неравенство:

(3.7)

$2\bar {G}\delta {\mathbf{\varepsilon }}:{{{\mathbf{1}}}^{{{\text{dev}}}}}:\delta {\mathbf{\varepsilon }} + K(z){{(\delta {\mathbf{\varepsilon }}:{\mathbf{I}})}^{2}} \geqslant \delta {\mathbf{\varepsilon }}:{\mathbf{L}}(z):\delta {\mathbf{\varepsilon }}.$

Подставляя левую часть неравенства (3.7) в выражение (3.4), учитывая, что $\delta {\mathbf{\varepsilon }}:{\mathbf{I}} = {{\nabla }_{\kappa }} \cdot \delta {\mathbf{r}}$ и выделяя квадрат суммы, получим:

(3.8)

$\begin{gathered} \bar {R}\left\{ {\delta {{{\mathbf{r}}}_{*}}} \right\} \equiv \left\langle {\mathop {2\bar {G}\delta {{{\mathbf{\varepsilon }}}_{*}}:{{{\mathbf{1}}}^{{{\text{dev}}}}}:}\limits_{} \delta {{{\mathbf{\varepsilon }}}_{*}} + } \right. \\ + \;K{{\left( {{{\nabla }_{\kappa }} \cdot \delta {{{\mathbf{r}}}_{*}} - \frac{{{{\rho }_{\kappa }}g}}{K}\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}}} \right)}^{2}} + \\ + \;{{\left. {\left( {\frac{{d{{\rho }_{\kappa }}}}{{dz}} - \frac{{{{\rho }_{\kappa }}^{2}g}}{K}} \right)g{{{(\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{\Omega }}. \\ \end{gathered} $

Необходимое условие устойчивости примет следующий вид:

(3.9)

$\begin{gathered} 2\bar {G}{{\left\langle {\delta {{{\mathbf{\varepsilon }}}_{*}}:{{{\mathbf{1}}}^{{{\text{dev}}}}}:\delta {{{\mathbf{\varepsilon }}}_{*}}} \right\rangle }_{\Omega }} + \\ + \;{{\left\langle {K{{{({{\nabla }_{\kappa }} \cdot \delta {{{\mathbf{r}}}_{*}} - \frac{{{{\rho }_{\kappa }}g}}{K}\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{\Omega }} \geqslant \\ \geqslant \;{{\left\langle {\left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right)g{{{(\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{\Omega }}. \\ \end{gathered} $

Заметим, что если величина $\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}$ неположительна во всей области $B$, то система заведомо устойчива, и поиск необходимого условия устойчивости не имеет смысла. Поэтому будем рассматривать случай, когда на некоторой замкнутой подобласти эта величина строго положительна, что равносильно неравенству

(3.10)

$\mathop {\max }\limits_B \left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right) > 0.$

В силу предположения о непрерывности распределений ${{\rho }_{\kappa }}(z)$ и $K(z)$, а также о кусочной гладкости ${{\rho }_{\kappa }}(z)$, существует подобласть, на которой минимум этой величины не меньше, чем половина максимума; именно эту подобласть примем за область $\Omega $:

(3.11)

$\mathop {\min }\limits_\Omega \left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right) \geqslant \frac{1}{2}\mathop {\max }\limits_B \left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right).$

Тогда следствием неравенства (3.9) будет неравенство

(3.12)

$\begin{gathered} 2\bar {G}{{\left\langle {\delta {{{\mathbf{\varepsilon }}}_{*}}:{{{\mathbf{1}}}^{{{\text{dev}}}}}:\delta {{{\mathbf{\varepsilon }}}_{*}}} \right\rangle }_{\Omega }} + \\ + \;{{\left\langle {K{{{({{\nabla }_{\kappa }} \cdot \delta {{{\mathbf{r}}}_{*}} - \frac{{{{\rho }_{\kappa }}g}}{K}\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{\Omega }} \geqslant \\ \geqslant \frac{1}{2}\mathop {\max }\limits_B \left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right)g{{\left\langle {{{{(\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{\Omega }}. \\ \end{gathered} $

Для полей, обращающихся в нуль на границе области, справедлива известная формула Кельвина [11], в силу которой

(3.13)

$\begin{gathered} 2\bar {G}{{\left\langle {\delta {{{\mathbf{\varepsilon }}}_{*}}:{{{\mathbf{1}}}^{{{\text{dev}}}}}:\delta {{{\mathbf{\varepsilon }}}_{*}}} \right\rangle }_{\Omega }} = \\ = \bar {G}{{\left\langle {{{{\left| {{{\nabla }_{\kappa }} \times \delta {{{\mathbf{r}}}_{*}}} \right|}}^{2}}} \right\rangle }_{\Omega }} + \frac{4}{3}\bar {G}{{\left\langle {{{{({{\nabla }_{\kappa }} \cdot \delta {{{\mathbf{r}}}_{*}})}}^{2}}} \right\rangle }_{\Omega }}. \\ \end{gathered} $

Потребуем, чтобы поле $\delta {{{\mathbf{r}}}_{*}}({\mathbf{x}})$ дополнительно удовлетворяло равенству

(3.14)

$\begin{gathered} {{\nabla }_{\kappa }} \cdot \delta {{{\mathbf{r}}}_{*}} = \frac{{{{\rho }_{\kappa }}g}}{K}\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}} \Rightarrow \\ \Rightarrow {{({{\nabla }_{\kappa }} \cdot \delta {{{\mathbf{r}}}_{*}})}^{2}} \leqslant \mathop {\max }\limits_\Omega \left( {\frac{{\rho _{\kappa }^{2}{{g}^{2}}}}{{{{K}^{2}}}}} \right){{(\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}^{2}}. \\ \end{gathered} $

Такие поля существуют; в частности, таким является поле

(3.15)

$\begin{gathered} \delta {{{\mathbf{r}}}_{*}}({\mathbf{x}}) = \nabla f \times {{{\mathbf{e}}}_{2}} + \frac{{{{\rho }_{\kappa }}g}}{K}f{{{\mathbf{e}}}_{1}}, \\ {{\left. f \right|}_{{\partial \Omega }}} = 0,\quad {{\nabla }_{\kappa }}f \times {{\left. {{{{\mathbf{e}}}_{2}}} \right|}_{{\partial \Omega }}} = 0. \\ \end{gathered} $

Учитывая (3.13) и (3.14), деля затем обе части неравенства (3.12) на положительную величину $\frac{1}{2}g{{\left\langle {{{{(\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }_{\Omega }}$, получим окончательно необходимое условие устойчивости в следующем виде:

(3.16)

$\bar {G} \geqslant \frac{{\mathop {\max }\limits_B \left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right)}}{{\frac{2}{g}\left( {\frac{{{{{\left\langle {{{{\left| {{{\nabla }_{\kappa }} \times \delta {{{\mathbf{r}}}_{*}}} \right|}}^{2}}} \right\rangle }}_{\Omega }}}}{{{{{\left\langle {{{{(\delta {{{\mathbf{r}}}_{*}} \cdot {{{\mathbf{e}}}_{3}})}}^{2}}} \right\rangle }}_{\Omega }}}} + \frac{4}{3}\mathop {\max }\limits_\Omega {{{\left( {\frac{{{{\rho }_{\kappa }}g}}{K}} \right)}}^{2}}} \right)}}.$

В работе [4] были получены следующие достаточные условия устойчивости рассматриваемой системы:

(3.17)

$\begin{gathered} \frac{{d{{\rho }_{\kappa }}}}{{dz}}(z) - \frac{{{{{({{\rho }_{\kappa }}(z))}}^{2}}g}}{{K(z) + \frac{1}{3}\underline G (z)}} \geqslant 0,\quad \forall z; \\ \delta {\mathbf{r}} \cdot {\mathbf{S}} \cdot \delta {\mathbf{r}} \geqslant {{\rho }_{\kappa }}({{l}_{3}})g{{(\delta {\mathbf{r}} \cdot {{{\mathbf{e}}}_{3}})}^{2}}. \\ \end{gathered} $

Второе неравенство в (3.17) означает, что упругая заделка на ${{\Sigma }_{ - }}$ должна иметь жесткость не меньше той, которая компенсирует “провисание” нижней части слоя. Если область $B$ не выходит на нижнюю граничную плоскость слоя (т.е. нулевые граничные условия ставятся на $\partial B{{\backslash }}{{\Sigma }_{ + }}$), то второго условия просто нет, а если считать, что имеется подстилающий слой, и на ${{\Sigma }_{ - }}$ имеется скачок плотности, то второе условие сводится к тому, что ${{\rho }_{\kappa }}({{l}_{3}} + 0)$ ≥ ${{\rho }_{\kappa }}({{l}_{3}} - 0)$ (отсутствие инверсии плотности). Будем считать, что второе неравенство в (3.17) выполнено.

Первое неравенство в (3.17) устанавливает диапазон значений $\frac{{d{{\rho }_{\kappa }}}}{{dz}}$, достаточных для устойчивости. Заметим, что это неравенство выполняется только при $\frac{{d{{\rho }_{\kappa }}}}{{dz}} > 0$ (хотя устойчивость может иметь место и при $\frac{{d{{\rho }_{\kappa }}}}{{dz}} < 0$). Преобразуем это неравенство к виду, позволяющему сопоставлять его с полученным необходимым условием (3.16):

(3.18)

$\frac{{d{{\rho }_{\kappa }}}}{{dz}} - \frac{{\rho _{\kappa }^{2}g}}{{K + \frac{1}{3}\underline G }}\, \geqslant \,0\, \Leftrightarrow \,\underline G \, \geqslant \,3\frac{K}{{\frac{{d{{\rho }_{\kappa }}}}{{dz}}}}\left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right),\;\forall z.$

Пусть

(3.19)

$\underline {\underline G } \equiv \mathop {\min }\limits_B \underline G ,\quad \bar {K} \equiv \mathop {\max }\limits_B K.$

Тогда более сильное неравенство (т.е. более грубое достаточное условие) принимает следующий вид:

(3.20)

$\underline {\underline G } \geqslant 3\frac{{\bar {K}}}{{\mathop {\min }\limits_B \left( {\frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right)}}\mathop {\max }\limits_B \left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right).$

4. ЗАКЛЮЧЕНИЕ

Заметим, что для объемно-упругих геоматериалов необходимое и достаточное условие устойчивости совпадают между собой [1–3] и равносильны следующему неравенству:

$\mathop {\max }\limits_B \left( {\frac{{\rho _{\kappa }^{2}g}}{K} - \frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right) \leqslant 0.$

Очевидно, что устойчивость объемно-упругого геомассива (который характеризуется нулевой сдвиговой жесткостью) влечет за собой заведомую устойчивость среды с ненулевой сдвиговой жесткостью. С точки зрения анализа устойчивости интерес представляет случай, когда соответствующая среда с нулевой сдвиговой жесткостью неустойчива (т.е. неравенство (4.1) нарушено), а при наличии сдвиговой жесткости устойчива (стабилизирующее влияние сдвиговой жесткости). Ответ на вопрос, при каких значениях сдвиговой жесткости это имеет место, дает как неравенство (3.18), так и более грубое достаточное условие (3.20), имеющее форму, удобную для сравнения с необходимым условием устойчивости (3.16).

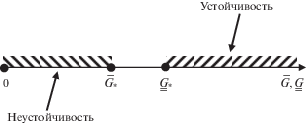
Учитывая тот факт, что сдвиговая жесткость геоматериала под влиянием тех или иных физических процессов может уменьшаться, очень важно выяснить, при каких конечных значениях сдвиговой жесткости система перестает быть устойчивой. Ответ на этот вопрос дает необходимое условие устойчивости (3.16), нарушение которого является достаточным условием неустойчивости. Заметим, что в (3.16) правая часть неравенства не зависит от распределения сдвиговых жесткостей в среде. Отсюда сразу же следует, что уменьшение сдвиговых жесткостей (влекущее за собой уменьшение $\bar {G}$) в итоге приведет к нарушению (3.16), что будет свидетельствовать об уже произошедшей потере устойчивости. Соотношение между диапазонами заведомой устойчивости и заведомой неустойчивости иллюстрирует рис. 2.

Рис. 2.

Диапазоны устойчивости и неустойчивости.

Подчеркнем следующее: несмотря на то что полученное необходимое условие устойчивости сильно отличается от полученного ранее достаточного условия, эти условия при стремлении всех сдвиговых жесткостей к нулю смыкаются друг с другом и в пределе сводятся к одному и тому же необходимому и достаточному условию устойчивости для объемно-упругого геомассива.

Список литературы

Рыжак Е.И., Мухамедиев Ш.А., Синюхина С.В. Условия и механизмы возникновения гравитационной неустойчивости слоистых объемно-упругих геомассивов // Физика Земли. 2016. № 6. С. 4–20. https://doi.org/10.7868/S0002333716060090
Мухамедиев Ш.А., Рыжак Е.И., Синюхина С.В. Об устойчивости двуслойной системы неоднородных тяжелых сжимаемых жидкостей // Прикладная математика и механика. 2016. Т. 80. Вып. 3. С. 375–385. https://elibrary.ru/item.asp?id=27175018
Ryzhak E.I., Mukhamediev Sh.A., Sinyukhina S.V. Conditions of Stability and Instability for a Pair of Arbitrarily Stratified Compressible Fluids in an Arbitrary Non-uniform Gravity Field // International Journal of Non-Linear Mechanics. 2017. V. 96C. P. 36–45. https://doi.org/10.1016/j.ijnonlinmec.2017.08.002
Рыжак Е.И., Синюхина С.В. Об устойчивости стратифицированных упругих геосистем в поле силы тяжести // ДАН. 2019. Т. 489. № 3. С. 298–302.
Knops R.J., Wilkes E.W. Theory of Elastic Stability // Handbuch der Physik. V.6a/3. Berlin: Springer–Verlag, 1973.
Hill R. On Uniqueness and Stability in the Theory of Finite Elastic Strain // J. Mech. Phys. Solids. 1957. V. 5. P. 229–241.
Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.
Truesdell C. A First Course in Rational Continuum Mechanics. Baltimore, Maryland: J. Hopkins Univ., 1972.
Truesdell C., Noll W. The Non-linear Field Theories of Mechanics // Handbuch der Physik V.III/3. Berlin: Springer–Verlag, 1965. 602 p.
Рыхлевский Я. О законе Гука // Прикладная математика и механика. 1984. Т. 48. Вып. 3. С. 420–435.
Gurtin M. The Linear Theory of Elasticity // Handbuch der Physik. V.6a/2. Berlin: Springer–Verlag, 1972. P. 1–295.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Науки о Земле

Архивы выпусков Информация о журнале Отправить рукопись в журнал