Доклады Российской академии наук. Науки о Земле, 2022, T. 504, № 1, стр. 91-96
Изменение характеристик внутренних колебаний океанической циркуляции в условиях глобального потепления
Член-корреспондент РАН А. Б. Полонский 1, *, А. Б. Федотов 1
1 Институт природно-технических систем
Севастополь, Россия
* E-mail: apolonsky5@mail.ru
Поступила в редакцию 20.09.2021
После доработки 26.11.2021
Принята к публикации 07.02.2022
- EDN: OJPYII
- DOI: 10.31857/S2686739722050127
Аннотация
На основании анализа серии численных экспериментов в рамках двухслойной океанической модели показано, что при ослаблении ветровой циркуляции в период глобального потепления должна наблюдаться трансформация спектра флюктуаций крупномасштабных течений. Основными проявлениями этой трансформации являются изменение интенсивности флюктуационных компонент в поле скорости течений и формирование значимых пиков в энергетических спектрах на типичных периодах около 25 лет. Этот эффект связан с усилением неустойчивости циркуляции и эволюцией крупномасштабных круговоротов.
ВВЕДЕНИЕ
Очевидно, что глобальное потепление, которое особенно интенсивно проявляется в высоких широтах Северного полушария, должно приводить к ослаблению океанической (в том числе, меридиональной) циркуляции. Наиболее выражено это ослабление должно проявляться в Северной Атлантике. Одна из главных причин такого ослабления заключается в снижении интенсивности конвекции в области формирования Североатлантической глубинной водной массы в условиях более теплого климата и сопутствующем ослаблении термохалинной циркуляции. Другая причина – ослабление ветровой циркуляции, возникающая вследствие уменьшения термического контраста между экватором и полюсом (также наиболее выраженного в Северной Атлантике), что приводит к ослаблению зональной циркуляции в атмосфере [1, 2]. В то же время существуют значительные расхождения между результатами численного моделирования долговременных циркуляционных тенденций в океане и экспериментальными оценками, основанными на обработке различных типов данных (например, массива RAPID-MOCHA, полученного в рамках международного проекта RAPID на 26°с.ш.). По крайней мере частично это расхождение может быть следствием недооценки большинством океанических и совместных моделей океана и атмосферы естественной междесятилетней изменчивости циркуляции [2–8].
Междесятилетняя изменчивость в климатической системе может генерироваться за счет неустойчивости ветровой океанической циркуляции в стратифицированном бассейне. Она представляет собой климатическую моду, обусловленную внутренними механизмами естественного происхождения, но может менять свои характеристики в процессе изменения основных параметров системы, в том числе вызванных вариациями внешнего ветрового воздействия [9].
В настоящей работе упрощенная двухслойная океаническая модель будет использована для моделирования крупномасштабной океанической циркуляции при стационарном внешнем воздействии различной интенсивности. Модели такого рода широко использовались в 1970–80-х годах для вихре-разрешающего моделирования циркуляции океана (например, [10, 11]). В последние годы аналогичные модели были применены для изучения различных динамических режимов в океане [12–14]. Эти результаты показывают, что упрощенные модели являются полезным инструментом для изучения общей циркуляции океана с явным разрешением мезомасштабных вихрей несмотря на некоторые очевидные ограничения. Основной целью настоящей работы является изучение изменения режима океанической циркуляции в условиях ослабления зональной циркуляции атмосферы и усиления вертикальной стратификации в связи с глобальным потеплением.
ЧИСЛЕННАЯ МОДЕЛЬ И МЕТОД ЕЕ ИНТЕГРИРОВАНИЯ
Модель эволюции потенциального вихря [15] для двухслойной жидкости на β-плоскости используется при заданной глубине верхнего (менее плотного) и нижнего слоев (H1 и H2 соответственно). Уравнения, описывающие динамику системы, выглядят следующим образом:
(1)
$\begin{gathered} \frac{{\partial {{\omega }_{j}}}}{{\partial t}} + \alpha J\left( {{{\psi }_{j}},{{\omega }_{j}}} \right) + \beta \frac{{\partial {{\psi }_{j}}}}{{\partial x}} = - {{\lambda }_{j}}{{\omega }_{j}}{{\delta }_{{j2}}} + {{W}_{j}}{{\delta }_{{j1}}} + {{D}_{j}}, \\ {{\omega }_{j}} = \Delta {{\psi }_{j}} + {{F}_{j}}\left( {{{\psi }_{i}} - {{\psi }_{j}}} \right);\quad j = 1,2;\quad i = 3 - j, \\ \end{gathered} $Индекс j = 1 соответствует верхнему слою, на который непосредственно воздействует ветер, а индекс j = 2 – нижнему слою, испытывающему сопротивление дна. Дополнительная диссипация в модели реализуется путем включения бигармонической вязкости в численную модель. Соотношение ${{F}_{1}}{\text{/}}{{F}_{2}}$ = ${{H}_{2}}{\text{/}}{{H}_{1}}$ определяет соотношение глубин нижнего и верхнего слоев, а абсолютные значения ${{F}_{1}}$ и ${{F}_{2}}$ определяют численное значение бароклинного радиуса деформации Россби – ${\text{Ro}}$ = = $2\pi {{\left( {{{F}_{1}} + {{F}_{2}}} \right)}^{{1/2}}}$.
Уравнения модели были преобразованы к безразмерному виду. Вычисления проводились в квадратной области со сторонами квадрата 2π. Ось X направлена на восток, оси Y – на север. Поток завихренности, поступающий в верхний слой за единицу времени, выражается как
где ${{W}_{0}}$ – амплитуда потока завихренности, обусловленного ветровым воздействием, которая в общем случае явно зависит от времени, но в данной постановке является заданной константой. Таким образом, южная половина расчетной области подвержена воздействию антициклонической завихренности, а северная половина – циклонической, что имитирует типичную климатическую ситуацию в Северной Атлантике. Поток завихренности ветра в нижний слой тождественно равен нулю. В модели заданы граничные условия непротекания и скольжения.Уравнения (1) решаются численно методом Аракавы [16] на девятиточечном шаблоне. Этот метод обладает свойством сохранения завихренности и интегралов второго порядка движения – кинетической энергии и энстрофии, что делает его удобным для решения задач гидродинамической неустойчивости и позволяет корректно изучать потоки энергии между слоями и по спектру. Аппроксимация адвекции – четвертого порядка точности по пространству. Производная по времени аппроксимируется методом “чехарда”. Система решается на каждом шаге методом прямого интегрирования путем разложения полей функции тока и относительной завихренности по собственным функциям дифференциального оператора задачи с учетом граничных условий для одной из пространственных координат и решения полученной системы линейных уравнений с трехдиагональной матрицей методом прогонки с последующим преобразованием переменных задачи в физические значения функции тока и относительной завихренности [17].
В численных экспериментах использовались по 513 узлов сетки вдоль каждой стороны квадрата и следующие безразмерные параметры: β = 1, коэффициенты бигармонического и придонного трения, равные соответственно 2.44 × 10–10 и 0.03, и шаг по времени 0.025. Контрольный эксперимент проводился при ${{F}_{1}}$ = 2900 и ${{F}_{2}}$ = 75 и с безразмерной амплитудой потока завихренности, генерируемого ветром, равной W0 = 0.001. В следующих 2-х численных экспериментах интенсивность ветрового воздействия увеличивалась путем задания W0 = = 0.00125 и W0 = 0.0015. Кроме этого проводился численный эксперимент с увеличением перепада плотности между слоями (приблизительно на 20%), имитирующим обострение стратификации в океане, и W0 = 0.001. Система интегрировалась до выхода на квазипериодический режим и далее еще как минимум на 550 лет модельного времени. Временные ряды полной и кинетической энергии в верхнем и нижнем слоях подвергались спектральному анализу. Использовалось прямое преобразование Фурье временных рядов за период после установления квазипериодического режима и до конца интегрирования с дальнейшим усреднением по трем частотам с весами 1–2–1 (т.е. использовался треугольный фильтр).
По аналогии с работами [12, 13] линейный размер области выбирался равным 3840 км, что примерно соответствует пространственным размерам крупномасштабных океанических круговоротов в Северной Атлантике и дает возможность использовать приближение β-плоскости [9]. При этом получались следующие масштабы перехода к размерным единицам: для 2πL = 3840 км имеем: L = 611 км (пространственный масштаб), U = βL2 = 7.09 м/с (масштаб скорости), T = (βL)–1 = = 86 400 с = 1 сут (временной масштаб), β = 1.9 × × 10–11 м–1 c–1. Бароклинный радиус деформации Россби в первых трех экспериментах был равен 70 км, а в последнем – 86 км.
РЕЗУЛЬТАТЫ
Выбранные параметры задачи обеспечивают реалистичные величины средней и максимальной скоростей течений в обоих слоях. В верхнем слое в первых трех численных экспериментах (при бароклинном радиусе деформации Россби, равном 70 км) средние скорости после выхода на квазипериодический режим составляют от 3.8 см/с (в эксперименте с ${{W}_{0}}$ = 0.001) до 4.3 см/с (при ${{W}_{0}}$ = 0.0015), а максимальные достигают соответственно 1.1 и 1.6 м/с. В нижнем слое скорости течений уменьшаются почти в два раза по сравнению с верхним. При обострении стратификации (и увеличении бароклинного радиуса деформации Россби до 86 км) в эксперименте с ${{W}_{0}}$ = 0.001 средние скорости в верхнем слое увеличиваются до 4.4 см/с, а максимальные – до 1.7 м/с. При этом в нижнем слое интенсивность циркуляции в целом уменьшается по сравнению со случаем менее стратифицированного океана. Другими словами, увеличивается сдвиг скорости по вертикали.
Рисунки 1, 2 и 3 демонстрируют, что при реалистических величинах скорости течений происходит формирование квазипериодического динамического режима, характеризующегося неустойчивостью крупномасштабной океанической циркуляции, формированием мезомасштабных вихрей, которые затем эволюционируют, самоорганизуются и отдают свою энергию среднему течению. Представление о пространственной структуре поля завихренности течений верхнего слоя при максимальной и минимальной кинетической энергии течений верхнего слоя дает рис. 3. Более подробно динамика мезомасштабных течений в двухслойном эксперименте, включая характер пространственных спектров по волновым числам, проанализирована в работах [13, 14].
Рис. 1.
Временной ход (слева) и спектр кинетической энергии течений верхнего слоя (справа) в безразмерных единицах при W0 = 0.001 (черные кривые) и W0 = 0.0015 (красные кривые). Бароклинный радиус деформации Россби равен 70 км.
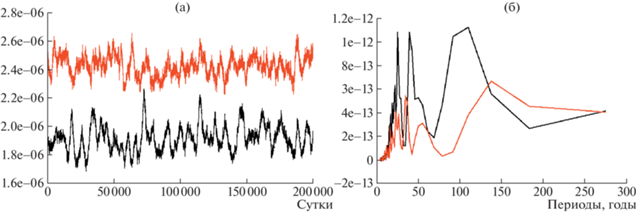
Рис. 2.
Временной ход (слева) и спектр кинетической энергии течений верхнего слоя (справа) в безразмерных единицах при W0 = 0.001. Бароклинный радиус деформации Россби равен 70 км (черные кривые) и 86 км (красные кривые).

Рис. 3.
Поле завихренности течений верхнего слоя при минимальной и максимальной величинах кинетической энергии течений в контрольном эксперименте, W0 = 0.001 (слева и справа соответственно). Временной ход кинетической энергии течений верхнего слоя океана приведен на рис. 1.

Наиболее интересный результат проведенных численных экспериментов заключается в том, что при усилении ветрового воздействия и интенсификации океанической циркуляции происходит очень существенная трансформация частотного спектра флюктуаций кинетической энергии (и, соответственно, скорости) течений. При величине бароклинного радиуса деформации Россби, равном 70 км, и максимальной амплитуде ветрового воздействия вклад флуктуаций с периодами около 35 лет в общую кинетическую энергию возрастает, а более высокочастотных и более низкочастотных вариаций – уменьшается. Если в эксперименте с минимальной интенсивностью ветрового воздействия вариации кинетической энергии с типичным периодом около 25 и 40 лет значимы на 80% уровне, то при максимальной интенсивности ветра и неизменной величине бароклинного радиуса деформации Россби значимые пики в спектре на этих периодах пропадают. Одновременно при усилении ветрового воздействия увеличивается относительная амплитуда колебаний с типичными периодами 35 лет, а пик в более низкочастотной части спектра смещается в область периодов, близких к 150 годам. При этом значимость пика на периодах около 35 лет достаточно высока (на уровне 80%-го доверительного интервала), а пик на более низких частотах статистически незначим.
Отметим, что при увеличении кинетической энергии средних течений суммарная энергия квазипериодических мод уменьшается. Так, например, дисперсия кинетической энергии флюктуаций поля течений верхнего слоя океана в эксперименте с ${{W}_{0}}$ = 0.001 превышает аналогичную дисперсию в эксперименте с ${{W}_{0}}$ = 0.0015 в 1.65 раза. Причем уменьшение интенсивности флюктуаций вектора течений особенно выражено в высокочастотной и низкочастотной областях спектра – вблизи наиболее энергонесущих частот (рис. 1).
Эксперимент с повышенным вертикальным перепадом плотности между слоями свидетельствует о том, что обострение стратификации (наряду с ослаблением интенсивности ветровой циркуляции) также способствует увеличению амплитуды квазипериодических вариаций поля течений верхнего слоя океана в относительно высокочастотной части спектра. Особенно выражена интенсификация высокочастотных компонент с периодами около 25 лет (рис. 2). Уровень статистической значимости спектрального пика на соответствующих периодах повышается до 90%. По-видимому, это является прямым следствием увеличения доступной потенциальной энергии, интенсификации течений в верхнем слое стратифицированного океана, увеличения вертикального сдвига скорости при потеплении и большей бароклинной неустойчивости крупномасштабных течений [9]. При этом пик в более низкочастотной части спектра (в области характерных периодов ~100 лет) пропадает.
Таким образом, при ослаблении ветровой циркуляции в период глобального потепления следует ожидать увеличение энергии флюктуаций поля течений в относительно высокочастотной области спектра и формирование в этой области пиков с большим уровнем значимости. В Северной Атлантике периоды, к которым приурочены эти пики, составляют первые десятки лет. Это не такое очевидное следствие глобального потепления, как меридиональное смещение субтропических круговоротов к северу, вызванных происходящим смещением шторм-треков к северу, или возможная термохалинная катастрофа, связанная с коллапсом меридиональной термохалинной циркуляции [1, 2]. Оно связано с изменением интенсивности ветрового воздействия и стратификации, большей неустойчивостью системы крупномасштабных течений при потеплении и сопутствующей трансформацией эволюции крупномасштабных океанических круговоротов во времени.
Более или менее детальное обсуждение применимости результатов моделирования в рамках упрощенной двухслойной модели к реальному океаническому бассейну в рамках настоящей работы не представляется возможным из-за ограниченности объема статьи. Тем не менее можно отметить два следующих обстоятельства. Классические работы, посвященные анализу общей циркуляции вод Мирового океана и описанию особенностей динамики крупномасштабных океанических круговоротов, основывались на еще более простых моделях, допускающих аналитические решения [18, 19]. Полученные в настоящей работе значимые флуктуации поля течений на десятилетних временных масштабах близки по типичным периодам к соответствующим флюктуациям, наблюдаемым в Северной Атлантике [20].
ЗАКЛЮЧЕНИЕ
Краткий анализ проведенных численных экспериментов показал, что при ослаблении ветровой циркуляции в период глобального потепления следует ожидать формирование в спектрах кинетической энергии области с повышенной флуктуационной энергией океанической циркуляции на десятилетних временных масштабах. Последнее связано с неустойчивостью океанической циркуляции и эволюцией крупномасштабных круговоротов. Соответствующие этим частотам периоды для Северной Атлантики составляют порядка 25 лет.
Список литературы
IPCC: Climate Change. Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change / [Core Writing Team, R.K. Pachauri and L.A. Meyer (eds.)]. IPCC. Geneva, Switzerland. 2014. 151 p.
Polonsky A. The Ocean’s Role in Climate Change. / Cambridge Scholars Publishing. Newcastle upon Tyne, UK. 2019. 276 p.
Roberts C.D., Jackson L., McNeall D. Is the 2004–2012 Reduction of the Atlantic Meridional Overturning Circulation Significant? // Geophys. Res. Lett. 2014. V. 41. P. 3204–3210. https://doi.org/10.1002/2014GL059473
Schmith T., Yang S., Gleeson E., Semmler T. How Much Have Variations in the Meridional Overturning Circulation Contributed to Sea Surface Temperature Trends since 1850? A Study with the EC-Earth Global Climate Model. // J. Clim. 2014. V. 27. P. 6343–6357. https://doi.org/10.1175/JCLI-D-13-00651.1
Danabasoglu G., Yeager S.G., Kim W.M., et al. North Atlantic Simulations in Coordinated Ocean-ice Reference Experiments Phase II (CORE-II). Part II: Inter-annual to Decadal Variability // Ocean Model. 2016. V. 97. P. 65–90. https://doi.org/10.1016/j.ocemod.2015.11.007
Reintges A., Martin T., Latif M., Keenlyside N.S. Uncertainty in Twenty-first Century Projections of the Atlantic Meridional Overturning Circulation in CMIP3 and CMIP5 Models // Clim. Dyn. 2017. V. 49. P. 1495–1511. https://doi.org/10.1007/s00382-016-3180-x
Smeed D.A., Josey S.A., Beaulieu C., et al. The North Atlantic Ocean Is in a State of Reduced Overturning. // Geophys. Res. Lett. 2018. V. 45. P. 1527–1533. https://doi.org/10.1002/2017GL076350
Yan X., Zhang R., Knutson T.R. Underestimated AMOC Variability and Implications for AMV and Predictability in CMIP Models. // Geophys. Res. Lett. 2018. V. 45. P. 4319–4328. https://doi.org/10.1029/2018GL077378
Pedlosky J. Geophysical Fluid Dynamics. / Springer Verla, New York. 1987. 710 p.
Cane M.A. The Response of an Equatorial Ocean to Simple Wind Stress Patterns. Parts 1–2. // J. Marine Res. 1979. V. 37. P. 233–299.
Holland W.R. Quasi-geostrophic Modelling of Eddy-Resolved Ocean Circulation. In: O’Brien J.J. (eds.) / Advanced Physical Oceanographic Numerical Modelling. NATO ASI Series (Series C: Mathematical and Physical Sciences). 1986. V. 186. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-0627-8_14
Shevchenko I., Berloff P. On the Role of Baroclinic Modes in Eddy-resolving Midlatitude Ocean Dynamics // Ocean Modelling. 2017. V. 111. P. 55–65.
Федотов А.Б. Анализ временных масштабов долгопериодной изменчивости ветровой океанической циркуляции в двухслойном океане // Системы контроля окружающей среды. 2017. № 10 (30). С. 96–101.
Федотов А.Б. Долгопериодная изменчивость системы крупномасштабной циркуляции океана и мезомасштабных вихрей как явление самоорганизации // Океанологические исследования. 2019. Т. 47. № 3. С. 206–219.https://doi.org/10.29006/1564-2291.JOR-2019.47(3).16
Rhines P.B. Geostrophic Turbulence // Ann. Rev. Fluid Mech. 1979. V. 11. P. 401–441.
Arakawa A. Computational Design of Long-term Numerical Integration of the Equations of Fluid Motion, Two-dimensional Incompressible Flow // Journal of Comput. Physics. 1966. V. 1. № 1. P. 119–143.
Roache P.J. Computational Fluid Dynamics / Hermosa Publishers Albuquerque, N.M. 1972. 446 p.
Stommel H. The Westward Intensification of Wind Driven Ocean Currents // Eos Trans. Amer. Geophys. Union. 1948. V. 29. P. 202–206.
Munk W.H. On the Wind-Driven Ocean Circulation. // Journal of Meteorology. 1950. V. 7. № 2. P. 80–93. https://doi.org/10.1175/1520-0469(1950)007< 0080:OTWDOC.2.0.CO;2
Parsons L.A., Loope G.R., Overpeck J.T., et al. Temperature and Precipitation Variance in CMIP5 Simulations and Paleoclimate Records of the Last Millennium // J. of Climate. 2017. V. 30. № 22. P. 8885–8912. https://doi.org/10.1175/JCLI-D-16-0863.1
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Науки о Земле


