Доклады Российской академии наук. Науки о Земле, 2022, T. 507, № 2, стр. 316-322

Хорошо известно, что звуковые волны способны распространяться в глубоком океане на сотни и даже тысячи километров благодаря существованию подводного звукового канала (ПЗК). Эффект дальнего распространения звука представляет несомненный интерес с точки зрения практических приложений, таких как гидроакустическая томография [1–3], звукоподводная связь [4, 5] и подводная навигация [6]. Однако исследования последних тридцати лет показали, что звуковые сигналы могут испытывать сильную декогеренцию, связанную с лучевым хаосом [7]. Лучевой хаос означает крайне нерегулярную форму лучевых траекторий, обусловленную их неустойчивостью по Ляпунову. Основной причиной возникновения лучевого хаоса при дальнем распространении звука является накопительный эффект от рассеяния на малых неоднородностях поля скорости звука, вызванных океаническими внутренними волнами. Проявления лучевого хаоса в интерференционной структуре волнового поля получили название волнового хаоса [7–10].

Важно понимать, что дальнее распространение звука описывается линейными волновыми уравнениями. Решения таких уравнений не могут быть неустойчивыми по Ляпунову, т.е. обладать неустойчивостью по отношению к малым вариациям начальных условий. Однако, как было показано в работе [11], распространение волн в волноводе с хаотической динамикой лучей обладает острой чувствительностью не к вариациям начальных условий, а вариациям самой среды. Данное обстоятельство не только затрудняет моделирование акустических полей, поскольку океаническая среда практически всегда известна только приближенно, но и накладывает существенные ограничения на возможности звукоподводной связи. Это особенно ярко проявляется при реализации одной из наиболее перспективных схем звукоподводной связи, основанной на обращении волнового фронта [12–14]. Эта схема основана на использовании пробного источника и приемно-передающей антенной решетки, выполняющей роль акустического зеркала. Сигнал от пробного источника принимается антенной решеткой и переизлучается обратно после обращения фаз. В случае стационарной среды выполняется принцип взаимности, согласно которому переизлученное поле должно фокусироваться в области пробного источника, обеспечивая повышенное значение соотношения сигнал/шум [3]. Однако даже малые различия океанической среды, имеющие место при распространении звукового сигнала до акустического зеркала и обратно, способны нарушить принцип взаимности. При дальнем распространении звука эти нарушения должны быть особенно значительными, как вследствие большого времени распространения, так и вследствие лучевого хаоса [14].

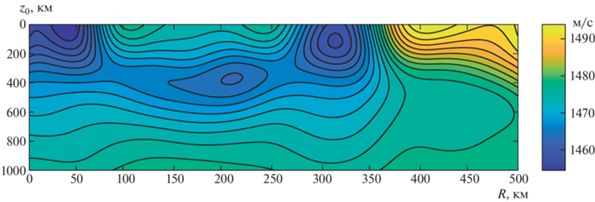
В настоящей работе мы намерены исследовать процесс рефокусировки акустического поля посредством обращения волнового фронта для реалистичной модели океана, включающей в себя существенные крупномасштабные неоднородности. В частности, мы рассмотрим модель ПЗК, построенного на основе натурных гидрологических данных, полученных в рейсе японского научно-исследовательского судна “Кофу Мару” в апреле 2004 г. [15]. Трасса ПЗК начинается от острова Хоккайдо и ориентирована на юго-восток. Она характеризуется довольно значительными изменениями фонового профиля скорости звука, в том числе обусловленными синоптическими вихрями (см. рис. 1).

Само по себе нарушение принципа взаимности при дальнем распространении звука имеет глубокие корни и тесно связано с возникновением необратимости в неинтегрируемых квантовых системах. Рефокусировка акустического поля в окрестности пробного источника представляет собой пример так называемого “эха Лошмидта”, ставшего в свое время предметом очень активного исследования в контексте проблемы квантового хаоса [16]. В качестве меры “эха Лошмидта” традиционно используется воспроизводимость, которая в терминах акустики океана может быть определена следующим образом [17]:

где ${{\Psi }_{{{\text{pr}}}}}(z)$ и ${{\Psi }_{{{\text{rev}}}}}(z)$ – вертикальные профили пробного и рефокусированного акустических полей соответственно. Анализ, проведенный авторами, свидетельствует о том, что в режиме развитого хаоса воспроизводимость спадает с ростом расстояния по супер-гауссову закону, с показателем экспоненты около 2.4–2.5 для частот от 75 до 150 Гц. Появление синоптических вихрей может как существенно усилить, так и существенно ослабить рассеяние звука на внутренних волнах [2], что проявляется в характере спадания воспроизводимости.

Для моделирования акустических полей использован новый подход, основан на вычислении пропагатора акустического поля $\hat {G}\left( {r{\kern 1pt} '',r{\kern 1pt} '} \right)$, определяемого как [18, 19]

где $\Psi (r,z)$ – вертикальный профиль огибающей акустического поля на расстоянии r в горизонтальной плоскости от источника. Связь $\Psi (r,z)$ с акустическим давлением P устанавливается формулой где f – частота звука, ${{c}_{0}}$ – референтное значение скорости звука.

Используя базис нормальных мод волновода, являющихся решениями задачи Штурма–Лиувилля

где $n = {{c}_{0}}{\text{/}}c(r,z)$ – показатель преломления звуковых волн, можно представить акустическое поле как сумму

Применив разложение поля по модам (6), мы можем представить пропагатор в виде матрицы с элементами

Уравнение (2) в матричном представлении принимает вид

где $\vec {a} = {{({{a}_{1}},{{a}_{2}}, \ldots ,{{a}_{M}})}^{T}}$ – вектор модовых амплитуд, M – общее число захваченных в подводный звуковой канал мод.

Подход, предложенный в [18, 19], основан на разделении волновода на сегменты и представлении пропагатора в виде произведения случайных матриц

где ${{{\mathbf{G}}}_{k}}(\Delta {{r}_{k}})$ – пропагатор k-го волноводного сегмента длиной $\Delta {{r}_{n}}$, а матрица ${{{\mathbf{S}}}_{k}}$ описывает преобразование модового базиса между соседними сегментами,

В качестве мод “нулевого сегмента” (k = 0) выступают моды, используемые для разложения поля источника (например, локальные моды в области источника). Полагая, что размер сегмента является достаточно малым, мы можем воспользоваться теорией возмущения:

где ${\mathbf{I}}$ – единичная матрица, ${\mathbf{D}}$ – диагональная матрица с элементами, определяемыми по формуле а ${{\delta }_{{mn}}}$ – символ Кронекера, а ${\mathbf{A}}$ – матрица возмущения.

Чтобы определить последнюю, положим, что вариации скорости звука описываются моделью, предложенной в [20]:

где ${{j}_{{\max }}} = 50$, $\xi (z) = {{e}^{{ - z{\text{/}}B}}} - {{e}^{{ - h{\text{/}}B}}}$, $B = 500$ м – глубина термоклина, ${{j}_{*}} = 3$. Горизонтальные вариации скорости звука определяются функциями где ${{\phi }_{{ij}}}$ – случайные фазы, а амплитуды описываются выражением, соответствующим спектру Гарретта-Манка: ${{k}_{j}} = \pi j{{f}_{{\text{i}}}}{\text{/}}({{N}_{0}}B)$, ${{N}_{0}} = 2\pi {\text{/}}10$ м^–1, ${{f}_{i}}$ – инерционная частота, равная 1 циклу в сутки. Амплитудный множитель ${{V}_{0}}$ определяется выражением где g – ускорение свободного падения, ${{E}_{{{\text{iw}}}}}$ – безразмерный параметр, характеризующий энергию внутренних волн. Описанная выше модель соответствует матрице возмущения с элементами следующего вида: где

Величины $Z_{{mn,j}}^{{(\alpha )}}$ представляют собой матричные элементы вертикальных мод поля внутренних волн,

Выражение (18) включает в себя гауссовы случайные величины ${{y}_{{j,\alpha ,n}}}$, статистические свойства которых описываются следующими выражениями:

где ${{k}_{\alpha }} = 2\pi {\text{/}}\Delta {{r}_{\alpha }}$. Изменчивость среды во времени учитывается в фазовом сдвиге ${{\beta }_{{j,\alpha ,n}}}$ между звуковыми волнами, распространяющимися в направлении от акустического зеркала и к нему. Он равен нулю для пропагатора, отвечающего распространению в направлении зеркала, а для обратного направления может быть приближенно оценен по формуле где ${{\omega }_{{jn}}}$ – частота внутренней волны, которую мы можем найти как

Таким образом, мы можем учесть изменчивость среды в процессе прохождения сигнала в прямом и обратном направлениях. Теперь перейдем к вопросу о влиянии этой изменчивости на эффективность рефокусировки акустического поля. Для удобства последующего анализа введем нормированную интенсивность акустического поля, переизлученного в область пробного источника,

Тогда ширина переизлученного волнового пакета может быть оценена как

где а угловые скобки означают усреднение по реализациям поля внутренних волн.

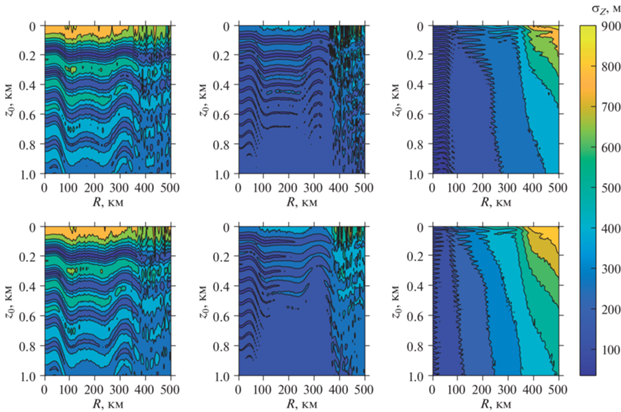
На рис. 2 с помощью цветовой модуляции представлена зависимость ширины переизлученного пакета от глубины пробного источника ${{z}_{0}}$ и расстояния между пробным источником и акустическим зеркалом R. Все вычисления сделаны для случая точечного пробного источника. Рассматриваются звуковые частоты 25, 50 и 100 Гц. Для всех трех частот и R < 350 км зависимость ширины волнового пакета сильно осциллирует с изменением глубины пробного источника. Эти осцилляции связаны с положением интерференционных пиков волноводных мод. При R > 350 км начинает сказываться волновой хаос, и они становятся размытыми, а в случае 100 Гц – и вовсе исчезают. Вместо осцилляций возникает тенденция роста ширины волнового пакета по мере приближения к поверхности океана. При этом ее значения становятся порядка нескольких сотен метров, т.е. рефокусировка не наблюдается. Происходит свойственное волновому хаосу диффузионное расплывание акустического поля, проявляющееся в одновременном увеличении и интервала глубин, занимаемых волновым пакетом, и ширины углового спектра акустического поля [8].

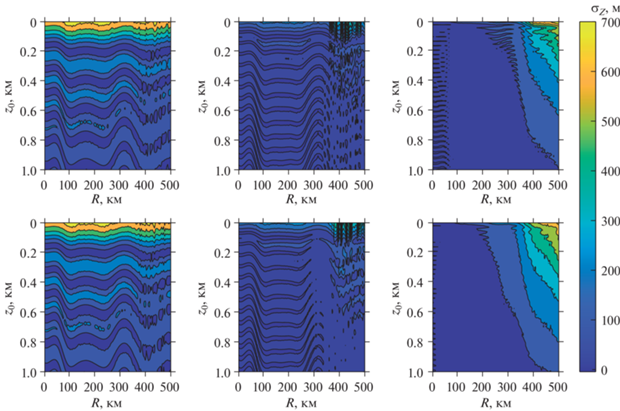
Картину хаотического расплывания подтверждают данные, представленные на рис. 3, где изображена аналогичная зависимость смещения центра переизлученного волнового пакета относительно глубины источника, $\delta z = \left\langle z \right\rangle - {{z}_{0}}$. Мы видим, что с увеличением дистанции происходит смена осциллирующей зависимости δz от глубины на почти монотонный рост с уменьшением глубины пробного источника. Это означает, что при наличии существенного вклада волнового хаоса фазовое сопряжение перестает обеспечивать эффективную засветку области пробного источника и, как следствие, соотношение сигнал/шум значительно уменьшается. Последнее обстоятельство означает существенное ухудшение условий для реализации звукоподводной связи. Отметим, что пятикратное увеличение энергии внутренних волн мало оказывает лишь незначительное влияние на структуру диаграмм, приведенных на рис. 2 и 3. Отсюда можно сделать предположение, что ключевым фактором необратимости волновой эволюции является изменчивость фонового профиля скорости звука, обусловленная синоптическими вихрями. В частности, мы наблюдаем резкий рост хаотичности сразу после прохождения холодного вихря с ядром на глубине около 100 м. Влияние синоптических вихрей на степень хаотичности распространения звуковых волн ранее рассматривалось в работах [2, 19].

Теперь попробуем найти оптимальное положение пробного источника с точки зрения рефокусировки акустического поля. Степень рефокусировки может быть оценена как величина обратного числа главных компонент IPR (inverse participation ratio), определяемого как

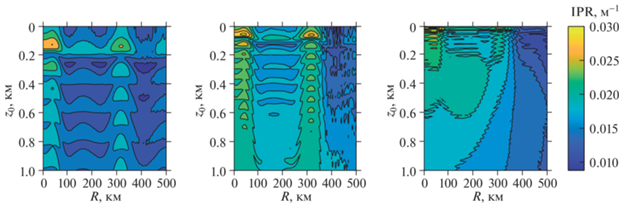
Зависимость IPR от глубины пробного источника и расстояния между источником и приемником показана на рис. 4. Мы видим две зоны наиболее сильной рефокусировки. Первая из них предсказуемо расположена на расстоянии порядка длины цикла луча от акустического зеркала. А вот наличие второй из них является несколько неожиданным – она расположена на расстоянии около 300 км от зеркала, когда влияние рассеяния на внутренних волнах уже является достаточно сильным. Отметим, что ее положение не зависит от частоты сигнала. Отсюда можно сделать вывод, что положение данной зоны не определяется особенностями интерференции мод акустического поля. Сопоставляя рис. 4 с другими рисунками, можно сделать предположение, что наличие еще одной зоны эффективной рефокусировки связано с формой опорного профиля скорости звука: эта зона возникает тогда, когда опорный профиль скорости звука в точке расположения пробного источника наиболее близок по форме к профилю в точке расположения акустического зеркала (см. рис. 1).

В заключение отметим основные результаты данной работы. Показано, что изменчивость океанической среды во времени, обусловленная полем внутренних волн, способна существенно ограничивать возможности рефокусировки акустического поля посредством обращения волнового фронта. Для рассмотренной в данной работе волноводной трассы рефокусировка становится практически невозможной для расстояний, превышающих 350 км. В значительной степени это ограничение связано с крупномасштабной изменчивостью фонового профиля скорости звука, обусловленной присутствием синоптических океанических вихрей вдоль трассы. С другой стороны, нами выявлена зона повышенной рефокусировки на расстоянии около 300 км от антенной решетки, выполняющей роль акустического зеркала. Мы предполагаем, что появление этой зоны связано с похожестью профилей скорости звука в точках пробного источника и акустического зеркала. Поскольку данный результат имеет практическое значение с точки зрения звукоподводной связи, планируется проверка данной гипотезы в дальнейших работах.