Доклады Российской академии наук. Науки о Земле, 2023, T. 508, № 2, стр. 290-296

Интенсивная деятельность человека по освоению природных ресурсов Мирового океана включает разведку, добычу и транспортировку полезных ископаемых, одними из последствий которых являются возникновение и распространение загрязнений различного характера. Так, количество утечек нефти колеблется от 5 до 17% от объема производства, при этом теряется не только ценное сырье, но и наносится значительный ущерб окружающей среде. Экспериментальному и теоретическому изучению растекания нефти и нефтепродуктов (далее для краткости называемыми олеинами) посвящена обширная научная литература, как физико-техническая [1–4], посвященная проблеме описания динамики самого процесса, так и экологическая [5], направленная на решение возникающих проблем очистки морских районов, направлений. В условиях Арктики возникает дополнительная проблема, связанная с распространением олеинов над и под ледяным покровом Северного Ледовитого океана, а также на заснеженной поверхности [6, 7].

В данной работе предложена упрощенная математическая модель, позволяющая исследовать основные динамические параметры процесса растекания. В этой модели химический состав и все термодинамические параметры среды считаются постоянными величинами, масса растекающегося пятна предполагается неизменной, все среды однородны и изотропны. Представлено сравнение с результатами лабораторных экспериментов по динамике разлива моторного масла и сырой нефти.

Растекание олеинов сопровождается рядом механических и термодинамических процессов. Поэтому при создании модели распространения необходимо учитывать следующие основные факторы, влияющие на динамику разлива: переход потенциальной энергии системы олеин–вода в кинетическую энергию из-за изменения геометрических характеристик разлива с течением времени; вязкое вовлечение воды в движение из-за касательных напряжений на границе олеин–вода, сопровождающееся замедление горизонтального движения олеина; возникновение течения в воде, вызванного вертикальным смещением нижней границы разлива олеина; возникновение движения воды из-за явления сопротивления формы разлива олеина, сопровождающегося его движением в воде; изменение количества поверхностной энергии системы “олеин в воде” по причине изменения площадей контактных границ “олеин–вода”, “олеин–воздух”, “воздух–вода”; вязкие тепловые потери в олеине и воде.

Приближенная модель основана на форме олеинового пятна в виде диска, радиус $R(t)$ и толщина $h(t)$ которого считаются функциями времени. Потенциальная и кинетическая энергии воздуха, вовлекаемого в движение разливом нефтепродуктов, не принимаются во внимание. Движение воды во время разлива олеина вызвано тремя основными механизмами – вязким захватом воды потоком олеина на границе их контакта, генерацией потенциального потока воды из-за смещения вверх нижней границы оленового пятна и производством потока воды из-за явления сопротивления формы растекания олеина в воде. В рассматриваемой упрощенной модели глубина воды считается бесконечной, а ее свободная поверхность – плоской и расположенной на уровне $z = 0$ цилиндрической системы координат, вертикальная ось $z$ которой направлена против вектора силы тяжести и проходит через центр олеинового пятна.

Потенциальная энергия исследуемой механической системы задается величиной

где ${{M}_{o}}$ – постоянная масса олеина, $\rho = {{{{\rho }_{o}}} \mathord{\left/ {\vphantom {{{{\rho }_{o}}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}$ – отношение плотностей олеина и воды.

Кинетическая энергия описывается выражением

где ${\mathbf{v}}$, ${\mathbf{w}}$ – поля скорости в олеине и воде соответственно; ${{h}_{ \pm }}(t)$ – вертикальные координаты верхней и нижней границ олеинового пятна, так что $h(t) = {{h}_{ + }}(t) - {{h}_{ - }}(t)$; $r$, $z$ – радиальная и вертикальная координаты.

Поверхностная энергия системы задается величиной

где ${{\lambda }_{S}} = \sqrt {{{\left| {{{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}} \right|} {{{\rho }_{o}}g}}} \right. \kern-0em} {{{\rho }_{o}}g}}} $ – капиллярная постоянная контактной линии “олеин–вода–воздух”, ${{\sigma }_{{ij}}}$ – коэффициент поверхностного натяжения на границе раздела $i$-й и $j$-й сред. Скорость вязкой диссипации определяется соотношением где ${{\Sigma }_{{\text{u}}}} = 2{{({{\partial {{{\text{u}}}_{r}}} \mathord{\left/ {\vphantom {{\partial {{{\text{u}}}_{r}}} {\partial r}}} \right. \kern-0em} {\partial r}})}^{2}}$ + ${{({{\partial {{{\text{u}}}_{r}}} \mathord{\left/ {\vphantom {{\partial {{{\text{u}}}_{r}}} {\partial z}}} \right. \kern-0em} {\partial z}} + {{\partial {{{\text{u}}}_{z}}} \mathord{\left/ {\vphantom {{\partial {{{\text{u}}}_{z}}} {\partial r}}} \right. \kern-0em} {\partial r}})}^{2}}$ + + $2{{({{\partial {{{\text{u}}}_{z}}} \mathord{\left/ {\vphantom {{\partial {{{\text{u}}}_{z}}} {\partial z}}} \right. \kern-0em} {\partial z}})}^{2}}$; ${\mathbf{u}} = {\mathbf{v}}$ в олеине, ${\mathbf{u}} = {\mathbf{w}}$ в воде.

Уравнение динамики энергии системы имеет вид

Для того чтобы система уравнений (1–5) приводила к конструктивным результатам, необходимо задаться моделью полей скорости в олеине и в воде. Так, как обе жидкие среды считаются несжимаемыми

то с учетом кинематических и динамических граничных условий а также того факта, что поля скорости удовлетворяют уравнению Навье–Стокса для каждой среды, в данной приближенной модели имеют место соотношения для олеина и для воды при $r \leqslant R(t)$где введены обозначения

Здесь ${{\nu }_{o}}$, ${{\nu }_{w}}$ кинематические, и ${{\eta }_{o}}$, ${{\eta }_{w}}$ динамические вязкости олеина и воды; ${{\kappa }_{{ij}}}$ – коэффициент вязкого вовлечения $i$-й жидкости в движение $j$-й жидкостью; ${{\Phi }_{w}}$ – потенциал поля скорости в воде, обусловленный вертикальным смещением нижней границы олеина. Подстановка (9–11) в выражения (1–4), выполнение необходимых расчетов с учетом того, что в реальных условиях $h\,\, \ll \,\,R$, $\sqrt {{{\nu }_{w}}t} \, \ll \,\,R$ и $\sqrt {{{\nu }_{o}}t} \, \ll \,\,R$ (даже для самых вязких сортов нефти) во все моменты времени наблюдения за процессом, и принимая во внимание малость величины $\left| {\frac{{\dot {h}}}{{\dot {R}}}} \right|$ = $\left| {\frac{1}{{\dot {R}}}\left( {\frac{{\dot {V}}}{{\pi {{R}^{2}}}}} \right)} \right|$ = $\frac{{2V}}{{\pi {{R}^{3}}}} \ll 1$, где $V$ – объем разлитого олеина, позволяет преобразовать уравнение динамики энергии системы (5) к виду

где введена переменная $F = {{\pi }^{2}}{{R}^{4}}$ – квадрат площади разлива нефти, и использованы обозначения

Численный анализ экспериментальных данных с минеральным маслом Volga M8B-SAE 20 API показывает, что значение ${{3{{{\dot {F}}}^{2}}} \mathord{\left/ {\vphantom {{3{{{\dot {F}}}^{2}}} {4F}}} \right. \kern-0em} {4F}}$ значительно меньше значения $\ddot {F}$, и им можно пренебречь. В то же время выражение для коэффициента ${{d}^{2}}$ в (13) указывает на значительный вклад вязких потерь только в начальные моменты времени разлива, когда вязкие напряжения в среде имеют существенные значения. Это позволяет не учитывать последний член уравнения (12). В результате таких приближений уравнение динамики энергии принимает вид

более того, коэффициенты этого уравнения рассматриваются как постоянные значения, несмотря на наличие в них зависящего от времени значения $\alpha $. Это обусловлено тем, что скорость изменения $\alpha $ значительно меньше скорости изменения радиуса растекания $R$:

Решение уравнения (14) делится на два варианта. В первом случае разлив олеина ограничен по площади, когда на поверхности воды может образоваться олеиновая линза, как конечное равновесное состояние системы. Этому случаю соответствует $\operatorname{sign} (\sigma )$ = 1. В целях дальнейшего описания вводится обозначение $\mu = \sqrt {\left| {{{b}^{2}} - {{a}^{4}}} \right|} $. Если ${{a}^{4}} < \,\,{{b}^{2}}$, то решение (14) имеет вид

где ${{F}_{*}} = \mathop {\lim }\limits_{t \to \infty } F(t) = {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}} = {{(1 - \rho ){{V}^{2}}} \mathord{\left/ {\vphantom {{(1 - \rho ){{V}^{2}}} {2\lambda _{s}^{2}}}} \right. \kern-0em} {2\lambda _{s}^{2}}}$, а ${{F}_{0}} = {{\left. F \right|}_{{t = 0}}}$, ${{F}_{1}} = {{\left. {\dot {F}} \right|}_{{t = 0}}}$ – величины, определяемые начальными условиями.

Как видно из (15), площадь разлива $S = {{F}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ проявляет колебательное и затухающее поведении во времени. Частота колебаний вблизи положения равновесия определяется величиной $2\pi \,b$, а коэффициент затухания колебаний во времени определяется величиной ${{a}^{2}}$. В случае существенного значения коэффициента затухания, когда ${{a}^{4}} > \,\,{{b}^{2}}$, решение (14) имеет вид

Во втором случае происходит разлив олеина с неограниченной площадью, когда нет предельного состояния равновесия системы, что соответствует значению ${\text{sign}}(\sigma ) = - 1$. Для описания результатов вводятся обозначения

и решение (14) имеет вид (16), в который подставляются значения (17). Решение для значений (17) включает в себя два экспоненциальных члена, один из которых пропорционален $\exp \left( { - \left( {{{a}^{2}} + \sqrt {{{a}^{4}} + {{b}^{2}}} } \right)t} \right)$, а другой – значению $\exp \left( {\left( {\sqrt {{{a}^{4}} + {{b}^{2}}} - {{a}^{2}}} \right)t} \right)$. Первый член быстро затухает во времени, а второй неограниченно растет, что обусловлено некомпенсированной силой поверхностного натяжения, действующей на границе контакта трех сред и направленной радиально от края олеинового пятна во внешнюю область.

Лабораторные эксперименты проводились с различными типами органических и минеральных масел и непосредственно с сырой нефтью. В качестве базовой жидкости использовалась вода разной температуры, как пресная, так и с разными соленостями. Исследование динамики распространения олеина по поверхности воды проводилось в прямоугольной кювете длиной 50 см, шириной 40 см и глубиной 5 см. Чтобы избежать бликов от поверхности воды и пятен углеводородов, поверхность жидкости освещалась сверху тремя разнесенными источниками света, расположенными рядом с кюветой по бокам.

Экспериментальный метод включал нанесение различных количеств моторного масла Volga M8B-SAE 20 API (${{{{\rho }}}_{{\text{o}}}} = 883.7$ км/м³, ${{{{\nu }}}_{o}} = 3.34 \times {{10}^{{ - 4}}}$ м²/с, при температуре $T$ = 20°C) и сырой нефти Мамонтовского месторождения (${{{{\rho }}}_{{\text{o}}}} = 878.0$ км/м³, ${{{{\nu }}}_{o}} = 2.15 \times {{10}^{{ - 5}}}$ м²/с, при температуре $T$ = 20°C) на поверхность известного объема воды и дальнейший мониторинг ее распространения по поверхности жидкости. Ход экспериментов записывался с помощью цифровой камеры в автоматическом режиме в течение 4 ч, съемка велась с частотой 360 кадров в минуту, а полученные последовательности кадров обрабатывались и анализировались. Положение масляного пятна регистрировали с использованием метода фотометрии обработанных изображений, полученных из исходных кадров методами пакетной обработки. Переменными параметрами экспериментов были объем моторного масла, температура и соленость воды. В каждой серии экспериментов регистрировались два из вышеуказанных параметров, и для разных значений оставшегося параметра измерялась временная зависимость области распространения.

Для устранения случайных ошибок экспериментальные данные были подвергнуты дополнительной обработке с использованием модифицированного алгоритма сдвига (MSA) [8], который показал стабильную производительность при выделении полезного сигнала на фоне шума вплоть до отношения сигнал/шум –15 дБ.

Ниже приведены только самые характерные экспериментальные зависимости из множества измерительных результатов.

На рис. 1 а красными точками показана экспериментальная зависимость площади разлива моторного масла Volga M8B-SAE 20 API от времени. Данные нормируются по своему максимальному значению, черные точки являются результатом обработки набора красных точек алгоритмом MSA. Все последующие экспериментальные данные, представленные здесь, также подвергались обработке алгоритмом MSA.

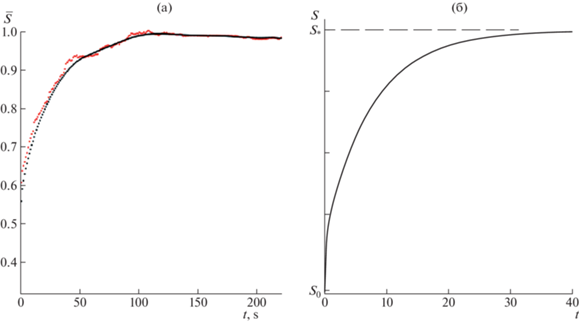
Как можно видеть, поведение кривой $\overline S (t)$ на рис. 1 а хорошо соответствует зависимости (16), проиллюстрированной на рис. 1 (б). Здесь и на рис. 2 б отсчеты времени безразмерны и являются условными, причины чего будут объяснены далее.

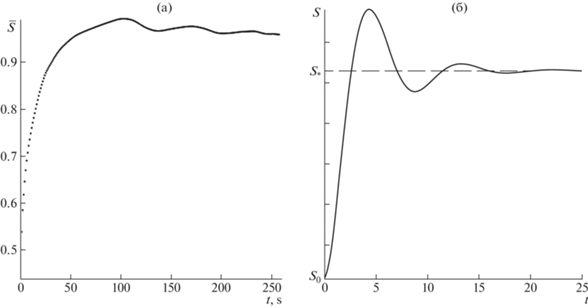
Согласно (16), отклонение от положения равновесия $F = {{F}_{*}}$ описывается двумя убывающими показателями $\exp \left( { - {{a}^{2}}t + \mu t} \right)$ и $\exp \left( { - {{a}^{2}}t - \mu t} \right)$. В начальные моменты времени вклад от члена, содержащего $\exp \left( { - {{a}^{2}}t - \mu t} \right)$, уменьшается наиболее быстро. В последующие моменты времени, когда основной вклад в отклонение вносит член, содержащий $\exp \left( { - {{a}^{2}}t + \mu t} \right)$, скорость снижения отклонения уменьшается по сравнению с начальными моментами времени. Этот факт отражен в поведении кривой на рис. 1 б.

Колебательный режим, описываемый соотношением (15), наблюдался экспериментально на пресной воде $\left( {{{a}^{4}} < {{b}^{2}}} \right)$, и его обработанные данные представлены на рис. 2 а. Разница в поведении ограниченной области разлива на рис. 1 и 2 объясняется тем фактом, что в случае решения (16) скорость перехода кинетической энергии нефтяного топлива в кинетическую энергию воды (из-за явления сопротивления формы) значительно больше, чем скорость перехода к поверхностной энергии на границе раздела контактирующих сред, в отличие от случая решения (15), когда наблюдается обратная корреляция этих скоростей. Сырая нефть демонстрирует иное поведение, связанное с неограниченным разливом углеводородов, экспериментальные данные для которой показаны на рис. 3 а. Поскольку размеры лабораторной установки не позволяют отследить разлив на большой площади и показать ее экспоненциальный рост на больших временах, сравнение с теоретическими результатами (16, 17) проводится только за небольшие промежутки времени от начала процесса. Расчеты, представленные на рис. 3 б, выполненные в соответствии с соотношениями (16, 17), показывают хорошее качественное совпадение эксперимента и теории.

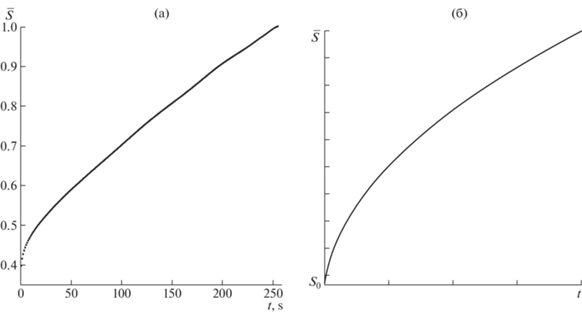
Сравнения экспериментальных и теоретических результатов, представленные в этом разделе, носят исключительно качественный характер из-за недостатка вычислительных данных. Невозможно провести количественное сравнение для всех экспериментальных ситуаций из-за отсутствия некоторых количественных характеристик тестируемых сред. Чтобы доказать этот факт, достаточно привести уравнение (2.41) к безразмерной форме путем введения новых переменных

подстановка, которая в (14) приводит это уравнение к виду

Поведение решений этого однопараметрического уравнения определяется величиной ${{\varepsilon }}$, значение которой задается массой олеина ${{M}_{o}}$, плотностью и вязкими свойствами воды и олеина – коэффициентом ${{\alpha }}$, суммарным поверхностным натяжением ${{\sigma }}$ на линии контакта трех сред и коэффициентом сопротивления формы ${{C}_{{sh}}}$. И если первые три значения известны с достаточной степенью точности, то оценки коэффициента сопротивления формы пятна машинного масла или сырой нефти, разливающейся по воде, в настоящее время неизвестны. Получение таких оценок требует сложных и трудоемких измерений, что является отдельной научной задачей.

Построенная теоретическая модель растекания в виде приближенного уравнения (14), общего как для ограниченной, так и для неограниченной площади разлива олеина, позволила получить явные аналитические решения для любого момента времени процесса, не разделяя его на отдельные временные отрезки, как это было сделано в [2, 3]. В случае, когда характерные свойства среды таковы, что существует предельное состояние в виде пятна олеина конечной площади (соотношения (15, 16)), которое формируется в виде углеводородной линзы [9], и характеризует растекание на его конечной стадии либо затухающими колебаниями (15), либо монотонным достижением предельного значения (16). В первом случае колебательное поведение обусловлено превышающим влиянием сил поверхностного натяжения по сравнению с силой сопротивления формы пятна, а во втором случае имеет место обратное соотношение сил. Если свойства контактирующих сред таковы, что нет предельного размера олеинового пятна, что является следствием превышения коэффициента поверхностного натяжения на границе воздух–вода над суммой коэффициентов на границах вода–олеин и воздух–олеин, то наблюдается неограниченное растекание, площадь которого растет экспоненциально с течением времени (16, 17).

Работоспособность полученного унифицированного уравнения динамики разлива олеина подтверждается сравнением с экспериментальными результатами, которые выявили те же режимы для разных типов олеинов, что и в теоретическом описании.