Доклады Российской академии наук. Науки о Земле, 2023, T. 508, № 2, стр. 258-264

ВВЕДЕНИЕ

При исследовании неустойчивости геосистем особую и чрезвычайно важную роль играет выяснение вопроса о скорости развития неустойчивости.

Как известно, геоматериалы обладают очень большой вязкостью, наличие которой может существенно сказываться на процессах в Земле, и в том числе на процессе развития неустойчивости в неустойчивых геосистемах. Хорошо известно, что для систем, образованных аномально стратифицированными вязкими жидкостями, вязкость замедляет скорость развития неустойчивости, и тем в большей степени, чем она больше. Однако поведение геоматериалов по ряду причин недопустимо отождествлять с поведением вязкой жидкости: помимо того, что это более сложная среда, сочетающая в себе как упругие, так и вязкие свойства, такое отождествление приводит к возникновению неразрешимых внутренних противоречий при теоретическом анализе устойчивого и неустойчивого поведения геосистем. Заметим, что весьма распространенные в геофизическом сообществе представления о характере и динамике процессов в устойчивых геосистемах кардинальным образом отличаются от представлений о характере и динамике процессов в неустойчивых геосистемах. В устойчивых системах такие известные динамические явления, как распространение волн и собственные колебания, исследуются с помощью динамических уравнений теории упругости, основанных на упругих определяющих соотношениях для геоматериалов. В случае неустойчивости возможность применения теории упругости для изучения динамики процессов развития неустойчивости ставится под сомнение на том основании, что в силу очень большой вязкости геоматериалов процесс развития неустойчивости происходит совсем иначе, чем в упругих системах, а именно очень медленно (как в вязких жидкостях). При этом, однако, не учитывается тот факт, что и устойчивые, и неустойчивые геомассивы состоят из одних и тех же геоматериалов, а отождествление геоматериалов с вязкими жидкостями несовместимо с наличием динамических процессов в устойчивых геосистемах. По этой причине нет никаких оснований утверждать априори, что процесс потери устойчивости в геосистемах происходит медленно. Выяснение вопроса о темпе развития неустойчивости является предметом соответствующей задачи механики, в постановке которой должны фигурировать, в числе прочего, особенности принимаемой модели геоматериала.

В предыдущей работе авторов [1] вопрос о темпе развития неустойчивости в неустойчивых вязкоупругих геосистемах был исчерпывающе исследован на предельно простых модельных задачах. В данной работе тот же вопрос исследуется аналитически в рамках соответствующей полноценной трехмерной постановки задачи для геомассива, занимающего ограниченную область пространства с заданными граничными условиями. Полученные аналитические результаты качественно совпадают с результатами, полученными ранее на простых моделях и позволившими выявить существенные закономерности исследуемых процессов.

ИССЛЕДУЕМАЯ МЕХАНИЧЕСКАЯ СИСТЕМА. ПОСТАНОВКА ЗАДАЧИ О РАЗВИТИИ НЕУСТОЙЧИВОСТИ

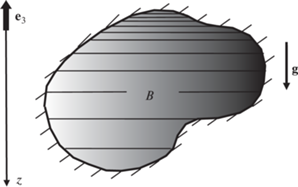
В данной работе рассматриваются аномально стратифицированные по глубине геомассивы, состоящие из несжимаемых вязкоупругих геоматериалов и занимающие области произвольной формы при условии отсутствия смещений на границе (рис. 1). Под стратификацией понимается зависимость плотности и других механических параметров геоматериала от глубины, т.е. от вертикальной координаты $z$, отсчитываемой в направлении силы тяжести. Аномальной считается такая стратификация, при которой плотность уменьшается с глубиной.

При исследовании неустойчивости будет использоваться линеаризованное уравнение импульса совместно с линеаризованным определяющим соотношением в окрестности состояния неустойчивого равновесия. Вывод всех соотношений будет основан на отсчетном описании сплошной среды в сочетании с системой безындексных тензорных обозначений Дж. В. Гиббса. При этом обозначения механических величин принимаются в виде, близком к обозначениям соответствующих величин в книгах [2, 3]. За отсчетную конфигурацию принимается исследуемая на неустойчивость равновесная конфигурация. Принимается также, что поле напряжений в отсчетной конфигурации является гидростатическим. Возмущения напряжений при отклонениях от невозмущенного отсчетного состояния характеризуются, вообще говоря, возможным наличием касательных напряжений (т.е. возможной негидростатичностью). Возмущения напряжений задаются инкрементальными вязкоупругими определяющими соотношениями максвелловского типа для несжимаемой среды.

Зададим ортонормированный базис $\left( {{{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}},{{{\mathbf{e}}}_{3}}} \right)$, причем орт ${{{\mathbf{e}}}_{3}}$ направлен вертикально вверх (рис. 1). Будем считать, что изучаемая механическая система находится в однородном поле силы тяжести, направленном вертикально вниз (${\mathbf{g}} = - g{{{\mathbf{e}}}_{3}}$) и состоит из аномально стратифицированного по глубине несжимаемого вязкоупругого материала, занимающего в исследуемом на устойчивость равновесном состоянии область $B$ произвольной формы.

Пусть ${\mathbf{x}}$ – радиус-вектор материальной точки в отсчетной конфигурации. Запишем радиус-вектор ${\mathbf{r}}$ ее текущего положения в следующем виде: ${\mathbf{r}} = {\mathbf{r}}({\mathbf{x}})$. Отсчетная глубина $z$ задается следующим равенством: $z \equiv - {{{\mathbf{e}}}_{3}} \cdot {\mathbf{x}}$.

Гидростатичность отсчетного равновесного состояния влечет за собой стратификацию отсчетной плотности и отсчетного давления по отсчетной глубине $z$:

Будем считать, что и параметры, задающие вязкоупругие свойства материала (т.е. коэффициент вязкости и упругие модули, входящие в инкрементальное определяющее соотношение) также стратифицированы по глубине.

В отсчетном описании уравнение импульса записывается с помощью тензора напряжений Пиолы ${{{\mathbf{T}}}_{\kappa }}$, в то время как инкрементальное определяющее соотношение вязкоупругости изначально записывается в терминах тензора напряжений Коши ${\mathbf{T}}$. Связь между этими тензорами выражается известным соотношением [2, 3]:

где ${{\nabla }_{\kappa }}$ означает градиент по ${\mathbf{x}}$. В силу предположения о несжимаемости материала $\det {\mathbf{F}}({\mathbf{x}},t)$ = 1.

В отсчетной конфигурации ${\mathbf{r}}({\mathbf{x}}) = {\mathbf{x}}$, ${\mathbf{F}}({\mathbf{x}}) = {\mathbf{I}}$, ${{{\mathbf{T}}}_{\kappa }}\left| {_{{{\mathbf{F}} = {\mathbf{I}}}}} \right. \equiv {{{\mathbf{T}}}_{{{{\kappa }_{0}}}}}$ = ${{{\mathbf{T}}}_{0}}$ = $ - {{p}_{0}}(z){\mathbf{I}}$, где I – единичный тензор второго ранга (ТР(2)). В текущей конфигурации ${\mathbf{T}}({\mathbf{x}},t)$ = ${{{\mathbf{T}}}^{d}}({\mathbf{x}},t)$ – $p({\mathbf{x}},t){\mathbf{I}}$, где ${{{\mathbf{T}}}^{d}}({\mathbf{x}},t)$ – девиатор напряжений, ${{{\mathbf{T}}}^{d}}({\mathbf{x}},0) = 0$, p(x, t) – давление.

Уравнения импульса в текущей и отсчетной конфигурациях дают:

где точка над символом означает материальную (т.е. при ${\mathbf{x}} = \operatorname{const} $) производную по времени. Введем следующие обозначения для возмущений:

При линеаризации всех соотношений по $\delta {\mathbf{F}}$ получим:

Уравнение импульса в возмущениях принимает следующий вид:

Линейное вязкоупругое определяющее соотношение максвелловского типа [4] для несжимаемого материала зададим в следующем виде:

где тензор четвертого ранга (ТР(4)) ${\mathbf{L}}(z)$ – тензор упругих модулей для напряжений Коши, относящийся к материалу соответствующей упругой системы сравнения (УСС), $\chi (z)$ – коэффициент вязкости. Тензор ${\mathbf{L}}$ отображает симметричные девиаторы второго ранга в симметричные девиаторы второго ранга; помимо этого, в силу гидростатичности невозмущенного поля напряжений, ТР(4) ${\mathbf{L}}$ симметричен в отношении действия на ТР(2): ${{{\mathbf{H}}}_{1}}:{\mathbf{L}}:{{{\mathbf{H}}}_{2}}$ = ${{{\mathbf{H}}}_{2}}:{\mathbf{L}}:{{{\mathbf{H}}}_{1}}$, $\forall {{{\mathbf{H}}}_{1}},{{{\mathbf{H}}}_{2}}$.

Будем считать также, что ${\mathbf{L}}$ положительно определен: ${\mathbf{H}}:{\mathbf{L}}:{\mathbf{H}} > 0$, $\forall {\mathbf{H}} \ne 0$. Тогда, в силу спектральной теоремы для ТР(4) [5], для него справедливо следующее спектральное разложение:

Для ортогонального проектора ${{{\mathbf{1}}}^{{{\text{dev}}}}}$ на подпространство симметричных девиаторов имеем:

Будем искать решение системы линейных уравнений (6), (7) в виде экспоненциальной зависимости от времени:

В этом случае уравнение (7) становится алгебраическим и может быть разрешено относительно $\delta {{{\mathbf{T}}}^{d}}({\mathbf{x}})$:

Заметим, что

Уравнение импульса (6), условие несжимаемости и граничное условие таковы:

Будем искать решения линейных уравнений (14), (15) для вещественных положительных значений $\lambda $, т.е. экспоненциально нарастающие решения с инкрементом нарастания $\lambda > 0$. В этом случае все ТР(4) ${\mathbf{\tilde {L}}}(z)$ симметричны, при $\lambda > 0$ они положительно определены (${\mathbf{H}}:{\mathbf{\tilde {L}}}:{\mathbf{H}} > 0$, $\forall {\mathbf{H}} \ne 0$), и квадратичная форма ${\mathbf{H}}:{\mathbf{\tilde {L}}}:{\mathbf{H}}$ монотонно возрастает от нуля до ${\mathbf{H}}:{\mathbf{L}}:{\mathbf{H}}$ при изменении $\lambda $ от нуля до $ + \infty $.

Покажем, что оператор $\tilde {\mathcal{A}}\left( {\lambda {\text{,}}\left\{ {\delta {\mathbf{r}}} \right\}} \right)$ на подпространстве соленоидальных полей $\delta {\mathbf{r}}({\mathbf{x}})$, обращающихся в нуль на границе области, для любого $\lambda $ симметричен относительно интегрального [11, 12] скалярного произведения ${{\left\langle {{{{\mathbf{w}}}_{1}} \cdot {{{\mathbf{w}}}_{2}}} \right\rangle }_{B}}$, т.е.

Для этого преобразуем подынтегральное выражение в левой части равенства (16):

Учитывая, что дивергентные слагаемые в силу граничных условий при интегрировании дают ноль, а ${{\nabla }_{\kappa }}{{\rho }_{\kappa }} = - {{{\mathbf{e}}}_{3}}\frac{{d{{\rho }_{\kappa }}}}{{dz}}$, получаем выражение, симметрия которого очевидна:

Учитывая предположение об аномальной стратификации, в силу которого $ - \frac{{d{{\rho }_{\kappa }}}}{{dz}} = \left| {\frac{{d{{\rho }_{\kappa }}}}{{dz}}} \right|$, для соответствующего квадратичного функционала $\Psi \left( {\lambda {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$ получаем:

При $\lambda = \infty $ имеем: ${\mathbf{\tilde {L}}}(\infty ) = {\mathbf{L}}$, а функционал $\Psi \left( {\infty {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$ = $ - R\left\{ {\mathbf{w}} \right\}$, где $R\left\{ {\mathbf{w}} \right\}$ – вторая вариация полной потенциальной энергии (ППЭ) соответствующей УСС. Если УСС устойчива, то функционал $R\left\{ {\mathbf{w}} \right\}$ положительно определен, а если УСС неустойчива, то на некотором подмножестве кинематически допустимых полей ${\mathbf{w}}({\mathbf{x}})$ функционал $R\left\{ {\mathbf{w}} \right\}$ принимает отрицательные значения.

Поскольку ${\mathbf{\tilde {L}}}(0) = {\mathbf{0}}$, то при $\lambda = 0$ второе слагаемое в выражении для $\Psi $ пропадает и $ - \Psi \left( {0{\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$ < < 0 – вторая вариация ППЭ для несжимаемой аномально стратифицированной идеальной жидкости, которая заведомо неустойчива.

Уравнение (14) выражает тот факт, что искомые поля $\delta {\mathbf{r}}({\mathbf{x}})$ (в дальнейшем обозначаемые ${\mathbf{w}}({\mathbf{x}})$) являются обобщенными собственными функциями (ОСФ) с весом ${{\rho }_{\kappa }}({\mathbf{x}})$ симметричного линейного оператора $\tilde {\mathcal{A}}\left( {\lambda {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$, а числа ${{\lambda }^{2}}$ являются соответствующими обобщенными собственными числами (ОСЧ). Заметим, что при любом $\lambda > 0$ оператор $\tilde {\mathcal{A}}\left( {\lambda {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$ имеет некоторый зависящий от $\lambda $ набор ОСЧ, однако эти ОСЧ, вообще говоря, не равны ${{\lambda }^{2}}$, что требовалось бы для выполнения уравнения (14). Для нахождения искомых значений $\lambda $ (из которых нас интересует наибольшее значение) будем изучать обобщенный спектр оператора $\tilde {\mathcal{A}}\left( {\lambda {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$ для всевозможных значений $\lambda > 0$.

В силу рассуждений, совершенно аналогичных таковым при анализе собственных колебаний упругих тел, с использованием симметрии оператора $\tilde {\mathcal{A}}\left( {\lambda {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$, полуограниченности сверху квадратичного функционала $\Psi \left( {\lambda {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$, а также в силу леммы Реллиха [6], получаем следующие спектральные свойства данного оператора при $\lambda > 0$:

1) оператор имеет дискретный набор ОСЧ ${{\beta }_{i}}(\lambda )$, $i = 1,\;2,...$, с весом ${{\rho }_{\kappa }}({\mathbf{x}})$, ограниченный сверху, причем ОСЧ ${{\beta }_{i}}(\lambda )\;$ занумерованы в порядке невозрастания $\left( {{{\beta }_{{i + 1}}}(\lambda ) \leqslant {{\beta }_{i}}(\lambda )} \right)$;

2) ОСЧ соответствует набор ОСФ ${{{\mathbf{w}}}_{i}}(\lambda ,{\mathbf{x}})$, ортонормированный относительно положительно определенного билинейного функционала ${{\left\langle {{{\rho }_{\kappa }}{{{\mathbf{w}}}_{i}} \cdot {{{\mathbf{w}}}_{j}}} \right\rangle }_{B}}$:

Тогда задача нахождения возможных инкрементов нарастания для форм потери устойчивости сводится к нахождению таких вещественных положительных значений ${{\lambda }_{i}}$, для которых выполняется равенство

причем интерес представляет наибольшее из таких значений ${{\lambda }_{*}}$:

При анализе уравнений (19) будем отдельно рассматривать свойства левой части равенства (равной ${{\lambda }^{2}}$) и свойства правых частей ${{\beta }_{i}}(\lambda )$ как функций $\lambda \;$. Левые части монотонно возрастают от нуля до $ + \infty $. Покажем, что правые части монотонно убывают при изменении $\lambda \;$ от нуля до $ + \infty $, причем предельные значения при $\lambda \; \to 0$ (что соответствует аномально стратифицированной идеальной жидкости) положительные. Действительно, для любого ${\mathbf{w}}({\mathbf{x}})$ функция $\Psi \left( {\lambda {\text{,}}\left\{ {\mathbf{w}} \right\}} \right)$ монотонно убывает, т.к. квадратичная форма ${\mathbf{H}}:{\mathbf{\tilde {L}}}:{\mathbf{H}}$ монотонно возрастает от нуля и до ${\mathbf{H}}:{\mathbf{L}}:{\mathbf{H}}$. Тогда из известной теоремы сравнения [6] следует и монотонное убывание всех ОСЧ.

Сначала исследуем уравнение (19) для наибольшего ОСЧ ${{\beta }_{1}}(\lambda )$ с ОСФ ${{{\mathbf{w}}}_{1}}({\mathbf{x}},\lambda )$, которые характеризуются следующим вариационным принципом:

Заметим, что при $\lambda \; = 0$ супремум существует, но ни на какой экстремали не достигается:

Здесь $\gamma _{0}^{{}}$ – наибольший (предельный) инкремент нарастания возмущений для аномально стратифицированной несжимаемой жидкости.

ОСЧ ${{\beta }_{1}}(\infty )$ соответствует УСС, а знак ${{\beta }_{1}}(\infty )$ зависит от того, является ли она устойчивой или неустойчивой. Если УСС устойчива, то, в соответствии с известным вариационным принципом для собственных колебаний упругих тел [6], имеем:

где $\underline \omega $ – наименьшая (“основная”) частота собственных колебаний. Если же УСС неустойчива, то где $\gamma $ – наибольший инкремент нарастания возмущений для неустойчивой УСС (совершенно аналогично вариационному принципу для собственных колебаний).

В силу монотонного возрастания ${{\lambda }^{2}}$ и монотонного убывания ${{\beta }_{i}}(\lambda )$, с учетом того, что интерес представляет наибольшее значение $\lambda $, при котором выполняется какое-либо из уравнений (19), достаточно исследовать это уравнение для наибольшего из ОСЧ, т.е. для ${{\beta }_{1}}(\lambda )$, поскольку для меньших ОСЧ уравнение будет выполняться при меньших значениях $\lambda $. Будем исследовать уравнение (19) отдельно для случаев неустойчивости и устойчивости УСС.

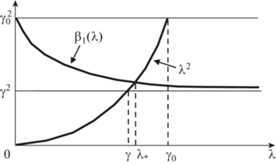
Неустойчивая УСС. Функция ${{\beta }_{1}}(\lambda )$ положительна, ${{\beta }_{1}}(0) = \gamma _{0}^{2}$, ${{\beta }_{1}}(\infty ) = {{\gamma }^{2}}$, и ${{\beta }_{1}}(\lambda )$ монотонно убывает от $\gamma _{0}^{2}$ до ${{\gamma }^{2}}$ (рис. 2). Значит, уравнение ${{\lambda }^{2}} = {{\beta }_{1}}(\lambda )$ имеет единственное решение ${{\lambda }_{*}} \in (\gamma ,{{\gamma }_{0}})$. Заметим, что при любой вязкости ${{\lambda }_{*}} > \gamma $, т.е. соответствующая мода потери устойчивости нарастает быстрее, чем наибыстрейшая мода для неустойчивой УСС.

При $\lambda > {{\lambda }_{*}}$ имеем: ${{\beta }_{1}}(\lambda ) < {{\lambda }^{2}}$, следовательно, ${{\lambda }_{*}}$ – наибольший инкремент нарастания для всех мод потери устойчивости, причем ${{\lambda }_{*}} \to \gamma $ при $\chi \to \infty $.

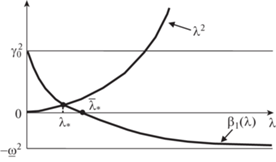
Устойчивая УСС. В этом случае ${{\beta }_{1}}(\lambda )$ остается монотонно убывающей функцией, ${{\beta }_{1}}(0) = \gamma _{0}^{2} > 0$, ${{\beta }_{1}}(\infty ) = - {{\underline \omega }^{2}} < 0$ (рис. 3), где $\underline \omega $ – наименьшая частота собственных колебаний УСС. Как и в случае неустойчивой УСС, уравнение ${{\lambda }^{2}} = {{\beta }_{1}}(\lambda )$ имеет единственное решение ${{\lambda }_{*}}$, для которого получены двусторонние оценки ${{\underline \lambda }_{*}} < {{\lambda }_{*}} < {{\bar {\lambda }}_{*}}$:

${{\underline \gamma }_{0}} < {{\gamma }_{0}}$, $\bar {\tau } \equiv \frac{{\bar {\chi }}}{{\underline \mu }}$, $\underline \tau \equiv \frac{{\bar {\chi }}}{{\bar {\mu }}}$, где $\bar {\tau }$ и $\underline \tau $ – “верхнее” и “нижнее” времена релаксации.

В случае большой вязкости (и больших времен релаксации) для ${{\underline \lambda }_{*}}$ имеется следующая асимптотика:

Из равенств (25), (26) очевидно, что в случае устойчивости УСС ${{\underline \lambda }_{*}}$ и ${{\bar {\lambda }}_{*}}$ стремятся к нулю при стремлении вязкости к бесконечности, из чего следует, что ${{\lambda }_{*}}$ тоже стремится к нулю.

ЗАКЛЮЧЕНИЕ

В геофизической литературе рассматриваются различные механизмы движения геомасс, приводящие к образованию новых геоструктур: медленные процессы мантийной конвекции, тектоника плит, образование плюмов, являющихся, как считается, причиной вулканической активности, и ряд других [7].

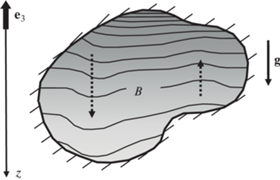
В данной работе в рамках максвелловской вязкоупругой модели геоматериалов и в полноценной трехмерной постановке впервые теоретически исследован еще один (в принципе, давно известный) механизм зарождения новых геоструктур, а именно, процесс ухода от положения неустойчивого равновесия в аномально стратифицированном геомассиве (рис. 4). При этом обнаружено, что существуют два принципиально различных вида таких процессов. Один имеет место для вязкоупругих геомассивов с устойчивой УСС. Такие массивы неустойчивы, однако развитие их неустойчивости из-за наличия вязкости идет медленно, и тем медленнее, чем больше вязкость (что согласуется с традиционными представлениями о влиянии вязкости на темп протекания процессов); при очень большой вязкости такая неустойчивость почти незаметна. Другой вид процесса ухода от положения равновесия имеет место для вязкоупругих геомассивов с неустойчивой УСС. Они не только неустойчивы, но еще и “динамически” неустойчивы: скорость нарастания основной (т.е. наибыстрейшей) формы потери устойчивости всегда выше, чем для соответствующей УСС. Заметим, что геомассив с изначально устойчивой УСС может превратиться в таковой с неустойчивой УСС вследствие уменьшения сдвиговых жесткостей геоматериалов. Такое уменьшение может произойти по разным причинам; к нему могут привести, например, изменение температуры или химические превращения в слагающих геомассив породах. В результате геомассив, деформирование которого было почти незаметно на протяжении длительного промежутка времени, может внезапно оказаться подверженным быстрым перестройкам. При этом, как бы ни была велика вязкость материалов, слагающих такой геомассив, уход от положения равновесия будет идти быстрее, чем в УСС. Из этого можно сделать вывод, что на больших глубинах, где, как известно, вязкость огромна [8], процессы развития неустойчивости могут протекать динамически (как в неустойчивой упругой системе). В частности, этим подтверждается полная применимость к реальным геосистемам полученных ранее авторами [9–12] результатов исследования вопросов устойчивости стратифицированных упругих геосистем.

Полученные в работе теоретические результаты могут послужить основой как для объяснения тех или иных закономерностей в истории развития Земли, так и для интерпретации получаемых геофизических данных и выяснения причин динамических процессов, происходящих в Земле в настоящее время.