1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 4, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 4, стр. 462-472

Динамика биотических потоков углерода при различных сценариях изменения площади лесов

В. В. Клименко a, *, О. В. Микушина a, А. Г. Терешин a

a Национальный исследовательский университет “МЭИ”
111250 Москва, Красноказарменная ул., 14, Россия

* E-mail: nilgpe@mpei.ru

Поступила в редакцию 08.08.2019
После доработки 03.02.2020
Принята к публикации 05.02.2020

Полный текст (PDF)

Аннотация

В работе представлена оценка глобальных биотических потоков углерода в атмосферу при различных сценариях изменения площади лесов в умеренно-бореальной и тропической зонах. Для формирования сценариев лесопользования были привлечены данные последних десятилетий как национальных инвентаризаций лесных земель, так и различные оценки площадей поверхности планеты, покрытой древесной растительностью, полученные по данным дистанционного зондирования Земли. Предложено три новых сценария изменения площади умеренно-бореальных лесов – их увеличения FAOSTAT (основанный на данных инвентаризаций), а также сохранения на современном уровне CONST и постепенного сведения LANDSAT (согласно спутниковым данным из разных источников). Для сценариев FAOSTAT и LANDSAT сохраняется тенденция сведения тропических лесов. Указанные сценарии, а также опубликованный ранее авторский базовый сценарий GEPL97 были использованы для получения модельных биотических потоков углерода. Разработанная в МЭИ и недавно обновленная модель углеродного цикла, учитывающая антропогенную эмиссию углерода, как индустриальную, так и связанную со сведением лесов и землепользованием, позволила обстоятельно проследить и проанализировать вероятную динамику биотических источников и стоков углерода. Показано, что абсолютная величина биотических потоков углерода в атмосферу, а также их знак существенно зависит от принятого сценария – от сохранения в текущем столетии биосферы как эффективного стока избыточного углерода из атмосферы (GEPL97, CONST) до превращения ее в дополнительный источник CO2 (LANDSAT). Сценарий FAOSTAT приводит в 2100 г. к возвращению биотических потоков на современный уровень. Максимальное различие нетто-потоков углерода из биосферы в атмосферу для рассмотренных сценариев составляет почти 2.5 Гт C/год и приходится примерно на середину текущего столетия. Разность между соответствующими значениями концентрации CO2 для рассмотренных сценариев изменения площади лесов достигает к 2100 г. 65 млн–1.

Ключевые слова: модель углеродного цикла, биотические источники и стоки углерода, изменение площади лесов, нетто-поток, дефорестация, рефорестация, сценарии, концентрация углекислого газа

1. ВВЕДЕНИЕ

Сведение лесов в целях обустройства пахотных земель и пастбищ, а также для заготовки топлива и строительных материалов – это значительное антропогенное вмешательство в природу с серьезными последствиями для глобального климата и экологии. Обезлесение приводит к увеличению содержания углекислого газа в атмосфере, росту глобальной температуры и значительной трансформации полей осадков. Заметное нарастание концентрации CO2 в атмосфере, связанное почти исключительно с вырубкой лесов и их последующим сжиганием, имело место уже в первой половине XIX-го века. В индустриальный период на значительно возросшие биотические потоки углерода в атмосферу был наложен мощный промышленный выброс углекислого газа связанный со сжиганием органического топлива. К концу XX-го века в результате сложения многих факторов, в том числе антропогенного восстановления лесов умеренного и бореального поясов и т.н. обратных связей, действующих в условиях повышения концентрации СО2 и роста температуры (расширение площадей, занимаемых континентальной биотой, возрастание фиксации атмосферного углерода растениями и др.), биотический нетто-поток углерода в атмосферу начал заметно снижаться [1]. От того, насколько устойчив нынешний тренд, в значительной мере зависят будущие концентрации СО2, а с ними также масштаб ожидаемых климатических изменений и реакция на них мирового сообщества.

2. МОДЕЛЬ ГЛОБАЛЬНОГО УГЛЕРОДНОГО ЦИКЛА

Основным инструментом исследования потоков углерода между атмосферой, океаном и биосферой являются модели глобального углеродного цикла [2, 3], в настоящее время они обычно сопряжены с климатическими моделями, образуя т.н. модели земной системы [4–6]. Наиболее сложным резервуаром углерода, вносящим большую неопределенность в его глобальный баланс, является наземная растительность [3, 4], и, в первую очередь, леса [7, 8]. Для России вопрос корректной оценки эмиссии и стока углерода в лесную растительность стоит особенно остро – при подготовке Парижского соглашения (2015 г.) сторон РКИК ООН наша страна поставила условием выполнения своих обязательств по сокращению выбросов парниковых газов “максимально возможный учет поглощающей способности лесов” [9]. Для изучения процессов накопления и эмиссии углерода из лесных экосистем разработаны специальные модели различной сложности [10, 11].

Целью настоящей работы является проверка работоспособности разработанной в МЭИ модели углеродного цикла (см. приложение) на основе широкого спектра данных наблюдений за динамикой лесного резервуара, выполненных в течение последних трех десятилетий. Для корректного моделирования биотических потоков углерода в работах [12–14] был разработан пятикомпонентный биосферный блок, в котором, в частности, рассчитываются потоки углерода в атмосферу за счет дефорестации и изменений в землепользовании, учитывается увеличение биопродуктивности растений при повышении атмосферной концентрации CO2 и рост занимаемых наземной биотой площадей в условиях развития глобального потепления. Внешним возмущением стационарных потоков модели является антропогенная эмиссия углерода, как индустриальная, так и связанная со сведением лесов и землепользованием. Модель углеродного цикла, основным назначением которой является прогноз атмосферных концентраций CO2, дает возможность также обстоятельно проследить и проанализировать динамику биотических источников и стоков углерода.

Модель зарекомендовала себя успешным инструментом прогноза атмосферных концентраций СО2, с неизменными исходными параметрами, демонстрируя в течение последних 25 лет не превышающую 2 млн–1 разницу расчетных данных и данных глобального мониторинга [2, 15]. Тем не менее, по мере накопления данных, касающихся поведения и взаимодействия различных резервуаров углерода, было сочтено необходимым провести ревизию некоторых параметров модели: коэффициента турбулентной диффузии в глубоком океане (K), относительной площади соприкосновения глубинных вод с атмосферой (ac), коэффициента (λ) соотношения стационарных потоков атмосфера–слой перемешивания и атмосфера–океан в полярных широтах, коэффициента равновесного изменения массы долгоживущей биоты (kw), приходящегося на изменение глобальной температуры в 1°C, коэффициента увеличения биопродуктивности (γ) при удвоении атмосферной концентрации СО2. Значения этих параметров перечислены в табл. 1.

Таблица 1.  

Варианты значений параметров действующей модели глобального цикла углерода

Вариант ac λ K (м2/год) kw (Гт /oC) γ
Середина 1990-х 0.065 1.70 2610 32.3 0.20
Конец 2010-х 0.150 0.25 3531 52.0 0.28

Изменение массы углерода в долгоживущей биоте, соответствующее температурному изменению при сдвиге границ экосистем, вычисляется по формуле:

(1)
${{N}_{T}}\left( t \right) = {{k}_{W}}\left( {T\left( {t - {\text{lag}}} \right) - {{T}^{0}}} \right),~$
где T(t) – сглаженная среднеглобальная температура, lag = 24 года – время запаздывания сдвига границ (соответствует времени реакции лесов бореальной зоны), ${{T}^{0}}$ – доиндустриальное значение температуры. Поскольку$~{{N}_{T}}\left( t \right)~$ по определению в модели связано исключительно с изменением площади S долгоживущей биоты (главным образом, лесов), имеем
(2)
$\frac{{{{S}_{T}}\left( t \right)}}{{{{S}_{0}}}} = \frac{{{{N}_{T}}\left( t \right)}}{{N_{W}^{0}}} = \frac{{{{k}_{W}}\left( {T\left( {t - {\text{lag}}} \right) - {{T}^{0}}} \right)}}{{N_{W}^{0}}},$
где $N_{W}^{0} = $ 480 Гт С – доиндустриальное содержание углерода в долгоживущей биоте.

Используемое ранее значение kw было скорректировано в связи с вновь полученными результатами реконструкции климата голоцена [16], из которых следует, что абсолютный максимум повышения температуры был достигнут около 5 тыс. лет до н. э. и был на 0.65°C выше климатической нормы середины XX в., а средняя за самое теплое тысячелетие (6.5–5.5 тыс. лет т.н.) аномалия температуры составляла 0.60°C.

Удельное содержание углерода в долгоживущей биоте ${{b}_{W}}\left( t \right)$ рассчитывается в модели как линейная функция атмосферной концентрации CO2:

(3)
${{b}_{W}}\left( t \right) = {{b}_{0}}\left( {1 + \gamma {{\nu }_{a}}\left( t \right)} \right),~$
где b0 – доиндустриальное среднеинтегральное содержание углерода в долгоживущей биоте, νa(t) – изменение содержания углерода в атмосфере относительно доиндустриального уровня, а γ – коэффициент увеличения биопродуктивности при удвоении атмосферной концентрации CO2.Теперь мы используем более высокое, чем в [12–14], значение γ = 0.28, выбор которого основан на материалах, полученных в последние двадцать лет и обобщенных в [2, 17].

3. ИСТОЧНИКИ ДАННЫХ О ЛЕСАХ

До начала детальных исследований земной поверхности из космоса единственным источником сведений о глобальной структуре земного покрова и землепользования было обобщение данных национальных инвентаризаций. С 1947 года этим занимается Организация по продовольствию и сельскому хозяйству ООН (FAO), в которую из всех стран-участниц ООН регулярно поступает информация в области сельского, лесного и рыбного хозяйства, а также перерабатывающей и пищевой промышленности.

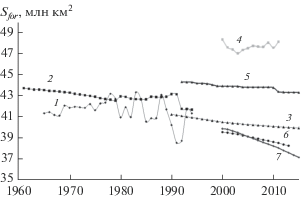
В вышедших в 1947–1998 гг. ежегодниках FAO Production Yearbook [18] отражалась информация об использовании земель в более чем 200 странах мира, в том числе о площадях обрабатываемых земель (в т.ч. пашен) и лесов. Также сведения (начиная с 1961 г.) содержались и в первой версии базы данных FAOSTAT [19], которую эта организация поддерживала в 1990-х годах. Из-за значительных трудностей учета лесных ресурсов, особенно в больших странах, связанных с наличием огромных малонаселенных пространств и невозможностью их детального обследования лесными службами, а также по причине периодической смены методики обработки исходных данных в самой FAO временные ряды мировой лесной статистики для 1961–1994 гг. характеризуются существенной неоднородностью (см. рис. 1).

Рис. 1.

Площадь лесов в мире S по данным лесного хозяйства – ежегодники FAO [18] (1); баз данных FAOSTAT [19] (2) и [20] (3), и данные ДЗЗ о площади древесного покрова MODIS [19] (4), CCI-LC [19] (5), LandSat [27] (6) и [28] (7).

В новой версии базы данных FAOSTAT [19] данные по площадям лесов начинаются с 1990 г. (рис. 1). Кроме того, с 2001 г. FAO каждые пять лет публикует обзоры состояния мировых лесных ресурсов [20], анализируя динамику изменения площадей лесов в мире начиная с 1990 г. [21].

С начала 1970-х годов ведется съемка земной поверхности высокого разрешения в различных спектральных областях и разрабатываются системы распознавания снимков и классификации типов подстилающей поверхности [22]. С середины 1980-х появляются данные расшифровки результатов дистанционного зондирования Земли (ДЗЗ) [23], которые в настоящее время являются одним из основных источников сведений о биогеохимических изменениях на планете [24].

По результатам этих наблюдений сформировано несколько глобальных временных рядов изменения площади лесов, в том числе используемые в настоящей работе:

• FAOSTAT MODIS (2001–2012), содержащий данные по типам земной поверхности в разрезе стран и регионов FAO, рассчитанные по массивам данных измерений спектрорадиометра MODIS, установленного на спутнике Terra Национального управления по аэронавтике и исследованию космического пространства (NASA), сформированных в рамках Международной программы изучения геосферы и биосферы (IGBP) [25].

• FAOSTAT CCI-LC (1992–2015) – аналогичные данные, рассчитанные по снимкам спектрометра MERIS (спутник EnviSat Европейского космического агентства (ESA), 2003–2012), радиометров AVHRR (метеорологические спутники Национального управления исследованиями атмосферы и океана (NOAA), 1992–1999), камер VGT-1 и VGT-2 (европейские спутники SPOT-4 и SPOT-5, 1999–2013) и VGT-P (европейский спутник PROBA-V – с 2013 года) в рамках Программы ESA “ClimateChangeInitiative” [26].

• LandSat (2000–2016), представляющий оценки площадей, покрытой древесной растительностью по данным расшифровки снимков земной поверхности спутниковой программы LandSat (NASA) [27, 28].

Как видно из рис. 1, несмотря на принципиальные различия в используемых методах оценки, все перечисленные временные ряды описывают тенденцию уменьшения лесного покрова планеты. Более того, оценки FAO и результаты спутниковых наблюдений согласуются даже в темпах сокращения площади лесов – примерно 1 млн км2 за 25 лет.

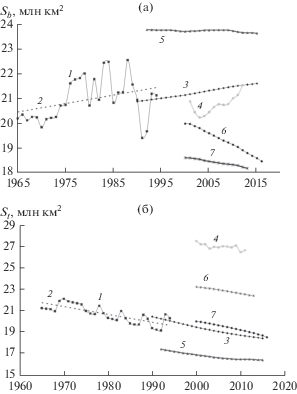
Однако для различных природно-климатических зон (леса бореального и умеренного пояса и тропические леса, сгруппированные по странам в соответствии с рекомендациями FAO) различия более существенны (рис. 2).

Рис. 2.

Площадь бореальных и умеренных Sb (а) и тропических St (б) лесов в мире по данным лесного хозяйства – ежегодников FAO [18] (1) (и линейный тренд 2), базы данных FAOSTAT [19] (3), и данные ДЗЗ о площади древесного покрова MODIS [19] (4), CCI-LC [19] (5), LandSat [27] (6) и [28] (7).

Если для тропических лесов все оценки дают сходную картину уменьшения их площади, то для бореальных и умеренных лесов для периода последних десятилетий представлены три резко различающихся варианта:

1) по результатам обработки FAO данных национальных инвентаризаций наземных наблюдений [19], площадь бореальных и умеренных лесов в 1990–2016 гг. продолжает увеличиваться, причем с той же скоростью, что была зафиксирована в неоднородных данных 1965–1994 гг. (примерно 0.7 млн км2 за 25 лет, или 30 тыс. км2/год);

2) согласно обобщенному ряду спутниковых наблюдений CCI-LC [26], их площадь в 1992–2015 гг. была практически неизменной;

3) и, наконец, данные дистанционного зондирования LandSat свидетельствуют в пользу сокращения этой группы лесов, причем последняя оценка [27] дает скорость уменьшения их площади значительно (более чем в три раза!!) выше, чем более ранняя работа тех же авторов [28].

Справедливости ради следует отметить, что основные расхождения в оценках площади лесов относятся к труднодоступным регионам Сибири и Канады, слабо охваченным службами наземного и воздушного наблюдения. Одной из причин этих расхождений может быть недооценка гибели лесов за счет пожаров, а также неучтенных вырубок (особенно на территории России).

4. ИЗМЕНЕНИЕ ПЛОЩАДИ ЛЕСОВ С 1800 г. И СЦЕНАРИИ ДО 2100 г.

В [13] мы отмечали, что период наиболее интенсивного использования умеренно-бореальных лесов с целью расширения площадей обрабатываемых земель, заготовки древесины, подготовки площадей под гидростроительство продолжался примерно 160 лет – с начала индустриальной эпохи до 1960 г. После этого началось их постепенное восстановление, которое происходит как вследствие аффорестации (искусственных посадок), так и за счет рефорестации, т.е. естественного прироста при потеплении и сдвиге границы между лесами и тундрой. В базовом сценарии изменения площадей лесов [13] предполагалось, что тенденция к сведению тропических лесов тоже будет постепенно остановлена, и начнется их восстановление.

4.1. Относительное изменение площади лесов и поток углерода в атмосферу за счет лесов в 1800–1990 гг.

В модели предполагается, что две трети от общего потока углерода, выбывающего из биосферы за счет дефорестации в данном году, быстро окисляется и выбрасывается в атмосферу (поток Fdef) в том же самом году, а одна треть от этого потока, согласно данным статистики мировой лесной промышленности [18, 19], попадает в продукты длительной консервации с характерным временем оборота около 500 лет. В качестве исходных данных для вычисления площадей вырубки лесов с 1800 до 1960 г., также как и в [12–14], будем использовать значения антропогенного потока Fdef углерода в атмосферу (Гт C/год) за счет дефорестации, вычисленного по данным мощности биотического источника, которые приводятся в [29, 30] без учета возможных обратных связей в системе биосфера–атмосфера–климат. Полагая время запаздывания между вырубкой и выбросом углерода в атмосферу равным τW/2, где τW – характерное время оборота долгоживущей биоты, τW =26 лет, введем поправочный множитель для вычисления реального потока дефорестации $F_{{def}}^{{act}}\left( t \right)$ с учетом изменения биопродуктивности, так как исходные величины Fdef из [29, 30] соответствуют значениям, которые имели бы место при bW (t1980):

(4)
$\begin{gathered} F_{{def}}^{{act}}\left( t \right) = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}S_{{def}}^{{act}}\left( t \right){{b}_{W}}\left( {t - {{{{\tau }_{W}}} \mathord{\left/ {\vphantom {{{{\tau }_{W}}} 2}} \right. \kern-0em} 2}} \right) = \\ = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}S_{{def}}^{{act}}\left( t \right){{b}_{0}}\left( {1 + \gamma {{\nu }_{a}}\left( {t - {{{{\tau }_{W}}} \mathord{\left/ {\vphantom {{{{\tau }_{W}}} 2}} \right. \kern-0em} 2}} \right)} \right) = \\ = \frac{{1 + \gamma {{\nu }_{a}}\left( {t - {{{{\tau }_{W}}} \mathord{\left/ {\vphantom {{{{\tau }_{W}}} 2}} \right. \kern-0em} 2}} \right)}}{{1 + \gamma {{\nu }_{a}}\left( {{{t}_{{1980}}}} \right)}}{{F}_{{def}}}\left( t \right),{\text{\;}} \\ \end{gathered} $
где $S_{{def}}^{{act}}\left( t \right)$ – площадь вырубки, соответствующая потоку $F_{{def}}^{{act}}\left( t \right)$. Обозначая через S0 площадь, занимаемую лесами в доиндустриальный период, имеем

(5)
$\frac{{S_{{def}}^{{act}}\left( t \right)}}{{{{S}_{0}}}} = \frac{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}F_{{def}}^{{act}}\left( t \right)}}{{{{S}_{0}}{{b}_{W}}\left( {t - {{{{\tau }_{W}}} \mathord{\left/ {\vphantom {{{{\tau }_{W}}} 2}} \right. \kern-0em} 2}} \right)}} = \frac{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}{{F}_{{def}}}\left( t \right)}}{{{{b}_{0}}{{S}_{0}}\left( {1 + \gamma {{\nu }_{a}}\left( {{{t}_{{1980}}}} \right)} \right)}}.{\text{\;}}$

Общая площадь вырубки с момента времени t0 (начало индустриальной эпохи) до момента t может быть вычислена как ${{S}_{{def}}}\left( t \right) = \int_{{{t}_{0}}}^t {S_{{def}}^{{act}}} \left( \tau \right)d\tau ,~$ откуда, учитывая $N_{W}^{0} = {{b}_{0}}{{S}_{0}},$ получаем:

(6)
$\frac{{{{S}_{{def}}}\left( t \right)}}{{{{S}_{0}}}} = \frac{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}\int\limits_{{{t}_{0}}}^t {{{F}_{{def}}}} \left( \tau \right)d\tau }}{{N_{W}^{0}\left( {1 + \gamma {{\nu }_{a}}\left( {{{t}_{{1980}}}} \right)} \right)}}.~$

Антропогенное изменение площади лесов ${{S}_{{for}}}\left( t \right)$ после 1960 г. нужно вычислять с учетом аффорестации (посадок), поэтому в формуле (6) вместо Fdef используется суммарный поток углерода за счет лесов Ffor, где Ffor =Fdef до 1960 г. Значения Ffor до 1990 г. включительно получены на основе данных из [29, 30].

Относительное изменение площади лесов $\frac{{S\left( t \right)}}{{{{S}_{0}}}}$ в момент времени t рассчитывается в модели как

(7)
$\frac{{S\left( t \right)}}{{{{S}_{0}}}} = 1 + \frac{{{{S}_{{for}}}\left( t \right)}}{{{{S}_{0}}}} + \frac{{{{S}_{T}}\left( t \right)}}{{{{S}_{0}}}},~$
где ${{S}_{{for}}}\left( t \right)$ – антропогенное изменение площади лесов, вычисляемое по формуле (6), ${{S}_{T}}\left( t \right)$ – прирост площади лесов в результате потепления, вычисляемый по формуле (2).

4.2. Сценарии изменения площади лесов и соответствующих потоков углерода в атмосферу за счет лесов до 2100 г.

• (1) Сценарий GEPL1997

В базовом сценарии из [13] предполагалось, что максимальное уменьшение площади тропических лесов составит примерно 40% (как и для умеренно-бореальных лесов) и будет достигнуто к 2030 г. Предполагалось, что после этого с десятилетней паузой начнется период восстановления тропических лесов до площади, примерно соответствующей 1990 г. Скорость увеличения площади умеренно-бореальных лесов за счет искусственного восстановления (посадок) для периода 1965–1993 гг. была оценена нами в 21.2 тыс. км2/год, и это же значение было использовано вплоть до 2100 г. Максимальная ожидаемая скорость восстановления тропических лесов была оценена по данным [31] и составила около 26 тыс. км2/год. Все потоки были пересчитаны с новым набором параметров модели (табл. 1). После коррекции коэффициента kw скорость прироста умеренно-бореальных лесов существенно увеличилась по сравнению с [13].

В соответствии с актуальным изменением площади лесов в мире по разным источникам, представленным в разделе 2 настоящей статьи, были рассчитаны средние потоки углерода в атмосферу за счет сведения и восстановления лесов для периода с 1960 г. до 2016 г. и построены, начиная с 2000 г., три сценария изменения площади лесов (2)–(4) на период до конца нынешнего столетия. Предварительно оценивался размер площади лесов, прирастаемых из-за потепления и сдвига границ экосистем.

• (2) Сценарий CONST

Прекращение изменений площадей лесов как умеренно-бореальных, так и тропических после 2010 г. Суммарный поток углерода в атмосферу без учета обратных связей равен 0.

• (3) Сценарий FAOSTAT

Линейная экстраполяция динамики изменения в 1990–2016 гг. площади бореальных лесов по данным FAOSTAT (2018): наблюдаемое восстановление умеренно-бореальных лесов со средней скоростью около 30 тыс. км2/год (полностью приходится на рост площади из-за потепления) и продолжение сведения тропических лесов со скоростью около 81 тыс. км2/год. Суммарный поток углерода в атмосферу без учета обратных связей равен 0.78 Гт C/год.

• (4) Сценарий LandSat

Линейная экстраполяция динамики изменения в 1990–2016 гг. площади бореальных лесов по данным о площади земной поверхности, покрытой деревьями сомкнутостью крон более 30% LandSat: сведение умеренно-бореальных лесов со средней скоростью около 93 тыс. км2/год и тропических лесов со средней скоростью около 92 тыс. км2/год. Суммарный поток углерода в атмосферу без учета обратных связей равен 1.65 Гт C/год.

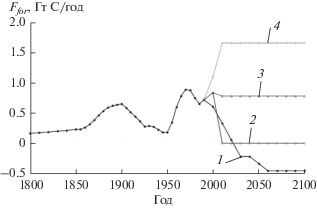
На рис. 3 представлен биотический поток Ffоr без учета обратных связей и его сценарии, составленные на основе описанных сценариев площадей лесов (1)–(4), различие в которых имеет место с 2000 г.

Рис. 3.

Биотический поток углерода в атмосферу за счет лесов Ffor: оценка до 1990 г. и различные сценарии его изменения с 2000 по 2100 г.: 1 – GEPL1997, 2 – CONST, 3 – FAOSTAT, 4 – LandSat (все без учета обратных связей).

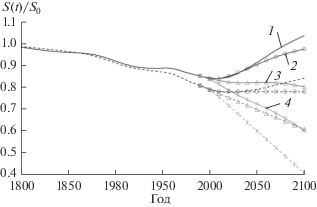
На рис. 4 представлена динамика относительного изменения площади лесов $\frac{{S\left( t \right)}}{{{{S}_{0}}}}$ по сценариям (1)–(4) с учетом и без учета прироста площади вследствие глобального потепления (три или два слагаемых из формулы (7)).

Рис. 4.

Динамика относительного изменения площадей лесов по сценариям (1)–(4): с учетом (сплошные линии) и без учета (пунктирные линии) прироста площади вследствие глобального потепления.

5. НЕТТО-ПОТОК УГЛЕРОДА В АТМОСФЕРУ

Нетто-поток углерода в атмосферу на выходе из биосферного блока есть ${{Q}_{b}} = {{F}_{{ba}}} - {{F}_{{ab}}}$, где Fab – это поток углерода из атмосферы в континентальную долгоживущую и короткоживущую биоту, Fba = F1+ F2, F1 – поток углерода в атмосферу из гумуса, подстилки и устойчивых соединений в почве, а

(8)
${{F}_{2}} = F_{{for}}^{{act}} + {{F}_{{soil}}},$
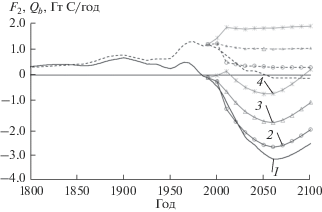
где $F_{{for}}^{{act}} = {{F}_{{for}}}\frac{{1 + \gamma {{\nu }_{a}}\left( {t - {{{{\tau }_{W}}} \mathord{\left/ {\vphantom {{{{\tau }_{W}}} 2}} \right. \kern-0em} 2}} \right)}}{{1 + \gamma {{\nu }_{a}}\left( {{{t}_{{1980}}}} \right)}}$ – поток углерода в атмосферу за счет лесов с учетом изменения биопродуктивности (поправочного множителя из формулы (4)), Fsoil – поток углерода в атмосферу за счет изменений в землепользовании [13].

На рис. 5 показаны потоки углерода в атмосферу F2 (пунктирные линии) и нетто-потоки из биосферы в атмосферу Qb (сплошные линии). Основные изменения в биосферном резервуаре в период до 1900-х годов связаны с прямым антропогенным воздействием – вырубкой лесов и возделыванием земель, поэтому потоки F2 и Qb близки по значениям. После 1950 г. в условиях повышения концентрации CO2 и роста среднеглобальной температуры расчетный поток углерода Fab из атмосферы в континентальную долгоживущую и короткоживущую биоту увеличивается в результате повышения биопродуктивности растений и сдвига границ экосистем. К середине XXI-го столетия прогнозируемые темпы возрастания глобальной температуры и атмосферной концентрации CO2 снижаются, поэтому разница между абсолютными значениями потоков Fab и Fba начинает уменьшаться. Это сопровождается прохождением выраженного минимума нетто-потока Qb (максимума стока) примерно около 2050–2060 гг. для всех без исключения сценариев изменения площадей лесов. Глубина этого минимума зависит от уровня дефорестации в рамках конкретного сценария. Для наиболее драматического сценария (4), предполагающего значительное сведение как бореальных, так и тропических лесов, абсолютное значение этого минимума невелико (максимальный сток не превышает 1 ГтС/год), поэтому к 2100 г. Fba уже превышает Fab по абсолютному значению, и биосфера снова превращается в источник дополнительного углерода в атмосферу (Qb переходит через 0). Для сценария (3) нетто-поток Qb к 2100 г. возвращается примерно к современным значениям, но имеет противоположную по знаку скорость изменения. Сценарии (1) и (2) показывают заметное замедление стока атмосферного углерода в биосферу, остающегося тем не менее на значительном уровне.

Рис. 5.

Потоки углерода за счет лесов и изменений в землепользовании с учетом изменения биопродуктивности F2 (пунктирные линии) и нетто-потоки углерода Qb из биосферы в атмосферу (сплошные линии) с 2000 г. по сценариям (1)–(4).

6. ЗАКЛЮЧЕНИЕ

Как отмечалось в [12, 13], превращение биосферы из источника в сток избыточного углерода из атмосферы, начавшееся в конце прошлого столетия, приводит к существенному смягчению антропогенного давления на окружающую среду. Однако скорость изменения стока углерода в наземную биоту будет снижаться и к середине текущего столетия по нашим расчетам достигнет нуля, а затем сток начнет уменьшаться. Расчеты по сценарию LandSat, предполагающему значительное сведение как бореальных, так и тропических лесов, показывают изменение направления нетто-потока атмосфера–биосфера (переход через 0) уже в конце текущего столетия – следовательно, биосфера опять может превратиться в источник дополнительного углерода в атмосфере. Сценарий FAOSTAT, описывающий восстановление умеренно-бореальных лесов и продолжающееся интенсивное сведение тропических лесов, приводит в 2100 г. к возвращению нетто-потока на современный уровень. В наиболее благоприятных для судьбы лесов сценариях GEPL1997 и CONST биосфера вплоть до конца нынешнего столетия остается эффективным стоком углерода, препятствующим росту концентрации СО2 в атмосфере. Максимальное различие нетто–потоков углерода из биосферы в атмосферу для всех рассмотренных сценариев составляет почти 2.5 Гт C/год и приходится примерно на середину текущего столетия.

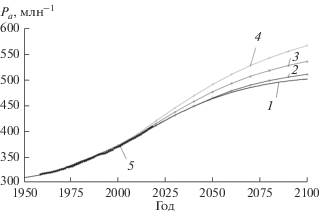
Соответствующее этим сценариям расчетное изменение атмосферной концентрации CO2Pa показано на рис. 6. Разница между значениями концентрации CO2 для рассмотренных сценариев изменения площади лесов монотонно возрастает, достигая к 2100 г. 65 млн–1. Реализация любого, кроме (1), сценария ведет к опасному повышению концентрации CO2 и невозможности удержания среднеглобальной температуры в пределах 2 градусов.

Рис. 6.

Расчетная атмосферная концентрация CO2 по сценариям (1)–(4) и фактические данные (5) со станции Мауна Лоа [15, 32, 33].

Список литературы

  1. Houghton R.A., Nassikas A.A. Global and fluxes of carbon from land use and land cover change 1850–2015 // Global Biogeochem Cy. 2017. V. 31. P. 456–472.

  2. Climate Change 2013: The Physical Science Basis / Eds: Stocker T.F., Qin D., Plattner G.-K. Cambridge, UK and New York, USA: Cambridge University Press, 2013. 1552 p.

  3. Елисеев А.В. Глобальный цикл CO2: основные процессы и взаимодействие с климатом // Фундаментальная и прикладная климатология. 2017. Т. 4. С. 9–31.

  4. Елисеев А.В. Оценка изменения характеристик климата и углеродного цикла в XXI веке с учетом неопределeнности значений параметров наземной биоты // Изв. РАН. Физика атмосферы и океана. 2011. Т. 47. № 2. С. 147–170.

  5. Тарко А.М., Усатюк В.В. Моделирование глобального биогеохимического цикла углерода с учетом сезонной динамики и анализ динамики концентрации CO2 в атмосфере // Докл. РАН. 2013. Т. 448. № 6. С. 711–714.

  6. Peng J., Dan L. Impacts of CO2 concentration and climate change on the terrestrial carbon flux using six global climate–carbon coupled models // Ecol Model. 2015. V. 304. P. 69–83.

  7. Prăvălie R. Major perturbations in the Earth’s forest ecosystems. Possible implications for global warming // Earth-Sci Rev. 2018. V. 185. P. 544–571.

  8. Birdsey R., Pan Y. Trends in management of the world’s forests and impacts on carbon stocks // Forest Ecol Manag. 2015. V. 355. P. 83–90.

  9. Определяемый на национальном уровне вклад (INDC) Российской Федерации с пояснениями. https://www4.unfccc.int/sites/submissions/INDC/ Published%20Documents/Russia/1/Russian%20Submission%20INDC_rus.doc

  10. Yan Y. Integrate carbon dynamic models in analyzing carbon sequestration impact of forest biomass harvest // Sci Total Environ. 2018. V. 615. P. 581–587.

  11. Nakayama T., Pelletier G.J. Impact of global major reservoirs on carbon cycle changes by using an advanced eco-hydrologic and biogeochemical coupling model // Ecol Model. 2018. V. 387. P. 172–186.

  12. Klimenko A.V., Klimenko V.V., Fyodorov M.V., Snytin S.Yu. Modification of major CO2 sources under conditions of the man-changed environment // Proc. of the 5th Int. Conf. Energex’93. Seoul. 1993. V. 5. P. 56–61.

  13. Клименко В.В., Клименко А.В., Андрейченко Т.Н. и др. Энергия, природа и климат. M.: Изд-во МЭИ, 1997. 218 с.

  14. Klimenko V.V., Tereshin A.G., Mikushina O.V. Do we really need a carbon tax? // Appl Energ. 1999. V. 64. № 1–4. P. 311–316.

  15. Tans P.Keeling R.Global Greenhouse Gas Reference Network. SIO and NOAA/ESRL. 2019. www.esrl. noaa.gov/gmd/ccgg/trends/

  16. Marcott S.A., Shakun J.D., Clark P.U., Mix A.C. A reconstruction of regional and global temperature for the past 11300 years // Science. 2013. V. 339. № 6124. P. 1198–1201.

  17. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment. Report of the Intergovernmental Panel on Climate Change / Eds: Solomon S., Qin D., Manning M. Cambridge, UK and New York, USA: Cambridge University Press, 2007. 996 pp.

  18. FAO Production Yearbook 1994. V. 48. FAO. Rome. 1995. 243 p.

  19. FAOSTAT. FAO food and agriculture database. http:// www.fao.org/faostat/en/#data

  20. Global Forest Resources Assessment 2015. Rome: FAO, 2015. 252 p.

  21. Keenan R.J., Reams G.A., Achard F. et al. Dynamics of global forest area: Results from the FAO Global Forest Resources Assessment 2015 // Forest Ecol Manag. 2015. V. 352. P. 9–20.

  22. Anderson J.R., Hardy E.E., Roach J.T., Witner R.E. A land use land cover classification system for use with remote sensing data. Geological Survey Professional Paper 964. Washington, D.C.: U.S. Government Printing Office, 1976. 28 p.

  23. Justice C.O., Townshend J.R.G., Holben B.N., Tucker C.J. Analysis of the phenology of global vegetation using meteorological satellite data // Int J Remote Sens. 1985. V. 6. № 8. P. 1272–1318.

  24. Issues in the Integration of Research and Operational Satellite Systems for Climate Research: Part I. Science and Design. National Research Council. Washington, D.C.: National Academy Press, 2000. 152 p.

  25. Friedl M.A., Sulla–Menashe D., Tan B. et al. MODIS Collection 5 global landcover: Algorithm refinements and characterization of new datasets // Remote Sens Environ. 2010. V. 114. № 1. P. 168–182.

  26. Li W., MacBean N, Ciais P. et al. Gross and net land cover changes in the main plant functional types derived from the annual ESA CCI land cover maps (1992–2015) // Earth Syst. Sci. Data. 2018. V. 10. № 1. P. 219–234.

  27. Curtis P.G., Slay C.M., Harris N.L. et al. Classifying drivers of global forest loss // Science. 2018. V. 361. № 6407. P. 1108–1111.

  28. Hansen M.C., Potapov P.V., Moore R. et al. High-resolution global maps of 21st-century forest cover change // Science. 2013. V. 342. № 6160. P. 850–853.

  29. Houghton R.A., Skole D.L. Changes in the global carbon cycle between 1700 and 1985 // The Earth Transformed by Human Action / Ed: Turner B.L., Clark W.C., Kates R.W. et al. Cambridge University Press, 1990. P. 393–408.

  30. Woodwell G.M., Hobbie J.E., Houghton R.A. et al. Global deforestation: contributions to atmospheric carbon dioxide // Science. 1983. V. 222. P. 181–186.

  31. Climate Change. 1992. The Supplementary Report to the IPCC Scientific Assessment / Eds: Houghton J.T., Callander B.A., Varney S.K. Cambridge University Press, 1992. 216 p.

  32. Keeling C.D., Bacastow R.B., Bainbridge A.E. et al. Atmospheric carbon dioxide variations at Mauna Loa Observatory, Hawaii // Tellus. 1976. V. 28. P. 538–551.

  33. Thoning K.W., Tans P.P., Komhyr W.D. Atmospheric carbon dioxide at Mauna Loa Observatory 2. Analysis of the NOAA GMCC data, 1974–1985 // J Geophys Res. 1989. V. 94. P. 8549–8565.

  34. Siegenthaler U. Uptake of excess CO2 by an outcrop-diffusion model of the ocean // J Geophys Res. 1983. V. 88. № C6. P. 3599–3608.

  35. Emanuel R.E., Killough G.G., Post W.M., Shugart H.H. Modeling terrestrial ecosystems in the global carbon cycle with shifts in carbon storage capacity by land-use change // Ecology. 1984. V. 65. P. 970–983.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал